基于阻抗法的懸掛器試壓波動抑制技術

劉 均 ， 袁 峰

(1.東北石油大學電氣信息工程學院 大慶, 163318) (2.哈爾濱工業大學電氣工程與自動化學院 哈爾濱, 150001)

?

基于阻抗法的懸掛器試壓波動抑制技術

劉 均1,2， 袁 峰2

(1.東北石油大學電氣信息工程學院 大慶, 163318) (2.哈爾濱工業大學電氣工程與自動化學院 哈爾濱, 150001)

以水擊方程為基礎，借鑒電路的阻抗分析方法，研究連續波動在管道中的傳遞特性。分析了外接管道對波動傳遞的影響，設計了用于濾除管道內特定頻率波動的濾波器，推導出管道長度和濾波器尺寸與波動傳遞之間關系。通過實際應用發現，以阻抗理論為基礎設計的濾波器能夠很好地抑制泵壓波動，提高試壓過程的準確性和效率。

連續波動； 試壓； 濾波器； 懸掛器

引 言

懸掛器是在固井過程中將尾管與上層套管聯接起來的一種機械裝置，用于將尾管座掛在上層套管的末端[1]。懸掛器懸掛動作的觸發是由懸掛器內缸的壓力決定的。當進行懸掛操作時，在地面注入鉆井液進行蹩壓，當鉆井液壓力增至額定壓力時，剪斷液壓缸銷釘，讓懸掛器的內缸和外缸產生相對位移，從而帶動卡瓦漲開，完成尾管的座掛[2-4]。為了讓懸掛器正常工作，在懸掛器生產過程中需要通過試壓技術確定懸掛器的工作壓力。試壓使用的試壓泵一般為電動往復式柱塞泵，由電機驅動柱塞，帶動滑塊運動，將流體注入懸掛器液缸，當液缸銷釘斷裂時的壓力就是懸掛器的工作壓力。在試壓過程中，由于試壓泵的轉速比較高，如果直接用管道將試壓泵和液缸連接起來，由于柱塞的運動，在管道和液缸中會產生劇烈的壓力波動，從而導致同樣材質與尺寸的銷釘測試結果相差很大。分析認為，這個誤差是由壓力劇烈變化造成的，因此為了減少測試時的誤差，需要對管道和液缸內的壓力波動進行抑制。

目前，國內外對于管道內壓力波動的研究主要集中在水擊波在管道中的傳遞和振蕩過程，研究的是管道中壓力突然改變后，壓力脈沖的傳遞與衰減特性[5-11]。管道中連續波動的分析與計算主要集中在能量的分布和對振動信號的采集處理[12-13]。一般認為，管道對于波動信號類似于低通濾波器，低頻信號衰減少，高頻信號衰減多，但對如何抑制管道中特定頻率的波動理論和方法較少涉及[14-18]。

筆者以水擊方程為出發點，研究連續波動在管道內的傳遞機理，推導了利用傳遞矩陣描述管道內壓力波的數學模型。基于傳遞矩陣設計了用于抑制壓力波動的濾波器，解決了銷釘剪切壓力高速測量的問題。

1 管道內壓力波動的矩陣模型

管道內單個壓力波的傳遞可以用水擊方程表示，該方程描述了當管道中閥門關閉后，管道中產生的單個壓力波動在管道中的傳遞情況[16]。

(1)

其中：H為水頭；V為流速，D為等效水力直徑；β為管道與水平面的夾角；a為波速；f為與摩擦力相關的系數。

式(1)為典型的非線性雙曲型偏微分方程組，有很多經典解法，但都為數值解。對于研究管道的頻率響應特性，只有數值解是不夠的。

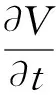
(2)

其中：A為管道等效水力面積。

如果認為摩擦力的影響f不隨時間和位置改變，將式(2)中的第1式對x求導，第2式對t求導后推出

(3)

其中：R=fQ/2gDA2為一常數。

如果管路一端試壓泵運轉時加載在管道中的壓力波動形式為正弦波，則可求出式(3)的解為

(4)

其中：c1，c2為常數，與邊界條件相關；ω為角頻率；γ2=-(ω2+jAgωR)/a2；p(x)為壓力波動的幅值。

由于a，A，R對于具體的管道可以認為是常量，那么γ只與角頻率ω相關。將式(4)及其導數帶入式(2)，可以求出

(5)

其中：q(x)為流量波動的幅值。

p(x)和q(x)為距離x的函數。對于具體的管道，γ只與角頻率ω相關，可以將γ定義為管道流體傳播常數。由于水壓驅動了水分子的運動，電壓是電子流動的動力，二者具有相似性，故可以模仿電路理論中阻抗的定義方式來定義管道對流體壓力波動的阻抗為

(6)

Z(x)代表了管道對波動的阻力，在輸電理論中，定義無限長輸電線路的阻抗為特征阻抗，在管道中也可以定義管道的特征阻抗為Zc=ja2γ/gAω，它的物理含義是無限長管道對波動的阻力[19]。

對于長度為l的管道，如果知道了波動起始位置x=0處的壓力振幅pi=p(0)和流量振幅qi=q(0)，根據式(4)和式(5)，就可以計算出c1和c2

可以將任意位置x處的壓力振幅和流量振幅表示為

末端x=l處的壓力振幅po可表示為

pisinh(γl)-Zcqicosh(γl)

(7)

同樣，將末端x=l處的流量振幅qo表示為

(8)

將式(7)，(8)寫成矩陣方式

(9)

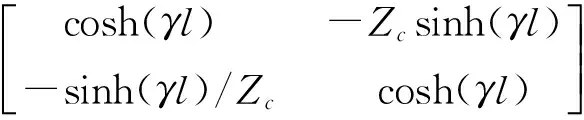
當有不同管道串聯時，在聯接點處相當于一條管道的末端和另一條管道的始端相連，且聯接點處壓力振幅和流量振幅相等，因此聯接點的方程為

連接點的傳遞矩陣為

(10)

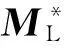
(11)

其中：ML1為第1條管道的傳遞矩陣；ML2為第2條管道的傳遞矩陣。

根據傳遞矩陣可以寫出管道終端處壓力振幅po和流量振幅qo與始端處壓力振幅pi和流量振幅qi的關系

(12)

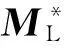
(13)

式(13)說明在負載確定的情況下，波動經過串聯異徑管道后振幅的變化情況。

2 管道的幅值頻率特性

由于式(13)得到的是波動在管道入口和出口的幅值之比，說明了管道對波動的衰減情況。如果固定除波動的角頻率ω(ω=2πf)之外的參數，可以繪制出管道對不同頻率信號的響應曲線。對于長度分別為50m和200m的兩根管道，如果取直徑D=40mm，波速a=1 280 m，終端阻抗R0=3Zc，依據式(9)和式(13)計算出這兩條管道的幅值頻率特性曲線，如圖1所示。可以看出，不同頻率的信號通過管道后其衰減幅度是不一樣的。當輸入端波動信號的幅值pi一定時，輸出端波動信號的幅值po隨著信號頻率的增加而呈現波動衰減，特別在低頻部分會出現po遠大于pi的情況，這是由于波動傳遞過程中的反射與疊加造成的。

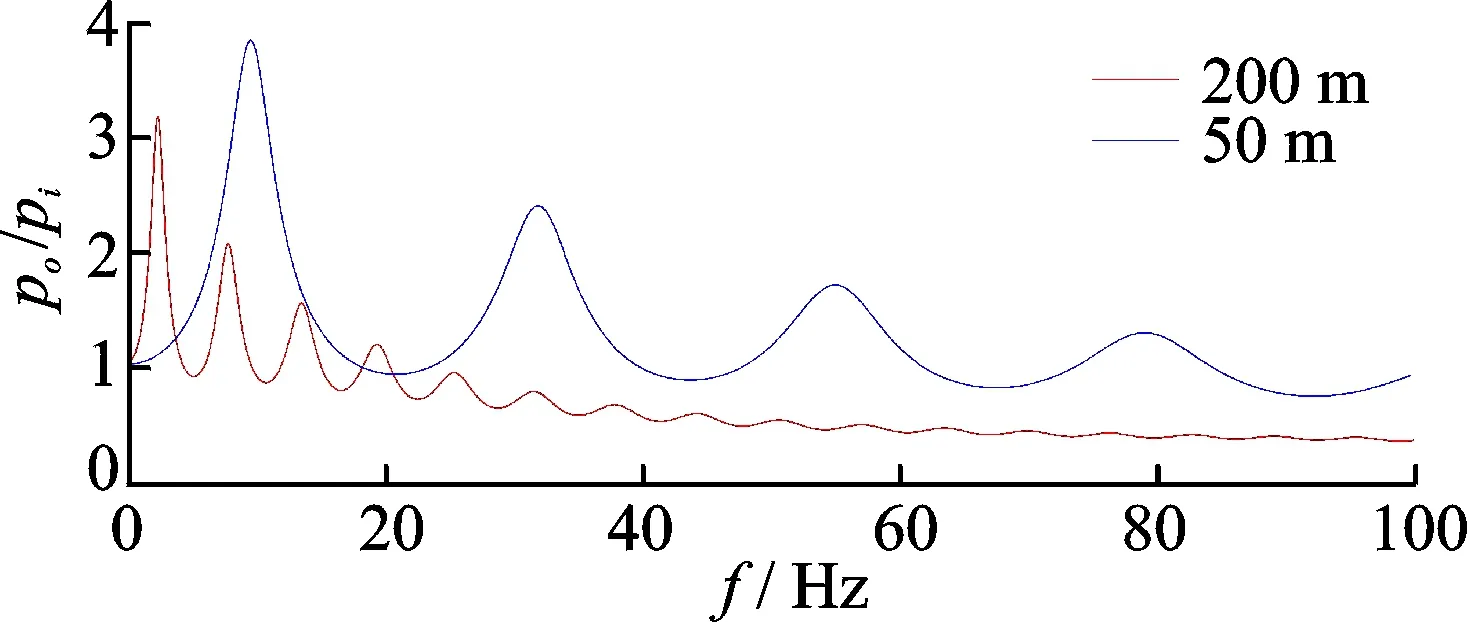
圖1 管道的幅值頻率響應Fig.1 The amplitude frequency characteristic in pipeline

對于50m短管道來說，輸入端的波動會完整地傳遞到輸出端，衰減很小，在某些頻段還會出現輸出波動大于輸入波動的情況，正是這種波動導致了測試誤差。對于較長的管道，波動主要集中在低頻區域，隨著頻率的上升，末端振幅的波動現象減少。

3 用于抑制管道中波動的濾波器

為了抑制管道中的波動，設計合適的管道結構用于改變管道的頻率幅值特性，使試壓泵工作時產生的波動信號衰減掉。由于泵工作時轉速是一定的，設計的濾波器只需要濾除特定頻率的信號即可。

管道的物理參數會影響波動的傳遞，設計如圖2所示的管道結構。將傳遞壓力的管道分為兩段L1和L2，在L1和L2的連接部位安裝一個儲液罐L4，儲液罐L4通過短管L3與L1和L2相連，儲液罐L4為一圓柱形容器。設L1，L2，L3和L4的長度分別為l1，l2，l3和l4；L1，L2和L3的截面積均為A，L4的截面積A4遠大于A。L1左端為波動輸入端，輸入的壓力振幅為pi，流量振幅為qi；L2的右端為波動輸出端，輸出的壓力振幅為po，流量振幅為qo；在L1，L2和L3的連接點P處，壓力分別為p1，p2，p3，流量振幅分別為q1，q2，q3；在L4末端壓力振幅為pm，流量振幅為qm。

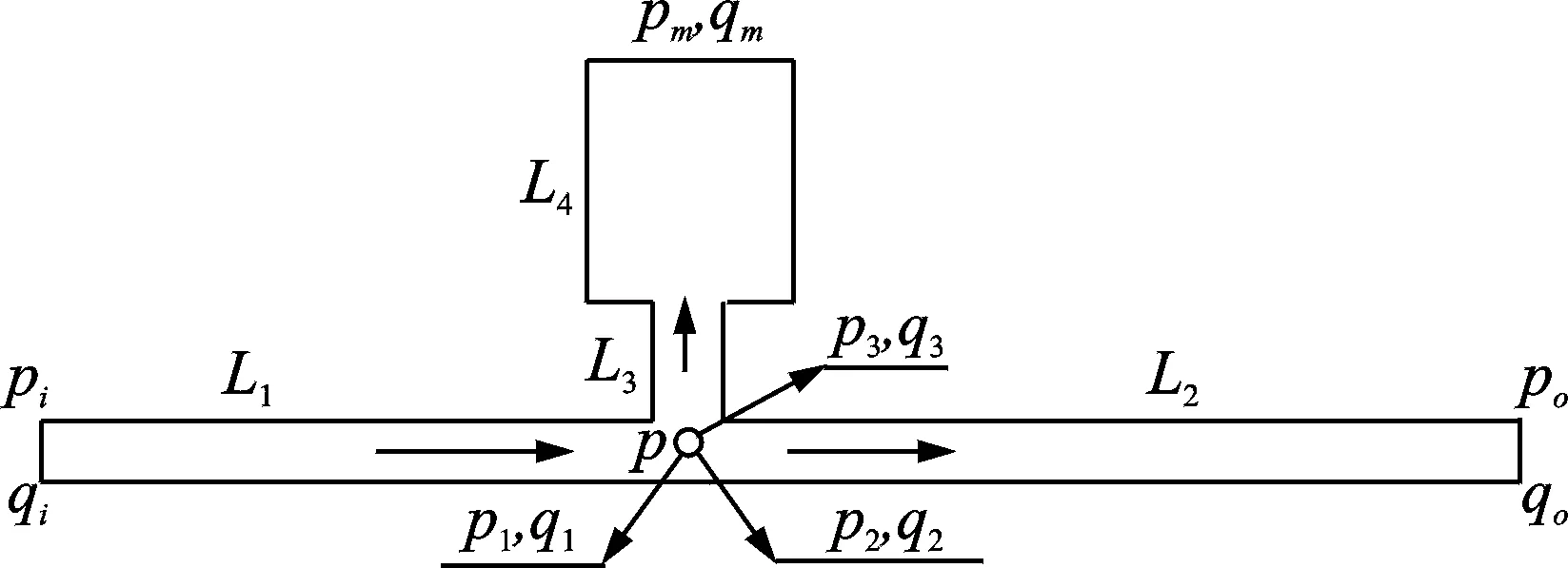
圖2 濾波器結構圖Fig.2 Structure of the filter

由于在連接點P處壓力連續，p1=p2=p3，q1=q2+q3，因此連接點處傳遞矩陣可以表示為

(14)

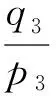
L3和L4串聯后的矩陣傳遞表達式為

其中：pm和qm為L4末端的壓力與流量振幅。

由于L4末端封閉，則qm=0，可以推導出(CL3AL4+DL3CL4)p3+(CL3BL4+DL3DL4)q3=0，最后計算出

(15)

由于L3較短，且處于L3和L4中的流體基本不流動，忽略分支管以及容器中的摩擦力，可以將傳遞系數和特征阻抗簡化為γ=jω/a，Zc3=ρa/A3，Zc4=ρa/A4。根據雙曲函數和三角函數的關系，將thγl簡化為

從而得到

(16)

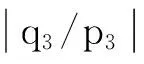
(17)

計算出L1左端的壓力和流量波動與L2右端的壓力和流量波動的關系為

(18)

根據式(13)和式(18)，得到帶濾波器管道的幅值與頻率的衰減特性。假設波速a為1 280m/s；L1，L2和L3具有相同的直徑為20mm，長度分別為0.49，15.5和0.2m；容器L4的直徑為200mm，長度l4為292mm。圖3為此時管道的幅值頻率特性。可以看出，加入濾波器后，管道的頻率幅值特性與圖1相比發生了改變。在30～60Hz和65～100Hz之間的振蕩得到了較好抑制，但在某些頻段振蕩會加強，出現共振現象。例如，在60～65Hz之間振蕩非常劇烈，此頻率范圍是整個管道的共振范圍，需要避免使用此頻率，否則會導致管道的損壞。根據參數計算出串聯管道的諧振頻率ωn為529 r/min，即84Hz。圖3中，84Hz信號衰減是最大的，在諧振頻率附近的信號也有很大衰減，可以利用濾波器的特性完成對泵壓波動的濾除。

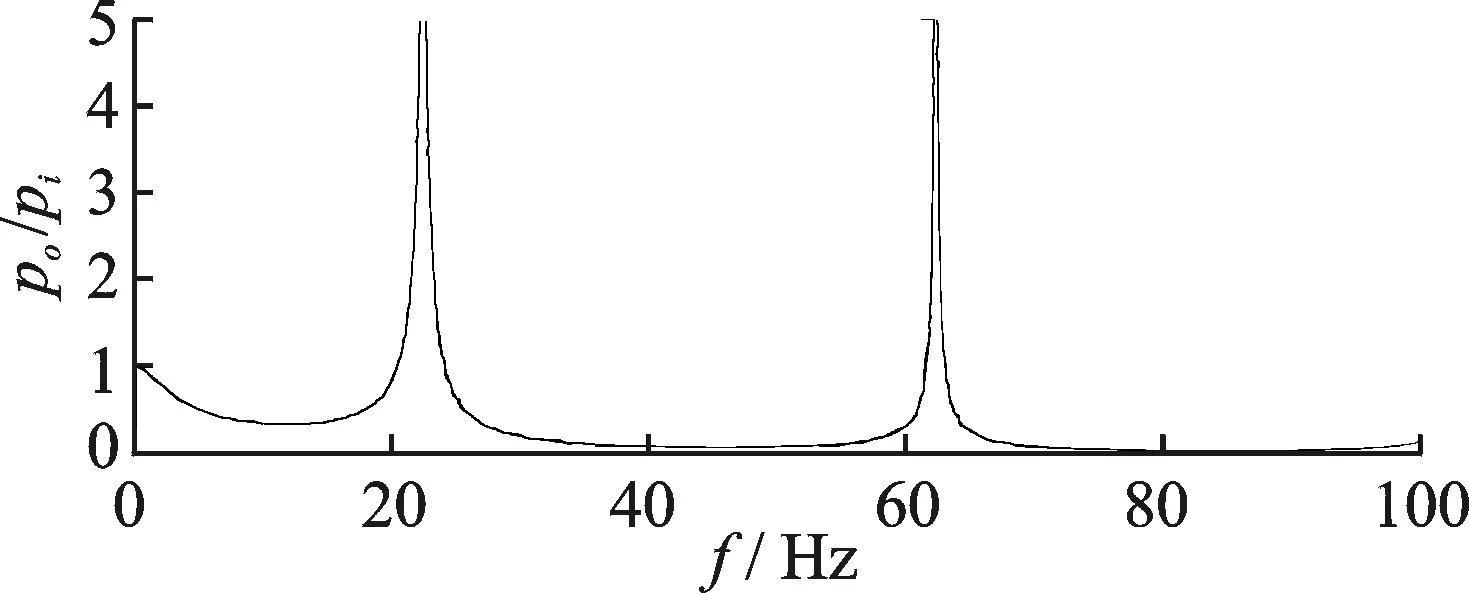
圖3 帶濾波器管道的幅值頻率特性Fig.3 The amplitude frequency characteristics for the pipeline with filter

4 實驗與應用

為了解決高速試壓的需要，設計制作了用于測試懸掛器工作壓力的測試裝置，如圖4所示。

圖4 懸掛器試壓裝置Fig.4 The hanger pressure test device

測試裝置由橫放的懸掛器雙層液缸、直徑為20mm的快接管道、水泵、壓力傳感器和計算機系統組成。雙層液缸分為內缸和外缸，內外缸通過銷釘固定并密封。傳感器測量范圍在25MPa，精度為0.1%，采樣頻率為500Hz。在試壓過程中，首先加工4只同尺寸銷釘，取其中兩只銷釘安裝到液缸上，然后對管道和液壓缸注水并排氣，由試壓泵加壓，缸內壓力逐漸上升，直至銷釘剪斷為止。壓力傳感器記錄銷釘在斷裂瞬間的壓力值，這個值用于標記剩余兩支銷釘的剪切壓力值，這個壓力值就是懸掛器出廠后的觸發壓力值。

在測試裝置中使用3柱塞泵，電機轉速為950r/min，電機每旋轉一周產生3個壓力脈沖。管道內壓力波動頻率大約在48Hz左右，在不使用濾波器，直接將泵的輸出通過管道接入液缸時，管道和懸掛器內的壓力波動很劇烈，給測試過程帶來很大誤差，測試時的壓力波形如圖5所示。對于同批次加工的同型號銷釘，多次測量的結果相差很大，從測量的壓力曲線來看，銷釘斷裂的瞬間，壓力值可以出現在波峰和波谷之間的任意位置。對同批次銷釘進行多次測試，計算測試結果的平均值，用參與計算的單次測量值與平均值比較可以發現，單次測量值都偏離平均值，最大測量值和最小測量值之差超過1MPa，且多次測量的結果沒有規律性，故可以認為測量誤差很大，數據不可信。

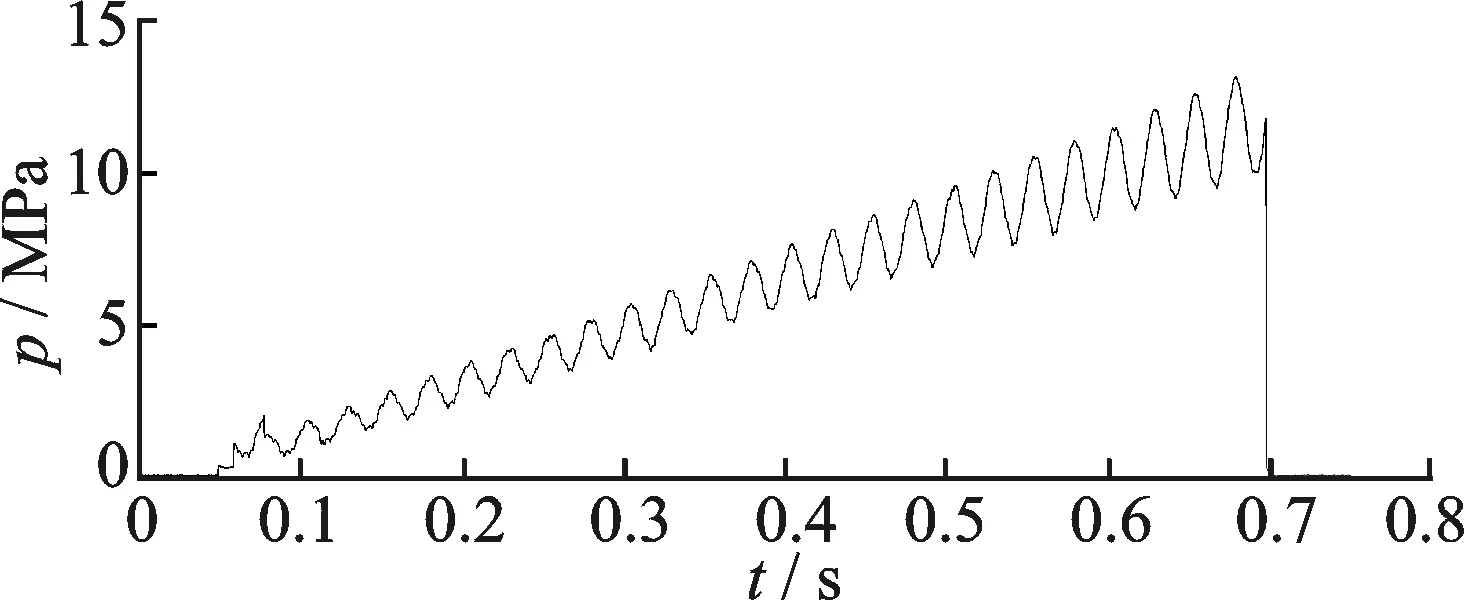
圖5 不使用濾波器時懸掛器內壓力變化Fig.5 Pressure changes in the hanger without filter

在距離試壓泵0.5m處加入直徑為200mm，長度為292mm的濾波器后，壓力傳感器測量到的管道中壓力波動如圖6所示。可以看出，管道中壓力波動明顯減小，壓力的上升比較平緩，同批次銷釘多次測量后的最大測量值與最小測量值之差小于0.2MPa，這個誤差處于可接受的范圍，因此認為濾波器能有效濾除泵壓的波動，解決了銷釘剪切壓力高速測量的問題。

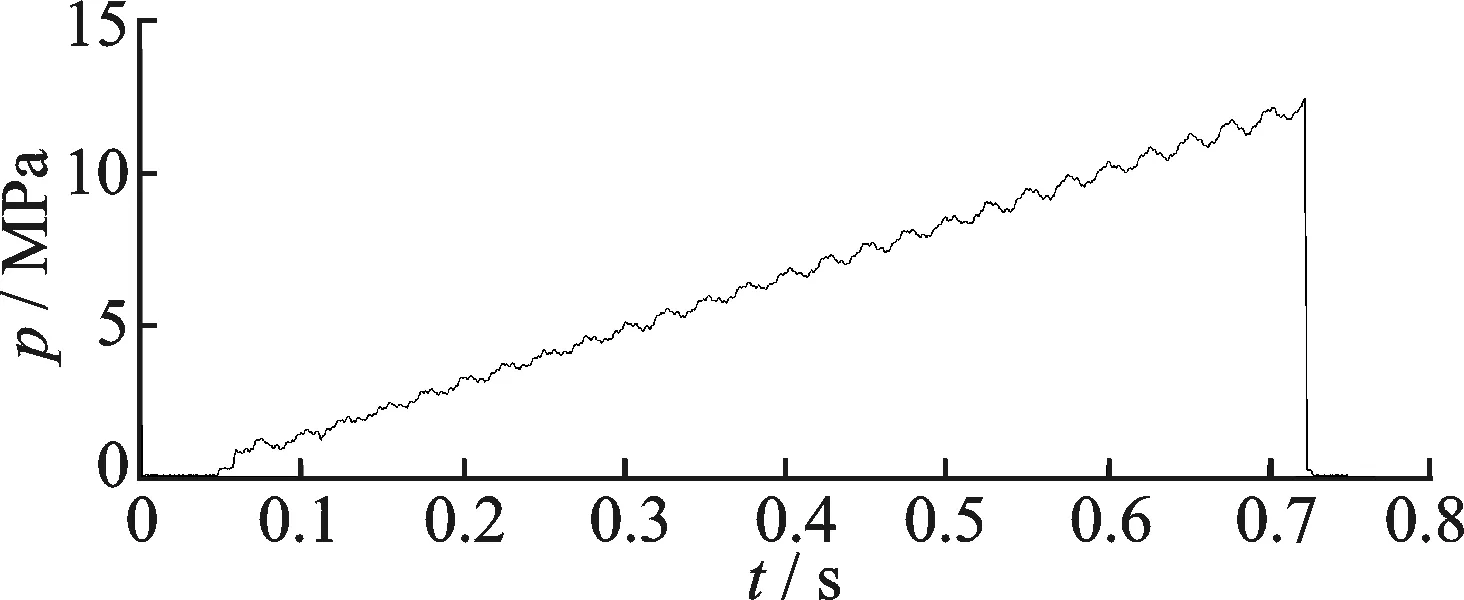
圖6 使用濾波器后管道內壓力變化Fig.6 Pressure changes in the hanger with filter

不同速度的泵由于轉速不同，在管道內產生的波動信號頻率也不同，需要根據具體的信號頻率設計濾波器的尺寸。另外，在實驗中要注意濾波器中的空氣。當濾波器容器中混入空氣時，由于空氣有很高的壓縮比，會改變濾波器的諧振頻率，導致濾波性能不好。最好的解決辦法是將濾波器處于管道下方，讓濾波器內部的空氣自然排出。

5 結 論

1) 利用阻抗法描述連續壓力波動在管道中的傳遞情況，可以將管道材質和流體特性等因素用阻抗和傳遞系數簡單地表示出來。

2) 用矩陣模型描述連續波動信號在管道中的傳遞特性，適用于分析各種復雜結構管道中連續波動的傳遞。

3) 在直管道中，當連續的壓力波動產生后，不同頻率的信號傳遞距離是不一樣的。隨著頻率的增加，管道出口處壓力振幅呈現周期性衰減，總體趨勢為低頻衰減小，高頻衰減大。

4) 在管道中安裝濾波器后，濾波器改變了管道的頻率響應，適當的設計能有效減少管道中的壓力波動。不同形狀的濾波器會帶來不同的頻率響應特性，本研究涉及的模型適用于圓柱體濾波器，其他形狀濾波器的濾波特性需要進一步研究。

[1] 馬開華, 朱德武, 馬蘭榮. 國外深井尾管懸掛器技術研究新進展[J]. 石油鉆探技術, 2005, 33(5): 52-55.

Ma Kaihua, Zhu Dewu, Ma Lanrong. Advances in liner hanger techniques in deep wells outside China[J]. Petroleum Drilling Techniques, 2005, 33(5): 52-55. (in Chinese)

[2] Lohoefer C L, Mathis B, Brisco D. Expandable liner hanger provides cost-effective alternative solution[C]∥IADC/SPE Drilling Conference. New Orleans, Louisiana: Society of Petroleum Engineers, 2000:1-12.

[3] Nida R, Meijs R, Reedd S. Innovative expandable liner-hanger application saves time on pinedale anticline drilling operations: two case studies[C]∥SPE Annual Technical Conference and Exhibition. Houston,Texas: Society of Petroleum Engineers, 2004:1-8.

[4] 吳柳根, 馬建忠, 寧學濤. 膨脹懸掛器技術在石油工程中的應用[J]. 石油礦場機械, 2012, 41(9): 59-63.

Wu Liugen, Ma Jianzhong, Ning Xuetao. Expandable liner hanger technology applied in petoleum engineering[J]. Oil Field Equipment, 2012, 41(9): 59-63. (in Chinese)

[5] 胡榮霞, 李金海. 泵系統中水錘與閥控制的研究綜述[J]. 水利科技與經濟, 2006, 12(12): 816-818.

Hu Rongxia, Li Jinhai. Research review of water hammer and valve control in pump systems[J]. Water Conservancy Science and Technology and Economy, 2006, 12(12): 816-818. (in Chinese)

[6] 曹慧哲, 賀志宏, 何鐘怡. 有壓管道水擊波動過程及優化控制的解析研究[J]. 工程力學, 2008, 25(6): 22-26.

Cao Huizhe, He Zhihong, He Zhongyi. The analytic research on the wave process and optimal control of water hammer in pipes[J]. Eegineering Mechanics, 2008, 25(6): 22-26.(in Chinese)

[7] Ghidaoui M S, Zhao Ming, McInnis D A. A review of water hammer theory and practice[J]. Applied Mechanics Reviews, ASME, 2005, 58(1): 49-76.

[8] Wang Jianxun, Liu Huijin. A time-frequency mixed method for on-line monitoring of harmonics and interharmonics[C]∥2011 International Conference on Advanced Power System Automation and Protection. Beijing: IEEE, 2011: 228-233.

[9] Liu Ronghui, Yang Erbin, Yang Xiu. Analysis of transient harmonics in power systems based on wavelet packet transform[C]∥The 3rd International Conference on Power Electronics and Intelligent Transportation System. Shenzhen: International Institute of Tropical Agriculture Association, 2011: 345-348.

[10]Jameson A. Time dependent calculations using multigrid, with applications to unsteady flow past airfoils and wings[J]. AIAA Journal, 1991, 6: 1591-1596.

[11]Boucher R F, Kitsiors E E. Simulation of fluid network dynamics by transmission line modeling[J]. Joumal of Mechanical Engineering Science, 1986, 92(3): 97-111.

[12]朱顯明, 張國良, 黃其柏, 等. 均勻流管自由振動的能量分布特征[J]. 振動、測試與診斷, 1999, 19(2): 98-100.

Zhu Xianming, Zhang Guoliang, Huang Qibai, et al.Characteristics of free vibration energy distribution in a pipe filled with uniformly flowing fluid[J]. Journal of Vibration, Measurtment & Diagnosis, 1999, 19(2): 98-100. (in Chinese)

[13]谷立臣, 閆小樂, 劉澤華. 小波變換的流體壓力信號自適應濾波方法研究[J]. 振動、測試與診斷, 2009, 29(2): 205-208.

Gu Lichen, Yan Xiaole, Liu Zehua. Adaptive filtering method for fluid pressure by using wavelet transform[J]. Journal of Vibration, Measurtment & Diagnosis, 2009, 29(2): 205-208.(in Chinese)

[14]劉修善, 蘇義腦. 鉆井液脈沖信號的傳輸特性分析[J]. 石油鉆采工藝, 2000, 22(4): 8-10.

Liu Xiushan, Su Yinao. Investigation on the transmission behaviors of drilling fluid pulse signal[J]. Oil Drilling & Production Technology, 2000, 22(4): 8-10.(in Chinese)

[15]Klotz C, Kaniappan A, Thorsen A K. A new mud pulse telemetry systems reduce risks when drilling complex extended reach well[C]∥IADC/SPE Asia Pacific Drilling Technology Conference and Exhibition. Jakarta, Indonesia: Society of Petroleum Engineers, 2008:1-12.

[16]何樹山, 劉修善. 鉆井液正脈沖信號的衰減分析[J].鉆采工藝, 2001, 24(6):1-12.

He Shushan, Liu Xiushan. Analysis of signal attenuation for positive drilling fluid pulse[J]. Drilling & Production Technology, 2001, 24(6): 1-12. (in Chinese)

[17]Klotz C, Bond P, Wasserman I, et al. A new mud pulse telemetry system for enhanced MWD/LWD application[C]∥IADC/SPE Drilling Conference. Orlando, Florida: Society of Petroleum Engineers, 2008:1-5.

[18]王翔, 王瑞和, 紀國棟. 井筒內鉆井液連續脈沖信號傳輸頻率相關摩阻模型[J]. 石油學報, 2009, 30(3): 445-449.

Wang Xiang, Wang Ruihe, Ji Guodong. Frequency dependent friction model for consecutive pulse signal of drilling fluid transmitting in borehole[J]. Acta Petrolei Sinica, 2009, 30(3): 445-449.(in Chinese)

[19]羅志昌. 流體網絡理論[M]. 北京：機械工業出版社, 1988: 14-23.

10.16450/j.cnki.issn.1004-6801.2016.04.011

國家自然科學基金資助項目(61004067)

2014-07-30；

2014-10-10

TE937；TH812

劉均，男，1976年8月生，副教授。主要研究方向為井下儀器與裝置的研發。曾發表《鉆柱內連續波信號傳輸模型與幅頻特性研究》(《儀器儀表學報》2015年第1期)等論文。

E-mail: dragon2k@163.com