拋體運動與圓周運動命題規律探究

山東省棗莊二中　朱懷東

拋體運動與圓周運動命題規律探究

山東省棗莊二中朱懷東

一、運動的合成與分解

該熱點在高考中主要以選擇題的形式進行考查，命題角度有以下幾點：（1）根據分運動性質判斷合運動性質。（2）根據合運動性質判斷分運動性質。（3）考查運動中的臨界極值問題。

例1（2014年四川卷）有一條兩岸平直、河水均勻流動、流速恒為v的大河。小明駕著小船渡河，去程時船頭指向始終與河岸垂直，回程時行駛路線與河岸垂直。去程與回程所用時間的比值為k，船在靜水中的速度大小相同，則小船在靜水中的速度大小為（）。

圖1

解析去程時船頭垂直河岸如圖1所示，設河寬為d，由合運動與分運動具有等時性，則去程時間；回程時行駛路線垂直河岸，故回程時間。由題意有，則，得，選項B正確。

例2如圖2，在高于河面20 m的岸上有人用長繩拴住一條小船，開始時繩與水面的夾角為30°。人以恒定的速率v=3 m/s拉繩，使小船靠岸，那么（）。

A.5 s時繩與水面的夾角為60°

B.5 s內小船前進了15 m

C.5 s時小船的速率為4 m/s

D.5 s時小船距離岸邊15 m

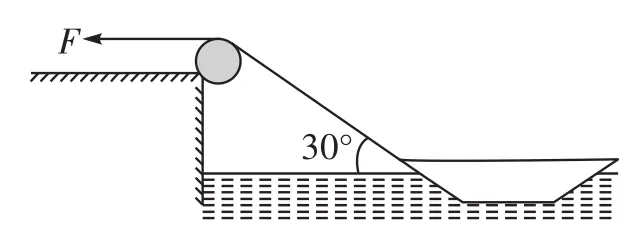
圖2

總結提升運動合成與分解的一般思路

（1）明確合運動或分運動的運動性質。

（2）明確是在哪兩個方向上的合成或分解。

（3）找出各個方向上已知的物理量（速度、位移、加速度）。

（4）運用力與速度的關系或矢量運算法則進行分析求解。

二、平拋運動規律及應用

命題規律平拋運動的規律是每年高考的重點，有時以選擇題的形式出現，有時出現于力學綜合題中，有時還以帶電粒子在電場中的運動為背景考查類平拋運動的處理方法。

例3（2014年全國卷）取水平地面為重力勢能零點。一物塊從某一高度水平拋出，在拋出點其動能與重力勢能恰好相等。不計空氣阻力，該物塊落地時的速度方向與水平方向的夾角為（）。

解析設物塊在拋出點的速度為v0，落地時速度為v，拋出時重力勢能為Ep，由題意知；由機械能守恒定律，得，解得，設落地時速度方向與水平方向的夾角為θ，則，解得，B正確。答案選B。

例4如圖3所示，邊長為L的正方形ABCD中有豎直向上的勻強電場，一個不計重力的帶電粒子，質量為m，電荷量為q，以初速度v0從A點沿AD方向射入，正好從CD的中點射出，而且射出時速度方向與CD成θ=30°的夾角。

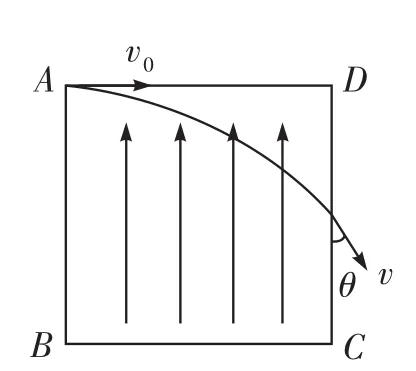
圖3

（1）該帶電粒子帶什么電？

（2）該電場的電場強度E為多少？

解析（1）做曲線運動的物體受的合力總是指向曲線凹的一側，故帶電粒子受到的電場力的方向為豎直向下，與電場強度的方向相反，所以粒子應帶負電。

（2）帶電粒子在電場中做類平拋運動，

則在水平方向上：L=v0t，

在豎直方向上：vy=at，

由牛頓第二定律得：Eq=ma，

總結提升（1）“化曲為直”是處理平拋（類平拋）運動的基本思路和方法。

（2）平拋運動與斜面的結合有下列兩種情形：

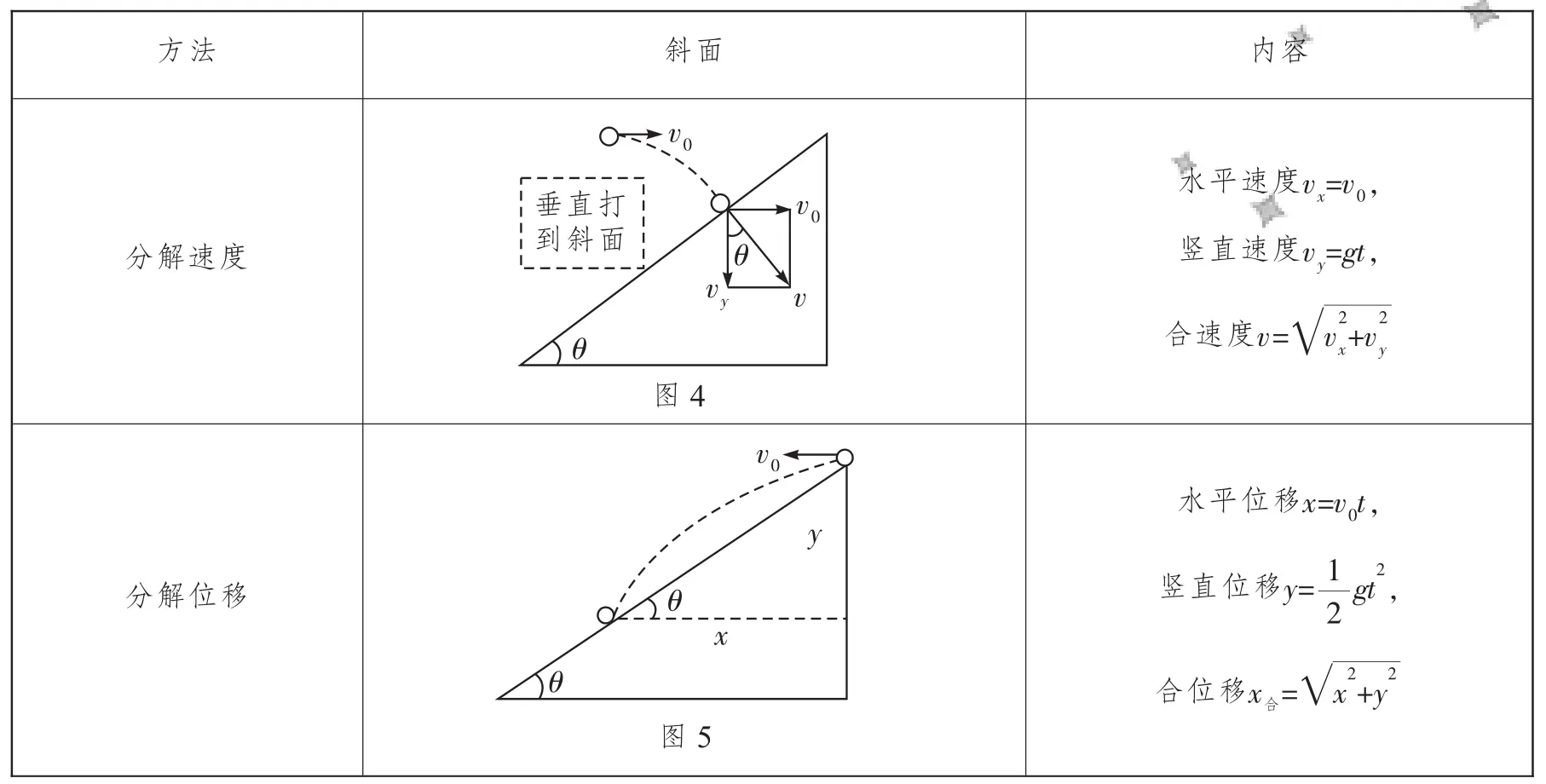
方法　斜面　內容v0 ___v0分解速度垂直打到斜面　θ vyv θ水平速度vx=v0，豎直速度vy=gt，合速度v=　v2x+v2y■圖4 v0 y分解位移___θ水平位移x=v0t，豎直位移y=1 x 2gt2，θ合位移x合=　x2+y2■圖5

三、圓周運動問題的分析

命題規律該知識為每年高考的重點和熱點，題型既有選擇題，也有計算題。近幾年的高考命題規律主要有以下幾點：

（1）圓周運動與平衡知識的綜合題。

（2）考查圓周運動的臨界和極值問題。

（3）與平拋運動、功能關系相結合的力學綜合題。

例5（2014年全國卷）如圖6，一質量為M的光滑大圓環，用一細輕桿固定在豎直平面內；套在大環上質量為m的小環（可視為質點），從大環的最高處由靜止滑下。重力加速度大小為g，當小環滑到大環的最低點時，大環對輕桿拉力的大小為（）。

A.Mg-5mgB.Mg+mgC.Mg+5mgD.Mg+10mg

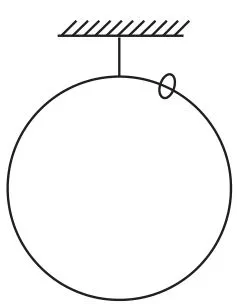
圖6

解析方法一：以小環為研究對象，設大環半徑為R，根據機械能守恒定律，得，在大環最低點有，得FN= 5mg，此時再以大環為研究對象，受力分析如圖7，由牛頓第三定律知，小環對大環的壓力為FN′=FN，方向豎直向下，故F=Mg+5mg。由牛頓第三定律知C正確。

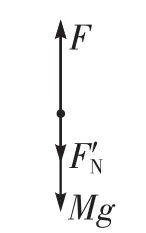
圖7

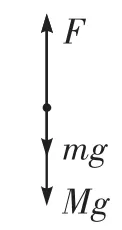
圖8

方法二：設小環滑到大環最低點時速度為v，加速度為a，根據機械能守恒定律，且，所以a=4g，以整體為研究對象，受力情況如圖所示。F-Mg-mg=ma+M·0，所以F=Mg+ 5mg，C正確。

例6（2014年安徽卷）如圖9所示，一傾斜的勻質圓盤繞垂直于盤面的固定對稱軸以恒定角速度ω轉動，盤面上離轉軸距離2.5 m處有一小物體與圓盤始終保持相對靜止。物體與盤面間的動摩擦因數為（設最大靜摩擦力等于滑動摩擦力），盤面與水平面的夾角為30°，g取10m/s2。則ω的最大值是（）。

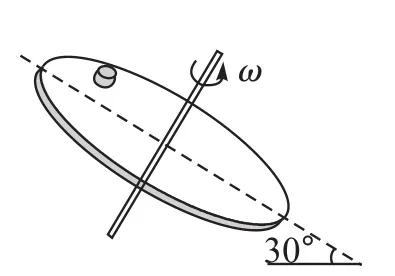
圖9

解析當物體轉到圓盤的最低點恰好不滑動時，轉盤的角速度最大，其受力如圖10所示（其中O為對稱軸位置）

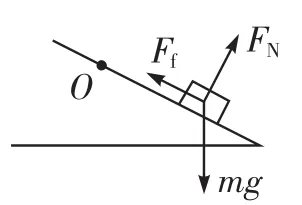
圖10

由沿斜面的合力提供向心力，有μmgcos30°-mgsin30°=mω2R，

總結提升解決圓周運動力學問題要注意以下幾點

（1）要進行受力分析，明確向心力的來源，確定圓心以及半徑。

（3）對于豎直面內的圓周運動，要注意“桿模型”和“繩模型”的臨界條件。

四、平拋與圓周運動的組合問題

曲線運動的綜合題往往涉及圓周運動、平拋運動等多個運動過程，考查運動的合成與分解、牛頓第二定律和功能關系等知識，常以計算題的形式呈現。

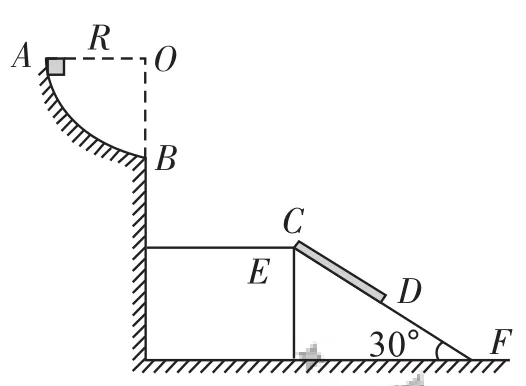
圖11

（1）求物塊到達B點時對圓形軌道的壓力大小。

（2）求物塊做平拋運動的時間。

（3）若下滑過程中某時刻物塊和木板達到共同速度，則這個速度為多大？

由牛頓第三定律可知物塊對軌道的壓力為3 N。

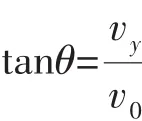
對物塊：v′=v+a1t，a1=g（sinθ-μcosθ）=2.5 m/s2，

對木板：v′=a2t，a2=g（sinθ+μcosθ）=7.5 m/s2，

總結提升解決平拋與圓周運動的組合問題時極易因以下幾點出錯：①不能熟練掌握平拋運動和圓周運動的規律；②找不到銜接兩種運動過程的關鍵物理量；③對豎直面內圓周運動的幾種模型不能熟練掌握，找不出向心力。

應從以下幾點進行防范：①熟練掌握各個運動過程的運動規律；②注意運動速度如何變化，機械能是否守恒；③要善于抓住轉折點或臨界點的速度進行突破；④明確各子過程或全過程有關物理量的變化規律。