探求復合方程根的分布問題基本策略

安徽省五河高中　劉瑞美

探求復合方程根的分布問題基本策略

安徽省五河高中劉瑞美

為了研究問題的方便，我們規定：形如f［g（x）］=0的方程，稱為復合方程，并將方程f（x）=0稱為簡單方程，其中x是未知數。

近年來，有關復合方程的根的問題經常出現在高考試題中，大部分考生遇到這樣的問題往往情緒緊張，不知“路”在何方；也有的考生盡管基礎很好，但由于分類不清和運算不當，使得思路受阻，影響到后續問題的解答。實際上解決此類問題的基本策略是分類討論、數形結合以及換元法等數學思想方法的正確應用，進一步把復合方程轉化成簡單方程或者把方程根的問題轉化成函數圖像交點（函數零點）問題等。下面結合試題具體說一說策略的具體實施過程。

一、分類討論須謹慎

運用分類討論思想解決與復合方程有關問題時，要時刻注意分類的標準，一定要做到不重復與不遺漏，這樣才能得到正確的結果。

例1已知函數f（x）=m·2x+x2+nx，若集合{x|f（x）=0}={x|f［f（x）］=0}≠?，則m+n的取值范圍為（）。

A.（0，4）B.［0，4）C.（0，5］D.［0，5］

解析令t=f（x），由{x|f（x）=0}={x|f［f（x）］=0}可得t=0時，f（t）=f（0）=m=0，因此f（x）=x2+nx，則{x|f（x）=0}={0，-n}，當f［f（x）］=0時，有f（x）=0或f（x）=-n，再由{x|f（x）=0}={x|f［f（x）］=0}≠?可知：f（x）=-n無解或f（x）=-n的解為0或-n，

（1）當f（x）=-n無解時，Δ=n2-4n＜0?0＜n＜4；

（2）當f（x）=-n的解為0或-n時，n=0；于是由（1）、（2）可知：0≤n＜4。

故m+n的取值范圍是0≤n＜4，因而選B。

點評本題實際上考查的是與集合有關的問題。令集合A={x|f（x）=0}，B={x|f［f（x）］=0}，且滿足A=B≠?，從而探求m+n的取值范圍。

二、以形定數顯神威

在解決有關復合方程問題時，分類討論思想自然十分重要，但如果只考慮到分類，僅僅由數再到數，有時可能收效甚微，更有可能陷入無限循環的運算之中，運算量很大，最終導致思路受阻。如果能在分類的同時充分利用數形結合思想，就會使問題的解決變得直觀和輕松。

例2函數f（x）=ax2+bx+c（a≠0）的圖像關于直線對稱。據此可推測，對任意的非零實數a、b、c、m、n、p，關于x的方程m［f（x）］2+nf（x）+p=0的解集都不可能是（）。

A.{1，2}B.{1，4}C.{1，2，3，4}D.{1，4，16，64}

解析本題需要利用換元法，令t=f（x），

則原方程m［f（x）］2+nf（x）+p=0①，

轉化為一元二次方程mt2+nt+p=0②，

（1）分類清晰，思慮周密。

對于方程②，可以分以下三類:

（ⅰ）方程②無實數解；

（ⅱ）方程②有一個實數解，即有兩個相等的實數解t1；

（ⅲ）方程②有兩個不等的實數解t2、t3（不妨設t2＞t3）。

（2）以形助數，方便直觀。

著名數學家華羅庚說：“數缺形少直覺，形缺數難入微。數形結合百般好，隔離分家萬事非。”

對于（ⅰ），易知①的實數解集為?；

對于（ⅱ），如圖1及圖2所示，由圖1得到①的實數解集為{x1，x2}，且

【點評】小作者選取自己的兩件閱讀趣事加以敘述，讓我們看到一個戴眼鏡的小書迷的形象。習作敘事清楚、流暢自然。

由圖2得到①的實數解集為{x3}，且

對于（ⅲ），如圖3及圖4所示，由圖3得到①的實數解集為{x4，x5，x6，x7}，

不妨設x4＜x5＜x6＜x7，且

由圖4得到①的實數解為{x8，x9，x10}，不妨設x8＜x9＜x10，且

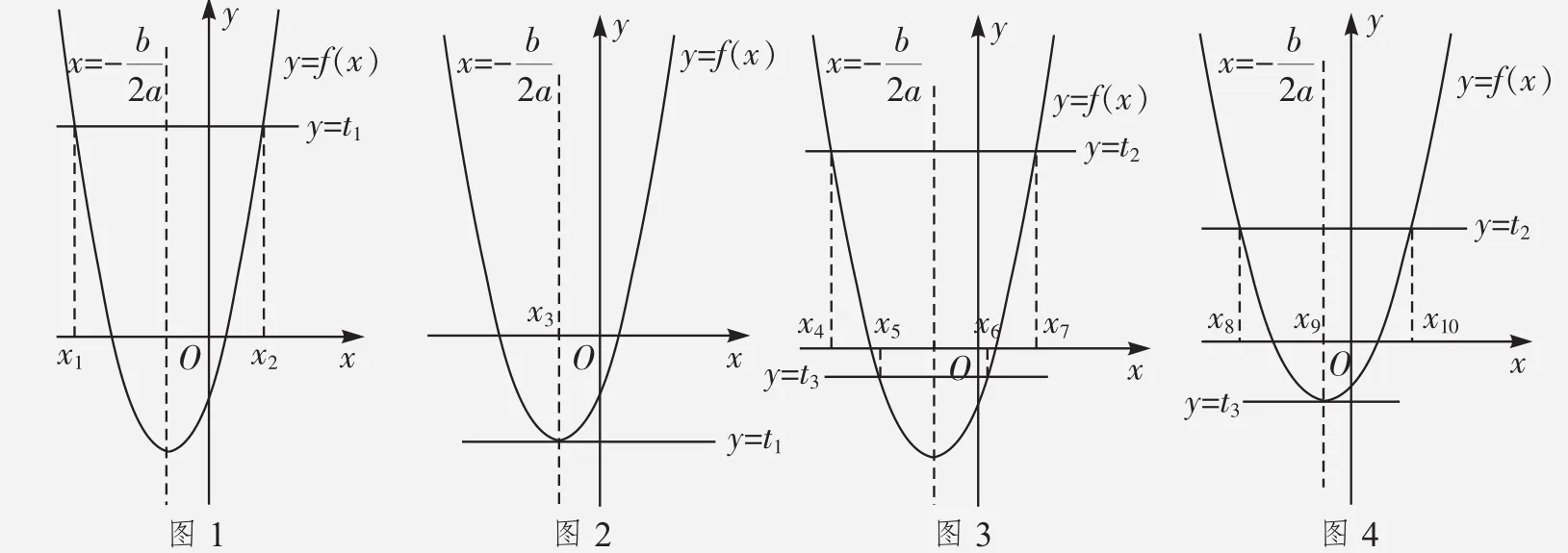
通過以上分析，可以對選項進行驗證，1+64≠4+16，故選D。

點評本題主要考查創新意識和數學應用的能力，是一道集方程與函數、數形結合、轉化與歸納等思想于一體的難得的好題。命題立意沒有刻意追求新、奇、特，雖是意料之外，卻又在情理之中，它無“法”可依，無“型”可套，讓試圖利用題海戰術“以量取勝”的幻想破滅。同時，該題要求我們在今后的學習中要努力揭示問題的數學本質，感悟數學思想方法，提高學習能力，提升數學素養，實現“以質取勝”。

例2若函數f（x）=x3+ax2+bx+c有極值點x1、x2，且f（x1）=x1，則關于x的方程3［f（x）］2+2af（x）+b= 0的不同實根個數是（）。

解析由題意知：f′（x）=3x2+2ax+b，因為函數f（x）=x3+ax2+bx+c有極值點x1、x2，所以x1、x2是方程f′（x）=3x2+2ax+b=0的兩個根，而方程3［f（x）］2+2af（x）+b=0與方程f′（x）=3x2+2ax+b=0在形式上是完全一致的，所以有f（x）=x1或f（x）=x2，又因為f（x1）=x1，因此當x1是極大值點時，x1＜x2，f（x）=x1有兩個根x0、x1，f（x）=x2僅有一個實根x3；當x1是極小值點時，x1＞x2，f（x）=x1有兩個根x0、x1，f（x）=x2僅有一個實根x3，如圖5、圖6所示。

故關于x的方程3［f（x）］2+2af（x）+b=0的不同實根有3個。

點評本題實際上是函數不動點的問題和方程根的問題，主要考查函數的極值和方程的根，需要考生具有極強的運算能力。

三、換元方法巧設置

在解決有關復合方程問題時，換元法是非常常用的，在換元過程中要時刻注意換元之后中間變量取值范圍的變化，稍有不慎將會導致解答錯誤。利用這種方法將復合方程問題轉化成簡單方程或者轉化成兩個函數圖像交點個數的問題，使得問題答案盡顯圖中，使問題的解決呈現直觀性。

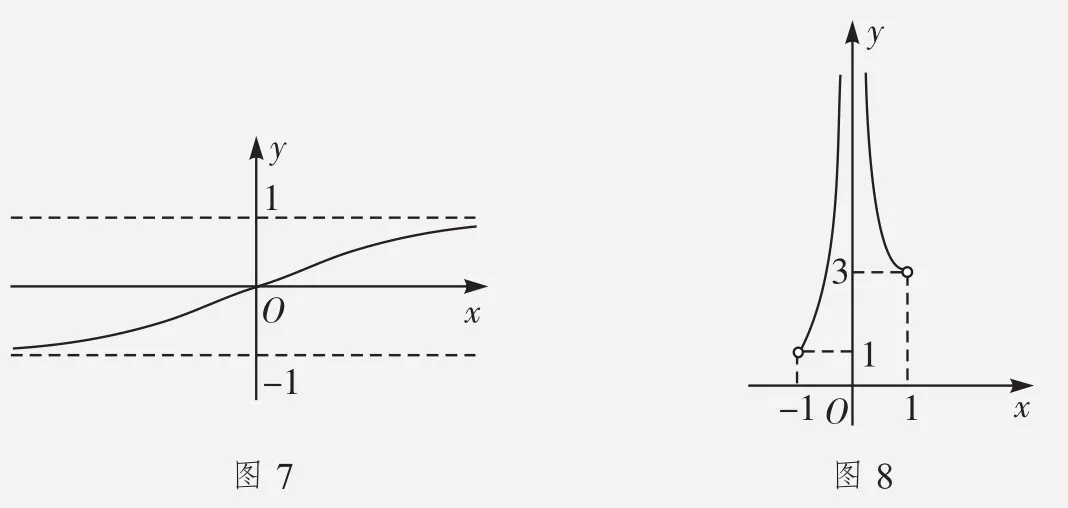
點評復合方程求解常借助于換元法。涉及解的個數的問題，可將復合方程解的個數問題轉化成方程組解的個數問題，再進一步將方程組解的個數問題轉化成兩函數圖像交點的個數問題，實現由數到形，再由形到數的轉化。

通過以上幾道例題的探究我們可以發現，解決這類問題的共同方法：若方程f（x）=0的根分別為x1，x2，…，xn，則對于復合方程f［f（x）］=0的根，就可以轉化為研究方程f（x）=x1，f（x）=x2，…，f（x）= xn根的討論問題，這樣就將復合方程問題轉化成簡單方程問題，又可以更進一步將方程根的問題轉化為函數圖像交點問題，然后利用數形結合使答案躍然紙上。