不確定因素干擾下的最優決策
劉樂然,劉景州
(1.安陽市第一中學;2.安陽幼兒師范高等專科學校,河南安陽455000)
不確定因素干擾下的最優決策
劉樂然1,劉景州2
(1.安陽市第一中學;2.安陽幼兒師范高等專科學校,河南安陽455000)
當面臨多個決策時,人們往往受多個因素的影響。圍繞不確定因素對最優決策的影響,本文從學生去餐廳就餐問題進行入手,將餐廳就餐情況、別人的選擇、自身偏好等不確定因素抽象成可以量化的數值,進行數學建模,進行數據分析,探討如何使決策最優化。
數學建模;決策分析;數據模擬
D01∶10.19329/j.cnki.1673-2928.2016.06.016
在決策過程中,我們將影響決策準則的因素分為人為因素與客觀因素。人為因素包含自身因素與他人行為。客觀因素分為確定因素與不確定因素。在充分考慮主觀因素與確定因素后,我們還需要討論不確定因素、他人行為對決策的影響,使決策更為優越。
1 模型背景
某校有3個食堂,beta去餐廳就餐。他是一個精于策劃的學生,希望用最短的時間以及最令人愉悅的方式解決問題。然而,食堂是一個充滿不確定因素的地方,beta需要根據自己的肚子和三個食堂不同的情況做出最理想的決策。請運用數學建模的知識,圍繞食堂就餐的過程,對該決策進行優化,使beta的決策在食堂中多種因素變化的情形下仍能保持可行性。
圍繞食堂就餐決策的靈敏度分析,本文提出了以下的問題:
1)將餐廳的情況、別人的選擇、自身的偏好抽象成可以量化的數值,并由此得出這些量在這個問題中占的比重;
2)由于實際情況中,beta只能根據以往經驗、自身偏好進行預判,這種預判與實際情況會產生偏差,從而使決策不能收到最大效益。我們可以考慮這些不確定因素產生的影響,從而得到實際與目標的偏離程度,并由此做出評估;
3)不確定因素對beta的決策產生的影響的量化。
2 模型假設
1)假設菜品的受歡迎程度與性價比按照題中所給函數。
2)假設該食堂菜品口味、營養價值按照本文提供表格中的數據成線性分布。
3)假設beta同學就餐決策由且僅由這5個及其相關量來表示。
4)假設三個食堂各有差異且差異可以表示。
5)假設beta本身只能決定菜品種類,排隊人數對于beta完全不可控。
3 符號說明
下列符號的含義是:
A1:菜品口味,常量
A2:擁擠程度,常量
A3:營養價值,常量
A4:菜品價格,常量
A5:排隊時間(min),常量X0:菜品的性價比,變量
E:排隊人數的實際值,變量
F0:排隊人數的預測值,常量
W:排隊人數的誤差值,常量
μi:菜品的受歡迎程度,常量
Ni∶考慮誤差后的擁擠程度,變量
Ti∶考慮誤差后的排隊時間,變量
Λmaxi∶每個因素的重要程度,常量
S=100∶窗口面積(m2),常數
V=100∶排隊速度,即單位時間排完隊的人數(人/H),常數
Mi∶不同菜品對應的隊長(人),變量
Ω∶層次分析中的矩陣列
P:決策指數,函數
Q:決策指數的過渡函數,函數
4 問題分析
Beta對不同的菜品有自己不同的評價,菜品的優劣(b1)主要有菜品的營養度a1,菜品的價格a2,來決定,菜品的優劣又往往會影響到選擇食用該菜品的人數,我們把這個關系用同類商品的便宜程度與其受消費者歡迎程度的函數(Gx)來近似,用matlab求解。
每一天到食堂吃飯的人數e也是波動的,因此beta每天的排隊時間也有波動,買好吃的菜又會增加排隊時間。
綜上,我們把beta就餐的決策收益分為菜品口味和營養體驗。消費成本分為擁擠過程中的心理成本、排隊時間和菜品的價格。
首先對于排隊人數進行灰色預測,并得到期望值與誤差值。
通過層次分析,得到beta應該去哪個食堂,以及beta做決策時對這五個因素的偏重程度,即權重系數。
又通過數學分析得到以下幾個量間的關系:排隊人數與擁擠度,排隊人數、選擇菜品的受歡迎程度對排隊時間的影響,共得到5個關鍵函數。
根據期望值與誤差值,得到排隊人數的可變區間,并通過蒙特卡洛模擬方法隨機生成8組該區間的數值,再加上兩個端點的極端數值生成5*n的數值矩陣,并由該矩陣計算協方差矩陣,并計算協方差矩陣的和,觀察是否超出可接受范圍。
5 模型求解
5.1 受歡迎度的函數
為探究受歡迎程度與營養程度、菜品價格間的關系,我們設立多元線性回歸方程,μi=b1+b2× A4+b3×A3,得到μi=-173.4+150.9×A4+10.22×A3 (μi受歡迎度、A4價格、A3營養值)
5.2 排隊時間、排隊人數的函數
為了衡量食堂的擁擠程度F(x)=mi/S;
mi=e*(μi/∑ui)表示排隊買第i個菜的隊長。Ti=mi/v表示買第i個菜的排隊時間。
5.3 排隊人數的灰色預測
本題中的排隊人數符合灰數模型。
采用灰色預測GM(1,1)的方法,由前10天的賣出份數得到:今天的賣出份數預測值為:1045.0484;百分絕對誤差為:25.8384。
5.4 對于食堂就餐的層次分析(AHP)
采用層次分析法對就餐問題進行分析:將就餐選擇分為兩個層次,第一個層次為:菜品口味、擁擠程度、營養價值、菜品價格、排隊時間;第二個層次為:3個不同窗口(見圖1)。通過定性指標模糊量化方法算出層次單排序和總排序,以作為目標、多方案優化決策的系統方法。

圖1 對食堂就餐問題的層次分析(AHP)
5.4.1 構造判斷矩陣
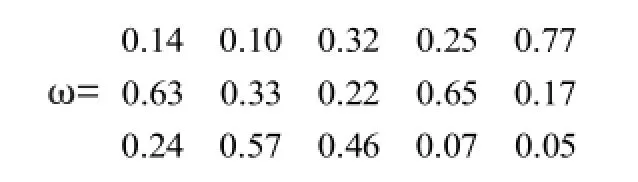
5.4.2 求出最大特征值及特征向量
A的最大特征值λmax=5.363
相應的特征向量為 ω=(0.202,0.338,0.245, 0.051,0.164)T
比較方案層對準則層的影響,同理得到五個成對比較矩陣A1,A2,A3,A4,A5,求得各要素最大特征值和相應的特征向量。
5.4.3 一致性檢驗
一致性指標CI=(5.363-5)/(5-1)=0.0908隨機一致性指標RI=1.12
一致性比率CR=0.0908/1.12=0.081<0.1通過一致性檢驗。
經計算,均通過一致性檢驗。
由此,我們得到beta同學明智的選擇是去三食堂。
5.4.4 構建函數Q=Q1-Q2
Q1為決策利潤,Q2為決策成本。
決策利潤包括菜品口味,營養價值,決策成本包括擁擠程度,排隊時間,菜品價格。這里的擁擠程度、排隊時間、菜品價格按照灰色預測所得到的結果,而菜品的口味則按照beta自己的選擇。
由Q1=0.202×A1+0.245×A3;
Q2=0.338×A2+0.051×A4+0.164×A5.
得 Q=(0.202×A1+0.245×A3)-(0.338×A2+ 0.051×A4+0.164×A5).
為了使他們的重要程度僅由權重系數決定,我們對這個公式進行修正:
P=(0.202×A1+0.245×A3/20)-(0.338×A2/100+ 0.051×A4+0.164×A5)
5.4.5 結論
模糊量化條件:每種菜的口味可以由不同的
數值衡量。
根據灰色預測的結果,百分絕對誤差為:25.8384;預測值為:1045.0484。
我們知道,排隊人數應在(760.216,1288.821)之間。為不失準確性,我們將排隊人數的可能區間設為(760,1288)。
5.5 數據模擬與邊界分析
使用蒙特卡洛法,考慮邊界條件進行隨機模擬,綜合菜品受歡迎程度與排隊時間、營養價值的函數,我們可以分別得到六樣菜品的Q值
-0.452-0.434-0.498 0.240 0.021 0.168
Beta同學在做出選擇4號菜品的決策后,排隊人數的波動造成決策的成本與結果的綜合準則p隨之浮動,而決策的靈敏度要求是波動范圍使得決策最優的地位沒有改變。由蒙特卡洛模擬得,e在一定偏小范圍內變化時,beta的4號決策仍為最優決策,當e達到e0時,顯然,6號菜品取代4號菜品成為最優決策。現在,我們建立數學模型來求出e0,模型求解如下:
對于一個e0,根據公式
P=(0.202×A1+0.245×A3/20)-(0.338×A2/100+ 0.051×A4+0.164×A5)
4號菜品的決策指數為
P4=(0.202×1+0.245×75/20)-(0.338×e0× 0.16678/100+0.051×0.6+0.164×e0×0.16678×0.01)
6號菜品的決策指數為
P6=(0.202×1+0.245×23.5/20)-(0.338×e0× 0.05310/100+0.051×1+0.164×e0×0.05310×0.01)
當P4=P6時,可以解得,e0=1135.1
綜上,在760<e<e0時,beta同學選擇4號菜品,3號食堂為標準決策,在e0<e<1288時,beta同學選擇6號菜品為標準決策。當e=e0時,beta同學可以根據其他條件任意選擇4號和6號中的一個。
5.6 模型的驗證·協方差檢驗
不同量之間的相互影響的程度見表1。由協方差矩陣知,P函數獨立性極強,可以認為是正確的。

表1 協方差檢驗表矩陣
6 模型評估
1)在等待的過程中,該學生的饑餓度有可能隨時間的推移而改變,這點我們在模型分析中若能夠稍做說明,問題將顯得更加可靠。
2)對于灰數模型GM(1,1),該模型參數通常采用最小二乘法來估計,雖然最小二乘法是迄今為止最常用的辦法,但采用最小二乘法的前提是擬合誤差應具有正態性,否則,由它求得的參數穩健性較差,對異常數據較敏感。[1]
[1]穆勇.灰色預測模型參數估計的優化方法[J].青島大學學報(自然科學版),2003,16(3)∶95-98.
(責任編輯:王彥永)
O211.9
A
1673-2928(2016)06-0052-03
2016-04-08
劉樂然(1999-),河南安陽人,安陽一中。劉景州(1974-),河南上蔡人,安陽幼兒師范高等專科學校副教授,主要研究方向:計算機信息。

