基于Vasicek模型的公司債券定價研究

劉晶 方華

摘 要：文章從利率期限結(jié)構(gòu)的角度對公司債券進(jìn)行研究，并將Vasicek模型應(yīng)用于公司債券價格估計與未來收益率估計上。通過選取兩只剩余期限不同的公司債券對理論進(jìn)行實證檢驗，檢驗結(jié)果表明，Vasicek模型對于公司債券定價與確定未來收益率上具有一定參考價值。對剩余期限在一年左右的公司債券，文章的理論價格與市場價格擬合較高。

關(guān)鍵詞：公司債券；Vasicek模型；利率期限結(jié)構(gòu)；實證研究

中圖分類號：F275.6 文獻(xiàn)標(biāo)識碼：A

Abstract： In this paper， we study the corporate bonds from the perspective of the term structure of interest rate， and apply the Vasicek model to the estimation of corporate bonds pricing. By selecting two corporate bonds， which have different remaining term， to carry out an empirical test of the theory. In corporate bonds pricing and future yield rate estimation. The test results show that Vasicek model has certain reference value. For the corporate bond which has one-year remaining maturity， there are higher fitting about theory price and market price.

Key words： corporate bond； Vasicek model； term structure of interest rate； empirical research

0 引 言

近幾年，我國債券市場發(fā)展迅速，僅2016年第一季度，債券市場發(fā)行規(guī)模合計81 759.72億元，較上季度增長11.85%，較上年同期增長超過100%。2015年，我國債券市場發(fā)行各類債券16.82億元，同比增長53.13%，其中，公司債的發(fā)行增長較為突出。2015年，我國公司債券市場共發(fā)行公司債券940期，募集資金規(guī)模為12 615.49億元，同比分別增長80.77%和362.01%。面對迅速發(fā)展的公司債券市場，我國公司債券的研究相對不足，這就要求對公司債券定價的分析更加深入。

研究債券價格的關(guān)鍵在于研究債券未來收益率，也就是遠(yuǎn)期收益率。而利率期限結(jié)構(gòu)理論正是人們研究收益率的主要理論之一，現(xiàn)代利率期限結(jié)構(gòu)理論研究主要以利率期限結(jié)構(gòu)模型為工具[1]。其中，Vasicek模型的結(jié)構(gòu)較為簡單，估計比較方便，該模型被廣泛運用于資產(chǎn)定價、風(fēng)險管理等領(lǐng)域[2]。因此，本文希望以滬深交易所交易的公司債券為研究對象，借助Vasicek模型的理論，比較模型與實際價格的差別，從而對公司債券定價問題給出合理化的答案。

1 模型與分析方法介紹

1.1 利率期限結(jié)構(gòu)理論。利率期限結(jié)構(gòu)所描述的是在某一時刻，債券的到期收益率與其到期期限之間的關(guān)系，它反映了時間因素對收益率曲線變化的影響[3]。通常，以時間為變量的收益曲線形狀大致分為四種情況，即向上傾斜，向下傾斜，凹凸形以及平坦直線形狀。利率期限結(jié)構(gòu)作為資產(chǎn)定價、金融產(chǎn)品設(shè)計、套利、利率風(fēng)險管理及投資等的理論基礎(chǔ)，一直是金融研究的主要領(lǐng)域[4]。

20世紀(jì)70、80年代，西方各國放松了利率的管制，實行了利率市場化后，利率開始具備了隨機性。為了研究利率市場的隨機行為，人們引入了隨機微積分方程。隨機期限結(jié)構(gòu)模型就是通過構(gòu)建某一時點的利率隨機微分方程，描述利率與期限的不確定函數(shù)關(guān)系，由此對債券進(jìn)行定價。主要的隨機期限結(jié)構(gòu)理論分為均衡模型和無套利模型兩大類。其中，均衡模型又被分為單因子模型和多因子模型，兩者的區(qū)別主要在于影響利率因子的個數(shù)。單因子模型結(jié)構(gòu)較為簡單，它將收益率曲線看作單一變量的函數(shù)。同時，單因子模型理論的假設(shè)也較為嚴(yán)格，例如：它從理性人的角度出發(fā)，認(rèn)為市場投資者是風(fēng)險中性的。

常見的單因子模型主要包括：Merton模型、Vasicek模型和Cox-Ingersoll-Ross模型（簡稱CIR模型）。以下將會對Vasicek模型進(jìn)行介紹，并應(yīng)用該模型解決利率期限結(jié)構(gòu)問題。

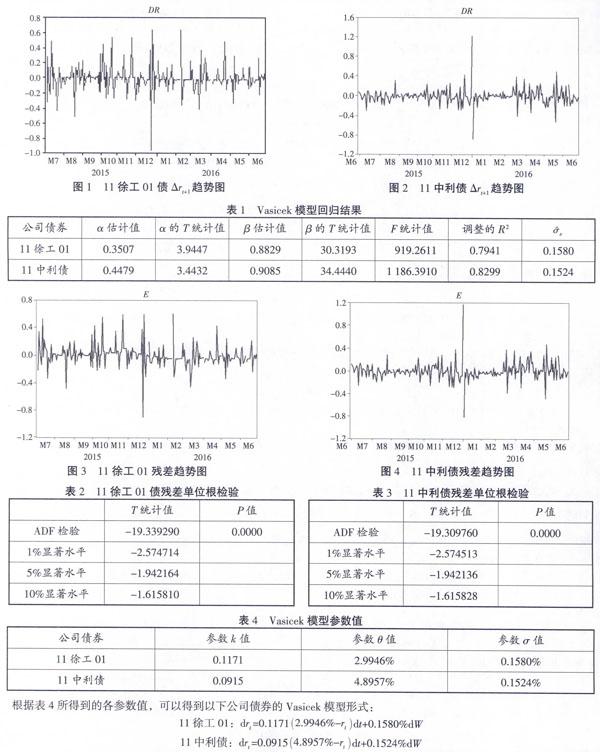
下面對模型進(jìn)行單位根檢驗，圖3與圖4為式（3）模型經(jīng)過回歸處理后的殘差序列趨勢圖。

根據(jù)圖3和圖4，可以看出兩只債券的殘差序列均無趨勢項和截距項，對殘差序列進(jìn)行單位根檢驗，結(jié)果如表2、表3所示：

根據(jù)表2和表3的檢驗數(shù)據(jù)，兩只債券在ADF檢驗下的T值都較大，P值較小。模型在1%顯著水平下T值也非常顯著，說明殘差序列是平穩(wěn)的，即不存在單位根。因此兩只債券的式（3）模型均存在協(xié)整關(guān)系。

兩只債券樣本數(shù)據(jù)的均值分別為3.0313%和4.9174%。從Vasicek模型的長期均值來看，兩只公司債的θ值分別為2.9946%和4.8957%，與實際情況較為符合，且波動率較小。

2.4 債券價格的確定。由于兩只公司債券的剩余期限都在一年之內(nèi)，且均結(jié)束了上一期付息，到期日將一次還本付息，所以可以把兩只債券看成面值為本息和的零息債券，按照Vasicek模型進(jìn)行貼現(xiàn)，預(yù)測結(jié)果如表5所示。

表5中，實際價格采用的是當(dāng)天的收盤價格。從上面的表3來看，對于剩余期限較長的11中利債的估值誤差較小，估計價格與實際價格較為相符，平均價格誤差在0.12元左右。而剩余期限較短的11徐工01債的估值存在較大偏差，且估值普遍高于實際價格2.6元左右。這與Vasicek模型在國債定價中的情況恰好相反——隨著剩余期限增加，國債的定價誤差越大[6]。