基于AR（1）模型的純保費的Monte Carlo模擬研究

關清元，洪夢瑩

（武夷學院數學與計算機學院，福建武夷山354300）

基于AR（1）模型的純保費的Monte Carlo模擬研究

關清元，洪夢瑩

（武夷學院數學與計算機學院，福建武夷山354300）

把隨機利率，轉化成年利率，然后用AR（1）模型進行擬合，并利用SPSS軟件對擬合做出檢驗。經檢驗擬合效果比較好，模型可用。以當前熱銷的前海人壽保險有限公司的萬能保險為實證分析，用Monte Carlo模擬的方法，借助MATLAB軟件求出了躉繳純保費，并預測了在3σ原則下的純保費區間。

年平均加權利率；AR（1）模型；SPSS軟件；Monte Carlo模擬；3σ原則

在國內，運用MonteCarlo技術對純保費所做的研究不多。1997年蔣慶榮[7]在《隨機利率下的終身壽險》中得到了終身壽險的純保費的計算公式；2001年，良艷懷,瑪恩民[8]在《隨機利率下綜合人壽保險模型》中，考慮了隨機過程函數，給出了綜合人壽保險模型；2003年王麗艷,柳揚[9]在《隨機利率下的準備金與壽險風險分析》中采用了Bayes方法，得到了死亡率的經驗分布；2005年東明[10]在《申匯養老保險中隱性債務的雙隨機模型》中采用了Wiener Process model對養老保險隱性債務進行建模。

以上這些論文沒有考慮用AR過程來模擬,運用適當的方法證明了用AR過程來建模，在現實生活中是可行的，然后采用Monte Carlo模擬的方法得到了特定條件下純保費的分布區間。在實證分析中，運用Matlab軟件并結合Spss軟件，首次對萬能保險的躉繳純保費，進行了大量快速的模擬，對提高萬能保險躉繳純保費的精度進行了新的嘗試。

1 隨機利率下的AR(1)模型

1.1 數據處理

中國人民銀行官方網站：一年期定期存款利率的調整如表1所示：

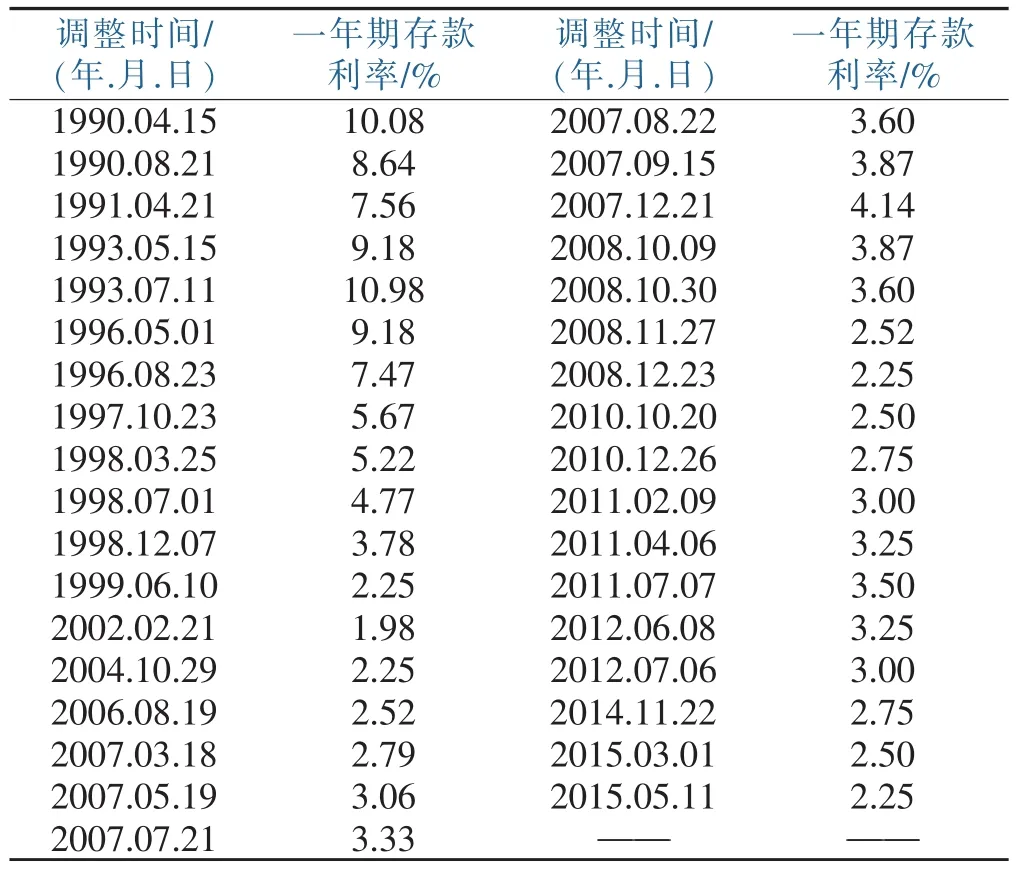
表1 存款利率

由于每次調整，都會相應的維持一個時間區間，即可以把這些時間點看成是一個連續的時點序列。所以下面采用按照時間段加權的方法[11]，將其轉化為一個整數年的利率，公式為,其中表示當年的平均利率水平，ik表示當年第k個利率水平，fk則表示第k個利率水平所維持的天數。由此計算可得各年的年平均利率如表2所示：

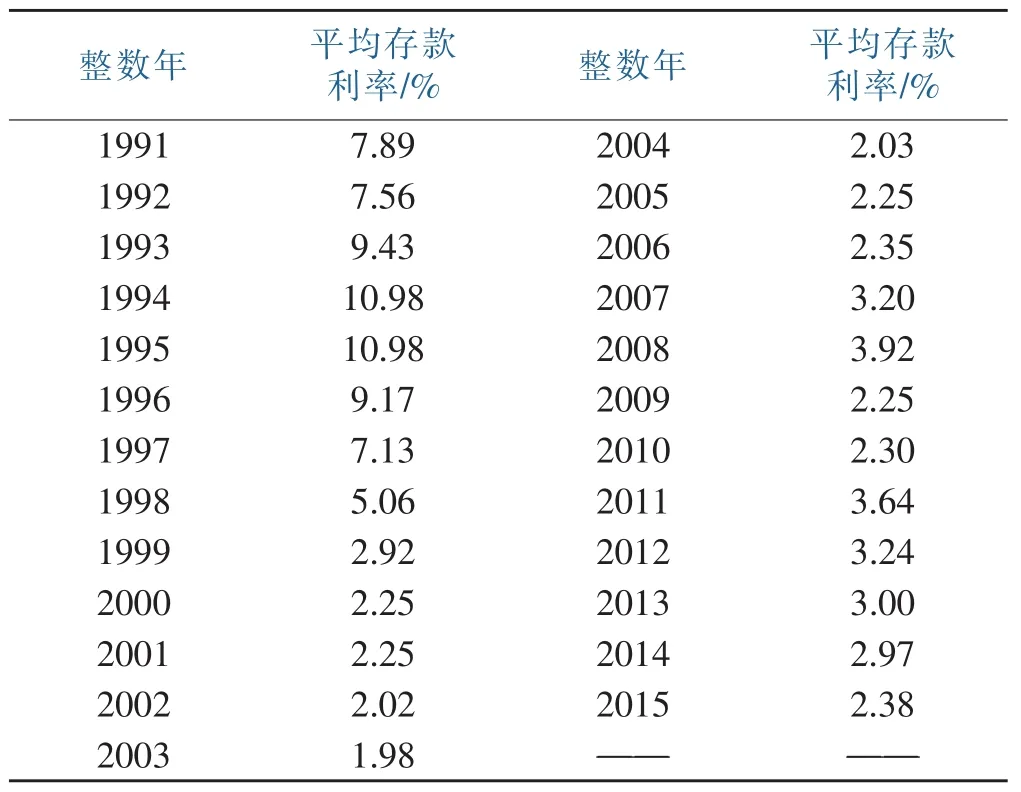
表2 年平均利率

1.2 利率模型的擬合

根據設定的情景條件，對5個影響因素每隔0.5 h采集一次樣本數據，采用調查問卷法得到影響因素的定性判定數據。各因素風險狀態劃分為強+(A)，強(B)，中等(C)，弱(D)，弱-(E)5個狀態。

由于AR（1）模型是回歸模型的范疇，用SPSS軟件做散點圖如下：

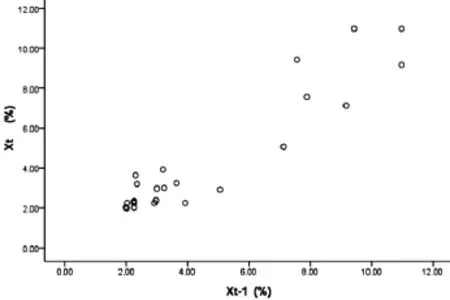
圖1 前一年利率Xt-1與后一年利率Xt的關系散點圖

從圖1可以看出：Xt-1與Xt在較大程度上呈線性關系。所以初步判斷對其用AR（1）模型來擬合是可行的。

下面用SPSS軟件對Xt-1與Xt的數量關系來進一步地求解，從而求出AR（1）模型的參數。以下為SPSS的分析結果表：

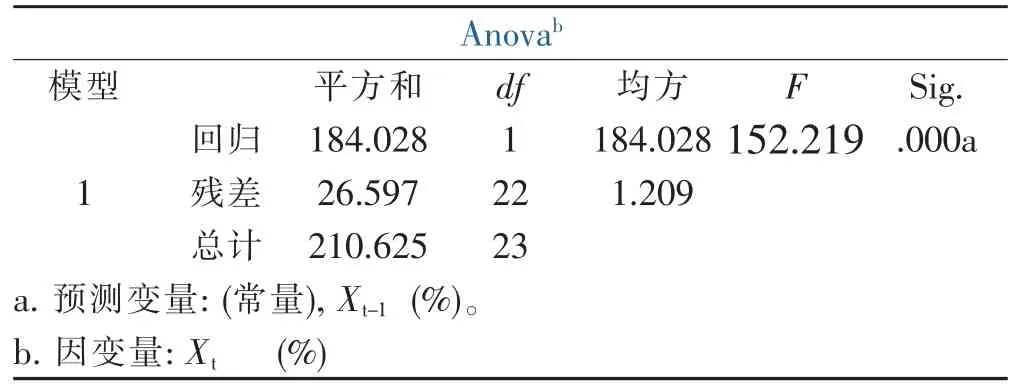
表3 回歸變異圖

由表3可以看出，Regression為184.028，Residual Total為26.597，對應的F統計量的值為152.219，且152.219fF0.05（1，22）=4.30,又因為顯著性水平sig.= 0.000?0.05所以可以認為所建立的回歸方程有效。

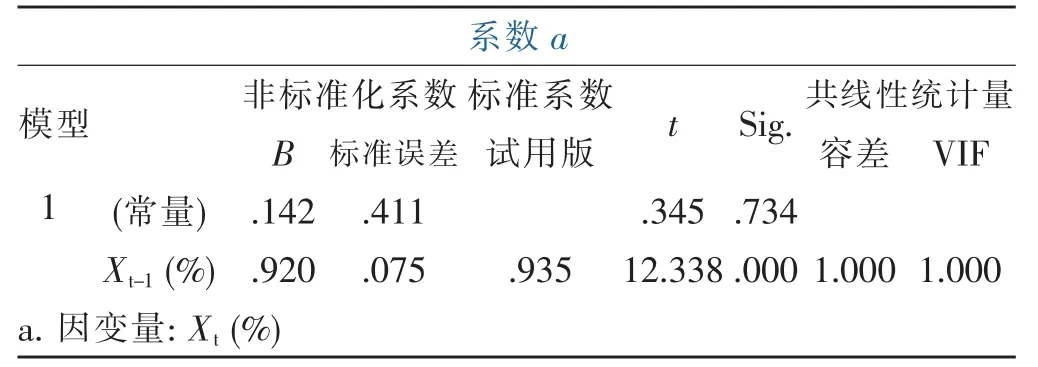
表4 回歸系數表

由表4可以看出，非標準化的Regression coefficient的估計值為0.920，標準Error為0.075，標準化的Regression coefficient為0.935，回歸系數顯著性檢驗的t統計量的值為且12.338，且12.338?t0.025（22）= 2.074,對應的顯著性水平sig.=0.000?0.05,故可以認為方程是顯著的。

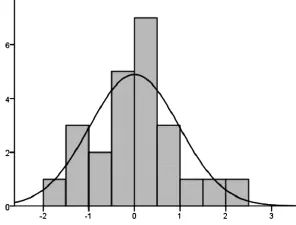
圖2 標準化殘差直方圖

圖2，反映了殘差的分布情況，根據圖形來看，殘差項基本符合標準正態分布。

綜上所述，可得利率模型為：

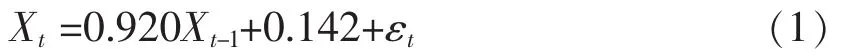
2 前海人壽萬能保險的montecarlo模擬實證

考慮到現在大多數人傾向于購買萬能保險，且據一些保險公司透露，在銷售的所有保險產品中，萬能險的比例已經達到了30%～40%。萬能保險既能夠提供人身保障，又能夠作為投資。

以前海人壽保險股份有限公司銷售的萬能險為例，由于萬能險的保險額度設計有多種，本文特根據《萬能保險精算規定》做出如下假設：提供2.5%的結算收益率保底。

某男50歲投保前海人壽萬能保險，保險期間是10年，該男在保險期內身故，在年末公司支付1萬元的身故保險金；如生存至期滿，同樣可獲得1萬元的滿期保險金。試分析該男的躉繳純保費[12]。以當前2.38%的利率水平為基礎，對未來10a的利率情形進行隨機模擬，得出躉繳純保費的可能值，對上述過程進行6000次MonteCarlo模擬，得出結果。

根據萬能保險的躉繳純保費公式：

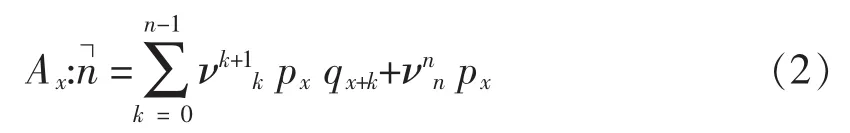
而在每年是變化利率的情況下，此式演變為:

根據中國人壽保險業男性經驗生命表（2000～2003）可得：

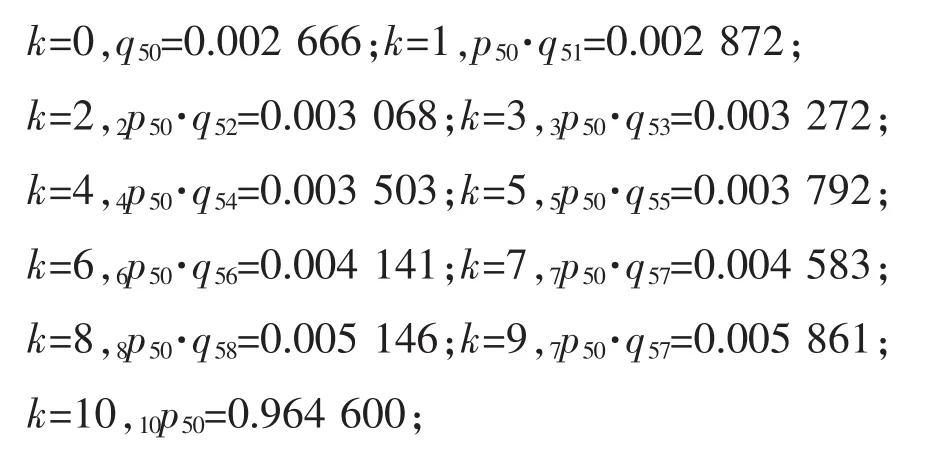
前海人壽10年期萬能保險躉繳純保費Monte Carlo仿真的MATLAB代碼為:

forj=1:6000;

fori=1:9;

x(1)=2.38;

x(i+1)=x(i)*0.920+0.142+randn(1,1);

end;

y(j)=0.002666/(1+x(1)/100)+0.002872/(1+x(1)/100)/(1+x (2)/100)+0.003068/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/ 100)+0.003272/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/100)/ (1+x(4)/100)+0.003503/(1+x(1)/100)/(1+x(2)/100)/(1+x(3) /100)/(1+x(4)/100)/(1+x(5)/100)+0.003792/(1+x(1)/100)/ (1+x(2)/100)/(1+x(3)/100)/(1+x(4)/100)/(1+x(5)/100)/(1+x (6)/100)+0.004141/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/ 100)/(1+x(4)/100)/(1+x(5)/100)/(1+x(6)/100)/(1+x(7)/100) +0.004583/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/100)/(1+x (4)/100)/(1+x(5)/100)/(1+x(6)/100)/(1+x(7)/100)/(1+x(8)/ 100)+0.005146/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/100)/ (1+x(4)/100)/(1+x(5)/100)/(1+x(6)/100)/(1+x(7)/100)/(1+x (8)/100)/(1+x(9)/100)+0.005861/(1+x(1)/100)/(1+x(2)/ 100)/(1+x(3)/100)/(1+x(4)/100)/(1+x(5)/100)/(1+x(6)/100)/ (1+x(7)/100)/(1+x(8)/100)/(1+x(9)/100)/(1+x(10)/100)+ 0.9646/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/100)/(1+x(4)/ 100)/(1+x(5)/100)/(1+x(6)/100)/(1+x(7)/100)/(1+x(8)/100)/ (1+x(9)/100)/(1+x(10)/100)

end;

y

mean(y)

std(y)

通過此代碼，可以得到在Monte Carlo模擬下的平均躉繳純保費mean（y）=8162元，標準差std(y)= 1070,則根據正態分布的3σ原則，可得躉繳純保費以68.26%的概率落在區間[7092,9232]上,以99.74%的概率落在區間[4952,11372]上。又根據此險種的保底收益率，可得實際躉繳純保費以68.26%的概率落在區間[5540,7212]上,以99.74%的概率落在區間[3 868,8883]上。

3 小結

根據每個時間點的利率數據進行時間加權平均、AR(1)模型的構建以及用spss去做擬合的檢驗。最后用Monte Carlo模擬的方法對前海人壽保險公司一款熱銷的萬能保險產品進行躉繳純保費的實證分析，此測算是借助MATLAB軟件平臺所做。對人壽保險公司的其他的一些產品，可以類似的進行擬合化的控制預測，對保險公司定價風險的控制提供了新的思路，對于保險公司產品設計、運營和監控具有一定的借鑒意義。

[1]Milevsky M A.The presnt value of a stochastic perpetuity and the gamma distribution[J].Insurance:Mathematics and Economics,1997(20):243-250.

[2]Milevsky M A.Martingales scale functions and stochastic life annuities a not[J].Insurance:Mathematics and Economics, 1999(24):149-154.

[3]Kaas R,Dhaene J,Goovaerts M J.Upper and lower bounds for sums of variables[J].Insurance:Mathematics and Economics, 2007(27):151-168.

[4]De A,Goovaerts M J,Dhaene J,et al.Bounds for present value funcions with stochastic interest rates and stochastic volatility [J].Insurance:Mathernatics and Econornics,2002(31):87-110.

[5]Perry D，Stadje W·Function space intenration for annuities [J].Insurance:Mathematics and Economics,2001(29):73-82.

[6]Perry D,Stadje W,Yosef R.Annuities with controlled random interest[J].Insurance:Mathematics and Economics,2003(32): 245-253.

[7]蔣慶榮.隨機利率下的終身壽險[J].杭州大學學報（自然科學版）,1997(2):8-14.

[8]良艷懷,瑪恩民.隨機利率下綜合人壽保險模型[J].大連理工大學學報,2001(5):29-31.

[9]王麗燕.隨機利率下的準備金與壽險風險分析[J].大連大學學報,2003(4):17-35.

[10]東明,郭亞軍,楊懷東.社會養老保險中隱性債務的雙隨機模型[J].系統工程學報,2005(6):570-577,643.

[11]賈懷勤.應用統計[M].北京：對外經貿教育出版社,1994: 45-54.

[12]楊靜平.壽險精算基礎[M].北京：北京大學出版社，2010.

（責任編輯：夏婷婷）

Simulation of Pure Premium of Carlo Monte Based on AR(1)M ode

GUAN Qingyuan，HONG Mengyin
(School of Mathematics and Computer Science,Wuyi University,Wuyishan,Fujian 354300)

In this paper,it changes random interest rate into annual interest rate.Then it uses the AR(1)model to fit the rate.And it tests the fitting by using the SPSS Software model.lt calculates the net single premium by using matlab software and it predicts the pure premium interval of the principle of“three”,taking for example universal life insurance,hotly sold by sea life insurance company, by using the method of Monte Carlo simulation.

average weighted interest rate;AR(1)model;SPSS software;Monte Carlo simulation;threeσprinciple

F224；F842

A

1674－2109(2016)09－0073－04

2016-03-24

武夷學院科技類項目(XD201405)；國家級大學生創新訓練項目(201410397002)。

關清元(1981-)，男，漢族，講師，主要從事計算數學、保險精算方向研究。