城市路網的魯棒預測控制

劉 安 東， 李 佳， 俞 立

( 浙江工業大學 信息工程學院， 浙江 杭州 310023 )

?

城市路網的魯棒預測控制

劉 安 東*， 李 佳， 俞 立

( 浙江工業大學 信息工程學院， 浙江 杭州 310023 )

針對模型不確定的城市路網系統，設計了使閉環系統漸近穩定的魯棒預測狀態反饋控制器．首先，將“存儲與向前”路段線性模型擴展為城市路網拓撲模型．同時考慮實際情況中路況變化、測量誤差等因素引起的飽和流量、車輛數的不確定性的影響，提出了具有不確定參數的城市路網系統模型．然后，采用線性矩陣不等式處理方法求解一個具有約束的凸優化問題，給出了狀態反饋控制器設計方法．最后通過Matlab仿真驗證了所提方法能有效緩解城市交通擁堵和優化信號燈．

魯棒預測控制；城市路網系統；參數不確定；線性矩陣不等式

0 引 言

近幾十年來，隨著車輛數的增加，交通擁堵已經成為阻礙社會經濟發展的重要因素．在城市路網系統中，由于交通流的時段性及交通基礎設施的不可擴展性，擁堵問題尤為嚴重[1]．因此，迫切需要一種有效的控制策略來緩解城市交通擁堵和優化路口信號燈．在已有的控制策略中，實時控制策略具有對當前變化的交通狀況做出及時調整的優點，從而比定時控制策略具有更廣闊的發展前景[2]．實時控制可分為基于實時交通流和基于狀態空間模型的實時控制，其中基于模型的控制方法能更好地運用現代控制理論方法，故近年來得到了較快的發展與應用[3]，并成為當前的一個研究熱點．

目前，城市路段模型主要有“存儲與向前”線性模型、改進型“存儲與向前”非線性模型、細胞模型等[4-11]．在這些模型中，Gazis和Potts等提出的“存儲與向前”線性模型相比于其他模型更直觀簡潔、適用性強，且該模型適用于飽和狀態下的城市路段[4]．基于該線性模型，學者們提出了一系列控制算法：Diakaki等采用LQR算法求解綠燈相位時間的反饋控制控制律[5]，雖然簡單方便，但是不能處理帶有約束的最優化問題；Aboudolas等采用集中式或分布式模型預測控制方法解決帶有約束的綠燈相位時間的最優化問題[6-8]；為了能準確描述交通系統，Lin等通過對“存儲與向前”線性模型的改進得到了非線性模型，并使用了模型預測控制算法，達到了較好的控制效果[9]．但是“存儲與向前”線性模型和非線性模型是一種精確模型，而實際情況中路況變化、測量誤差等因素引起的飽和流量、車輛數的不確定性會導致“存儲與向前”模型的參數不確定[12]，因此基于該模型的算法在具有不確定因素影響下無法獲得很好的控制效果．

針對實際情況中路況變化、測量誤差等因素引起的飽和流量、車輛數的不確定性所導致的“存儲與向前”線性模型的參數不確定，本文采用魯棒預測控制方法設計一個狀態反饋控制器用于調節各個路口的綠燈相位時間．首先改進由“存儲與向前”路段線性模型增廣得到的城市路網拓撲模型，同時考慮參數不確定性和綠燈時間約束，得到帶有參數不確定的路網系統模型；然后利用線性矩陣不等式(LMI)處理方法解決具有約束的凸優化問題，并給出控制器求解方法；最后，通過仿真驗證魯棒模型預測控制策略．

1 城市路網系統建模

文中常用符號定義見表1．

表1 符號定義

1.1 “存儲與向前”路段模型

“存儲與向前”路段模型由兩個相鄰路口(M、N)及連接兩個路口的一條道路z組成，且z∈OM，z∈IN，如圖1所示．

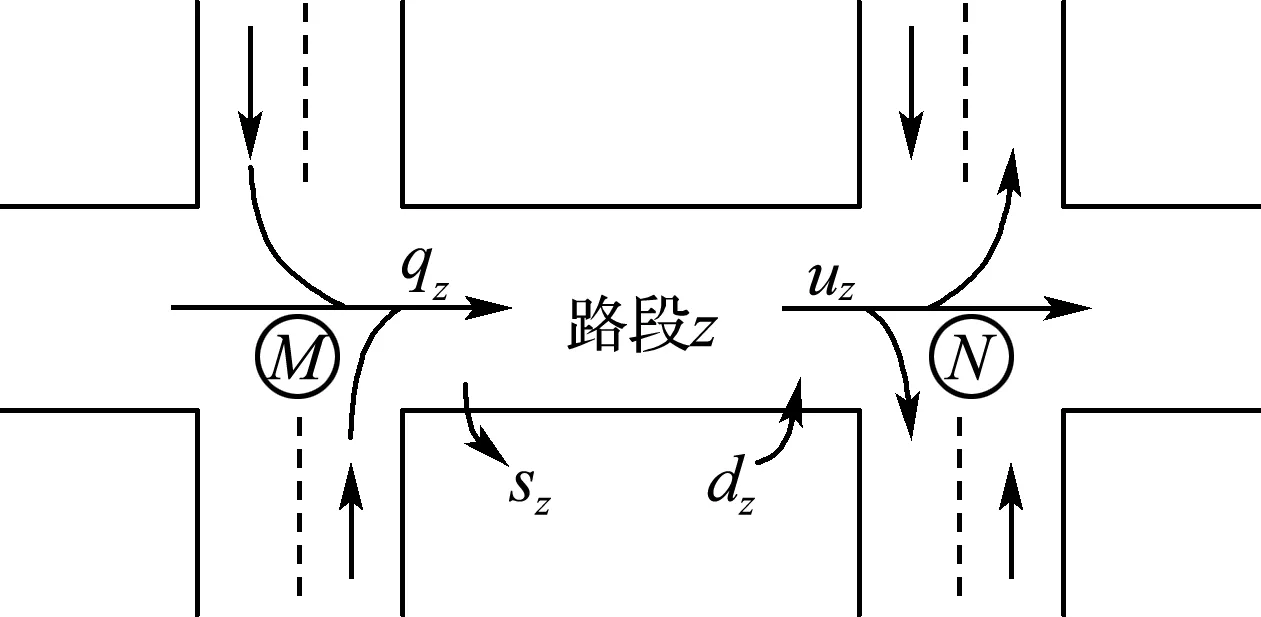
圖1 “存儲與向前”路段模型

根據圖1及表1可建立如下的路段模型：

xz(k+1)=xz(k)+T[qz(k)-sz(k)+

dz(k)-uz(k)]

(1)

其中

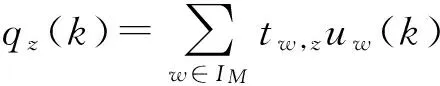
(2)

sz(k)=tz,oqz(k)

將式(2)代入式(1)，并令X(k+1)=(x1(k+1)x2(k+1) …xnx(k+1))T，即可得如下的城市路網拓撲模型：

X(k+1)=X(k)+BU(k)+d(k)

(3)

式中：X(k)=(x1(k)x2(k) …xnx(k))T，其中的各分量表示kT時刻含有nx條路段的路網系統中的各條路段中的車輛數；U(k)=(u1(k)u2(k) …unu(k))T，其中的各分量表示[kT,(k+1)T]期間路網系統中的全部路口信號燈的各相位綠燈時間占所在信號燈周期的百分比；矩陣B是由路段模型(1)推導得到的系數矩陣；列向量d(k) 的各元素分別表示[kT,(k+1)T]期間車輛從各路段中途駛入的平均流量．

在實際交通系統中，每個相位時間必須大于最短綠燈時間且小于最長綠燈時間，故控制變量U(k)具有以下約束條件：

uz,min≤uz(k)≤uz,max

(4)

其中uz,min、uz,max分別表示路段z中車輛有權通過路口的最短、最長相位時間占信號周期的百分比，uz,min可以為零，表示相應相位的綠燈時間為零，即出現全紅相位．另外，路口j的各相位綠燈時間百分比之和應滿足

(5)

式中：Lj表示路口j的黃燈時間之和；Cj表示路口j的信號周期；Pj表示路口j的相位數．

1.2 不確定模型

為了使得路網控制系統的控制效果達到一個穩態點，從而協調路網系統中各路段的交通狀況，首先給出如下定義：

ΔX=X-XN， ΔU=U-UN， Δd=d-dN

(6)

式中：XN表示狀態量X的名義值，即各路段的期望車隊長度；UN表示控制量U的名義值；dN表示d的名義值，并滿足d=dN，則Δd=0．由XN(k+1)=XN(k)得如下名義系統：

XN(k)=XN(k)+BUN+dN

(7)

由式(7)可知

BUN+dN=0

(8)

從而求解UN轉化為如下的求可行解問題：

BUN+dN=0

s.t.uz,min≤uz,N≤uz,max

(9)

結合式(3)和(7)可得如下狀態空間模型：

ΔX(k+1)=ΔX(k)+BΔU(k)

(10)

在實際交通狀況中，測量誤差、飽和流量的浮動等多種外界因素對交通流量的影響，將會導致交通模型具有不確定性，為此引入不確定矩陣，則式(10)可以轉換為

ΔX(k+1)=(I+ΔA(k))ΔX(k)+

(B+ΔB(k))ΔU(k)

(11)

其中ΔA(k)和ΔB(k)為不確定矩陣且滿足以下等式：

ΔA(k)=Δa(k)Fa=

(12)

ΔB(k)=EbΔb(k)Fb=

(13)

2 魯棒預測控制

針對具有不確定參數的城市路網模型(11)，采用基于LMI的魯棒預測控制方法，設計一個狀態反饋控制器調節每個路口各相位的綠燈時間，從而解決城市路網系統擁堵問題．在給出主要定理前，首先引入以下引理：

引理1[13]設W、M、N、G為具有適當維數的實矩陣，其中G滿足GTG≤I，W為對稱矩陣，那么

W+NTGTMT+MGN<0

(14)

當且僅當存在常數ε>0，使得

W+ε-1NTN+εMMT<0

2.1 無窮時域極小-極大問題

首先定義如下的無窮時域性能指標：

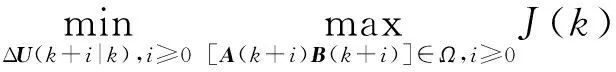
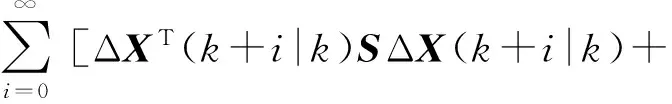
(15)

ΔUT(k+i|k)RΔU(k+i|k)]

式中：S和R為給定的對稱正定加權矩陣；ΔX(k)=ΔX(k|k)為kT時刻的狀態測量值；ΔX(k+i|k)為kT時刻對(k+i)T時刻的狀態預測值；ΔU(k+i|k)為kT時刻求得的(k+i)T時刻的最優控制輸入．

本文的目的是設計一個如下所示的無記憶狀態反饋控制器：

ΔU(k+i|k)=K(k)ΔX(k+i|k)

(16)

使得對所有允許的不確定性，閉環系統

ΔX(k+1)=[I+ΔA(k)+(B+

ΔB(k))K(k)]ΔX(k)

(17)

穩定．

定理1 對于閉環系統(17)，如果存在矩陣Q(k)、Y(k)以及常數ξ1(k)、ξ2(k)和γ(k)，使得以下優化問題

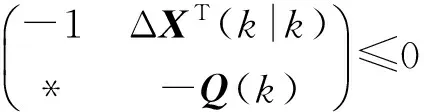
(18)

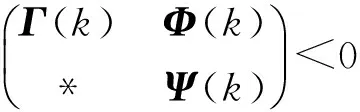
有解，則存在狀態反饋控制器(16)，使得閉環系統(17)漸近穩定．其中

H2(k)=Q(k)+BY(k)

狀態反饋控制器增益K(k)=Y(k)Q-1(k)．

證明 選取Lyapunov函數V(k)=ΔXT(k)·P(k)ΔX(k)，其中P(k)=PT(k)>0．若以下不等式

V(k+i+1|k)-V(k+i|k)≤

-[ΔXT(k+i|k)SΔX(k+i|k)+

ΔUT(k+i|k)RΔU(k+i|k)]

(19)

成立，則式(19)滿足Lyapunov穩定條件：

V(k+i+1|k)-V(k+i|k)≤0

(20)

從而可知閉環系統(17)漸近穩定．

將閉環系統(17)代入不等式(19)可得

LT(k)P(k)L(k)-P(k)+S+KT(k)RK(k)≤0

(21)

其中L(k)=I+ΔA(k)+BK(k)+ΔB(k)K(k)．

對式(21)應用Schur補定理可得

(22)

對式(22)依次應用引理1和Schur補定理可知，上式成立當且僅當存在常數ε1(k)>0和ε2(k)>0滿足

(23)

其中

對式(23)兩邊分別左乘、右乘矩陣diag{γ1/2(k)I,γ1/2(k)I,γ1/2(k)I,γ1/2(k)P-1(k),γ1/2(k)I,γ1/2(k)I,γ1/2(k)I}，并令Q(k)=γ(k)P-1(k)，Y(k)=γ(k)K(k)P-1(k),ξ1(k)=ε1(k)γ(k)，ξ2(k)=ε2(k)γ(k)，可得式(18)的條件2．

將式(19)兩邊從i=0到i=∞求和可得

J(k)≤V(k)

(24)

令Lyapunov函數的上界為γ(k)，則由上式可得

J(k)≤V(k)≤γ(k)

(25)

即求解性能指標J(k)的上界可轉化為求解V(k)的上界．由上式可得

V(k)=ΔXT(k)P(k)ΔX(k)≤γ(k)

(26)

對式(26)應用Schur補定理可得到式(18)的條件1．

2.2 約束處理

為了使用線性矩陣不等式處理方法處理魯棒預測控制，需要對約束(4)、(5)進行必要的處理．

首先，根據問題(9)求得UN后，式(4)、(5)的左右兩邊分別減去控制變量的名義值UN，并令uz,min=0，每個路口的信號周期均為C，則式(4)、(5)可轉換為

-uz,N≤Δuz(k+i|k)≤uz,max-uz,N

(27)

(28)

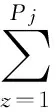
首先，對約束(27)作如下處理：

(29)

其中

(30)

進而將式(30)轉換為以下線性矩陣不等式：

(31)

同理，可將約束(28)轉換為

(32)

由式(32)可得如下線性矩陣不等式：

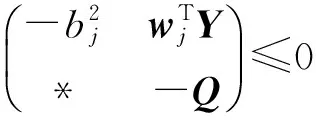
(33)

2.3 魯棒預測控制算法

對城市路網采用魯棒控制策略，能有效處理由測量誤差、飽和流量的浮動等引起的交通狀態的不確定性．本文提出的魯棒預測控制算法步驟具體如下：

步驟1 在控制算法迭代初始時刻，設k=0,K=0．

步驟2 算法迭代開始，采集kT時刻的狀態量，并在線求解優化問題(18)、(31)、(33)，得到最優解Q(k)、Y(k)，進而得到控制器增益

K(k)=Y(k)Q(k)

步驟3 求解得到控制量ΔU(k)=K(k)·ΔX(k)．

步驟4 進入下一采樣時刻，令k=k+1，返回步驟2．

3 仿真與實現

在仿真與實現中，考慮采用包含4個路口的路網系統，如圖2所示．

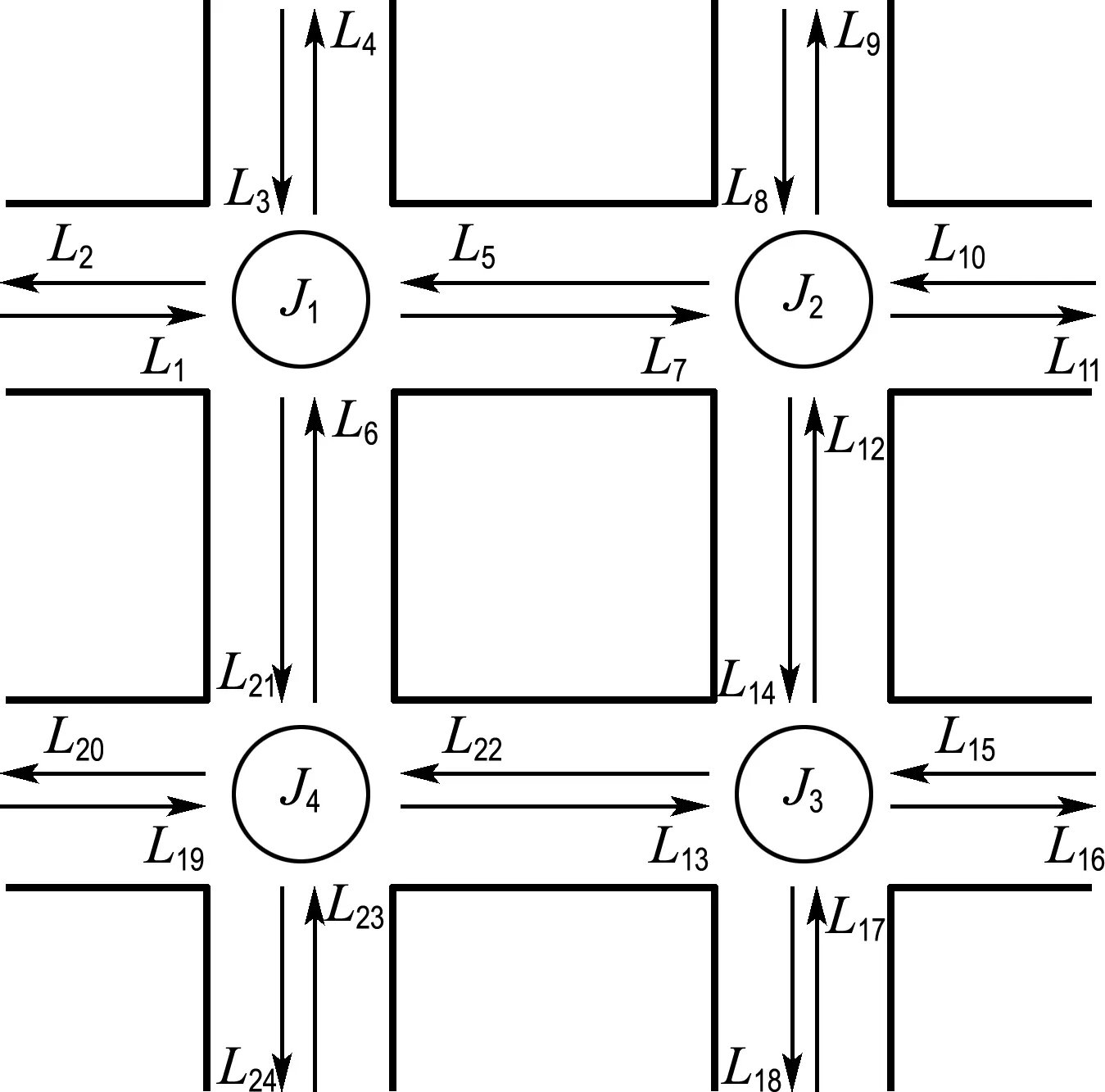
圖2 4個路口的路網系統

該路網系統共包含24條車道{L1,L2,…,L24}，但是受控的車道只有{L1,L3,L5,L6,L7,L8,L10,L12,L13,L14,L15,L17,L19,L21,L22,L23}．各車道的轉彎率如下：t1,4=0.05，t1,21=0.15，t3,2=0.12，t3,7=0.20，

t5,4=0.05，t5,21=0.15，t6,2=0.12，t6,7=0.20，

t7,9=0.05，t7,14=0.15，t8,5=0.20，t8,11=0.12，

t10,9=0.15，t10,14=0.15，t12,5=0.20，t12,11=0.12，

t13,12=0.15，t13,18=0.05，t14,22=0.20，t14,16=0.12，

t15,12=0.15，t15,18=0.10，t17,22=0.20，t17,16=0.12，

t19,6=0.15，t19,24=0.15，t21,20=0.12，t21,13=0.20，

t22,6=0.15，t22,24=0.05，t23,20=0.12，t23,13=0.20定義p=ST，且

p1=40，p3=50，p5=50，p6=50;

p7=45，p8=50，p10=50，p12=50;

p13=50，p14=50，p15=50，p17=50;

p19=50，p21=50，p22=50，p23=50

每個路口的信號燈周期均為C=120 s，其中，黃燈損失時間為L1=L2=L3=L4=16 s，每個周期含有4個相位，如圖3所示．

圖3 路口的相位示意圖

名義系統的XN和dN分別為

XN=(25 25 20 20 20 25 25 20

20 20 25 25 25 20 20 25)T

dN=(9 9 0 0 0 9 9 0 0 0

9 9 9 0 0 9)T

根據式(9)可求解得UN．選取加權矩陣S=I，R=1 000I．采用魯棒預測控制方法，設計控制器調節路口信號燈，使得路口車隊長度趨于期望值，從而緩解交通擁堵．

對比圖5中(a)、(b)可知，在無控制情況下，J1路口的各車隊長度逐漸變長，導致交通擁堵狀況惡化；采用本文提出的具有輸入約束的狀態反饋控制器，J1路口的車道L1、L3和L6中的車隊長度經過多個信號周期的控制調整后趨于期望的車隊長度，防止了擁堵狀況的惡化，有效緩解了路口的擁堵狀況．

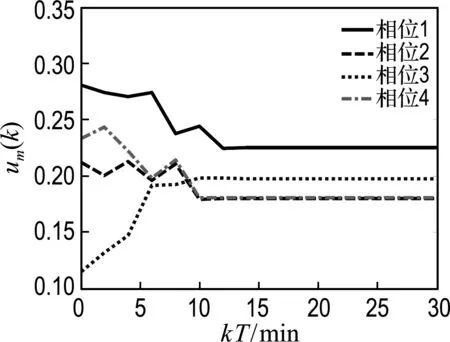
圖4 路口J1的控制輸入

(a) 魯棒預測控制

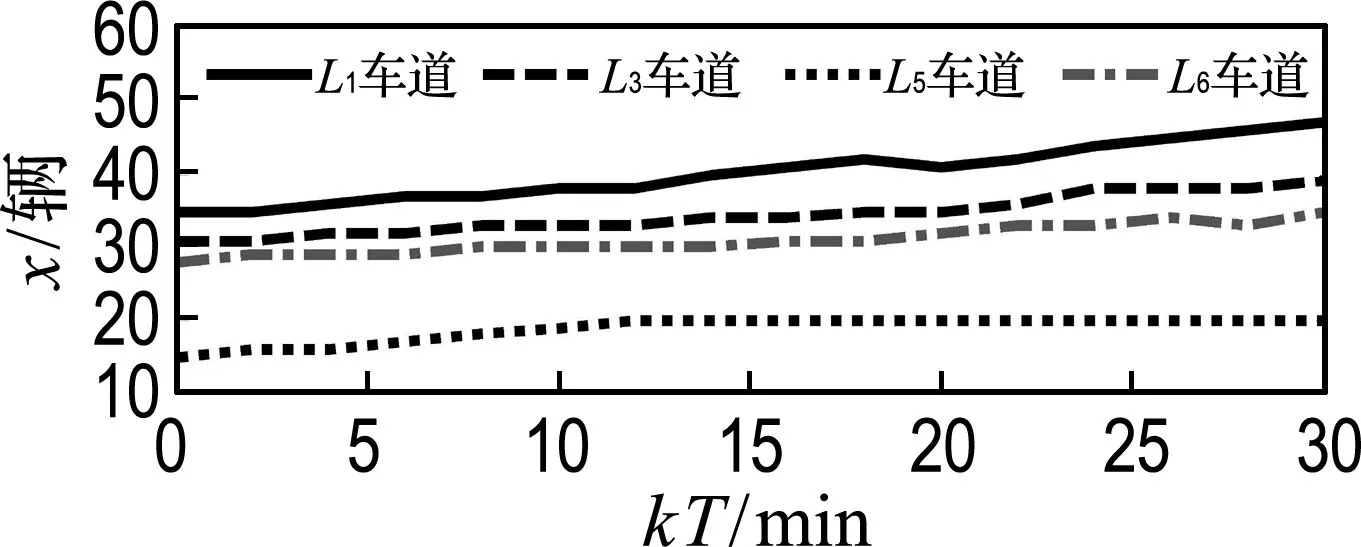
(b) 無控制

圖5 路口J1的狀態軌跡

Fig.5 State trajectory of intersectionJ1

4 結 語

本文將“存儲與向前”路段模型改進為具有不確定性的路網系統模型，并且使得輸入量滿足一定的約束條件，采用魯棒預測控制方法解決了帶有約束的凸優化問題．仿真研究表明：系統滿足約束條件，具有較強的魯棒性，能有效協調路網系統中的交通狀況．

[1] Papageorgiou M, Diakaki C, Dinopoulou V,etal. Review of road traffic control strategies [J]. Proceedings of the IEEE, 2003, 91(12):2043-2065.

[2] Bruno G, Improta G. Urban traffic control:current methodologies [M] // Artificial Intelligence Applications to Traffic Engineering. Zeist:VSP International Science Publishers, 1994:69-93.

[3] Burger M, Van Den Berg M, Hegyi A,etal. Considerations for model-based traffic control [J]. Transportation Research Part C:Emerging Technologies, 2013, 35:1-19.

[4] Daganzo C F. Cell transmission model:a dynamic representation of highway traffic consistent with the hydrodynamic theory [J]. Transportation Research Part B:Methodological, 1994, 28(4):269-287.

[5] Diakaki C, Papageorgiou M, Aboudolas K. A multivariable regulator approach to traffic-responsive network-wide signal control [J]. Control Engineering Practice, 2002, 10(2):183-195.

[6] Aboudolas K, Papageorgiou M, Kosmatopoulos E. Store-and-forward based methods for the signal control problem in large-scale congested urban road networks [J]. Transportation Research Part C:Emerging Technologies, 2009, 17(2):163-174.

[7] De Souza F A, Peccin V B, Camponogara E. Distributed model predictive control applied to urban traffic networks:Implementation, experimentation, and analysis [C] // 2010 IEEE International Conference on Automation Science and Engineering, CASE 2010. Piscataway:IEEE Robotics and Automation Society, 2010:399-405.

[8] De Oliveira L B, Camponogara E. Multi-agent model predictive control of signaling split in urban traffic networks [J]. Transportation Research Part C:Emerging Technologies, 2010, 18(1):120-139.

[9] LIN Shu, De Schutter B, XI Yu-geng,etal. Efficient network-wide model-based predictive control for urban traffic networks [J]. Transportation Research Part C:Emerging Technologies, 2012, 24:122-140.

[10] Ng K M, Reaz M B I, Ali M A M. A review on the applications of petri nets in modeling, analysis, and control of urban traffic [J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2):858-870.

[11] Le T, Vu H L, Nazarathy Y,etal. Linear-quadratic model predictive control for urban traffic networks [J]. Transportation Research Part C:Emerging Technologies, 2013, 36:498-512.

[12] Wakasa Y, Iwaoka K, Tanaka K. Modelling and robust control of traffic signal systems [C] // European Control Conference, ECC 2003. Piscataway:IEEE, 2003:1928-1933.

[13] 樊衛華,蔡 驊,陳慶偉,等. 時延網絡控制系統的穩定性[J]. 控制理論與應用, 2004, 21(6):880-884. FAN Wei-hua, CAI Hua, CHEN Qing-wei,etal. Stability of networked control systems with time-delay [J]. Control Theory & Applications, 2004, 21(6):880-884. (in Chinese)

Robust predictive control for urban road network

LIU An-dong*, LI Jia, YU Li

( College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China )

For urban road network system with model uncertainty, a robust predictive state feedback controller is designed to ensure the closed-loop system asymptotically stable. Firstly, the store-and-forward segment linear model is extended to the urban road network topology model. Considering the influence of saturation flow rate and vehicle number uncertainty caused by the road conditions change and the error of measurement, the urban road network system model with parameters uncertainty is proposed. Furthermore, a convex optimization problem with constraints is solved by linear matrix inequality (LMI) treatment to design the state feedback controller. Finally, the effectiveness of the proposed method to alleviate the urban traffic congestion and optimize the signal lights is demonstrated by Matlab simulation.

robust predictive control; urban road network system; parameter uncertainty; linear matrix inequality (LMI)

1000-8608(2016)02-0202-06

2015-10-05；

2015-11-19．

國家自然科學基金資助項目(61273117,61403344).

劉安東*(1985-)，男，博士，講師，E-mail:lad@zjut.edu.cn.

TP273

A

10.7511/dllgxb201602014