基于中心差分卡爾曼濾波的初始對準方法研究

賈鶴鳴，楊澤文，宋文龍

(東北林業(yè)大學 機電工程學院，哈爾濱 150040)

?

基于中心差分卡爾曼濾波的初始對準方法研究

賈鶴鳴，楊澤文，宋文龍*

(東北林業(yè)大學 機電工程學院，哈爾濱 150040)

由于建立的大方位失準角下的捷聯(lián)慣性導航系統(tǒng)誤差模型具有非線性的特點，本文選用中心差分卡爾曼濾波(CDKF)方法對捷聯(lián)慣導系統(tǒng)的控制對象進行初始對準仿真。并與無跡卡爾曼濾波(UKF)和擴展卡爾曼濾波(EKF)兩種濾波方式進行比較，最后得出CDKF可以提高系統(tǒng)的圖像和目標的濾波精度的結(jié)論，并且不需要具體模型計算出解析方程，節(jié)約了計算復雜的具有驅(qū)動約束方程的雅可比(Jacobian)矩陣的時間。最后的仿真結(jié)果證明CDKF對系統(tǒng)狀態(tài)進行最優(yōu)估計的算法明顯優(yōu)于EKF和UKF，同時具有較高的精度和收斂性，能夠滿足在非線性模型下的系統(tǒng)對導航的要求。

大方位失準角；捷聯(lián)慣導；初始對準；CDKF

0 引 言

SINS(捷聯(lián)慣性導航系統(tǒng))中所不可或缺的一項技術是初始對準，在初始對準過程中的控制精度和所用時間會影響到整個系統(tǒng)的工作靜態(tài)和動態(tài)性能[1-5]。擴展卡爾曼濾波(EKF)方法在失準角誤差模型的非線性系統(tǒng)應用很多[6-7]，然而這種濾波方法存在精確度和準確性的缺點，例如在將非線性方程問題變成線性方程問題來的求解過程中，通常會忽略泰勒級數(shù)展開式中部分的高階項，因此造成EKF濾波方式出現(xiàn)了較大的線性化誤差，從而降低濾波精度甚至會使結(jié)果發(fā)散，造成工作狀態(tài)難以穩(wěn)定，并且推導具有驅(qū)動約束方程的雅可比(Jacobian)矩陣需要的時間長，因此在實際中很難廣泛應用。

針對EKF的不足，近年來人們提出了Sigma點卡爾曼濾波(SPKF)方法，其分析系統(tǒng)的性能較EKF比有較大的改善。SPKF主要分為兩種，一種是中心差分卡爾曼濾波(CDKF)，另一種是無跡卡爾曼濾波(UKF)。 CDKF 最早由ITO[8]和Norgaard[9]等人提出，他們基于卡爾曼在NASA埃姆斯研究中心時產(chǎn)生靈感發(fā)現(xiàn)的濾波方法，使CDKF避開了EKF濾波時需要被控系統(tǒng)模型計算出具體解析方程的劣勢，并能隔離隨機變量噪聲，具有較低的線性化誤差和高定位準確度的優(yōu)點。另外，CDKF比 UKF的理論精度高。因此CDKF方法在目前導航、航空領域中有諸多的應用，效果也十分完善。

本文首先介紹了中心差分卡爾曼濾波的原理，然后從基于歐拉平臺誤差角描述實際地理坐標系再到分析其與計算地理坐標系的變換關系，最后創(chuàng)建一個SINS在失準角為大方位條件下的非線性模型；研究CDKF在SINS大方位失準角初始對準條件下濾波效果。本文分別利用了EKF、UKF和CDKF三種方法進行了仿真驗證并進行比較，仿真結(jié)果進一步證明了中心差分卡爾曼濾波(CDKF)方法顯著優(yōu)于EKF和UKF。是一種更為優(yōu)越，實用性強的非線性濾波方法。

1 SINS大方位失準角初始對準誤差模型

上者的轉(zhuǎn)移關系可用以下列矩陣來表示：

(1)

(2)

(3)

(4)

當φx，φy很小時cosφx=cosφy=1，sinφx≈φx，sinφy≈φy，則

(5)

(6)

1.1 速度誤差方程

理論上，SINS的速度微分方程表示為：

(7)

不忽略外界干擾情況下，SINS的速度微分方程為：

(8)

(9)

1.2 姿態(tài)角誤差方程

(10)

(11)

失準角運動方程為：

(12)

(13)

(14)

(15)

1.3 建立非線性捷聯(lián)慣性導航系統(tǒng)初始對準模型

假設計算出的陀螺儀的誤差漂移εb是一個恒定值；加速度計的誤差是恒定值零偏b；假定在靜基座快速初始對準條件下，所在位置是恒定不變的且已知的，此刻滿足=[0 ωiecosL ωiesinL]Tvt=0；其中R為地球半徑，L為緯度，忽略重力誤差項δgt以及不考慮δvz，則可得狀態(tài)方程為：

(16)

令狀態(tài)向量X為：

用捷聯(lián)慣性導航系統(tǒng)兩程度速度誤差X=δVt作為觀測誤差并測量，建立非線性對準模型：

(17)

其中，f(X)的表達式可以參考公式(16)進行表示，G是10×5維的矩陣系數(shù)，G(1,1)=G(2,2)=G(3,3)=G(4,4)=G(5,5)=1，H代表量測矩陣H=[02×3∶I2×2∶02×5]，V代表量測噪聲。

2 基于CDKF的狀態(tài)估計

2.1 中心差分變換 中心差分變換是研究在SINS在失準角為大方位條件下中心差分卡爾曼濾波濾波器的基礎，同時它也是一種以插值理論為基礎的高效的非線性變換方法，是SPKF的一種，可以用來求解經(jīng)過非線性變換后的一些統(tǒng)計學量，例如均值和方差。研究CDKF的切入點是借助sterling差值定理，進而求取逼近多項式非線性方程的導數(shù)，節(jié)約了進行復雜求導運算的時間，它運用了中心差分方法代替泰勒展開式中指數(shù)為1和2[10]。

y=f(x)。

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

其中Sxi表示柯勒斯基(cholesky)分解中Sx的第i列。

2.2 中心差分卡爾曼濾波方法研究

CDKF雖然表達形式與EKF類似，實際上卻是利用先驗分布構(gòu)造一組確定性采樣點 Sigma 點，充分考慮了高斯隨機變量的統(tǒng)計特性[13-14]，并用經(jīng)過線性回歸變換后得到的Sigma(一組確定性采樣點)來表示實驗狀態(tài)的后驗分布。針對非線性濾波的難題[15-16]CDKF 采用了中心差分變換方法，并且發(fā)現(xiàn)CDKF較傳統(tǒng)EKF算法具有濾波精度高，過程較穩(wěn)定的優(yōu)點，且不需要計算具有約束方程的Jacobian；節(jié)約了大量的時間，而與UKF濾波算法相比較，其又具有精度高，對狀態(tài)協(xié)方差敏感性要低的優(yōu)點。同時，在CDKF中，當出現(xiàn)系統(tǒng)測量噪聲和系統(tǒng)本身自有噪聲均為復雜加性噪聲的情況時，為了減輕濾波計算，可不進行狀態(tài)增廣。由此可見，CDKF與上面兩種濾波算法相比而言，在處理SINS大方位失準角初態(tài)對準方面問題中具有相當明顯的優(yōu)勢。

設非線性系統(tǒng)為：

(28)

其中，k時刻的狀態(tài)向量為xk，觀察向量用yk，wk和vk為兩兩互不關聯(lián)的均值為0的高斯噪聲。針對上述非線性模型，利用中心差分變換方法進行狀態(tài)估計，推導出中心差分卡爾曼濾波的算法[17]如下：

(1)初始化

(29)

(30)

(2)確定權值

(31)

(32)

(3)確定sigma點集

(33)

(4)時間更新

(34)

(35)

(36)

(5)sigma點更新

(37)

(6)量測更新

yk/k-1=h(χk/k-1)。

(38)

(39)

(40)

(41)

(42)

(43)

(44)

3 仿真研究

3.1 仿真條件

在靜基座初始對準狀態(tài)下，假定當前的初態(tài)失準角度φx=φy=0.6°，φz=10°；陀螺儀常值漂移為0.02°/h；隨機漂移為0.01°/h；加速度計零偏為100 μg；隨機偏差為50 μg；速度測量誤差為0.1 m/s；當?shù)氐乩砭暥葹?5.779 6°，則P(0)、Q、R可表示為：

P(0)=diag{(0.6°)2,(0.6°)2,(10°)2,(0.1 m/s)2,(0.1 m/s)2,(0.02°/h)2,(0.02°/h)2,(0.02°/h)2,(100 μg)2,(100 μg)2}

Q=diag{(0.01°/h)2,(0.01°/h)2,(0.01°/h)2,(50 μg)2,(50 μg)2,0,0,0,0,0}

R=diag{(0.1 m/s)2,(0.1 m/s)2}。

得到上述仿真條件，分別采用擴展卡爾曼濾波器(EKF)、無損卡爾曼濾波(UKF)和中心差分卡爾曼濾波(CDKF)三種方法對系統(tǒng)進行濾波仿真比較，仿真時間均設定為300 s。

3.2 仿真結(jié)果分析

失準角估計誤差的對比情況見表1。系統(tǒng)的仿真結(jié)果如圖1和圖2所示。

表1 大方位失準角的估計誤差Tab.1 Estimation error of large azimuth misalignment

因為北向和東向的水平失準角仿真估計結(jié)果類似，所以圖中只列出了系統(tǒng)中北向估計的結(jié)果。從北向水平失準角的曲線圖和大方位失準角的誤差表很容易得出，每個濾波算法對在兩方向失準角條件下的仿真結(jié)論基本相當，收斂速度都很快，均能得到很好很穩(wěn)定的濾波結(jié)果。從圖2和表1得出，UKF和CDKF兩者對大方位失準角的估計，收斂速度、時變系統(tǒng)跟蹤速度與收斂精度優(yōu)于EKF，首要原因是 EKF在線性化濾波過程中存在一階截斷問題，會產(chǎn)生截斷誤差，造成方位失準角誤差的急劇增大，而UKF因為算法中存在二階截斷問題，會使方位失準角誤差增加的更快，所以效果也不如CDKF。CDKF與UKF相比，CDKF具有在相同增長時，接近穩(wěn)定值的速度較快和濾波精度高的特點。因此CDKF在三種濾波方式中擁有相當顯著實用的優(yōu)點。

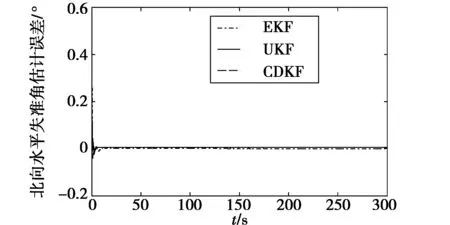
圖1 北向水平失準角的誤差曲線Fig.1 Estimation error curves of north misalignment

圖2 天向失準角預計的誤差曲線Fig.2 Estimation error curves of azimuth misalignment

4 結(jié) 論

本文內(nèi)容深入研究CDKF濾波，并在SINS大方位失準角初始對準中得到了廣泛的應用，利用其具有精度高，穩(wěn)定性好的優(yōu)點，有效解決了復雜的誤差模型具有的非線性問題。以上仿真出的圖形和表格表現(xiàn)出CDKF比EKF具有更高濾波精度，同時節(jié)約了求解復雜的雅可比矩陣的時間，提高了系統(tǒng)可靠性，這些優(yōu)點都將是CDKF成為更主流濾波方法的重要因素。CDKF與UKF相比，CDKF不但具有濾波精度高和保證收斂速度比較快的特點，同時減少了工作量，使數(shù)值的穩(wěn)定程度提高。仿真結(jié)果證實了CDKF的確在基于中心差分卡爾曼濾波對大方位失準角初始對準問題中較其他仿真方法而言優(yōu)越性非常的顯著，實現(xiàn)功能更加容易便捷，實際應用愈加廣泛，是一種研究非線性系統(tǒng)濾波十分高效的算法。

[1]Ito K，Xiong K.Gaussian filters for nonlinear filtering problems[J].IEEE Transactions on Automatic Control，2000,45(5)：910-927.

[2]N?rgaard M，Poulsen N K，Ravn O.Advances in derivative-free state estimation for nonlinear systems[R].Informatics and Mathematical Modelling，Technical University of Denmark，DTU，1998.

[3]劉國海，李康吉.基于PDA的GPS定位精度提高方法[J].江蘇大學學報：自然科學版.2005，26(5)：448-452.

[4]Norgaard M，Pouisen N K，Ravn O.New Developments in State Estimation for Nonlinear System[J]．Automatica，2000，36(11)：1627-1638.

[5]Van Der Merwe R.Sigma-point Kalman filters for probabilistic inference in dynamic state-space models[D].Oreg：Oregon Health & Science University，2004.

[6]王海勃，陳紅林，韓惠珍.CDKF在GPS/SINS組合導航系統(tǒng)非線性模型中的應用[J].現(xiàn)在電子技術，2011，34(11)：19-23.

[7]龍 瑞，秦永元，夏家和.CDKF在捷聯(lián)慣導系統(tǒng)大失準角初始對準的應用[J].西北工業(yè)大學學報，2010，28(3)：364-368.

[8]嚴恭敏，嚴衛(wèi)生，徐德民.簡化UKF濾波在SINS大失準角初始對準中的應用[J].中國慣性技術學報，2008，16(3)：253-264.

[9]黃鳳榮，孫偉強，翁海娜.基于UKF的旋轉(zhuǎn)式SINS大方位失準角初始對準方法[J].中國慣性技術學報，2010，18(5)：513-517.

[10]Gao W，Xu B，Sun H，et al.Application of nonlinear filtering for SINS initial alignment[C].2006 International Conference on Mechatronics and Automation.IEEE，2006：2259-2263.

[11]孫 楓，唐李軍.Cubature卡爾曼濾波-卡爾曼濾波算法[J].控制與決策，2012，27(10)：1561-1565.

[12]趙 奇.卡爾曼濾波在GPS定位中的研究與實現(xiàn)[D].成都：電子科技大學.2013.

[13]錢華明，葛 磊，彭 宇.多漸消因子卡爾曼濾波及其在SINS初始對準中的應用[J].中國慣性技術學報，2012，20(3)：287-291.

[14]楊 丹.卡爾曼濾波器設計及其應用研究[D].湘潭：湘潭大學.2014.

[15]杜黨波，張 偉，胡昌華，等.含缺失數(shù)據(jù)的小波-卡爾曼濾波故障預測方法[J].自動化學報，2014，40(10)：2115-2125.

[16]韓 萍，桑威林，石慶研.一種新型非線性卡爾曼濾波方法[J].儀器儀表學報，2015，36(3)：632-638.

[17]李方能，許江寧，亓洪標 基于邊緣采樣UKF濾波的捷聯(lián)慣導初始對準方法[J].中國慣性技術學報，2014，22(5)：612-618.

Study on Initial Alignment Method Basedon Central Difference Calman Filter

Jia Heming ，Yang Zewen，Song Wenlong*

(College of Mechanical and Electrical Engineering，Northeast Forestry University，Heilongjiang，Harbin 150040，China)

Because the error model of the strapdown inertial navigation system is of nonlinear characteristics under the established large azimuth misalignment，the Central Difference Kalman Filter (CDKF) method was used to conduct the initial alignment simulation for controlling object of the strapdown inertial navigation system in this paper.Compared with the extended Kalman filter (EKF) and the unscented Kalman filter (UKF)，CDKF would improve the filtering precision of the system image and the objective，and did not need specific models to calculate the analytical equation，which saved the time for computing Jacobian matrix of driven complex constraint equations.The final simulation results demonstrated that the use of CDKF for the optimal estimation of system sate was better than EKF and UKF methods，the CDKF algorithm was of the high precision and convergence and could satisfy the system requirements for navigation under the nonlinear model.

Large azimuth misalignment；strapdown inertial navigation system；initial alignment；CDKF

2016-03-08

中央高校基本科研業(yè)務費專項資金資助項目(2572014BB03)；國家自然科學基金(31470714)

賈鶴鳴，博士，副教授。研究方向：非線性系統(tǒng)控制理論與應用、智能控制與濾波技術。

*通信作者：宋文龍，博導，教授。研究方向：控制系統(tǒng)的檢測與濾波技術。E-mail：wlsong@126.com

賈鶴鳴，楊澤文，宋文龍.基于中心差分卡爾曼濾波的初始對準方法研究[J].森林工程，2016，32(6)：66-70.

TP 273

A

1001-005X(2016)06-0066-05