混合動力汽車用內置永磁同步電動機參數估計方法研究

馬建偉，梁曉琳，張鵬飛

(邢臺職業技術學院，邢臺 054000)

?

混合動力汽車用內置永磁同步電動機參數估計方法研究

馬建偉，梁曉琳，張鵬飛

(邢臺職業技術學院，邢臺 054000)

內置式永磁同步電機具有恒功率范圍寬、功率密度大、效率高等特點，因此其在混合動力汽車中的應用比較廣泛。由于混合動力汽車用電機工作環境惡劣、負載突變大，且內置式永磁同步電機的參數易受溫度、磁飽和等因素的影響，大大降低了其控制性能。針對電機的精確控制，首先建立了前置永磁同步電機的數學模型；電機轉矩主要與磁鏈和d，q軸電感差值有關，故針對電機磁鏈和電感進行在線估計。提出了一種基于前饋式電流解耦的磁鏈估計算法，能夠很好地消除工況變化對電機的影響；同時提出了一種基于功率閉環的d，q軸電感差值估計算法，可實現電機的精確控制。仿真和實驗驗證了所述參數估計方法的有效性。

內置永磁同步電機；磁鏈估計；混合動力汽車

0 引 言

當前汽車技術發展的主要方向在于新能源的利用，即新能源汽車。作為新能源汽車的主要形式，混合動力汽車的發展十分迅速。為保證混合動力汽車整車性能，驅動電機應具有高效、快速、準確和高可靠性等特點[1-5]。目前，混合動力汽車的驅動電機大多采用內置式永磁同步電動機(IPMSM)，實現電機的最優控制是保證整車性能的關鍵[6-7]。電機最優控制，主要在于兩個方面：電機參數的實時估計和適應參數變化的控制算法，如此可以提高系統的魯棒性。眾所周知，電機參數隨運行工況和環境會不停變化，例如永磁磁鏈、d，q軸電感等[8-9]。為解決此問題，國內外學者針對電機參數估計和相關控制算法展開了一些研究。

Morimoto S等人通過具體實驗測量發現隨著d，q軸電流的變化，d軸電感基本不會發生變化；而q軸電感會隨著q軸電流的增大而減小；因此在控制過程中可認為d軸電感為常數并用線性方程描述q軸電感和電流之間的關系；但是并沒有考慮d，q軸之間的交叉耦合效應，所以線性擬合是不夠準確的[10]。

Qi G等人則考慮了交叉耦合效應，基于二維有限元法對d，q軸電感進行預測，并采用 MAP插值法對得到的d，q軸電感進行優化；但是該方法花費巨大而且無法滿足所有工況，即在特殊工況下會出現較大偏差，無法實現最優控制[11]。

Boileau T等人分析了電機參數與電機穩態方程之間的關系，認為穩定工況下無法實現所有參數的識別，因此需要將部分參數假定為已知參數。另外，若要識別所有參數，需要采用信號注入等方法或增加傳感器數量，上述方法并不適用于車用永磁同步電動機[12]。

哈爾濱工業大學鄭維以及清華大學田碩等人將輸出轉矩實際值和參考值之間的關系制作成二維或三維表格(Map)，并存儲在控制器內部，進而實現電機的精確控制。但是該方法存在一定的局限性：涉及參數較少，難以應對復雜的工況；涉及參數較多，會增加混合動力系統匹配的工作量[13-14]。

針對上述問題，本文建立永磁同步電機模型，提出參數的估計算法，并將參數估計與變參數控制算法相結合，通過仿真和實驗證明了算法的有效性。

1 內置永磁同步電機數學模型

為便于分析和控制，可在d，q坐標系下，建立內置式永磁同步電動機電氣數學模型，如圖1所示。模型中繞組電阻rs可用于表示銅耗；鐵耗電阻rc可用于表示鐵耗；由于機械損耗與電氣參數無關，另外雜散損耗難以在模型中具體表示，所以該模型不考慮機械損耗和雜散損耗。

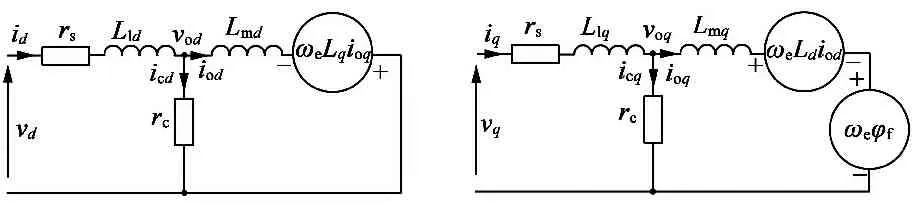
圖1 內置式永磁同步電機電氣數學模型

根據圖1中所示的內置式永磁同步電機電氣數學模型，其電氣方程可具體表示：

(1)

(2)

(3)

(4)

式中:vd和vq分別表示d軸和q軸相電壓；rs為繞組電阻；id和iq分別表示d軸和q軸總電流；Lld和Llq分別表示d軸和q軸漏電感；Lmd和Lmq分別表示d軸和q軸磁化電感；icd和icq分別表示d軸和q軸鐵耗電流；iod和ioq分別表示d軸和q軸總電流與鐵耗電流的差值；Ld和Lq分別表示d軸和q軸總電感；ωe為電角速度；φf為永磁磁鏈；rc為鐵耗電阻。

另外，永磁同步電機的轉矩和機械方程可分別表示：

(5)

(6)

(7)

式中:Te為電機電磁轉矩；p為電機極對數；Jm為轉子轉動慣量；TL為負載轉矩；TMec為風阻和摩擦轉矩；ωr為轉子角速度；θr為轉子位置。

若不考慮電流瞬態變化，那么穩態工況下的電機模型可描述：

(8)

(9)

(10)

(11)

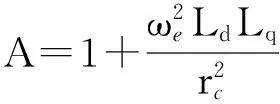
(12)

電機鐵耗可表示：

(13)

式中:φd和φq分別表示d軸和q軸磁鏈；Kh為電機磁滯損耗常數；Kf為電機渦流損耗常數；雜散損耗可表示：

(14)

式中:CStr為雜散損耗系數。機械損耗可表示：

(15)

式中:Bm為粘性摩擦系數；Tfric為摩擦轉矩。

2 內置式永磁同步電機參數估計

由前文分析可知，內置式永磁同步電機參數較多，其中等效鐵耗電阻、機械損耗系數、雜散電阻可通過測量獲得。相對而言，電機的磁鏈和電感變化較大且建模比較困難；與d軸相比，q軸電感受磁飽和等因素的影響要明顯。因此，本文以永磁磁鏈和q軸電感為例，進行在線估計。

2.1 磁鏈估計

由式(1)～式(4)可知，電機電壓和電流相互耦合，為保證電流控制的精確性，需要對d，q軸解耦。基于電機數學模型，其電壓傳遞函數可表示：

(16)

式(16)中最后一項為反向電動勢，可通過解耦控制消除。具有前饋解耦功能的永磁同步電機電流環控制[15]如圖2所示。

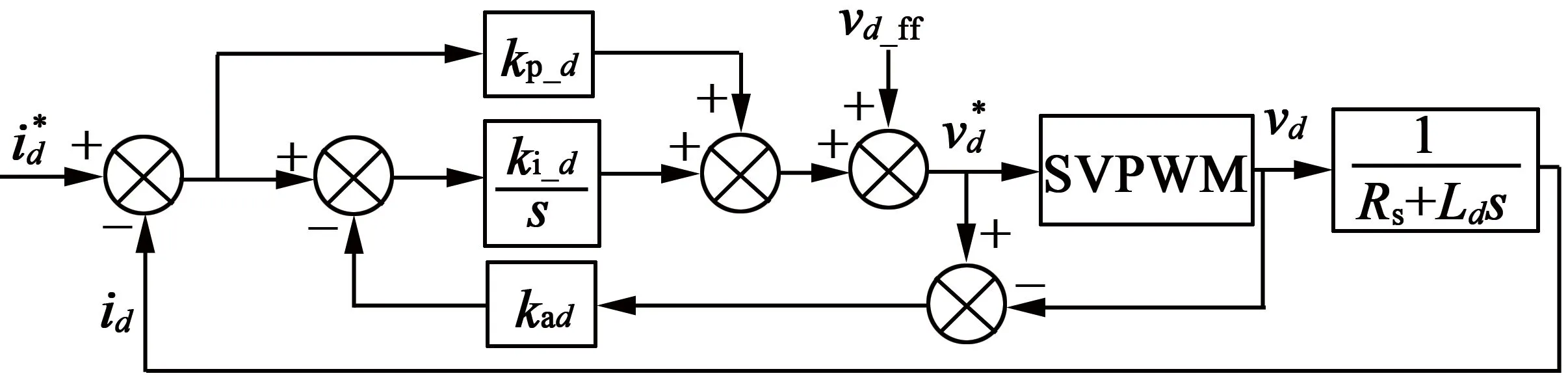
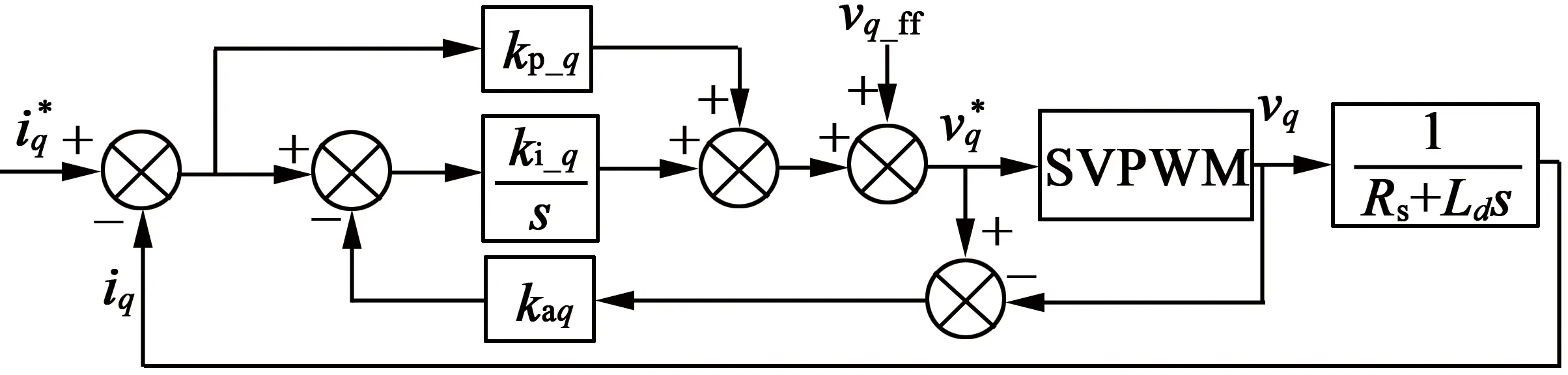
圖2 前置永磁同步電機電流環控制框圖

圖2中的解耦控制電壓可表示：

(17)

若PI電流控制器的輸出值為vd_fb和vq_fb，則上述帶前饋解耦電壓補償的電流環輸出電壓可表示：

(18)

在穩定工況下，電流環輸出電流值能夠較好地跟隨參考電流值，因此可忽略式(16)中的微分項，由式(16)～式(18)可得：

(19)

由式(18)和式(19)可得：

(20)

由式(20)可知，PI電流控制器的輸出值包括定子電阻壓降和磁鏈估計誤差。假設定子電阻的變化較小，可以忽略不計，那么可由電流環PI控制器的積分項得到磁鏈估計信息，即：

(21)

式中:vd_fb_i和vq_fb_i為電流環 PI 控制器的積分項；Δφd和Δφq為磁鏈誤差，可表示成實際值和估計值之間的差值。

綜上所述，前置永磁同步電機磁鏈估計算法可描述：

(22)

2.2 估計

(23)

此時參考轉矩輸出功率可表示：

(24)

在前述電流閉環控制下，實際輸出電流id和iq可認為與參考電流相等，即：

(25)

另外，電機實際轉矩功率：

(26)

假定交直軸電感實際差值為ΔL，交直軸電感理論差值為ΔL′。如果ΔL=ΔL′，則表示輸出轉矩實際值等于輸出轉矩參考值，轉矩輸出功率實際值等于轉矩輸出功率參考值；但是如果ΔL≠ΔL′，則表示輸出轉矩和轉矩輸出功率的實際值和參考值之間存在偏差。

將式(23)代入式(24)可得：

(27)

將式(27)對ΔL求偏導，可得：

(28)

一般情況下，混合動力車用電機可能處于電動機模式或發電機模式，即ioq數值可正或可負。鑒于內置式永磁同步電機的ΔL恒大于零，那么對(28)兩邊取絕對值，則有：

(29)

通過分析式(25)可知，ΔL偏差與功率偏差絕對值之間存在單調關系，所以ΔL的優化可以通過消除功率參考數值與功率實際輸出數值之間的偏差來實現。在磁鏈估計和dL估計的基礎上，基于最大轉矩比電流算法，可以實現變參數的在線估計和控制，進而滿足系統優化的需求，控制框圖如圖3所示。

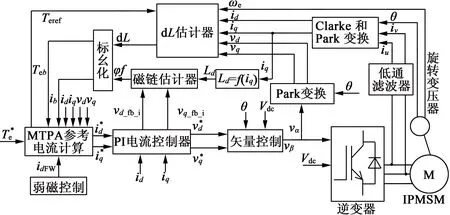
圖3 基于參數估計的變參數MTPA控制框圖

3 仿真分析和實驗驗證

為驗證上述參數估計方法的有效性，分別在額定工況(2000r/min,358N·m)和最大轉矩工況(1 000 r/min,540 N·m)下，對本文所提出的磁鏈和ΔL估計算法進行仿真分析和實驗驗證。前置永磁同步電機相關參數如表1所示。

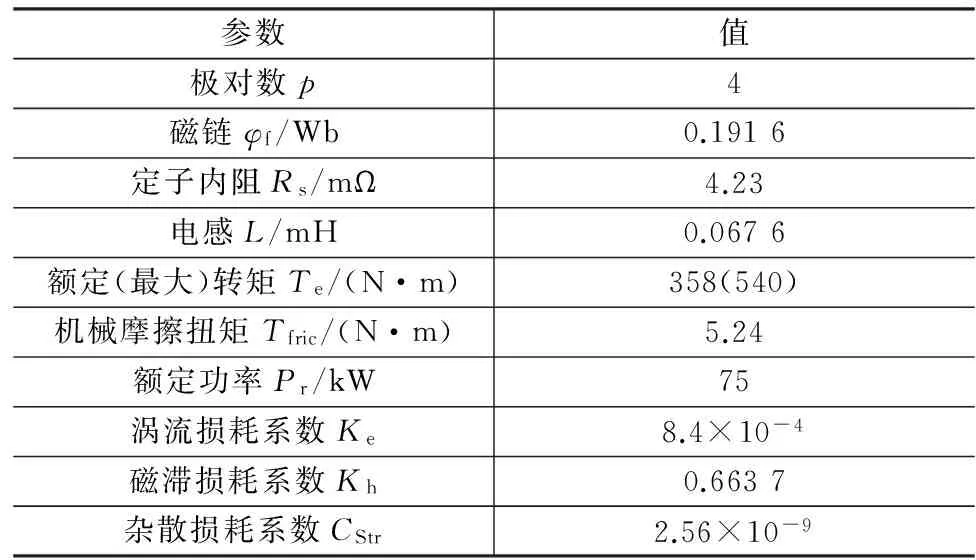
表1 內置永磁同步電機參數

3.1 仿真分析

根據圖3所示的控制框圖，在MATLAB/Simulink中建立對應的仿真模型進行仿真分析。仿真用參數設置如下： 估計器的工作頻率為2 kHz；電流環PI控制器的頻率為5 kHz；PWM 調制頻率為10 kHz；電源選用288 V的直流電壓源；忽略死區效應和電源內阻。仿真結果如圖4和圖5所示。

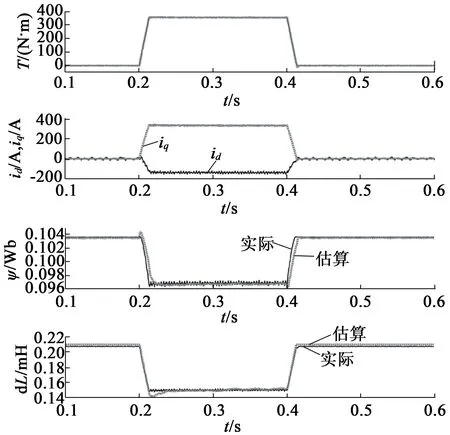
圖4 額定工況(2 000 r/min，358 N·m)下磁鏈和dL估計

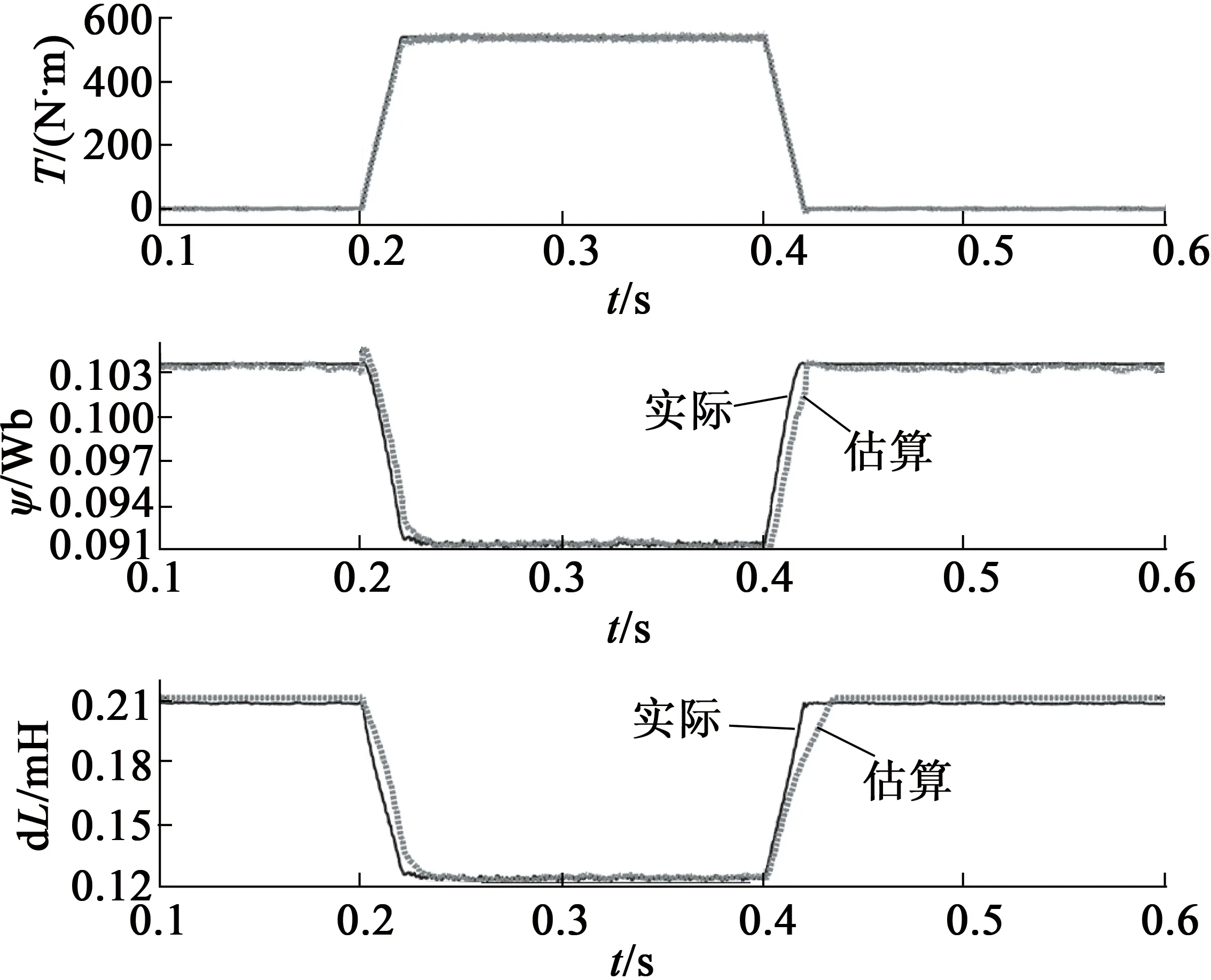
圖5 最大轉矩(1 000 r/min，540 N·m)工況下磁鏈和dL估計

由仿真結果可以看出,無論是額定工況還是最大轉矩工況，當電機運行穩定時，磁鏈估計器的輸出數值能夠較好地跟隨磁鏈參考數值；當磁鏈發生變化時，磁鏈偏差最大值在允許的范圍內。

同理，無論是額定工況還是最大轉矩工況，當電機運行穩定時，ΔL估計器的輸出數值能夠較好地跟隨ΔL參考數值；當ΔL發生變化時，ΔL偏差最大值在允許的范圍內。

另外，d軸和q軸電流實際值也可以較好地跟隨電流參考值；而且輸出轉矩同樣可以較好地跟隨目標轉矩，總體上實現了前置永磁同步電機的精確、高效控制。仿真結果表明了本文所述參數估計方法和控制策略的有效性。

3.2 實驗驗證

為進一步驗證上述參數估計方法的有效性，本文進行了相關實驗驗證。混合動力實驗臺結構如圖6所示，電源選用288 V/180 Ah的LiFePO4電池組；負載選用交流電渦流測功機；前置永磁同步電機參數與表1一致。

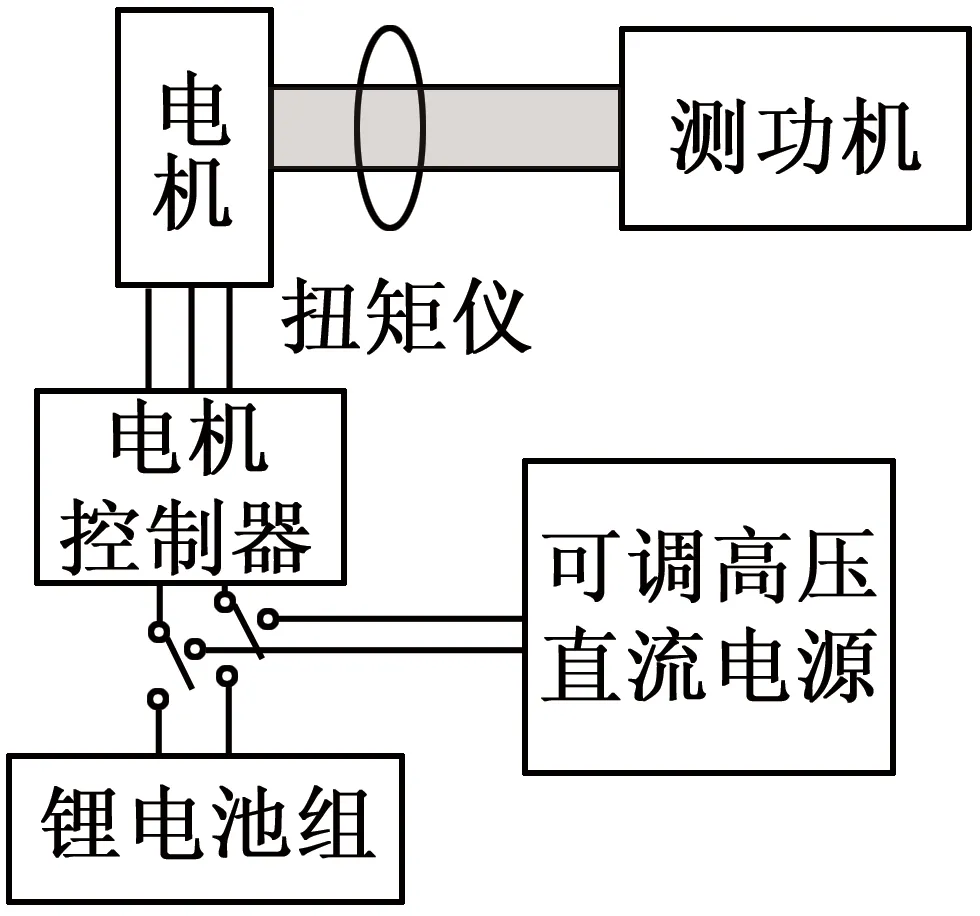
圖6 混合動力實驗臺結構

額定工況(2 000 r/min,358 N·m)和最大轉矩工況(1 000 r/min,540 N·m)下的實驗結果分別如圖7和圖8所示。與仿真結果相比，在額定工況下，實驗所得磁鏈估計數值稍大；在最大轉矩工況下，實驗所得ΔL估計數值稍大。雖然實驗條件與仿真條件存在一定的差異，但從實驗結果可以看出，實驗結果與仿真結果的趨勢完全相同。實驗結果進一步驗證了本文所述參數估計方法和控制策略可以很好地完成磁鏈和ΔL的估計，并最終實現精確的轉矩控制，表明了該方法的有效性。

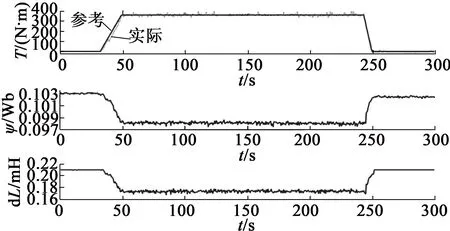
圖7 額定工況(2 000 r/min,358 N·m)下實驗結果

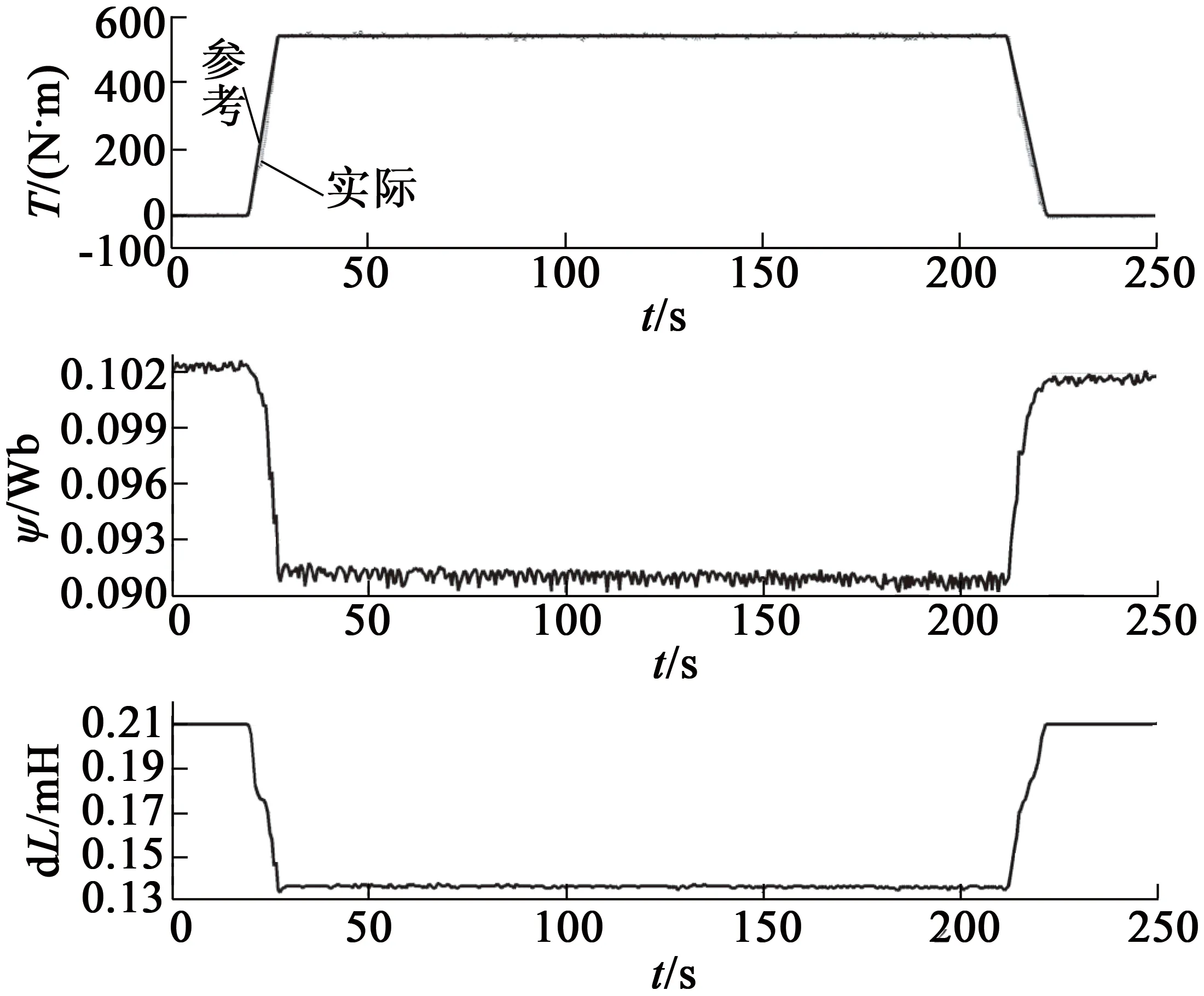
圖8 最大轉矩工況(1 000 r/min,540 N·m)下實驗結果

4 結 語

混合動力汽車作為新能源汽車的主要形式，其首選驅動電機為前置永磁同步電機。雖然前置永磁同步電機具有功率密度大、效率高等優點，但是其控制參數較多，若實現所有參數的匹配、估計和控制，需要采用信號注入法或增加傳感器數量，但是上述方法并不適用于車用永磁同步電機。本文通過分析，主要對電機磁鏈和電感進行估計。首先建立了前置永磁同步電機的數學模型；對于磁鏈估計，文中采用了前饋式電流解耦算法；對于ΔL估計，文中采用了電機功率閉環控制策略；并將參數估計和MTPA算法結合起來，實現了參數在線估計、轉矩控制等。最后通過仿真和實驗驗證了本文所述參數估計方法的可行性和有效性。所述混合動力汽車用前置永磁同步電機參數估計方法對新能源汽車的驅動系統的控制、優化具有一定的參考意義。

[1] 黃文卿,張幽彤,張興春.車用永磁同步電機功率閉環扭矩控制方法[J].北京理工大學學報,2015,35(3):246-250.

[2] 王偉光,李偉,陳衛杰.考慮磁鋼B-H特性的車用永磁同步電機MTPA控制[J].電力電子技術,2015,49(1):54-56.

[3] 廖勇,伍澤東,劉刃.車用永磁同步電機的改進MTPA控制策略研究[J].電機與控制學報,2012,16(1):12-17.

[4] 武四輩,吳志紅,朱元.車用內置式永磁同步電機電感參數辨識方法[J].農業機械學報,2013,44(8):27-32.

[5] LIU K,ZHU Z Q,STONE D A.Parameter estimation for condition monitoring of PMSM stator winding and rotor permanent magnets[J].IEEE Transactions on Industrial Electronics,2013,60(12):5902-5913.

[6] CONSOLI A,SCARCELLA G,SCELBA G,et al.Steady-state and transient operation of IPMSMs under maximum-torque-per-ampere control[J].IEEE Transactions on Industry Applications,2010,46(1):121-129.

[7] KIM S,YOON Y D,SUL S K,et al.Maximum torque per ampere (MTPA) control of IPM machine based on signal injection considering inductance saturation[J].IEEE Transactions on Power Electronics,2012,28(1):488-497.

[8] ESTIMA J O,MARQUES C A J.A new algorithm for real-time multiple open-circuit fault diagnosis in voltage-fed PWM motor drives by the reference current errors[J].IEEE Transactions on Industrial Electronics, 2013, 60(8):3496-3505.

[9] CHEN J L,LIU T H,CHEN C L.Design and implementation of a novel high-performance sensorless control system for interior permanent magnet synchronous motors[J].Electric Power Applications,IET,2010,4(4):226-240.

[10] MORIMOTO S,SANADA M,TAKEDA Y.Effects and compensation of magnetic saturation in flux-weakening controlled permanent magnet synchronous motor drives[J].IEEE Transactions on Industry Applications,1994,30(6):16-32.

[11] QI G,CHEN J T,ZHU Z Q,et al.Influence of skew and cross-coupling on flux-weakening performance of permanent-magnet brushless AC machines[J].IEEE Transactions on Magnetics,2009,45(5):2110-2117.

[12] BOILEAU T,LEBOEUF N,NAHID-MOBARAKEH B,et al.Online identification of PMSM parameters: parameter identifiability and estimator comparative study[J].IEEE Transactions on Industry Applications,2011,47(4):1944-1957.

[13] 鄭維.混合動力汽車動力總成參數匹配方法與控制策略的研究[D].哈爾濱:哈爾濱工業大學,2010.

[14] 田碩.柴油機ISG混合動力系統瞬態過程優化控制研究[D].北京：清華大學,2008.

[15] 鄧仁燕,唐娟,夏炎,等.基于前饋補償的永磁同步電機電流環解耦控制[J].電力電子技術,2013,47(6):68-70.

Research on Parameters Estimation Method of IPMSM in HEV Application

MAJian-wei,LIANGXiao-lin,ZHANGPeng-fei

(Xingtai Polytechnic College,Xingtai 054000,China)

The interior permanent magnet synchronous motor (IPMSM) is widely used in hybrid electric vehicle (HEV) with its characteristics such as wide range of constant power, large power density, and high efficiency, etc. Because of the poor working condition and big load mutation of HEV as well as the influence of temperature and magnetic saturation on IPMSM, the control performance was greatly reduced. In order to achieve the precise control of IPMSM, its mathematical model was set up in this paper. The motor torque was related with flux linkage andd,qaxis inductance difference, so the parameters estimation was mainly targeted at flux linkage and inductance. A kind of flux estimation method based on current feed-forward decoupling algorithm was put forward. It can effectively eliminate the influence of condition change on the motor. At the same time a kind ofd,qaxis inductance value estimation algorithm based on power closed loop was also put forward, which can realize the precise control of the motor. The simulation and experimental results verify the effectiveness of the parameter estimation method described in this article.

IPMSM; flux linkage estimation; hybrid electric vehicle

2016-03-04

河北省教育廳青年基金項目(QN20140202);河北省科技計劃項目(15212209);河北省教育廳項目(ZD2015015)

TM351

A

1004-7018(2016)08-0035-05

馬建偉(1981-)，男，碩士研究生，講師，研究方向為汽車電氣及控制技術。