基于廣義σ-N曲面的剩余壽命預測模型
安宗文,白學宗,高建雄
(蘭州理工大學機電工程學院,甘肅蘭州 730050)
?
基于廣義σ-N曲面的剩余壽命預測模型
安宗文,白學宗,高建雄
(蘭州理工大學機電工程學院,甘肅蘭州 730050)
為研究隨機載荷作用下結構剩余壽命的變化規律,首先從載荷作用的統計學意義出發,根據順序統計量(最大順序統計量和最小順序統計量)的性質,得到最大應力與最小應力的聯合概率分布函數;然后以廣義σ-N曲面方程為基礎,考慮載荷作用次數對疲勞壽命的影響,建立了最小應力、最大應力和剩余壽命之間的關系式,即σmin(n)-σmax(n)-Nr(n)曲面模型;最后通過具體工程實例對所建模型的有效性進行了驗證和分析。結果表明:該模型能夠有效反映最大應力和最小應力共同影響下結構剩余壽命隨載荷作用次數的變化規律,為結構的壽命預測及可靠性評估提供了理論依據。
概率分布;疲勞;剩余壽命;σ-N曲面;順序統計量;可靠性
疲勞破壞是工程結構和機械設備常見的失效形式之一。據統計,在各種機械結構的破壞中,疲勞破壞占50%~90%[1]。隨著機械設備向大型化、復雜化和高溫、高速使用環境的方向發展,由疲勞破壞而引發的斷裂失效事故更是層出不窮。因此,為防止災難性破壞事故的發生,關于疲勞破壞問題的研究引起了極大關注,其中重點為疲勞壽命預測[2-4]。
名義應力法是最早被提出并使用的抗疲勞設計方法,它以材料或結構的σ-N曲線為基礎,根據結構危險部位的應力集中系數及名義應力,運用累積損傷理論,對結構的疲勞壽命進行預測[5]。迄今為止,名義應力法仍然是工程界最廣泛采用的抗疲勞設計方法[6]。
由于疲勞問題的復雜性,考慮多種因素的綜合影響,要對結構的疲勞壽命做出較為精確的預測,就需要選擇合適的壽命預測模型[7-9]。事實上,結構在隨機載荷的作用過程中,其所承受的應力幅值和應力均值都是隨機變化的。同時,大量工程實踐表明:結構的疲勞壽命和疲勞損傷是由應力幅值和應力均值2個隨機變量共同控制的,而傳統的名義應力法只考慮了應力幅值的隨機變化對疲勞壽命造成的影響,其預測結果難免有失偏頗[10-11]。
許多學者對應力幅值和應力均值共同影響下結構的疲勞壽命預測問題進行了研究。張書明等[12]考慮應力幅值和應力均值的共同作用,構建了沃克爾(Walker)型裂紋擴展壽命的σa-σm-N*廣義斷裂性能曲面,并討論了該廣義斷裂性能曲面的測定與擬合方法;閻楚良等[13]利用σ-N曲線方程和等壽命曲線,建立了應力幅值、應力均值和疲勞壽命的關系式(即廣義σ-N曲面方程),并以此作為疲勞壽命估算和疲勞可靠性設計的依據;廖強等[14]基于Goodman型等壽命曲線和Gerber型等壽命曲線,分別建立了相應的廣義σ-N曲面方程,并結合Miner累積損傷理論對渦輪盤的疲勞壽命進行了預測。熊峻江等[15]考慮應力幅值和應力均值對疲勞壽命的影響,提出了廣義疲勞等壽命曲線P-σa-σm,并以此為基礎推導出了二維疲勞極限的概率分布。倪侃等[16]基于損傷力學理論,建立了等幅加載下個體的D-σa-σm-N等損傷曲面,推導出二維個體Miner準則,并用測度論給出了證明。
為研究隨機載荷多次作用時結構剩余壽命的變化規律,本文以廣義σ-N曲面為基礎,從載荷作用的統計學意義出發,根據順序統計量的性質,建立了最小應力、最大應力和剩余壽命之間的關系式(即σmin(n)-σmax(n)-Nr(n)曲面方程模型)。該模型為隨機載荷多次作用下結構的剩余壽命預測及可靠性評估提供了理論依據。
1 廣義σ -N曲面方程
1.1 σ -N曲線和等壽命曲線
對于材料的疲勞問題,最基本同時也是很有效的研究是σ-N曲線[17],它描述的是循環應力σ(σa或σmax)與失效循環數(疲勞壽命)N之間的對應關系。
σ -N曲線作為結構疲勞壽命預測的基礎,是用一組標準試樣(一般為7~10個),在給定的應力比r下,施加不同的循環應力σ進行疲勞試驗,記錄相應的疲勞壽命N,通過擬合(σ,N)數據便可得到材料的σ -N曲線。描述材料σ -N曲線最常用形式是如式(1)所示的冪函數式[18]。
(1)
式中:m和C是與材料應力比、加載方式等有關的參數。

圖1 等壽命曲線Fig.1 Constant life curve
反映材料疲勞性能的基本σ-N曲線是在應力比r=-1(即平均應力為零)的對稱循環加載條件下獲得的。事實上,大多數工程結構在實際運行過程中所承受的應力均值并不為零,若要考慮平均應力(或應力比)的變化對材料疲勞性能的影響,就需要用到等壽命曲線。
人們通過對大量疲勞試驗數據的統計分析,提出了多種經驗性等壽命曲線方程,如Goodman直線方程、Gerber拋物線方程和Soderberg直線方程等,如圖1所示。
圖中:橫坐標軸σm為平均應力,縱坐標軸σa為應力幅值,σs為材料的屈服強度,σb為材料的斷裂靜強度,σ-1為對稱循環下材料的強度極限。
由圖1可知,Soderberg直線模型過于保守,Gerber拋物線模型偏于危險,而Goodman直線模型相對比較合適。Goodman直線模型的函數表達式如式(2)所示。
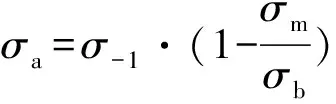
(2)
式中:σb為材料的斷裂靜強度;σ-1為材料的對稱循環下材料的強度極限。
根據式(2)所示的Goodman直線模型,在已知材料的強度極限σb和基本σ-N曲線時,便可對材料在不同平均應力(或應力比)下的疲勞性能進行評估。
1.2 廣義σ-N曲面
結構在服役過程中常受隨機循環載荷的作用,其疲勞壽命與應力幅值和平均應力有關。描述材料疲勞性能的廣義σ -N曲面,能夠很好地反映應力幅值和應力均值共同影響下結構的疲勞壽命問題,其構建過程如下:
在應力幅值σa和應力比r已知的情況下,最大應力σmax和平均應力σm可分別表示為

(3)
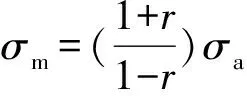
(4)
將式(3)代入式(1),可得:

(5)
對式(5)進行變換,可得:
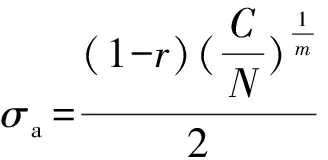
(6)
將式(6)代入式(4),可得:
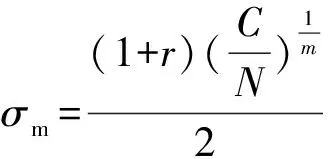
(7)
將式(6)和式(7)代入式(2),可得:
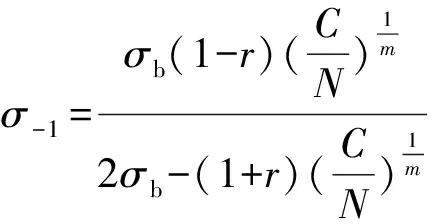
(8)
將式(8)代入式(2),可得:

(9)
對式(9)進行變換,可得:
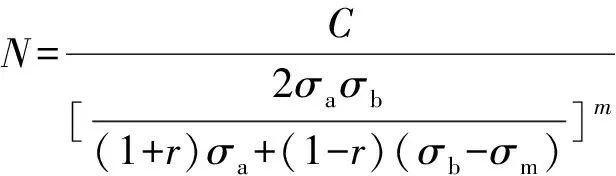
(10)
式(10)即為描述材料疲勞性能的廣義σ-N曲面方程。
2 σmin(n)-σmax(n)-Nr(n)曲面模型
2.1 順序統計量
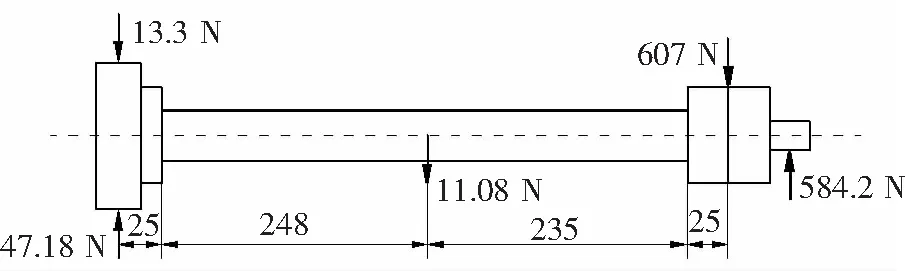
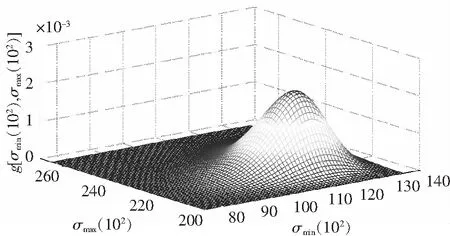
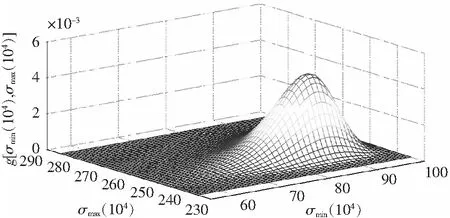
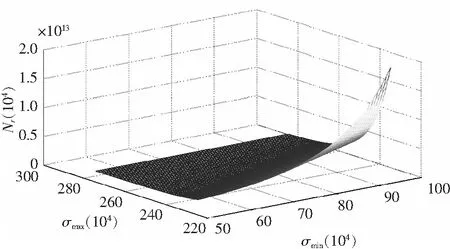
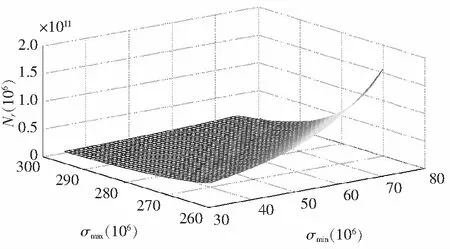
順序統計量(或稱次序統計量)是數理統計學中廣泛應用的一類統計量。設X1,X2,…,Xn是來自同一隨機變量母體的一組樣本觀測值,母體的累積分布函數為F(x),概率密度函數為f(x)。將樣本觀測值按從小到大遞增順序排列,即X(1) (11) 其中X(1)=min(X1,X2,…,Xn)和X(n)=max(X1,X2,…,Xn)分別稱為最小順序統計量和最大順序統計量,其對應的概率密度函數分別為 g1(x)=n[1-F(x)]n-1f(x) , (12) gn(x)=n[F(x)]n-1f(x) , (13) 任意2個順序統計量X(k)和X(j)的聯合概率密度函數g(xk,xj)為 (14) 特別的,當k=1,j=n時,最大順序統計量與最小順序統計量的聯合概率密度函數為 n(n-1)[F(xn)-F(x1)]n-2f(x1)f(xn)。 (15) 2.2 σmin(n)-σmax(n)-Nr(n)曲面方程 文獻[13]中提到,當載荷譜為雨流計數法獲得的σa和σm聯合分布時,可直接利用式(10)所示的廣義σ-N曲面方程,進行疲勞壽命估算或疲勞可靠性設計。然而,由于受到技術及經濟條件的限制,在實際工程中,利用雨流計數法只能獲得關于應力幅值σa和平均應力σm有限的試驗數據,基于這些數據一般也只能獲得σa和σm的邊緣分布函數。根據概率論的知識可知,除了變量的聯合分布函數是多維正態分布外,根據隨機變量的邊緣分布不能唯一確定隨機變量的聯合概率分布函數。因此,由于不能精確確定σa和σm的聯合分布,式(10)在實際的工程應用中受到很大限制。其實,最小應力σmin和最大應力σmax的聯合分布可以根據最小順序統計量和最大順序統計量的聯合分布來確定,如式(15)所示,該式能夠反映聯合分布隨載荷作用次數的變化規律。為此,本文首先將應力幅值σa和平均應力σm對疲勞壽命的影響等價地轉化為最小應力σmin和最大應力σmax對疲勞壽命的影響。然后根據順序統計量的性質得到最小應力σmin與最大應力σmax的聯合分布函數。最后得到描述材料疲勞性能的廣義σmin(n)-σmax(n)-Nr(n)曲面方程。具體過程如下。 在最大應力σmax和最小應力σmin已知的情況下,應力幅值σa和平均應力σm可分別表示為 (16) (17) 將式(16)和式(17)代入式(10),可得: (18) 根據順序統計量的性質,最大應力σmax(對應最大順序統計量)與最小應力σmin(對應最小順序統計量)隨載荷作用次數n的變化而變化。因此,疲勞壽命N也隨載荷作用次數的變化而變化。故式(18)實際上是一個動態模型,可改寫為 (19) 式中σmax(n),σmin(n)和Nr(n)分別表示載荷作用n次時的最大應力、最小應力和剩余壽命。 設應力的概率密度函數為fσ(σ),累積分布函數為Fσ(σ)。若記x1=σmin(n)=σ1,xn=σmax(n)=σn,根據式(12)和式(13),可分別得到最小應力σmin(n)和最大應力σmax(n)的概率密度函數: g1(σ1)=n[1-Fσ(σ1)]n-1fσ(σ1), (20) gn(σn)=n[Fσ(σ1)]n-1fσ(σn), (21) 根據式(15),可得最大應力與最小應力的聯合概率密度函數: g[σ1,σn]=n(n-1)[Fσ(σn)-Fσ(σ1)]n-2fσ(σ1)fσ(σn)。 (22) 由式(22)可知,最小應力和最大應力的聯合概率密度函數隨載荷作用次數n的變化而變化,該式能夠反映載荷特征隨作用次數的變化規律。 圖2 轉子軸結構圖Fig.2 Structure diagram of rotor shaft 某轉動軸,材料為熱軋16Mn合金鋼,全功率運轉時的受力如圖2所示,經實測作用于軸的載荷F1=(607.4±30)N,扭矩MT=(133±27)N·m,安裝誤差產生的載荷F2=13.3 N,軸質量F3=11.08 N。軸的設計參數為直徑d=(16±0.21)mm,軸肩處的圓角半徑R=3.2 mm[20]。 3.1 軸在危險截面處的應力分布參數 根據圖2,由力學模型計算得到危險截面上彎矩的均值和標準差分別為μMn=14.1N·m,σMn=0.189N·m。 危險截面上扭矩的均值和標準差分別為 進一步,可得到應力的均值和標準差分別為 應力的概率密度函數可表示為 3.2 計算應力水平與疲勞壽命之間的關系 在熱軋16Mn合金鋼的疲勞壽命試驗中,選取了σ1=394 MPa,σ2=373 MPa和σ3=344 MPa應力水平。在這3個恒幅循環載荷作用下的疲勞壽命試驗結果如表1所示[19]。 通過對試驗數據的擬合,可得材料疲勞壽命與應力水平之間的關系為通過對試驗數據的擬合,得 表1 疲勞壽命試驗結果 材料疲勞壽命與應力水平之間的關系為σ13.221 9N=2.279 6×1039,熱軋16Mn合金鋼強度極限σb=586 MPa[21]。 3.3 預測軸的疲勞壽命 根據式(20)和式(21),可得載荷作用次數分別為n=102,104,106時最大應力σmax(n)與最小應力σmin(n)的概率密度函數,如圖3所示。 圖3 順序統計量Fig.3 Order statistics 根據式(22),可得載荷作用次數分別為n=102,104,106時最大應力σmax(n)與最小應力σmin(n)的聯合概率密度函數,分別如圖4-圖6所示。根據式(19),可得載荷作用次數分別為n=102,104,106時轉子軸的剩余壽命曲面,如圖7-圖9所示。 圖4 n=102時σmax(n)與σmin(n)聯合概率密度函數Fig.4 Joint probability density function of σmax(n) and σmin(n) when n=102 圖5 n=104時σmax(n)與σmin(n)聯合概率密度函數Fig.5 Joint probability density function of σmax(n) and σmin(n) when n=104 圖6 n=106時σmax(n)與σmin(n)聯合概率密度函數Fig.6 Joint probability density function of σmax(n) and σmin (n) when n=106 圖7 n=102時剩余壽命曲面Fig.7 Residual life surface when n=102 圖8 n=104時剩余壽命曲面Fig.8 Residual life surface when n=104 圖9 n=106時剩余壽命曲面Fig.9 Residual life surface when n=106 由圖7-圖9可知,轉子軸的剩余壽命Nr(n)受最小應力σmin(n)和最大應力σmax(n)的共同影響,并且隨載荷作用次數n的變化而變化。在不同的載荷作用次數n下,由于最小應力σmin(n)和最大應力σmax(n)的聯合概率密度函數發生了變化,因此導致轉子軸具有不同的剩余壽命,而且隨著載荷作用次數n的增加,轉子軸的剩余壽命逐漸降低。 1) 考慮應力幅值和應力均值對疲勞壽命的影響,構建了能反映結構疲勞性能的廣義σ-N曲面模型。 2) 以廣義σ-N曲面為基礎,根據順序統計量的性質,建立了最小應力、最大應力和剩余疲勞壽命的關系式,即σmin(n)-σmax(n)-Nr(n)曲面方程模型,并通過實例分析對所建模型的有效性進行了驗證和分析。 [1] 溫熙森, 陳循, 張春華, 等. 可靠性強化試驗理論與應用[M]. 北京: 科學出版社, 2007. [2] 袁熙, 李舜酩. 疲勞壽命預測方法的研究現狀與發展[J]. 航空制造技術, 2005(12): 80-84. YUAN Xi, LI Shunming. Research status and development of forecast method of fatigue life[J]. Aeronautical Manufacturing Technology, 2005(12): 80-84. [3] 黃寧. 大型結構件的疲勞壽命預測方法研究[D]. 長沙: 中南大學, 2012. HUANG Ning. Research on Fatigue Life Prediction Methods for Large-Scale Components[D]. Changsha: Central South University, 2012. [4] 雷冬. 疲勞壽命預測若干方法的研究[D]. 合肥: 中國科學技術大學, 2006. LEI Dong. Research for Several Methods of Fatigue Life Prediction[D]. Hefei: University of Science and Technology of China, 2006. [5] 姚衛星. 結構疲勞壽命分析[M]. 北京: 國防工業出版社, 2003. [6] 武瀅, 謝里陽. 隨機載荷作用下疲勞壽命分布預測模型[J]. 工程設計學報,2010,17(6):435-438. WU Ying, XIE Liyang. Prediction on probability distribution of fatigue life under spectrum loading[J]. Journal of Engineering Design,2010,17(6):435-438. [7] VERREMAN Y, LIMODIN N. Fatigue notch factor and short crack propagation[J]. Engineering Fracture Mechanics, 2008, 75(6): 1320-1335. [8] 董月香, 高增梁. 疲勞壽命預測方法綜述[J]. 大型鑄鍛件, 2006(3):38-40.DONG Yuexiang, GAO Zengliang. General description of the fatigue life prediction method[J]. Heavy Casting and Forging, 2006(3):38-40. [9] 鄔華芝, 高德平, 郭海丁. 概率疲勞破壞壽命特性研究綜述[J]. 湖北工學院學報, 2002, 17(3): 18-22. WU Huazhi, GAO Deping, GUO Haiding. The review of probability fatigue damage life characteristics research[J]. Journal of Hubei University of Technology, 2002, 17(3): 18-22. [10]WU Ying, XIE Liyang, ZHANG Xiaojin. Study on fatigue life prediction under spectrum loading[J]. Journal of Materials and Metallurgy, 2011, 10(2): 150-153. [11]ZHAO Lihui, ZHENG Songlin, FENG Jinzhi. Fatigue life prediction under service load considering strengthening effect of loads below fatigue limit[J]. Chinese Journal of Mechanical Engineering, 2014, 6(3): 3-4. [12]張書明, 閻楚良, 高鎮同. 廣義斷裂性能曲面[J]. 機械工程學報, 2001, 37(12): 37-42. ZHANG Shuming, YAN Chuliang, GAO Zhentong. Generalized surface of fracture behavior[J]. Chinese Journal of Mechanical Engineering, 2001, 37(12): 37-42. [13]閻楚良, 高鎮同. 疲勞性能廣義σ-N曲面[J]. 機械工程學報, 1999, 1: 103-106. YAN Chuliang, GAO Zhentong. Generalizedσ-Ncurved surface of fatigue character[J]. Chinese Journal of Mechanical Engineering, 1999, 1: 103-106. [14]廖強, 黃洪鐘, 朱順鵬, 等. 基于廣義σ-N曲面的渦輪盤疲勞壽命預測[J]. 電子科技大學學報, 2013, 42(2): 316-320. LIAO Qiang, HUANG Hongzhong, ZHU Shunpeng, et al. Turbine disk fatigue life prediction based on generalizedσ-Nsurface[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(2): 316-320. [15]熊峻江, 武哲, 高鎮同. 廣義疲勞等壽命曲線與二維疲勞極限概率分布[J]. 應用數學和力學, 2002, 23(10): 1055-1060. XIONG Junjiang, WU Zhe, GAO Zhentong. Generalized fatigue constant life curve and two dimensional probabilistic distribution of fatigue limit[J]. Applied Mathematics and Mechanics, 2002, 23(10): 1055-1060. [16]倪侃, 高鎮同. 疲勞可靠性二維概率Miner準則[J]. 固體力學學報, 1996, 17(4): 365-371. NI Kan, GAO Zhentong. Two-dimensional probabilistic Miner’s rule in fatigue reliability[J]. Chinese Journal of Solid Mechanics, 1996, 17(4): 365-371. [17]YAO J T P, KNZIO F, WEN Y, et al. Stochastic fatigue, fracture and damage analysis[J]. Structural Safety, 1986, 3(3/4): 231-267. [18]SIJVE J. Fatigue of Structures and Materials[M]. Berlin: Springer, 2009. [19]謝里陽, 王正, 周金宇, 等. 機械可靠性基本理論與方法[M]. 北京: 科學出版社, 2009. [20]王正, 王增全, 何洪. 隨機載荷循環作用下的機械結構疲勞壽命預測模型[J]. 中國機械工程, 2012, 23(1): 98-101. WANG Zheng, WANG Zengquan, HE Hong. Predicting model for fatigue life of mechanical structures under random cyclic loads[J]. China Mechanical Engineering, 2012, 23(1): 98-101. [21]《機械工程材料性能數據手冊》編委會.機械工程材料性能數據手冊[M]. 北京: 機械工業出版社, 1995. A residual life prediction model based on the generalizedσ-Ncurved surface AN Zongwen, BAI Xuezong, GAO Jianxiong (School of Mechatroni Engineering, Lanzhou University of Technology, Lanzhou, Gansu 730050, China) In order to investigate change rule of the residual life of structure under random repeated load, firstly, starting from the statistic meaning of random repeated load, the joint probability density function of maximum stress and minimum stress is derived based on the characteristics of order statistic (maximum order statistic and minimum order statistic); then, based on the equation of generalizedσ-Ncurved surface, considering the influence of load cycles number on fatigue life, a relationship among minimum stress, maximum stress and residual life, that is theσmin(n)-σmax(n)-Nr(n) curved surface model, is established; finally, the validity of the proposed model is demonstrated by a practical case. The result shows that the proposed model can reflect the influence of maximum stress and minimum stress on residual life of structure under random repeated load, which can provide a theoretical basis for life prediction and reliability assessment of structure. probability distribution; fatigue; residual life;σ-Ncurved surface; order statistic; reliability 1008-1542(2016)03-0213-07 10.7535/hbkd.2016yx03001 2015-12-09; 2015-12-31;責任編輯:張 軍 國家自然科學基金(51265025) 安宗文(1968—),男,甘肅景泰人,教授,博士生導師,主要從事機械結構可靠性設計理論及相關系統可靠性建模方面的研究。 E-mail:anzongwen@163.com TB A 安宗文,白學宗,高建雄.基于廣義σ -N曲面的剩余壽命預測模型[J].河北科技大學學報,2016,37(3):213-219. ANZongwen,BAIXuezong,GAOJianxiong.Aresiduallifepredictionmodelbasedonthegeneralizedσ -Ncurvedsurface[J].JournalofHebeiUniversityofScienceandTechnology,2016,37(3):213-219.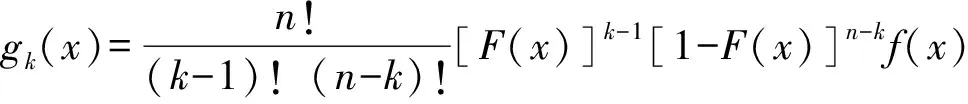
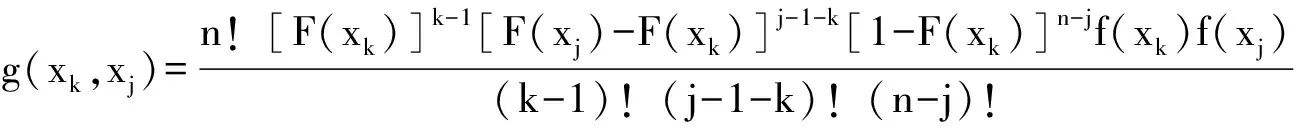

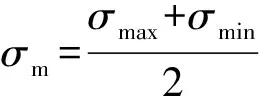
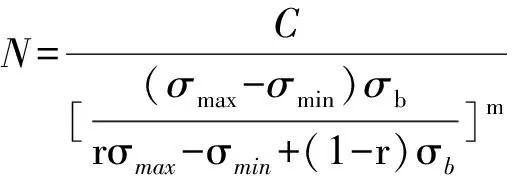

3 實例分析
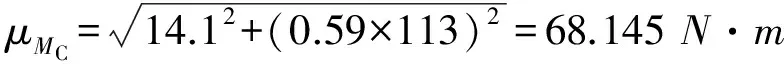



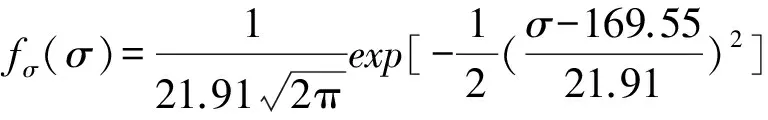




4 結 論

