結構健康監測系統的數據異常識別

范時梟+張金輝+張其林

摘要： 結合機器學習方法對結構健康監測系統采集的原始數據進行初步的自動化分析，以達到降低進一步分析的計算量、提高分析子系統精度的目的.以上海中心和蘭州西站監測系統為背景，利用機器學習方法研究數據異常識別問題，優化數據分析預警子系統.使用單變量特征選擇提取利于識別的特征向量， 對比分析在結構健康監測中各類支持向量機（Support Vector Machine，SVM）的優劣，組合利用不同SVM的優勢減少異常數據的漏報和誤報.該方法已被應用于上海中心和蘭州西站的結構健康監測系統中.

關鍵詞： 結構健康監測； 數據識別； 單變量特征選擇； 支持向量機； 主成分分析； 機器學習； 數據降維

中圖分類號： TU312.3 文獻標志碼： B

0 引 言

自20世紀70年代以來，結構健康監測逐步進入土木工程領域，使結構維護、預警、狀態評估具有較可靠的指導.隨著計算機和網絡技術的飛速發展，監測系統也應運而生.[1-2]在結構損傷識別和預警問題上，國內外學者先后將神經網絡算法[3-4]、模糊理論[5]、小波分析[6]和遺傳算法[7]等運用于分析預警子系統中.但是，大型建筑結構健康監測產生的數據量巨大，以上海中心為例，應布置400多個測量點位，其中頻率100 Hz的動態點位超過150個，每天產生數十GB數據量，若直接將數據應用于結構模態識別計算分析，進行損傷識別，其計算量十分驚人.現階段，普遍采用方法的是利用定值的信號閾值進行數據篩選，結合人工定時選取某段時間數據進行計算分析，因此效率較低且易漏報和誤報異常數據.進行初步的數據異常識別有助于縮小分析范圍、降低計算負荷.曾有學者針對橋梁結構提出數據異常診斷方法，但經過上海中心監測數據測試發現此方法對于建筑結構效果不佳.本文旨在對監測數據進行第一層的異常識別，提供對內的預警，降低分析子系統的計算壓力.

1 特征向量降維方法

監測數據的統計特征眾多，采用一定的數據降維方法處理后可得到正常數據與異常數據之間差別更明顯的統計特征，即對異常識別來說更有效的特征值，便于數據分類.同時，特征向量維度降低，進一步分析時計算量將顯著降低.本文對比主成分分析（Principal Component Analysis，PCA）法[8]與單變量特征選擇（Univariate Feature Selection，UFS）法[9]2種方法，結合實際數據分析其在結構健康監測中進行特征向量降維的優劣.

1.1 主成分分析法

PCA法將數據矩陣

[WTHX]X[WTBX]的行視為來自p個隨機變量x的觀測值，降低

[WTHX]X[WTBX]的維度主要通過線性組合實現，將n維特征向量映射到k維上（k

1.2 單變量特征選擇法

UFS法能夠對每一個特征進行測試，衡量該特征與響應變量之間的關系，根據得分去掉可分性不好的特征.分類問題可采用方差分析對特征進行打分.

方差分析用于2個及2個以上樣本均數差別的顯著性檢驗，其將總的試驗數據的波動分為反映因素水平改變引起的波動和反映隨機因素引起的波動，然后進行比較判斷.

2 數據識別方法

利用統計學習的分類方法，依據監測數據特征值向量對每段監測數據進行分類，可達到識別異常數據的目的.[10]

2.1 支持向量機原理

支持向量機（Support Vector Machine，SVM）[11]是一種二分類模型，其基本模型是定義在特征空間上的間隔最大線性分類器.SVM的目標便是尋找所有可將2類數據分離的超平面中基于支持向量幾何間隔最大的一個，為約束最優化的問題.實際數據常常不會是完全線性可分的，若去掉少量點后能變為線性可分的數據集即線性近似可分，可使用松弛變量，并引入懲罰參數C>0，使原問題的間隔最大化變為軟間隔最大化.對于完全線性不可分數據，引入核技巧可使其成為實質上的非線性分類器.

2.2 非線性分類SVM

動態監測數據的數據種類繁多，且在建筑施工或使用過程中獲得的監測數據受各種外部因素的干擾，常產生非線性分類問題，即不存在一個超平面可將2類數據分離或近似分離，需使用非線性分類器進行分類.對于此類問題，核心的求解思路為利用非線性變換使原空間的2類點映射到新空間，使問題在新空間中變為線性分類問題，常采用核技巧來實現.

2.3 一類SVM

一類SVM[12]與前文中所述普通二分類SVM的不同之處在于其只有一類數據，2類數據間的幾何間隔便不存在了.一類SVM的基本思路是將數據映射到高維特征空間，使其具有更好的聚集性，在特征空間中找到一個使數據與坐標原點幾何間隔最大的超平面.

3 工程應用

3.1 數據采集與預處理

本文中使用的數據分別為由上海中心結構健康監測系統采集的臺風前后建筑頂端處風速數據以及由蘭州西站結構健康監測系統采集的地震前后網架某處加速度數據.2套系統均采用B/S結構建設，使

用Node.js結合Mongodb數據庫編寫，以達到實時、快速存取大量數據，便捷查看、調用數據的目的.為達到分析處理每日海量的監測數據和實時分析數據、查看結果的目的，本文數據分析程序主體使用Node.js編寫.2015年13號臺風蘇迪羅過境前后上海中心風速時程圖見圖1， 2015年4月15日甘肅省地震前后蘭州西站加速度時程圖見圖2.

觀察圖1中的風速時程圖，雖然臺風過境時風速數據整體數值比臺風過境后更大，但由于風速數據波動較大，所以2類數據有大量交叉點.此種情況下簡單利用閾值進行數據識別則效果比較差.為定量展示本文數據識別方法在真實環境中復雜情況下的識別效果，將風速數據以臺風過境時的圖1a和

1b的所有數據作為異常數據，以過境后圖1c和1d的所有數據作為正常數據，測試本文的識別方法對于2類數據的識別準確率.

同樣，加速度數據以地震作用時正段數據作為異常類數據，即圖2中500～640 s及2 480～2 540 s這2段數據，剩余所有數據作為正常數據.

對采集的數據首先進行小波閾值降噪，閾值計算采用斯坦無偏風險計算方法.信號采集頻率為100 Hz，以10 s信號為一個樣本，每小時360個樣本，每個樣本包含1 000個信號數據，2種分類器的學習集和測試集樣本量

每個樣本提取均值、最大值、最小值、峰值、整流均值、標準差、偏度、峰度、均方根、波形指標、峰值指標、脈沖指標、頻率中心、均方根頻率和頻率標準差共15個特征值組成特征向量.特別指出，均值主要用于描述信號的穩定分量，均方根值主要用于描述振動信號的能量，峰值指標、脈沖指標主要用于檢測信號中的沖擊.[13]

3.2 2種降維方法對比分析

3.2.1 PCA法降維

上海中心風速數據前3個主成分組成的特征向量空間分布見圖3a，3個主成分累計貢獻率為88%；蘭州西站加速度數據前3個主成分組成的特征向量空間分布見圖3b，3個主成分累計貢獻率為81%；圖中灰色點為異常數據，黑色點為正常數據.

從圖3來看，對于這2種監測數據，使用PCA

法處理數據后未能保持較好的可分性.初步分析是由于PCA法的核心是尋找特征空間中最大方差的線性組合以達到降低向量維度的目的，這是基于最大方差理論認為此方向保留的信息最多，然而當實際不同類別的區別信息保留于最小方差方向時，其并未將數據分類考慮在內.

3.2.2 UFS法降維

上海中心風速數據得分前三名的特征值組成特征向量的空間分布見圖4a；蘭州西站加速度數據得分前三名的特征值組成特征向量的空間分布見圖4b；圖中灰色點為異常數據，黑色點為正常數據.

從圖4來看，使用UFS方法選擇出的特征向量具有很好的可分性.對比不同特征值得分，在保證數據可分的同時盡量保留較多的信息，最終選擇得分前八名的特征值.風速數據取均值、均方根、最小值、峰值指標、脈沖指標、最大值、波形指標、偏度，加速度數據取均方根頻率、頻率中心、整流均值、標準差、均方根、最大值、峰值和最小值.

3.3 2種SVM的異常識別效果分析

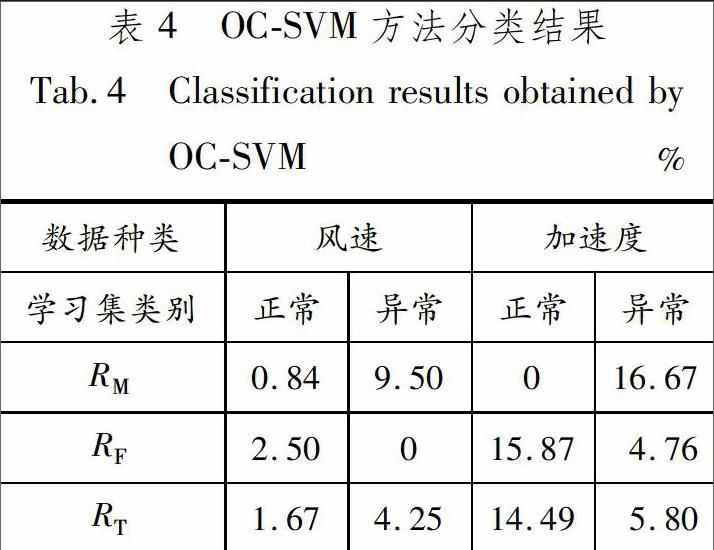
從數據中可以看出，普通二分類SVM的整體分

類錯誤率較低，錯誤集中在漏報上.一類SVM的整體錯誤率較高，其中以正常樣本為學習集時易出現誤報，以異常樣本為學習集時易出現漏報.當以正常集為學習集時，一類SVM比普通二分類SVM誤報率更高、漏報率更低.

3.4 基于支持向量的異常識別方法改進

在建筑結構健康監測中，誤報導致檢修成本提高、干擾正常使用等問題，漏報可能會導致建筑物舒適性差、甚至危及人身或財產安全.將2種方法結合：第一步，學習集采用正常數據，預設類別為正常，對測試數據進行一類SVM分類；第二步，分類結果為異常的再用普通二分類SVM進行分類.分類結果見表5.對比前2種方法單獨使用，結果顯示其錯誤率下降，漏報率與誤報率均為最優結果.

4 結 論

本文采用機器學習方法，提出對建筑結構健康監測數據進行初步識別的新方法，并將其在上海中心和蘭州西站的B/S監測數據系統中編程實現.

在數據特征向量的提取與選擇上，分析常用PCA法在監測數據特征提取中使不同數據混合不利于分類的問題，并與UFS法對比后，選擇利于識別異常數據的特征向量.

在使用SVM進行數據分類時，分析2種SVM分類方法運用在監測數據分類中的效果，結合運用2種SVM進行數據處理的有效方法，組合利用二者的優勢使異常識別的漏報和誤報減少.

采用這種數據初步識別辦法，降低分析子系統運算壓力，并且減少分析系統遺漏地震、臺風、儀器故障及其他問題導致的數據異常的可能，對優化改進結構預警系統有一定意義.

參考文獻：

[1]

李慧， 周文松， 歐進萍， 等. 大型橋梁結構智能健康監測系統集成技術研究[J]. 土木工程學報， 2006， 39（2）： 46-52. DOI： 10.3321/j.issn：1000-131X.2006.02.010.

LI H， ZHOU W S， OU J P， et al. A study on system integration technique of intelligent monitoring systems for soundness of long-span bridges[J]. China Civil Engineering Journal， 2006， 39（2）： 46-52. DOI： 10.3321/j.issn：1000-131X.2006.02.010.

[2] 李惠， 鮑躍全， 李順龍， 等. 結構健康監測數據科學與工程[J]. 工程力學， 2015， 32（8）： 1-7. DOI： 10.6052/j.issn.1000-4750.2014.08.ST11.

LI H， BAO Y Q， LI S L， et al. Data science and engineering for structural health monitoring[J]. Engineering Mechanics， 2015， 32（8）： 1-7. DOI： 10.6052/j.issn.1000-4750.2014.08.ST11.

[3] AVCI E， SENGUR A， HANBAY D. An optimum feature extraction method for texture classification[J]. Expert Systems with Applications， 2009， 36（3）： 6036-6043. DOI： 10.1016/j.eswa.2008.06.076.

[4] AVCI E， TURKOGLU I. An intelligent diagnosis system based on principle component analysis and ANFIS for the heart valve diseases[J]. Expert Systems with Applications， 2009， 36（2）： 2873-2878. DOI： 10.1016/j.eswa.2008.01.030.

[5] 李瀟， 楊國安， 吳貞煥， 等. 基于聲發射信號模糊函數綜合相關系數的海洋平臺各類損傷識別方法[J]. 機械工程學報， 2014， 50（22）： 1-9. DOI： 10.3901/JME.2014.22.001.

LI X， YANG G A， WU Z H， et al. Damage identification method of offshore platforms by ambiguity function integrated correlation coefficient of the acoustic emission signals[J]. Journal of Mechanical Engineering， 2014， 50（22）： 1-9. DOI： 10.3901/JME.2014.22.001.

[6] 鐘儒勉， 宗周紅， 鄭沛娟， 等. 基于節點曲率和小波分析的梁式橋多尺度損傷識別[J]. 振動與沖擊， 2015， 34（12）： 108-114. DOI： 10.13465/j.cnki.jvs.2015.12.019.

ZHONG R M， ZONG Z H， ZHEN P J， et al. Damage identification method of girder bridge based on nodal curvatures and wavelet analysis[J]. Journal of Vibration and Shock， 2015， 34（12）： 108-114. DOI： 10.13465/j.cnki.jvs.2015.12.019.

[7] 傅大寶， 葉肖偉， 倪一清， 等. 基于遺傳算法和有限混合分布的應力譜多模態建模[J]. 工程力學， 2014， 31（5）： 172-179. DOI： 10.6052/j.issn.1000-4750.2012.12.0949.

FU D B， YE X W， NI Y Q， et al. Multi-modal modelling of stress spectrum using genetic algorithm and finite mixture distributions[J]. Engineering Mechanics， 2014， 31（5）： 172-179. DOI： 10.6052/j.issn.1000-4750.2012.12.0949.

[8] 朱軍華， 余嶺. 基于頻響函數的結構健康監測主成分分析法[J]. 振動與沖擊， 2011， 30（5）： 111-115. DOI： 10.3969/j.issn.1000-3835.2011.05.023.

ZHU J H， YU L. A PCA-based algorithm for structural health monitoring using frequency response functions[J]. Journal of Vibration and Shock， 2011， 30（5）： 111-115. DOI： 10.3969/j.issn.1000-3835.2011.05.023.

[9] DROTR P， GAZDA J， SMKAL Z. An experimental comparison of feature selection methods on two-class biomedical datasets[J]. Computers in Biology and Medicine， 2015， 66： 1-10. DOI： 10.1016/j.compbiomed.2015.08.010.

[10] 袁慎芳， 梁棟， 高寧， 等. 基于結構健康監測系統的橋梁數據異常診斷研究[J]. 電子科技大學學報， 2013， 42 （1）： 69-74. DOI： 10.3969/j.issn.1001-0548.2013.01.016.

YUAN S F， LIANG D， GAO N， et al. The bridge data diagnosis research based on structural health monitoring system[J]. Journal of University of Electronic Science and Technology of China， 2013， 42（1）： 69-74. DOI： 10.3969/j.issn.1001-0548.2013.01.016.

[11] 丁世飛， 齊丙娟， 譚紅艷. SVM理論與算法研究綜述[J]. 電子科技大學學報， 2011， 40（1）： 1-10. DOI： 10.3969/j.issn.1001-0548.2011.01.001.

DING S F， QI B J， TAN H Y. An overview on theory and algorithm of support vector machines[J]. Journal of University of Electronic Science and Technology of China， 2011， 40（1）： 1-10. DOI： 10.3969/j.issn.1001-0548.2011.01.001.

[12] 吳定海， 張培林， 任國全， 等. 基于支持向量的單類分類方法綜述[J]. 計算機工程， 2011， 37（5）： 187-189. DOI： 10.3969/j.issn.1000-3428.2011.05.063.

WU D H， ZHANG P L， REN G Q， et al. Review of one-class classification method based on support vector[J]. Computer Engineering， 2013， 37（5）： 69-74. DOI： 10.3969/j.issn.1000-3428.2011.05.063.

[13] 趙志宏. 基于振動信號的機械故障特征提取與診斷研究[D]. 北京： 北京交通大學， 2012.