基于Simulink和VRML的球式自動平衡裝置虛擬實驗平臺研究

譚 青， 魏 來， 任志湘， 江 波

(中南大學 機電工程學院，長沙 410083)

?

基于Simulink和VRML的球式自動平衡裝置虛擬實驗平臺研究

譚 青， 魏 來， 任志湘， 江 波

(中南大學 機電工程學院，長沙 410083)

對球式自動平衡裝置虛擬實驗進行了研究，建立了球式自動平衡裝置虛擬實驗平臺。該平臺采用基于Simulink和VRML的運動仿真和建模方法，通過建立控制轉盤和滾球運動的Simulink模型，以及球式自動平衡裝置的VR場景，來模擬真實的實驗環境。然后在主界面上輸入實驗參數，以進行虛擬實驗。通過可視化觀察實驗過程中滾球運動狀態，以及生成的實驗結果曲線，對滾球的平衡過程進行分析，分析結果與自同期理論相符。最后通過搭建真實實驗臺進行實驗驗證，實驗結果進一步表明了該虛擬實驗平臺具有良好的有效性及可靠性。

球式自動平衡；虛擬實驗；Simulink；VRML；自同期

因轉子不平衡引起的振動和噪聲是回轉機械中最為常見的問題之一。解決這一問題的一般方法是對其回轉部分(即轉子)進行高精度的動靜平衡[1-3]。由此，學術界展開了自動平衡課題的研究。其中球式自動平衡裝置是根據柔性轉子和彈性支撐的特性,利用系統響應所形成的能量來驅動滾球的移動和分布,從而自動地消除轉子的不平衡。國內外研究均表明球式自動平衡裝置對于運動在過臨界轉速下的旋轉機械有較好的減振效益[4-8]。

虛擬實驗是以計算機為依托，借助于虛擬現實技術[9]和仿真軟件模擬實驗環境及過程的仿真實驗。利用虛擬現實技術進行的虛擬實驗具有科學性、可實現性、直觀性,交互性、可控性,可重復性、方便性和節省性等優點。隨著計算機技術和虛擬現實技術的迅速發展以及科學研究進一步深入的需要，虛擬實驗技術日益成熟和完善。

虛擬實驗的研究在發達國家已經十分普及，許多國家都進行了虛擬實驗的研究，并獲得了很多研究成果，文獻[10-11]中詳細介紹了虛擬實驗的相關概念及發展現狀。與此同時，還有許多大學與科研院所也開展了關于虛擬實驗的探索性研究，并獲取了很好的研究成果。如德國波鴻·魯爾大學研發的虛擬控制實驗室[12]，綜合應用多種插件和Java applet，該虛擬實驗的仿真和交互操作是采用MATLAB的工具庫Simulink[13]實現的，它的虛擬實驗場景采用虛擬現實建模語言VRML[14]編寫，用戶通過網絡信息瀏覽器使用該虛擬實驗室。該虛擬控制實驗室容納了多個經典的工程控制實驗，虛擬場景十分逼真，具有很好的交互性及可視化效果。又如清華大學的工程力學虛擬實驗室[15]，該虛擬實驗室依據力學的理論基礎和真實的實驗數據，進行力學的虛擬實驗，其實驗場景生動逼真，實驗內容豐富，且交互性強，并具有良好的人機交互界面。

在球式自動平衡技術以往的研究中存在著仿真及實驗過程不具有直觀性和交互性，對減振能力影響因素的分析過程不夠簡便，且在現有實驗條件下難以觀測滾球到達平衡位置的完整動態過程等問題。因此，需要一個高度仿真、易操作、交互性強、功能完善的球式自動平衡裝置虛擬實驗平臺。

本文提出一種基于Simulink和VR的球式自動平衡裝置虛擬實驗平臺，利用該平臺可方便的進行參數化虛擬仿真實驗，考察影響球式自動平衡裝置實現平衡的因素，并能觀測真實實驗中無法觀察到的滾球運動過程，具有良好的可視性及交互性，使球式自動平衡裝置的研究變得直觀、便捷。

1 球式自動平衡裝置的數學模型

球式自動平衡裝置的工作原理是轉子在過臨界轉速下旋轉時，轉子內滾球的位置將自動的受轉子機械振動相位的影響，移動到偏心質量的對面，在一定程度上抵消偏心質量所產生的離心慣性力，從而起到減振的作用。

球式自動平衡裝置的主要結構示意圖如圖1所示，轉盤固定在一根轉軸上，轉盤滾道內裝有若干滾球，其中轉盤中心位于O點，G處為不平衡質量，偏心距為e，滾球在半徑為R的滾道上運行。在建立數學模型時，將其結構簡化為轉盤和滾球兩部分，并做如下假設：

1) 轉盤為均質圓形薄盤；

2) 電機驅動力矩足夠大，轉速不會因阻力矩大小產生變化；

3) 球與滾道之間無相對滑動；

4) 轉盤處在水平方向，不考慮軸向運動及重力影響。

系統運動限制在XY平面內，剛度和阻尼簡化到水平和豎直方向上。

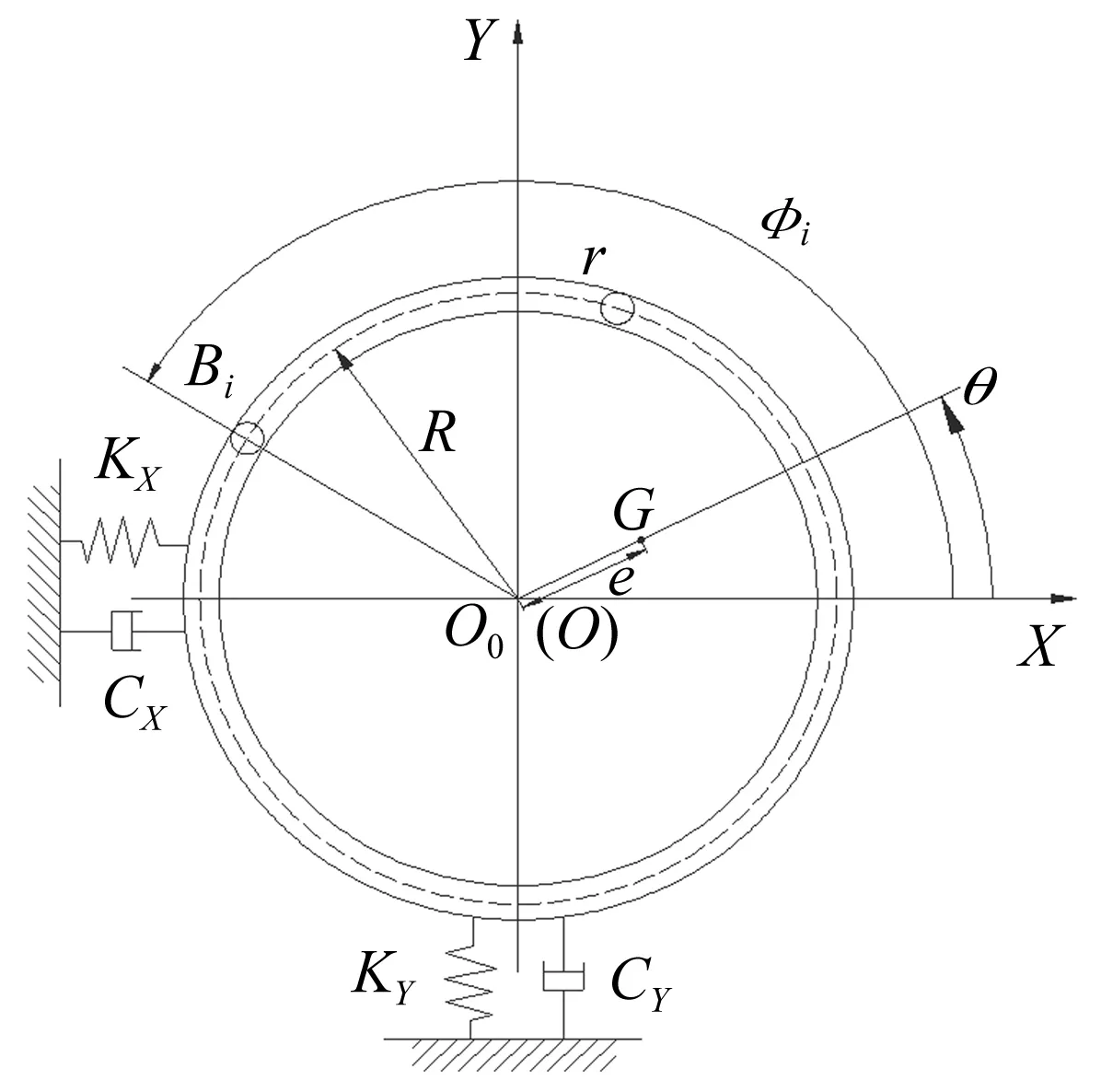
圖1 球式自動平衡裝置主要結構示意Fig.1 Main structure of the ball-type automatic balancer

文中符號的表示如下(單位均采用國際標準單位)：O0為坐標系的原點；O為轉盤的幾何中心(系統靜止時O和O0重合)；X、Y為轉盤中心O的坐標；Kx、KY為轉盤X方向的剛度系數、Y方向的剛度系數；CX、CY為轉盤X方向的黏性阻尼系數、Y方向的黏性阻尼系數；θ為不平衡質量相對于X軸的轉角；Φi為第i個滾球的轉角；Bi為第i個滾球的質心；β0為滾球的滾動摩擦因數；β1為滾球的黏性阻尼系數；m1、m2、m3、m分別為偏心質量、轉盤質量、電機質量、滾球質量；n為滾球個數；M為系統總質量(M=m1+m2+m3+nm)；I、I1、I2分別為滾球轉動慣量、偏心質量轉動慣量、圓盤轉動慣量；R、r分別為滾球轉動半徑、滾球半徑。

根據拉格朗日運動微分方程建立球式自動平衡裝置的數學模型，其推導過程參照文獻[16]第17～19頁，得到系統微分方程如下：

(1)

2 虛擬實驗平臺的基本框架

球式自動平衡裝置虛擬實驗平臺是一個利用計算機仿真軟件Simulink和VR虛擬現實技術模擬出球式自動平衡裝置實驗過程的平臺。

用戶可以根據實驗需求在基于MATLAB圖形用戶界面技術(GUI)設計的主界面上輸入相關參數(即設定實驗條件)，然后點擊相應的按鈕，虛擬實驗平臺中的球式自動平衡裝置便在用戶的控制下運行，用戶可看到接近真實的實驗環境，直觀地觀察到球式自動平衡裝置中轉盤和滾球的運動狀態，能隨時暫停實驗或用步進方式進行實驗，還可看到實時顯示的實驗裝置振幅曲線。實驗完畢，在主界面點擊相應按鈕，即可一鍵生成實驗結果，得到完整的振幅曲線，并可將實驗條件和實驗數據導出到表格文件以便進行數據后處理。這些功能使得平臺具有良好的交互性、實時性和靈活性。

平臺的實現采用模塊化的設計方法，將平臺的功能分成多個模塊，主要由主界面模塊、虛擬場景模塊、數值求解模塊、交互控制模塊四個功能模塊組成。功能模塊關系如圖2所示。

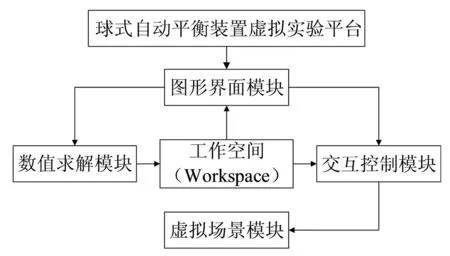
圖2 虛擬實驗平臺功能模塊關系Fig.2 Relationship between functional modules of virtual experiment platform

平臺的各個功能模塊之間是相互聯系的，其中工作空間(Workspace)是指MATLAB的基本工作空間，用來存儲數據變量。Simulink模型的所有參數默認調用基本工作空間中的數據，因此可以通過工作空間實現數據共享，將數值求解模塊計算的數據傳遞給Simulink模型。平臺的工作流程圖如圖3所示。

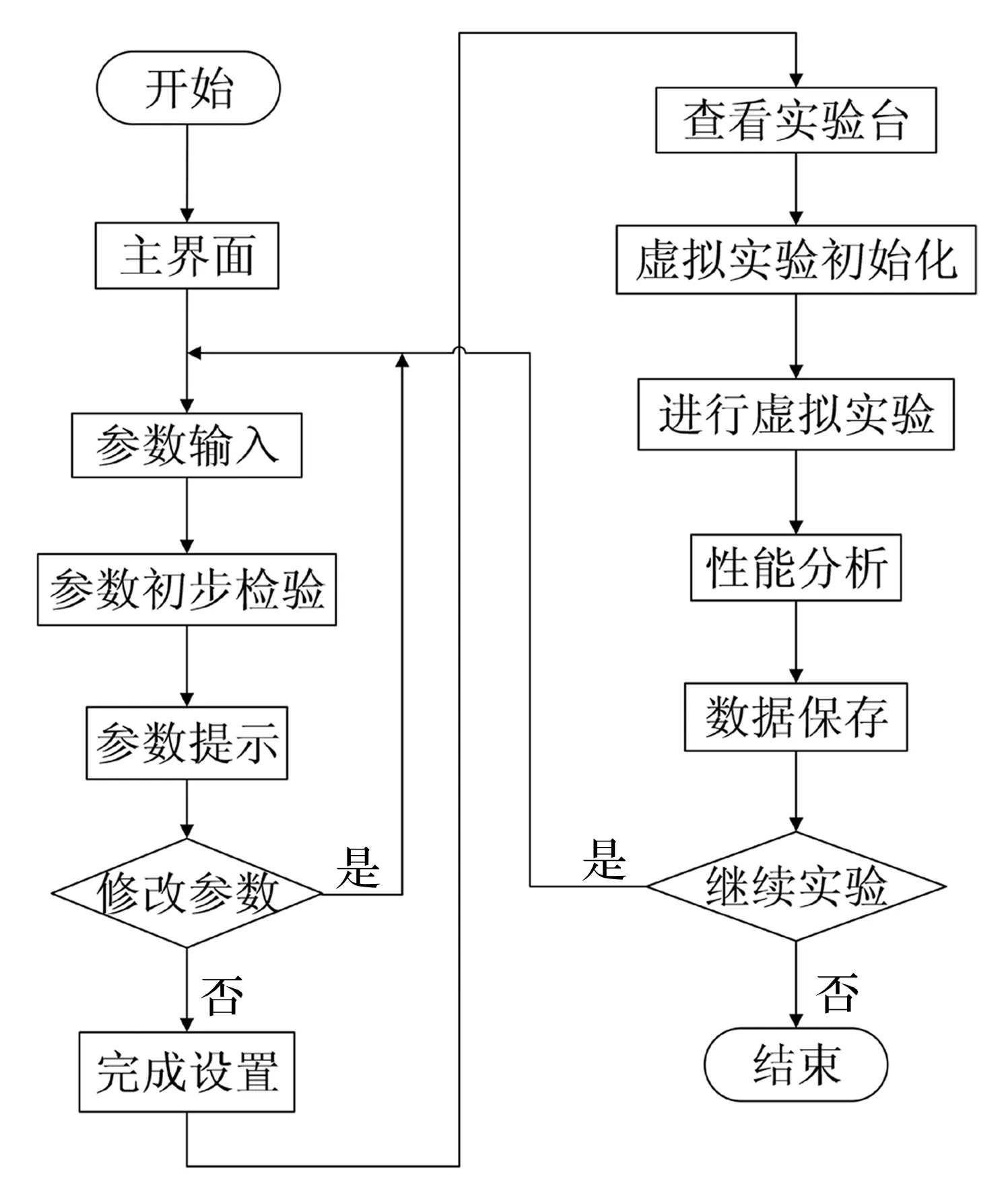
圖3 平臺工作流程Fig.3 Platform workflow

3 平臺功能模塊的設計與實現

3.1 主界面

主界面由三個面板(Panel)控件組成，對應將主界面分成三個區，分別是參數設置區、虛擬實驗控制區、通用功能區。界面的對象層次關系如圖4所示。

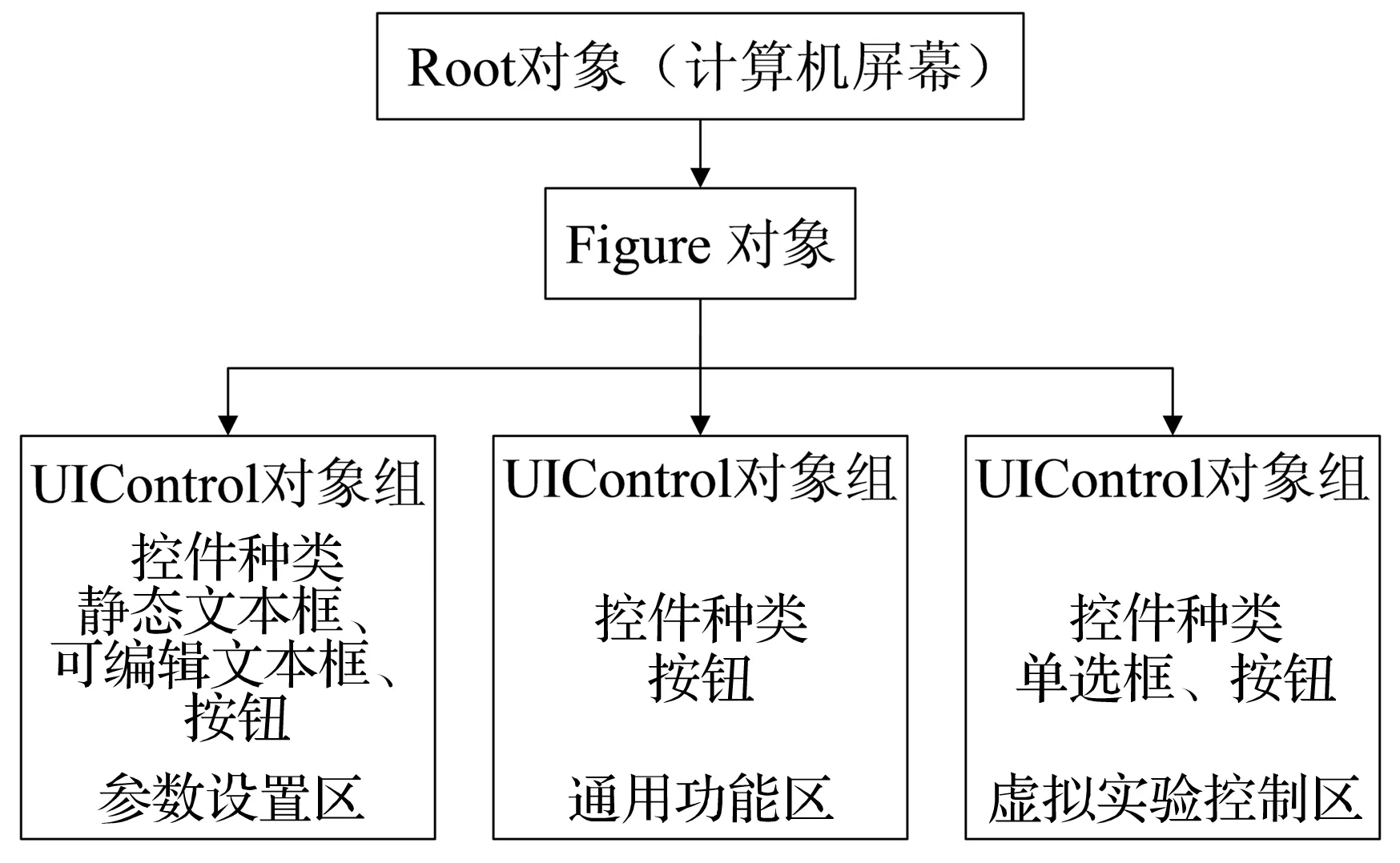
圖4 主界面對象層次結構Fig.4 User-interface object hierarchy

主界面模塊設計基于簡潔清晰、操作方便的設計思想，采用圖形化的界面，將參數設置模塊和通用功能模塊以及虛擬實驗控制模塊集中在界面上，避免用戶在操作過程中出現眾多界面導致的操作步驟繁瑣。

參數設置區用來輸入進行球式自動平衡裝置虛擬實驗所需要的條件，輸入的參數被M腳本程序所獲取用以進行運動微分方程的計算。

虛擬實驗控制區用來控制虛擬實驗的顯示模式及初始化、運行、暫停、繼續、停止、步進等功能。

通用功能區則用來實現虛擬實驗平臺的查看結果曲線、保存數據、重新實驗、退出系統等功能。

3.2 虛擬場景

虛擬場景模塊是虛擬實驗平臺中的重要功能模塊，它是實現虛擬實驗動態可視化的基礎。虛擬場景的模型由虛擬實驗室場景和虛擬實驗設備組成，本文采用虛擬現實建模語言VRML結合三維建模軟件Pro/E和3ds Max進行開發。

VRML是一種虛擬現實建模語言，用來創建真實世界的場景模型或人們所構想的虛擬世界，它具有平臺無關性。它克服了以往虛擬現實單一、交互性不強的缺點，將人的行動作為瀏覽虛擬場景的主體，為用戶創建了一個可融入的虛擬世界，虛擬世界由許多的原始對象按照一定的層次結構一級級地組織起來，構成各種復雜的場景，從而形成豐富多彩的虛擬世界，這便是構造虛擬世界的基本原理。

建立虛擬場景模型的步驟如下 ：① 利用Pro/E建立球式自動平衡實驗裝置的三維模型；② 利用3ds Max建立虛擬實驗室場景模型；③ 將Pro/E和3ds Max建立的模型導出為.wrl格式文件，然后把各個wrl文件在VRML編輯器中進行場景整合，并進行優化處理。

3.3 數值求解

3.3.1 仿真算法

機械系統的數學模型一般為微分方程或微分方程組，數值積分法中龍格-庫塔法是最為常用的數值計算方法，本實驗平臺的數值計算采用四階龍格-庫塔法。

對于通用格式的一階微分方程，如果初值可以確定，則借助微機可采用龍格-庫塔法求解。

如對下式所示初值問題：

(2)

采用四階龍格-庫塔法求解的遞推方法為：

(3)

式中:h為步長，ki為：

(4)

3.3.2 系統運動微分方程化簡

將球式自動平衡實驗裝置的系統微分方程式(1)化為適用于龍格-庫塔仿真算法通用格式的一階微分方程組。本實驗臺內置無球、單球、雙球、三球四種系統。以裝有三球的球式自動平衡裝置為例，介紹其降階化成通用的仿真格式方程的步驟。將實驗臺三球系統的數學模型進行降階處理，取：

S=[S1,S2,S3,S4,S5,S6,S7,S8,S9,S10]T=

將上式定義的廣義坐標代入式(1)得到式(5)：

(5)

3.3.3 碰撞處理

球式自動平衡裝置中的滾球在運動時可能會發生碰撞，在龍格-庫塔法的一個步求解后，需要檢查球的位置是否干涉，如果干涉，須做碰撞處理。

對于在滾道中運動的滾球，由于存在摩擦和黏性阻尼，數值仿真分析時可視為完全非彈性碰撞。

兩球碰撞的判斷條件為兩球夾角φ滿足:

φ<2arcsin(r/R)

(6)

當兩滾球碰撞時，兩球各移動的角度δ為：

δ=(2arcsin(r/R)-α)/2

(7)

兩球速度均變為：

(8)

滾球碰撞處理的示意圖如圖5所示。

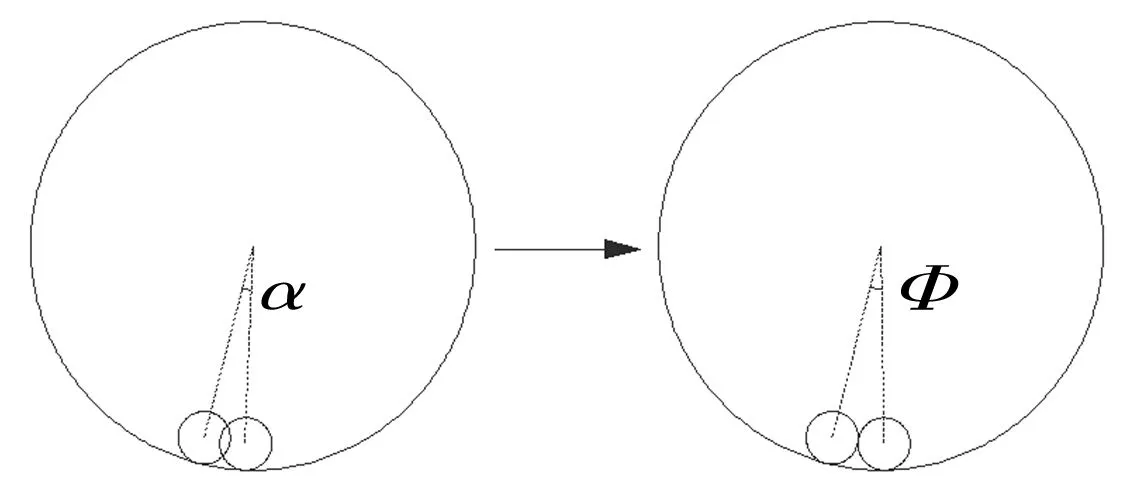
圖5 滾球碰撞示意Fig.5 Ball collision signal

3.4 交互控制

交互控制模塊主要是用來控制球式自動平衡裝置虛擬實驗過程動態可視化顯示，通過建立Simulink模型實現。模型通過Simulink中Gain模塊獲取輸入的初始條件滾球個數、滾球半徑等輸入參數，再結合AND和Switch等條件判斷選用合適的滾球，并將所選取的滾球在盤中的位置設置為主界面中輸入的初始位置。Simulink模型可以獲取數值求解模塊的計算結果，作為Simulink的信號源(Source)通過Simulink中VR Sink模塊輸出給VR虛擬場景中的相應節點，同時還可以獲取圖形界面輸入的初始條件與控制信號來控制虛擬實驗的進行。

該虛擬實驗平臺選用了三組不同大小的滾球，每組有三個,然后再分別建立每個滾球的rotation節點和translation節點的Simulink模型，以及轉盤rotation節點的Simulink模型，最后建立總Simulink模型。其中1號球rotation節點的Simulink模型及總Simulink模型如圖6所示。

Simulink模型建立后，設置仿真開始、結束時間，與數值求解程序中設置一致，仿真時間為0～50 s，仿真步長為定步長0.005，仿真算法采用ode4(四階龍格-庫塔法)。

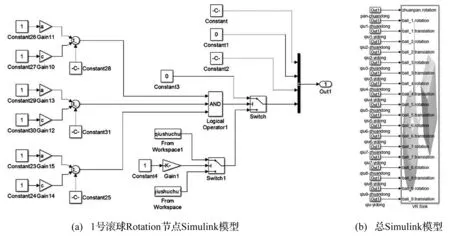
圖6 Simulink模型Fig.6 Simulink model

4 虛擬實驗平臺運行實例

在MATLAB環境中，進入用戶界面，同時打開虛擬實驗室場景，如圖7所示。用戶首先要在主界面上輸入實驗的初始條件，如滾動摩擦因數、黏性阻尼系數、偏心質量、滾球質量、滾球半徑、滾球個數、滾球的初始角度、穩態轉速等。

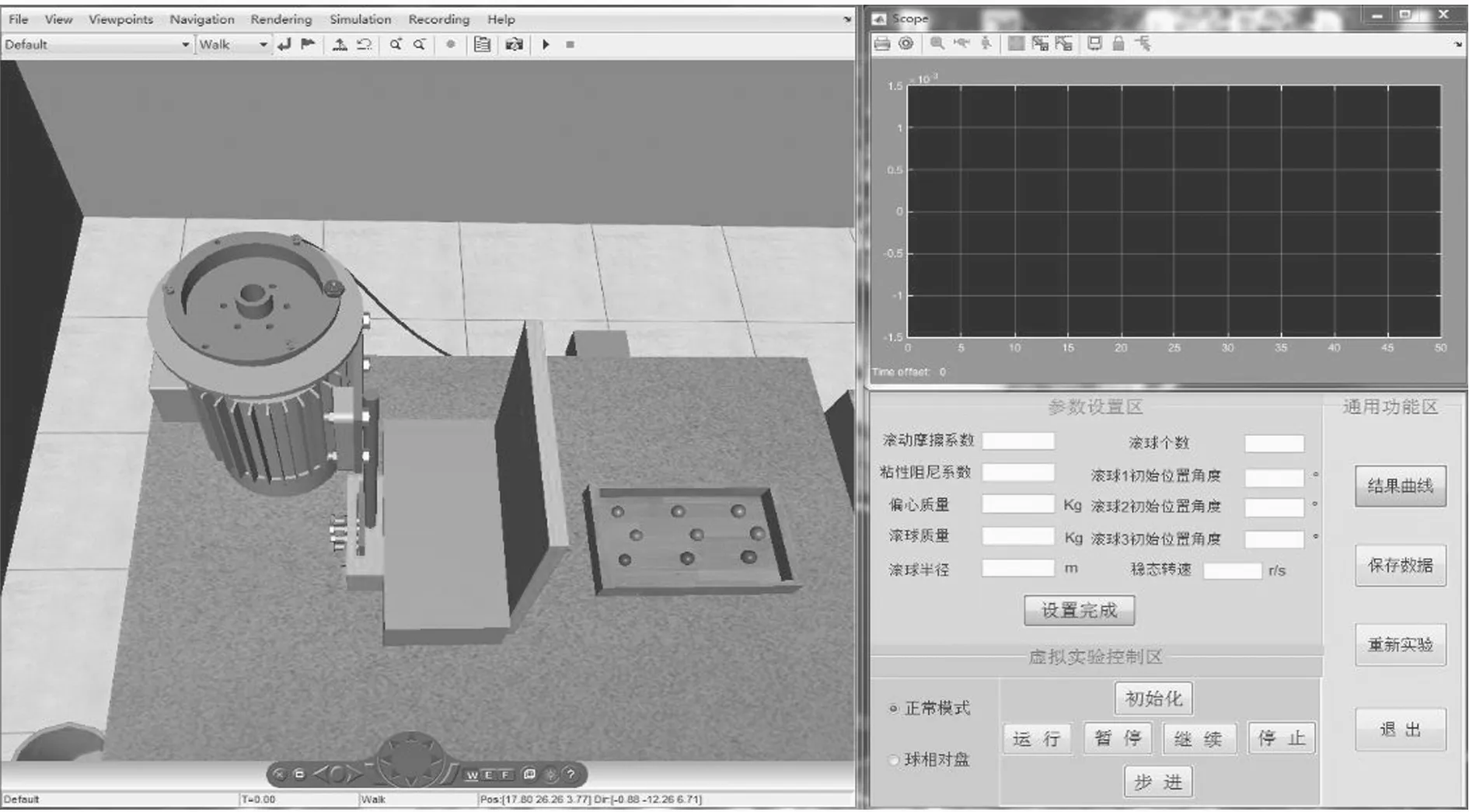
圖7 虛擬實驗平臺界面Fig.7 Interface of virtual experiment platform

實驗參數設置完畢后，在虛擬實驗控制區進行實驗運行模式的選擇，實驗運行模式有“正常模式”和“球相對盤”模式，默認為“正常模式”。“球相對盤”模式是將參考點固化在盤上，即轉盤不動、球相對于盤的視角模式，采用“球相對盤模式” 能夠以圓盤的角度觀察滾球相對盤運動情況，這在真實實驗中是無法觀察到的。

然后點擊虛擬實驗控制區的“初始化”按鈕，虛擬場景中的滾球便會按照用戶設置的滾球半徑與滾球個數自動選取球盒中的滾球，并按照用戶設置的滾球初始位置放置到轉盤中。再點擊“運行”按鈕，轉盤開始加速轉動，加速至電機穩態轉速后開始勻速轉動。實驗過程中，可以點擊“暫停”按鈕，查看當前滾球的運行位置，然后點擊“步進”按鈕可以放慢滾球的運動狀態，使其以步進方式運動，以便觀察其動態運動規律。點擊“暫停”或“步進”按鈕之后可以通過點擊“繼續”按鈕來恢復連續的運行狀態。最后，點擊“停止”按鈕，實驗裝置便停止運行。在平臺界面的右上角可以實時顯示轉盤的振幅曲線。

實驗完成后點擊“結果曲線”按鈕可以查看實驗結果，“結果曲線”界面如圖8所示。

下面分別用無滾球、2個滾球進行虛擬實驗以對球式自動平衡裝置虛擬實驗平臺進行驗證。實驗參數取值見表1。為了使仿真計算和實際情況一致，依據現實實驗中電機的穩態轉速為23.33 r/s，仿真中同樣設置電機轉速穩態值為23.33 r/s。

表1 實驗參數(未注單位為國際單位)

圖8 結果曲線Fig.8 Results

4.1 無滾球虛擬實驗

無滾球下的球式自動平衡裝置可視為普通不平衡轉子，從實驗結果的振幅曲線走向看出，剛開始由于轉速不大，轉子振幅較小，之后轉子轉速達到一階臨界轉速后通過共振區，達到最大振幅，最后逐漸衰減為穩定值。在結果曲線界面中，放大曲線圖可觀察到最大振幅發生在1.8 s左右，此時的轉速為9 r/s，此轉速即為一階臨界轉速。最大振幅值和殘留振幅值如下(水平方向最大振幅由Ymax表示，殘留振幅由Ybal表示)。

Ymax=1.07×10-3m,Ybal=9.63×10-5m

未裝滾球虛擬實驗結果如圖9所示。

4.2 2個滾球虛擬實驗

球式自動平衡裝置內裝有2個滾球，滾球與偏心質量的初始夾角分別為90°和180°，通過對滾球運動過程及對轉子實時振幅的觀察可知， 剛開始由于轉速不

圖9 未裝滾球虛擬實驗結果(Y方向振幅曲線)Fig.9 Virtual experiment results of 0 ball(The Y direction curve of amplitude)

大，轉子振幅較小，之后轉子轉速達到一階臨界轉速后通過共振區，達到最大振幅，該振幅超過了不裝滾球時的最大振幅，通過對該階段實驗過程進行步進觀察，發現轉子達到最大振幅時，滾球位置是在不平衡質量的一側，說明此時滾球加大了不平衡量，最后振幅逐漸衰減為一個穩定值，該穩定值遠低于未裝滾球時的殘留振幅，說明滾球已經起到平衡不平衡質量的作用，減振效果明顯，符合自同期現象[12]。最大振幅值和殘留振幅值具體數據如下：

Ymax=2.01×10-3m,Xbal=1.47×10-6m

滾球1和滾球2與偏心質量最后的夾角分別為120.64°和241.04°，此時的不平衡量為1.17×10-5kg·m。球式自動平衡裝置裝有2個滾球的實驗結果曲線如圖10所示。

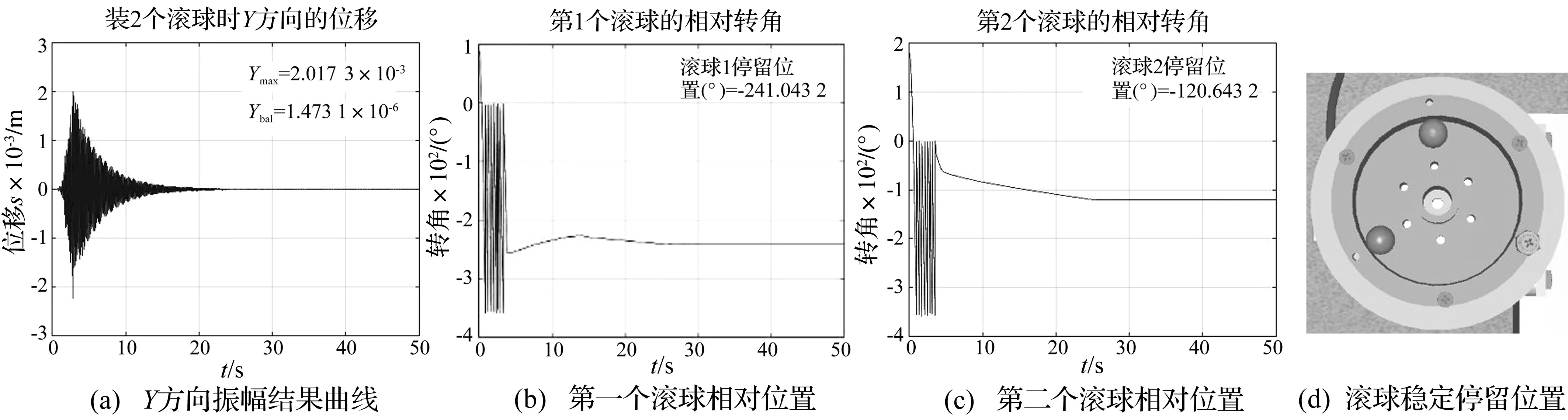
圖10 2個滾球虛擬實驗結果Fig.10 Virtual experiment results of 2 balls

5 真實實驗驗證

為進一步驗證虛擬實驗平臺的有效性及可靠性，采用如圖11所示實驗方案進行真實實驗驗證。

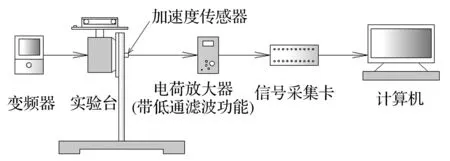
圖11 真實實驗方案Fig.11Real experiment program

在此方案中，由實驗條件可計算出實驗臺的臨界轉速為8.2 r/s。開始實驗時，首先裝入所需數量的滾球，用變頻器調好需要的穩態轉速(本實驗中為23.33 r/s)，然后開機讓電機自然加速，到達穩態轉速后繼續運行一段時間，最后關機停止運行，總時長計30 s(根據經驗，這段時間足以使滾球達到穩定狀態)，并在電腦上對實驗過程中通過信號采集卡采集到的數據進行分析。

圖12 真實實驗臺Fig.12 The real test-bed

實驗裝置如圖12所示,由1底座、2彈性支撐桿、3電動機、4連接轉盤、5轉盤和6變頻器組成。電動機通過螺栓連接到支撐桿連接板上。支撐桿為材質均勻的45號鋼。為滿足實驗需求，選用的變頻器型號為SAJ8000-M，工作電壓為220 V，功率為0.4 kW。本實驗裝置中，由于主軸直徑較大且伸出的長度較小，認為電機轉子和主軸的剛性遠大于彈性支撐桿2，因此本文中把圓盤和主軸看做是一個盤狀剛體。此外，為了減少因安裝電機的鐵架結構較薄弱而產生的振動，在鐵架的底部放置如圖12中所示鐵塊及人工加壓來增加鐵架結構的穩定程度。由于實驗條件所限，實驗中轉盤會因不能保持水平而產生振動分量，但因其量值較小，本文認為可忽略不計，另外根據國內外文獻，這種處理方法也是常見的。

下面分別在未裝滾球和裝有2個滾球情況下進行真實實驗驗證，真實實驗參數與虛擬實驗參數相同。

5.1 未裝滾球真實實驗

圖13所示為轉子在未裝滾球時從開機到穩定狀態的真實實驗結果。觀察實驗結果可知，開機后，亞臨界轉速時振動逐漸加劇，振幅比較大；經過轉子系統的共振區時達到了最大振幅值；在過臨界轉速時轉子進入穩定振動狀態，振動減弱，振幅值為一穩定值。通過放大觀察真實實驗振動曲線圖可知最大振幅發生在實驗開始后1.7 s左右，此時電機轉速為8.5 r/s，此轉速即為一階臨界轉速，轉速值與虛擬實驗結果相符。最大振幅為1.10×10-3m，穩態振幅為7.60×10-4m。

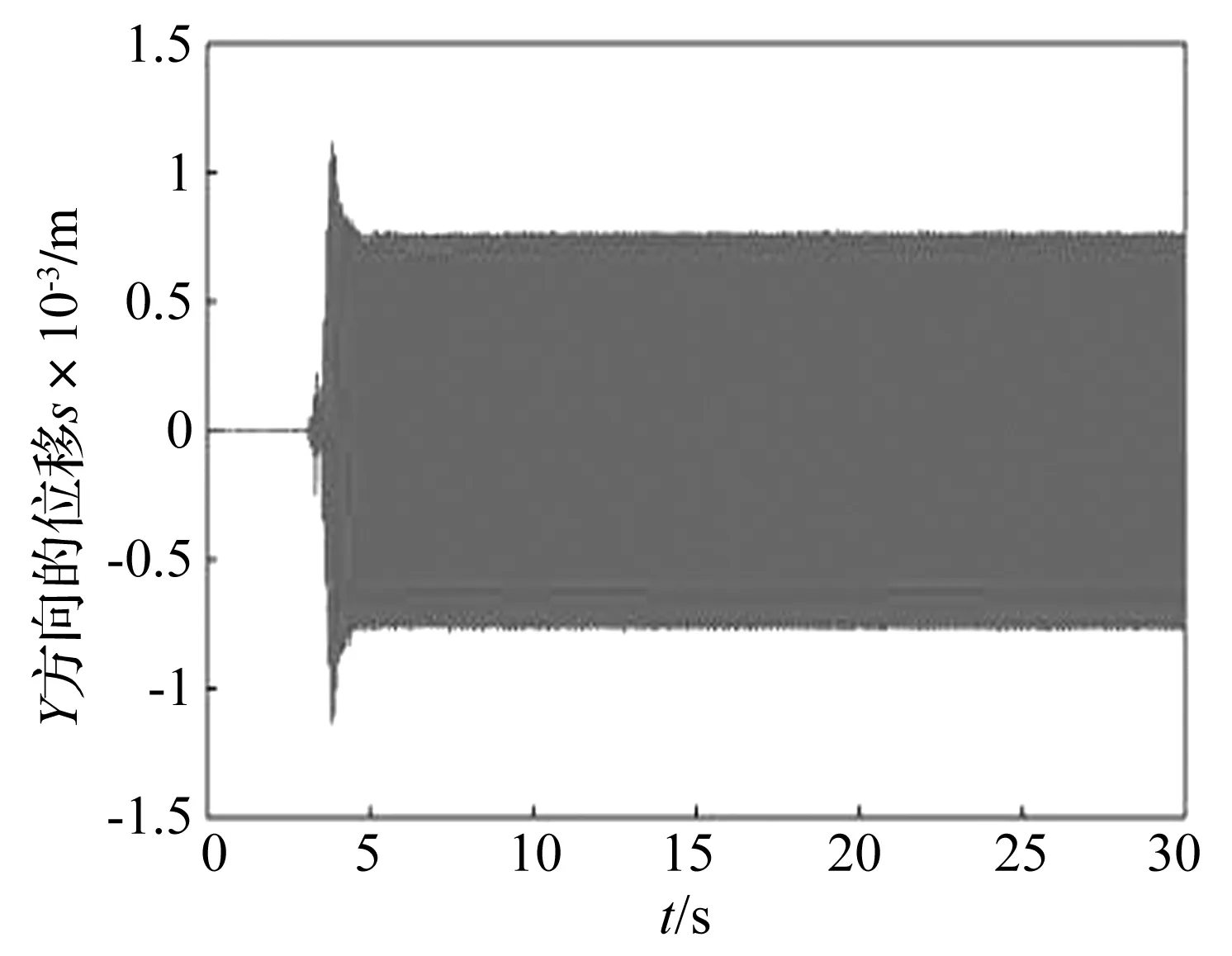
圖13 未裝滾球真實實驗結果(Y方向振幅曲線)Fig.13 Real experiments results of 0 ball (the Y direction curve of amplitude)

5.2 裝2個滾球真實實驗

圖14所示為轉子在裝有2個滾球作用下從開機到穩定狀態的實驗結果。觀察實驗結果可知，開機后，亞臨界轉速時，2個滾球均偏向偏心質量一邊，使不平衡加劇，從而增大了振幅，裝有2個滾球的最大振幅為1.40×10-3m，比未裝滾球時大。過臨界轉速時滾球運動到偏心質量對面，使得不平衡減弱，穩態振幅減小。裝有2個滾球的穩態振幅為2.20×10-4m，比未裝滾球時小。滾球最終的穩定停留位置處在偏心質量對面，與偏心質量夾角分別為119°、237°，此時的不平衡量為3.25×10-5kg·m，與虛擬實驗中的不平衡量相符。實驗結果表明，裝有2個滾球時轉子在亞臨界轉速時振幅增大，而在過臨界轉速時，與未裝滾球的轉子相比較實現了較好的減振效果。

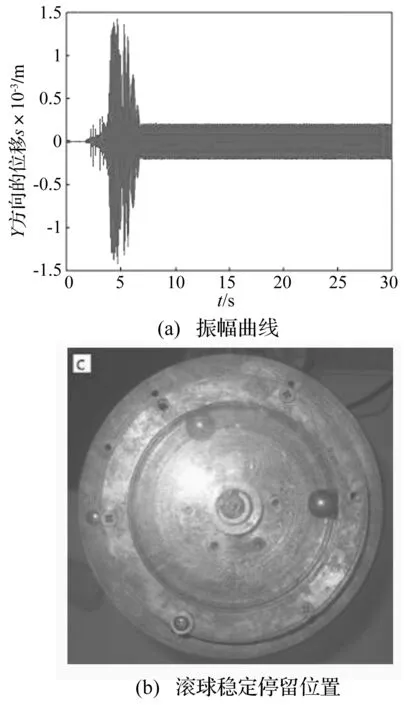
圖14 2個滾球真實實驗結果Fig.14 Real experiments results of 2 balls

6 結 論

(1) 本文通過仿真軟件Simulink及虛擬現實建模語言VRML建立了一個球式自動平衡裝置虛擬實驗平臺，為球式自動平衡裝置的研究提供了一種新方法。

(2) 通過在虛擬實驗平臺主界面上輸入實驗參數，可以便捷的生成結果曲線和數據等準確的實驗結果，從而對實驗結果進行分析。通過可視化觀察實驗過程中滾球運動狀態，從而對滾球的平衡過程進行研究，并可在實驗過程中實時顯示轉盤的振幅，實現了球式自動平衡裝置實驗過程的動態可視化。

(3) 通過未裝滾球和裝有2個滾球的虛擬實驗及真實實驗驗證，得到的實驗結果與自同期理論一致，不平衡轉子的振幅均得到了有效衰減，從而證明了該虛擬實驗平臺的有效性與可靠性。

(4) 該虛擬實驗平臺采用模塊化設計，具有交互性強、功能模塊清晰、易于擴充等特點，能為以Simulink和VRML為基礎開發其他虛擬實驗平臺提供很好的參考模型。

[1] 潘鑫,吳海琦,高金吉. 轉子-軸承系統液體式在線自動平衡裝置研究綜述[J]. 振動與沖擊,2015,34(6):95-100.

PAN Xin, WU Haiqi, GAO Jinji. Review for liquid-typed online auto-balancing devices in rotor-bearing systems [J]. Journal of Vibration and Shock, 2015, 34(6):95-100.

[2] 汪希萱,曾勝. 電磁式在線自動平衡系統及其動平衡方法研究[J]. 熱能動力工程,2003,18(1):53-57.

WANG Xixuan, ZENG Sheng. Electromagnetic online auto balance system and research of its dynamic balance method [J]. Journal of Engineering for Thermal Energy and Power, 2003, 18(1): 53-57.

[3] 魏彤,向岷. 磁懸浮高速轉子基于位移剛度力超前前饋補償的高精度自動平衡方法[J]. 機械工程學報,2012,48(16):184-191.

WEI Tong, XIANG Min. Autobalancing for magnetically suspended high-speed rotors based on lead feedforward compensation for displacement stiffness force [J]. Journal of Mechanical Engineering, 2012,48(16): 184-191.

[4] 譚青，周鐵，黃秀祥. 球式自動平衡裝置的數值仿真與實驗研究[J]. 噪聲與振動控制，2008，28(3)：142-145.

TAN Qing, ZHOU Tie, HUANG Xiuxiang. Numerical simulation and experimental study of automatic ball balancer[J]. Noise and Vibration Control，2008，28(3)：142-145.

[5] RAJALINGHAM C, BHAT R B. Complete balancing of a disk mounted on a vertical cantilever shaft using a two ball automatic balancer [J]. Journal of Sound and Vibration, 2006, 290(1/2):169-191.

[6] LU C J, HUNG C H. Stability analysis of a three-ball automatic balancer [J]. Journal of Vibration and Acoustics, 2008, 130(5):786-791.

[7] LU C J. Stability analysis of a single-ball automatic balancer [J]. Journal of Vibration and Acoustics, 2006, 128(1): 122-125.

[8] SUNG C K, CHAN T C, CHAO C P, et al. Influence of external excitations on ball positioning of an automatic balancer[J]. Mechanism and Machine Theory, 2013, 69: 115-126.

[9] 鄒湘軍,孫健,何漢武,等. 虛擬現實技術的演變發展與展望[J]. 系統仿真學報,2004(9):1905-1909.

ZOU Xiangjun, SUN Jian, HE Hanwu, et al. The development and prospects of virtual reality[J]. Journal of System Simulation,2004(9):1905-1909.

[10] HUGO J. On the use of VRML in educational software Experiences from the project: JIMM problem solver[J].Future Generation Computer Systems，2000，17(1): 49-56.

[11] WEYRICH M, DREWS P. Virtual reality for design and management: the virtual workbench [J]. Computers in Industry, 1999,38 (4): 5-15.

[12] Ruhr-Universitat. Virtual Control Lab [EB/OL]. http://www.atp.ruhr-uni-bochum.de/VCLab/[1996-11-12].

[13] 陳永盛,吳斌,王貞,等. 基于Simulink的混合試驗系統其驗證[J]. 振動與沖擊,2014,34(7):18-23.

CHEN Yongsheng, WU Bin, WANG Zhen, et al. Simulation and validation of a hybrid testing system with Simulink[J]. Journal of Vibration and Shock, 2014,34(7): 18-23.

[14] 師黎,王治忠,費敏銳. 基于VRML與MATLAB的智能控制虛擬實驗室設計與實現[J]. 儀器儀表學報,2008,29(12):2594-2598.

SHI Li, WANG Zhizhong, FEI Minrui. Design and implementation of an intelligent control virtual laboratory based on VRML and MATLAB [J]. Chinese Journal of Scientific Instrument,2008,29(12):2594-2598.

[15] 清華大學.工程力學虛擬實驗室[EB/OL]. http://jwc.henau.edu.cn/resource/thcw/j53/, 2001. Tsinghua University. Virtual laboratory for engineering mechanics [EB/OL]. http://jwc.henau.edu.cn/resource/thcw/j53/, 2001.

[16] 周鐵. 內裝滾球轉子自同期現象的理論與實驗研究[D].長沙: 中南大學,2008.

A virtual experiment platform of a ball-type automatic balancer based on Simulink and VRML

TAN Qing, WEI Lai, REN Zhixiang, JIANG Bo

(College of Mechanical & Electrical Engineering, Central South University, Changsha 410083, China)

Virtual experiment of a ball-type automatic balancer was studied and a virtual experiment platform of the ball-type automatic balancer was built. The platform simulated a real experiment environment by establishing Simulink models of plates’ and balls’ movement, and VR scene of the ball-type automatic balancer, based on Simulink motion simulation and VRML (virtual reality modeling language) modeling methods. Then parameters were input in the main interface to conduct virtual experiments. Through visual observation of ball’s state in the experiment and experimental results, we could analyze equilibrium process of balls. The results of the analysis are consistent with the theory of self-synchronizing. Finally, the experiments on real test-bed indicate that the virtual experimental platform has good validity and reliability.

virtual experiment; ball-type automatic balancer; Simulink; virtual reality modeling language (VRML); self-synchronizing

國家自然科學基金(51274252)

2015-08-11 修改稿收到日期：2015-10-26

譚青 男，博士，教授，博士生導師，1955年生

魏來 男，碩士生，1990年生

TH113.1;TP311

A

10.13465/j.cnki.jvs.2016.20.001