理清概念掌握運算透視考點
賈蕓蕓
理清概念掌握運算透視考點
賈蕓蕓
在初中數學中,“數與式”是“數與代數”領域的重要基礎內容,它包括:有理數、實數、代數式、整式、分式等.這部分內容有如下的突出特點:知識點多,技能性強,體現轉化思想和類比方法多,因此是中考重要考點之一,一般以選擇題、填空題和簡單的解答題出現.中考考查的重點是概念,運算量不大.現把2015年全國各地數與式中常見的考點歸納如下.
考點一:相反數、絕對值、倒數的相關概念
例1(2015·黔南州)下列說法錯誤的是().
A.-2的相反數是2
C.(-3)-(-5)=2
D.-11,0,4這三個數中最小的數是0
【考點】相反數;倒數;有理數的減法;有理數大小比較.
【分析】根據相反數的概念、倒數的概念、有理數的減法法則和有理數的大小比較進行判斷即可.
解:-2的相反數是2,A正確;
(-3)-(-5)=-3+5=2,C正確;
-11,0,4這三個數中最小的數是-11,D錯誤.故選D.
【點評】本題考查的是相反數的概念、倒數的概念、有理數的減法法則和有理數的大小比較,掌握相關概念和法則是解題的關鍵.
考點二:無理數的概念
A.4B.2C.1D.3
【考點】無理數.
【分析】掌握無理數的三種形式:①開方開不盡的數,②無限不循環小數,③含有π的數,結合題意判斷即可.
【點評】此題主要考查了無理數的定義,熟記無理數的三種形式是解題關鍵.
考點三:實數與數軸
例3(2015·棗莊)實數a,b,c在數軸上對應的點如圖1所示,則下列式子中正確的是().

圖1
A.ac>bc
B.a-b=a-b
C.-a<-b<c
D.-a-c>-b-c
【考點】實數與數軸.
【分析】先根據各點在數軸上的位置比較其大小,再對各選項進行分析即可.
解:∵由圖1可知,a<b<0<c,
∴ac<bc,故A選項錯誤;
∵a<b,∴a-b<0,∴a-b=b-a,故B選項錯誤;
∵a<b<0,∴-a>-b,故C選項錯誤;
∵-a>-b,c>0,∴-a-c>-b-c,故D選項正確.故選D.
【點評】本題考查的是實數與數軸,熟知數軸上各點與實數是一一對應關系是解答此題關鍵.
例4(2015·資陽)如圖2,已知數軸上的點A、B、C、D分別表示數-2、1、2、3,則表示數的點P應落在線段().
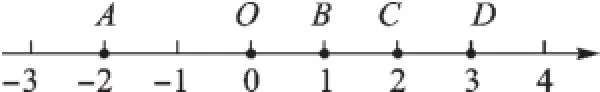
圖2
A.AO上B.OB上
C.BC上D.CD上
【考點】估算無理數的大小;實數與數軸.
故選B.
考點四:科學記數法
例5(2015·鹽城)火星與地球的距離約為56 000 000千米,這個數據用科學記數法表示為__________千米.
【考點】科學記數法.
【分析】科學記數法的表示形式為a×10n的形式,其中1≤a<10,n為整數.確定n的值時,要看把原數變成a時,小數點移動了多少位,n的絕對值與小數點移動的位數相同.當原數絕對值>1時,n是正數;當原數的絕對值<1時,n是負數.
解:將56 000 000用科學記數法表示為5.6×107.故答案為:5.6×107.
【點評】此題考查科學記數法的表示方法.科學記數法的表示形式為a×10n的形式,其中1≤a<10,n為整數,表示時關鍵要正確確定a的值以及n的值.
考點五:數的開方與二次根式
例6(2015·南京)4的平方根是______;4的算術平方根是______.
【考點】算術平方根;平方根.
【分析】如果一個非負數x的平方等于a,那么x是a的算術平方根,由此即可求出結果.
解:4的平方根是±2;4的算術平方根是2.故答案為:±2;2.
【點評】此題主要考查了平方根和算術平方根的概念,算術平方根易與平方根的概念混淆而導致錯誤.
A.x≠1B.x≥1
C.x>1D.x≥0
【考點】二次根式有意義的條件.
【分析】先根據二次根式有意義的條件列出關于x的不等式,求出x的取值范圍即可.
【點評】本題考查的是二次根式有意義的條件,熟知二次根式具有非負性是解答此題的關鍵.
【考點】非負數的性質:算術平方根;非負數的性質:偶次方.
【分析】根據非負數的性質可求出m、n的值,進而可求出(m+n)5的值.
解:由題意知,m,n滿足(m-1)2+=0,∴m=1,n=-2,∴(m+n)5=(1-2)5=-1.故答案為:-1.
【點評】此題主要考查了非負數的性質,初中階段有三種類型的非負數:①絕對值;②偶次方;③二次根式(算術平方根).當它們相加和為0時,必須滿足其中的每一項都等于0.根據這個結論可以求解這類題目.
考點六:代數式、整式、分式
例9(2015·揚州)若a2-3b=5,則6b-2a2+2015=_______.
【考點】代數式求值.
【分析】首先根據a2-3b=5,求出6b-2a2的值是多少,然后用所得的結果加上2015即可.
解:6b-2a2+2015=-2(a2-3b)+2015=-2× 5+2015=-10+2015=2005.
答案:2005.
【點評】此題主要考查了代數式的求值問題,采用代入法即可,要熟練掌握.題型簡單總結有以下三種:①已知條件不化簡,所給代數式化簡;②已知條件化簡,所給代數式不化簡;③已知條件和所給代數式都要化簡.
例10(2015·本溪)下列運算正確的是().
A.5m+2m=7m2
B.-2m2·m3=2m5
C.(-a2b)3=-a6b3
D.(b+2a)(2a-b)=b2-4a2
【考點】冪的乘方與積的乘方;合并同類項;單項式乘單項式;平方差公式.
【分析】A.依據合并同類項法則計算即可;B.依據單項式乘單項式法則計算即可;C.依據積的乘方法則計算即可;D.依據平方差公式計算即可.
解:A.5m+2m=(5+2)m=7m,故A錯誤;
B.-2m2·m3=-2m2+3=-2m5,故B錯誤;
C.(-a2b)3=-a6b3,故C正確;
D.(b+2a)(2a-b)=(2a+b)(2a-b)=4a2-b2,故D錯誤.故選C.
【點評】本題主要考查的是整式的計算,掌握合并同類項法則、單項式乘單項式法則、積的乘方法則以及平方差公式是解題的關鍵.
A.2或-1B.0
C.2D.-1
【考點】分式的值為零的條件.
【分析】分式的值為0的條件是:(1)分子為0;(2)分母不為0.兩個條件需同時具備,缺一不可.據此可以解答本題.
解:由題意可得:x-2=0且x+1≠0,
解得x=2.故選C.
【點評】此題主要考查了分式值為零的條件,關鍵是掌握分式值為零的條件是分子等于零且分母不等于零.注意:“分母不為零”這個條件不能少.
考點七:因式分解
例12(2015·畢節)下列因式分解正確的是().
A.a4b-6a3b+9a2b=a2b(a2-6a+9)
B.x2-x+
C.x2-2x+4=(x-2)2
D.4x2-y2=(4x+y)(4x-y)
【考點】因式分解:運用公式法;提公因式法.
【分析】原式各項分解得到結果,即可做出判斷.
解:A.原式=a2b(a2-6a+9)=a2b(a-3)2,錯誤;
C.原式不能分解,錯誤;
D.原式=(2x+y)(2x-y),錯誤,故選B.
【點評】此題考查了因式分解的運用公式法以及提公因式法,熟練掌握因式分解的方法是解本題的關鍵.
考點八:數字規律探索
例13(2015·臨沂)觀察下列關于x的單項式,探究其規律:x,3x2,5x3,7x4,9x5,11x6,…,按照上述規律,第2015個單項式是().
A.2015x2015B.4029x2014
C.4029x2015D.4031x2015
【考點】單項式;規律型.
【分析】系數的規律:第n個對應的系數是2n-1;
指數的規律:第n個對應的指數是n.
解:根據分析的規律,得
第2015個單項式是4029x2015.故選C.
【點評】此題考查單項式問題,分別找出單項式的系數和次數的規律是解決此類問題的關鍵.
(作者單位:江蘇省淮安外國語學校)

