寬帶束離子注入機均勻性調(diào)節(jié)與控制方法研究

彭立波，鐘新華，張賽，張進學(xué)

（中國電子科技集團公司第四十八研究所，湖南長沙，410111）

寬帶束離子注入機均勻性調(diào)節(jié)與控制方法研究

彭立波，鐘新華，張賽，張進學(xué)

（中國電子科技集團公司第四十八研究所，湖南長沙，410111）

寬帶束離子注入機的均勻性調(diào)節(jié)系統(tǒng)由線圈磁鐵組及可調(diào)磁極組組成，通過分析調(diào)節(jié)原理，結(jié)合實際調(diào)試中獲得的可調(diào)磁極組中單個磁極調(diào)節(jié)的束流均勻性影響曲線，擬合曲線，建立束流均勻性影響模型，進一步推導(dǎo)出調(diào)節(jié)模型。在實際應(yīng)用中，設(shè)計合理的控制方法，根據(jù)束流的實際情況，采用內(nèi)/外插值法，適時調(diào)節(jié)束流均勻性影響模型參數(shù)組，可改善模型的適應(yīng)性。經(jīng)過測試表明，采用基于束流均勻性調(diào)節(jié)模型的迭代調(diào)節(jié)方法，可實現(xiàn)束流均勻性調(diào)節(jié)，測試注入300 mm硅片的方塊電阻均勻性達到1.17%。

寬帶束；離子注入機；均勻性調(diào)節(jié)；迭代算法

離子注入劑量均勻性與重復(fù)性是注入工藝最重要的指標之一，直接影響到器件性能的一致性和成品率［1-3］，對于采用水平寬帶束配合垂直一維機械掃描方式進行離子注入的大束流寬帶束離子注入機，寬度方向束流均勻性與離子源、各束線光路單元的工作參數(shù)及其穩(wěn)定性等很多因素密切相關(guān)，且直接影響離子注入劑量的均勻性，需設(shè)計恰當?shù)氖骶鶆蛐哉{(diào)節(jié)系統(tǒng)，并研究高效的調(diào)節(jié)控制算法，才能滿足離子注入工藝的要求。

1　離子束線系統(tǒng)簡介

寬帶束的束流均勻性調(diào)節(jié)系統(tǒng)如圖1所示，線圈磁鐵組、可調(diào)磁極組與平行透鏡磁極均在垂直方向以寬帶離子束平面對稱設(shè)置，在垂直方向形成磁場。其中線圈磁鐵組與可調(diào)磁極組構(gòu)成調(diào)節(jié)主體，線圈磁鐵組的磁場由各線圈電流共同產(chǎn)生，通過調(diào)節(jié)各線圈的電流改變局部磁場強度；可調(diào)磁極組屬于平行透鏡磁極的一部分，磁場由平行透鏡線圈產(chǎn)生，每個磁極在垂直方向位置可調(diào)，即磁極距可調(diào)，當平行透鏡線圈電流設(shè)定后，調(diào)節(jié)每單個磁極的磁極距，局部磁場強度發(fā)生改變。寬帶離子束中通過線圈磁鐵組發(fā)生電流調(diào)整的磁極區(qū)域或可調(diào)磁極組發(fā)生磁極距調(diào)整的磁極區(qū)域的部分離子束的傳輸方向產(chǎn)生相應(yīng)變化，最終束流在靶臺平面的均勻性分布也產(chǎn)生相應(yīng)的變化。

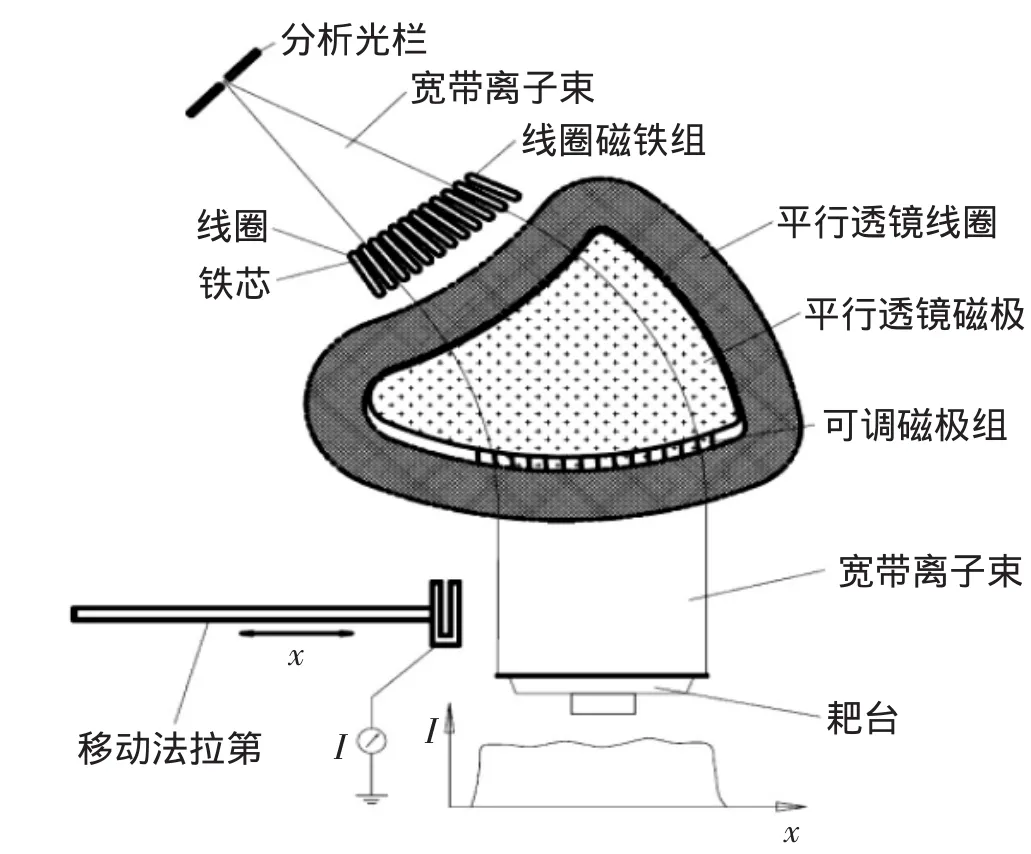
圖1　束流均勻性調(diào)節(jié)系統(tǒng)

移動法拉第用于束流在水平方向分布均勻性測量。移動法拉第水平勻速移動，對寬帶離子束進行掃描采樣，以靶臺為中心對稱取340 mm寬的束流數(shù)據(jù)，形成束流均勻性數(shù)據(jù)，求標準方差σ與束流平均值I的比值即為束流均勻性參數(shù)值。

線圈磁鐵組距離靶臺較遠，較小的水平角度偏移能在靶臺位置產(chǎn)生較大的束流均勻性分布變化，同時，線圈磁鐵組所處位置的束流處于擴張區(qū)，水平尺寸較小，限制了線圈磁鐵組有效調(diào)節(jié)線圈的數(shù)量，不利于對束流均勻性進行精細調(diào)節(jié)，用于粗調(diào)；可調(diào)磁極組距離靶臺位置較近，處于束流最寬位置，有效調(diào)節(jié)磁極數(shù)量較多，用于細調(diào)，完成主要的均勻性調(diào)節(jié)功能。

2　束流均勻性調(diào)節(jié)系統(tǒng)建模與參數(shù)優(yōu)化

寬帶束離子注入機完成初步束流調(diào)節(jié)后，在基本能量、電流、有效束寬度、初始束流均勻性達到基本要求，開始進行束流均勻性調(diào)節(jié)，調(diào)節(jié)流程如圖2。調(diào)節(jié)分兩步進行，第一步調(diào)節(jié)線圈磁鐵組，使束流均勻性指標達到一初始值；第二步調(diào)節(jié)可調(diào)磁極組，束流均勻性指標達到目標值。

根據(jù)當前束流均勻性數(shù)據(jù)，基于調(diào)節(jié)模型獲得優(yōu)化的線圈磁鐵組的12對線圈的電流值和可調(diào)磁極組的14對磁極極距值，是束流均勻性調(diào)節(jié)算法的核心。線圈磁鐵組和可調(diào)磁極組對束流均勻性影響的基本原理相同，在模型中可通過替代相應(yīng)的變量，實現(xiàn)算法的轉(zhuǎn)移，因此本文只對可調(diào)磁極組的磁極距參數(shù)優(yōu)化算法進行介紹。

經(jīng)過實際調(diào)試發(fā)現(xiàn)可調(diào)磁極組每單個磁極對束流的均勻性分布影響有一定規(guī)律，經(jīng)過現(xiàn)場調(diào)試收集束流均勻性數(shù)據(jù)，獲得如圖3所示的束流均勻性影響曲線。曲線數(shù)據(jù)為：

xn為移動法拉第沿x軸移動檢測的第n個位置；I0（xn）為多磁極極距調(diào)整前該位置的束流值；I1（xn）為多磁極極距調(diào)整后相同位置的束流值。

對以上曲線進行擬合，得到式（2）的分布函數(shù)

圖2　束流均勻性調(diào)節(jié)流程

將可調(diào)磁極組的磁極按順序編號，由式（2）得到任一磁極m在移動一定距離Δhm時對束流均勻性分布的影響，可以用式（3）表示，即磁極m的束流均勻性影響模型。

I0為初始束流均值，am、bm、wm、是與磁極m關(guān)聯(lián)的參數(shù)，由磁極結(jié)構(gòu)、束流狀態(tài)決定；ΔI為束流的影響。x為束剖面座標，hm表示調(diào)整前磁極m的磁極距，Δhm表示磁極m磁極距的變化量。

所有磁極同時調(diào)節(jié)對x點束流的影響為：

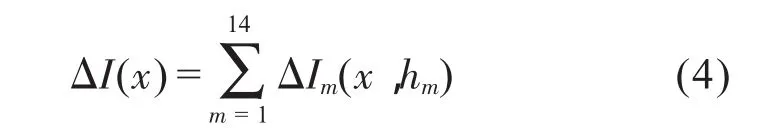
假設(shè)調(diào)節(jié)可調(diào)磁極組不會改變總束流大小，只改變束流水平均勻性分布，作為具有理想的束流均勻性情況下有：

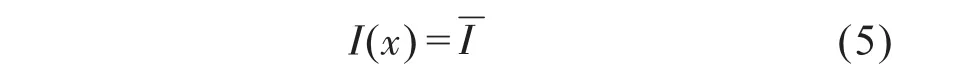
作為束流均勻性調(diào)節(jié)的目標，可以推導(dǎo)出均勻性調(diào)節(jié)模型：

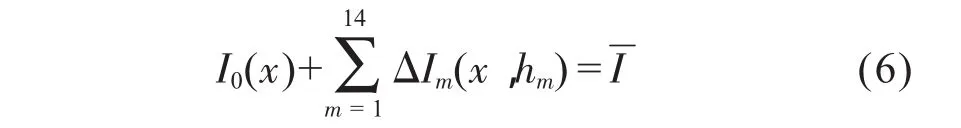
I0（x）為調(diào)節(jié)前束流分布值。

在實際束流均勻性檢測中，以靶臺為中心對稱取340 mm寬的束流數(shù)據(jù)計算束流均勻性，束流平均值按式（7）計算：

Ii為在所測點束流大小，j為數(shù)據(jù)點個數(shù)。在均勻性調(diào)節(jié)模型計算中，為了簡化計算量，束流均勻性分布數(shù)據(jù)細分為t個小區(qū)間，區(qū)間內(nèi)束流值為區(qū)間數(shù)據(jù)的平均值，忽略磁極之間的耦合影響，m個磁極對束流的影響在每個小區(qū)間內(nèi)疊加即得到束流均勻性調(diào)節(jié)模型：

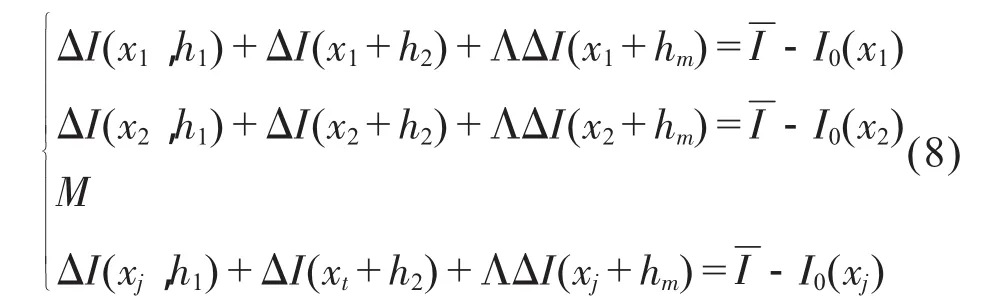
求解模型，其解就是可調(diào)磁極組的新極距值，通過多次迭代優(yōu)化調(diào)節(jié)，能將均勻性值逐次調(diào)低直至滿足要求。

模型ΔIm（x，hm）參數(shù)組（am、xm、wm）與離子注入機整機狀態(tài)相關(guān)，為保證模型的適用性，在每次進行均勻性調(diào)節(jié)之前，先通過束流均勻性測量系統(tǒng)得到束流均勻性分布初始數(shù)據(jù)，即I0（x），再給某個磁極極距一定的調(diào)節(jié)量，通過移動法拉第檢測調(diào)節(jié)后的束流均勻性分布數(shù)據(jù)，即I1（xn），通過比較所得兩次束剖面數(shù)據(jù)，求出所調(diào)磁極束流均勻性影響模型參數(shù)組值（am、xm、wm），然后通過內(nèi)/外插值法計算出其余磁極的束流均勻性影響模型參數(shù)［4］，獲得適時的束流均勻性調(diào)節(jié)模型。均勻性調(diào)節(jié)流程如圖4。

圖4　可調(diào)磁極組均勻性調(diào)節(jié)流程

3　試驗結(jié)果

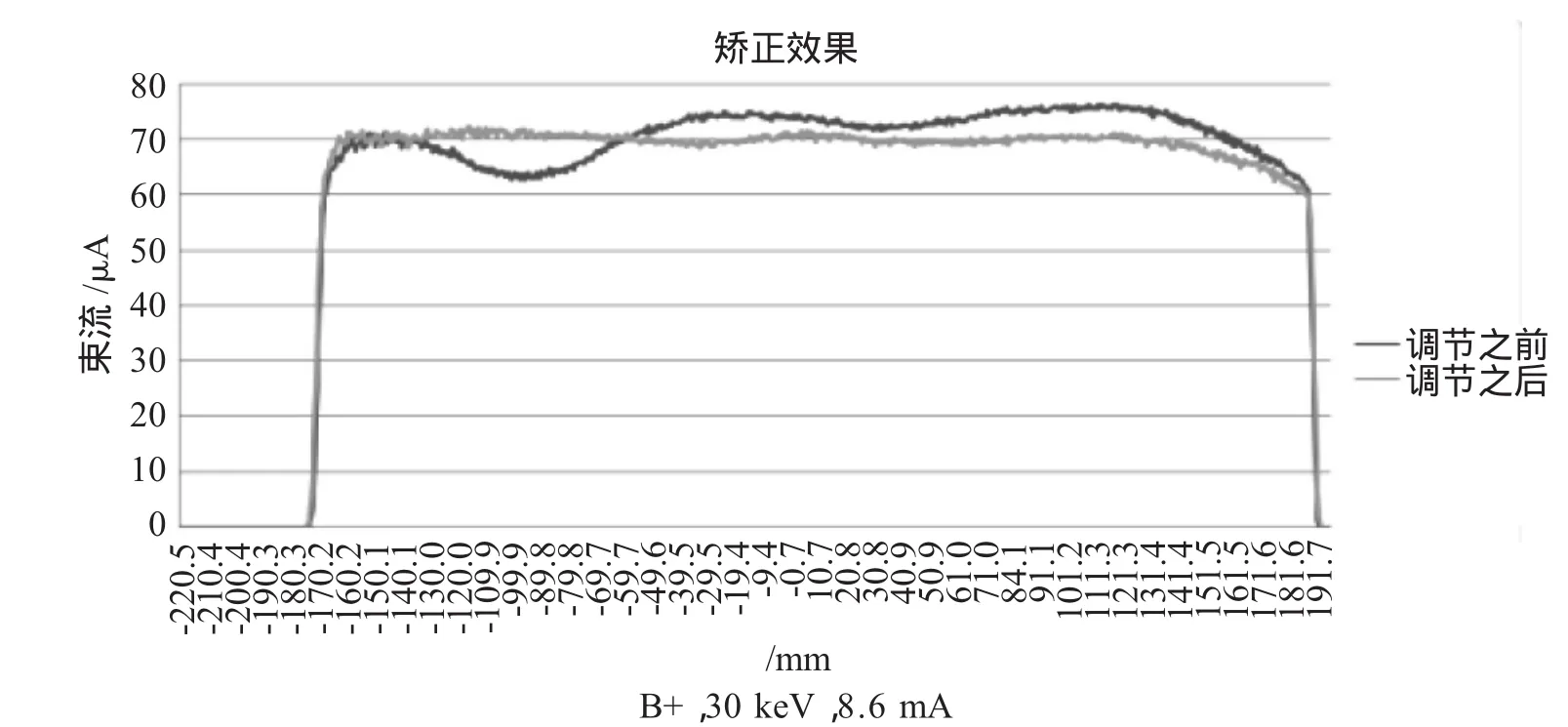
圖5　束流均勻性調(diào)節(jié)對比圖

用大束流寬帶束離子注入機對以上算法進行了驗證實驗，實驗條件：B+，束能量30 keV，總束流保持穩(wěn)定在2%以內(nèi)，均勻性調(diào)節(jié)模型求解用MATLBA實現(xiàn)。調(diào)節(jié)效果如圖5所示，調(diào)節(jié)之前束流均勻性分布為紅色曲線，均勻性指標為7.1%，經(jīng)過6次迭代調(diào)節(jié)之后達到綠色曲線，均勻性值為1.0%。注入300 mm硅片后，經(jīng)退火測方塊電阻值分布如圖6所示，均勻性為1.17%。

圖6　方塊電阻測試分布圖

4　結(jié)論

束流均勻性調(diào)節(jié)是寬帶束離子注入機的一項關(guān)鍵技術(shù)，在沒有可行的束流均勻性調(diào)節(jié)模型和算法的情況下，對線圈磁鐵組和可調(diào)磁極組中的每一個線圈的電流或磁極的位置進行一次調(diào)節(jié)，都需要通過移動法拉第對束流均勻性進行檢測，形成閉環(huán)，由于線圈磁鐵組和可調(diào)磁極組的調(diào)節(jié)單元數(shù)多，束流均勻性調(diào)節(jié)的工作效率將非常低，通過對單個線圈的電流調(diào)節(jié)和單個磁極的位置調(diào)節(jié)對束流均勻性的影響進行建模，形成線圈磁鐵組所有線圈電流參數(shù)和可調(diào)磁極組所有磁極位置參數(shù)整體調(diào)節(jié)對最終束流均勻性影響的預(yù)測算法，大幅提高束流均勻性調(diào)節(jié)的效率。本文研究了束流均勻性調(diào)節(jié)系統(tǒng)核心部件線圈磁鐵組與可調(diào)磁極組對束流均勻性影響的規(guī)律，建立了可調(diào)磁極組中單個磁極的束流均勻性影響模型及整機的束流均勻性調(diào)節(jié)算法模型，經(jīng)上機應(yīng)用測試，較好地實現(xiàn)了束流均勻性調(diào)節(jié)。

同時經(jīng)過上機實驗，發(fā)現(xiàn)基于以上調(diào)節(jié)模型的束流均勻性調(diào)節(jié)對初始束流均勻性狀態(tài)有較高的要求，需繼續(xù)研究提升調(diào)節(jié)效率和對束流狀態(tài)的適應(yīng)能力，調(diào)節(jié)模型和算法還有完善提升空間，如對模型參數(shù)進行自適應(yīng)的調(diào)整，改善模型在不同束流參數(shù)條件下與實際情況的匹配度，提升束流均勻性調(diào)節(jié)的運行效率。

［1］李薇薇，劉勝利，劉玉玲.微電子工藝基礎(chǔ)［M］.北京：化學(xué)工業(yè)出版社，2007.

［2］Huang S，Horng R，Tseng P.Study on hydrogen ion-imp anted characteristic of thin-film green resonant-cavity light-emitting diodes［J］.IEEE Photonics T-echnology Letters，2010，22（6）：404-406.

［3］王迪平，伍三忠，孫雪平.離子注入劑量的均勻性檢測和調(diào)節(jié)［J］.微納電子技術(shù)，2005，（10）：484-486.

［4］N.R.White，S.Satoh，E.W.Bwll，M.Sieradzki.Positive Control of Uniformity in Ribbon Beams for Implantation of Flat-Panel Displays［J］.International Conference on Ion ImplantationTechnology，1999，1（1）：354-357.

The Research of a Uniform Control Technique for High-Current Ribbon Beam Implanter

PENG Libo，ZHONG Xinhua，ZHANG Sai，ZHANG Jinxue

（The 48thResearch Institute of CETC，Changsha 410111，China）

The uniform control system is composed of coil group and adjustable pole groupin high-current ribbon beam implanter.By analysis for principle of adjustment，fitting the curve of effect of beam current uniform while a pole of pole group has been adjusted，a model for effect of uniform was established，further infer model for adjustment.For activity application，the reasonable control technique was designed，inside and outside interpolation based on actual beam is used to adjust the parameters of model for current uniform adjustment，flexibility of model is improved.Experiments show，by means of iteration algorithm，based on the model for beam uniform adjustment，the beam current uniformity can be adjusted，the measured dose un-uniformity of 300mm wafer is 1.17%.

Ribbon beam；Implanter；Uniform adjustment；Iterate algorithm

TN305.3

A

1004-4507（2016）10-0001-05

2016-09-17