彈性邊界條件下圓板橫向自由振動特性分析

石先杰, 李春麗, 蔣華兵, 康 甜

(中國工程物理研究院總體工程研究所 綿陽, 621900)

?

彈性邊界條件下圓板橫向自由振動特性分析

石先杰, 李春麗, 蔣華兵, 康 甜

(中國工程物理研究院總體工程研究所 綿陽, 621900)

采用譜幾何法(spectro-geometric method, 簡稱SGM)分析了彈性邊界條件下圓板橫向自由振動特性。首先,將圓板的振動位移容許函數描述為一種譜形式的改進三角級數，并采用沿邊界均勻分布的約束彈簧來模擬彈性邊界條件；然后，將未知級數展開系數看作廣義變量，應用瑞利-里茲法從能量的角度推導彈性邊界條件下圓板結構橫向自由振動系統特征矩陣方程;最后，設計搭建了相關實驗臺架，對圓板結構橫向自由振動模態參數進行測試。將文中方法計算結果與文獻解、有限元計算結果和實驗結果進行對比，驗證了譜幾何法求解圓板橫向自由振動問題的正確性和計算精度。

圓板； 橫向自由振動； 譜幾何法； 彈性邊界條件

引 言

圓板作為結構基礎部件，廣泛應用于航空航天、船舶工程、石化容器及鐵路交通等工程領域。板結構在外界激勵載荷作用下產生的劇烈振動常常會造成結構的疲勞破壞、機械故障、能量損耗，并降低結構的可靠性等性能。此外,結構還將通過振動向周圍環境輻射噪聲。因而，圓板結構的振動特性受到相關專家學者的廣泛關注。

幾十年來，學者們圍繞圓板結構振動問題做了大量的研究。有限元法[1]，能量法[2]和微分求積法等[3]各種解析或數值分析方法被相繼提出并用于求解圓板結構的動力學問題。Leissa[4]對板結構振動研究成果進行了較為全面系統的總結。Wu等[5]采用廣義微分求積法對徑向變厚度圓板自由振動問題開展了相關研究。Chen等[6]采用基于徑向基函數的無網格法求解了固支圓板和矩形板的自由振動問題。Yalcin等[7]采用微分變換法(differential transformation method，簡稱DTM)分析了簡支、固支和自由邊界條件下圓板的自由振動特性。Bauer等[8]研究了混合邊界條件(固支、簡支和自由邊界條件的任意組合)下圓板的固有振動頻率。

從上述研究情況來看，現有的研究方法大多限于特定的經典邊界條件，且為了適用于各種不同的邊界條件，大多需要不斷修改位移容許函數、相關的算法及相應的求解過程。而在實際工程應用中，圓板結構往往具有更加復雜的邊界條件，不僅包括固支、簡支和自由這三種經典邊界條件的任意組合，還包含彈性邊界約束條件[9]。此外，還存在局部約束的情況。

針對上述技術局限性和實際的工程需求，采用譜幾何法[10-11]建立彈性邊界條件下圓板結構橫向自由振動分析模型。通過將文中方法求解結果與相應文獻解和有限元法結果進行對比，驗證文中方法的正確性和有效性。隨后，搭建相關實驗臺架，開展圓板橫向自由振動實驗測量研究。

1 理論推導

1.1 圓板模型描述

為了克服圓板圓心處易出現的奇異現象，擬建立如圖1所示的環板模型，通過將內外半徑比設置為極小的數(b/a=10-5)來模擬圓板[12]。在板結構r=a的邊界上布置兩類連續的邊界約束彈簧，分別為線性位移彈簧(kt)和旋轉約束彈簧(Kr)。通過改變約束彈簧的剛度值大小來模擬不同邊界條件。當約束彈簧剛度值均設置為無窮大或零時，分別模擬固支和自由邊界條件。當線性位移彈簧剛度為無窮大，而旋轉約束彈簧剛度為零時，則為簡支邊界條件。

1.2 振動位移容許函數的級數表述

為了構建滿足彈性邊界條件的振動位移容許函數，并確保位移容許函數及其任意場點處空間坐標微分的連續性，采用譜幾何法將圓板結構的振動位移容許函數描述[13-14]為

(1)

其中

(2)

其中:Amn和Bmn分別為位移函數的未知級數展開系數。

此處，在標準傅里葉余弦級數基礎上，徑向(s)上引入四項正弦函數的目的在于消除振動位移容許函數及其相應空間導數在結構邊界上潛在的不連續性(或跳躍)現象，并去除Gibbs效應，以提高改進三角級數在整個求解域(包含邊界)內的收斂速度與求解精度。

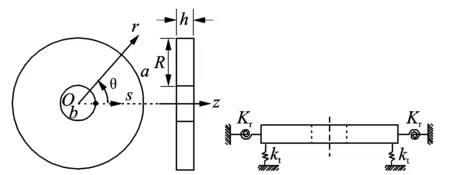
圖1 彈性邊界圓板橫向振動模型Fig.1 Transverse vibration model of circular plate with elastic boundary condition

為了闡明這點，假設一個函數f(x)在[0, π]區間上Cn-1連續，并且第n階導數絕對可積(第n階導數可能在某些點不存在)。三角級數的部分和表示為

(3)

從數學意義上可以證明級數展開系數滿足

(4)

如果系數am(m<0)可以表達為

(5)

更明確地預測收斂速度，式(5)可以描述為

(6)

這意味著

(7)

由此可以看出,收斂性在沒有額外代價的基礎上大幅提高了。值得指出的是，級數式(3)的收斂性可以通過設置合適的P值來控制。然而，對于一個給定邊值問題的解的光滑性在數學上是由在控制微分方程中出現的最高次微分來決定的。以文中研究的圓板橫向振動問題為例，其控制微分方程要求三階導數連續且四階導數在整個求解區域存在。因此，需要設定P=2來求取C3的強解，或者設定P=1來獲得弱解。由于當前級數的光滑性在整個求解區域是可控的，則未知級數展開系數可以通過強解形式或弱解形式來求解。

由于構建的位移場函數在整個求解域是足夠光滑的，則弱解和強解在數學意義上是等效的。文中將級數展開系數看作廣義坐標，并采用瑞利-里茲法來求解,這樣的解決方案更適合后續組合結構的振動建模。

1.3 求解方案

彈性圓板結構橫向自由振動的系統拉格朗日函數為

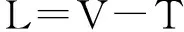
(8)

其中：V和T分別為結構系統的總勢能和總動能。

總勢能V包含板結構應變能和邊界約束彈簧儲存的彈性勢能兩部分，可以描述為

(9)

其中：D=Eh3/(12(1-μ2))為彎曲剛度；E為材料彈性模量；μ為泊松比；θ0和θ1分別代表邊界約束弧長的起始角度(0≤θ0≤θ1≤2π，通過調整θ0和θ1可以方便地求解任意局部邊界支撐下圓板振動問題)。

圓板結構橫向振動引起的總動能T為

(10)

其中：ρ為材料密度；ω為圓頻率。

將式(1)代入式(8)，采用瑞利-里茲法對位移場函數中的各個未知系數Amn和Bmn分別取極值，在實際計算過程中，改進三角級數進行有限截斷m=M，n=N，從而可以獲得關于未知級數展開系數的系統方程

(11)

其中：K和M分別為圓板結構的剛度矩陣和質量矩陣，其元素僅僅與板結構的材料特性、幾何參數和邊界條件相關，并直接決定了板結構系統的固有振動特性，即固有頻率及其對應的模態振型；X為一個包含所有未知級數展開系數的向量。

顯然，板結構的固有頻率及其特征向量可以通過式(11)而獲得。在求解框架中，通過將所得到的相應特征向量系數代入至振動位移場函數式(1)，即可獲得該階模態頻率所對應的物理模態振型。如需對某種外界載荷作用下的結構響應進行求解，僅需在系統的拉格朗日函數中增加外界載荷的做功項即可，最終在結構系統方程，式(11)右側出現外力激勵向量。一旦板結構的位移確定后，其他感興趣變量(如功率流、導納等)可以通過對位移函數直接進行相關數學操作而得到。

2 數值算例與實驗結果分析

2.1 數值算例分析

采用第1節的理論模型，對不同邊界條件下圓板結構的自由振動特性進行計算分析，將文中方法的計算結果與文獻解和有限元法結果進行比較，驗證文中方法和編寫程序的有效性與可靠性。在仿真模型中，圓板結構材料特性為：E=2.1×1011Pa，μ=0.3，ρ=7 850 kg/m3。由文中的物理模型描述可知，彈性邊界條件可以通過改變邊界約束彈簧剛度值而簡單獲得。對固支邊界條件，可以將所有約束彈簧剛度值設置為無窮大(在數值計算中，取為1013)即可，而振動位移場容許函數的級數截斷均取為M=N=12。

自由邊界條件代表了模型驗證的一種經典，但極具挑戰性的邊界條件。表1給出了自由邊界條件下圓板前6階最小無量綱頻率參數(Ω=ωa2(ρh/D)1/2。作為參考數據，文獻[15]和[16]的計算結果也列在表1中。從表中的數據對比分析可知，文中方法計算結果與文獻[15]和[16]方法求解結果吻合良好。

表1 自由邊界條件圓板前6階最小頻率參數Ω

Tab.1 The lowest six natural frequency parametersΩfor circular plate with free boundary condition

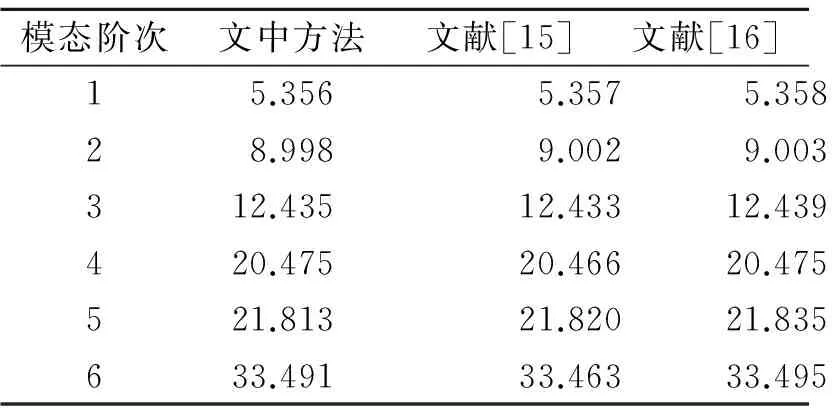
模態階次文中方法文獻[15]文獻[16]15.3565.3575.35828.9989.0029.003312.43512.43312.439420.47520.46620.475521.81321.82021.835633.49133.46333.495

表2列出了不同旋轉約束剛度Kr下簡支圓板前6階最小無量綱頻率參數Ω。Kr=0和1013時，邊界條件分別為簡支和固支。通過表2的對比分析可知，文中方法計算結果與文獻結果吻合程度較高。圖2繪制了Kr=105時圓板前4階模態振型情況。

表2 不同旋轉約束剛度Kr下簡支圓板前6階最小頻率參數Ω

Tab.2 The lowest six natural frequency parametersΩfor simply supported circular plate with variousKr

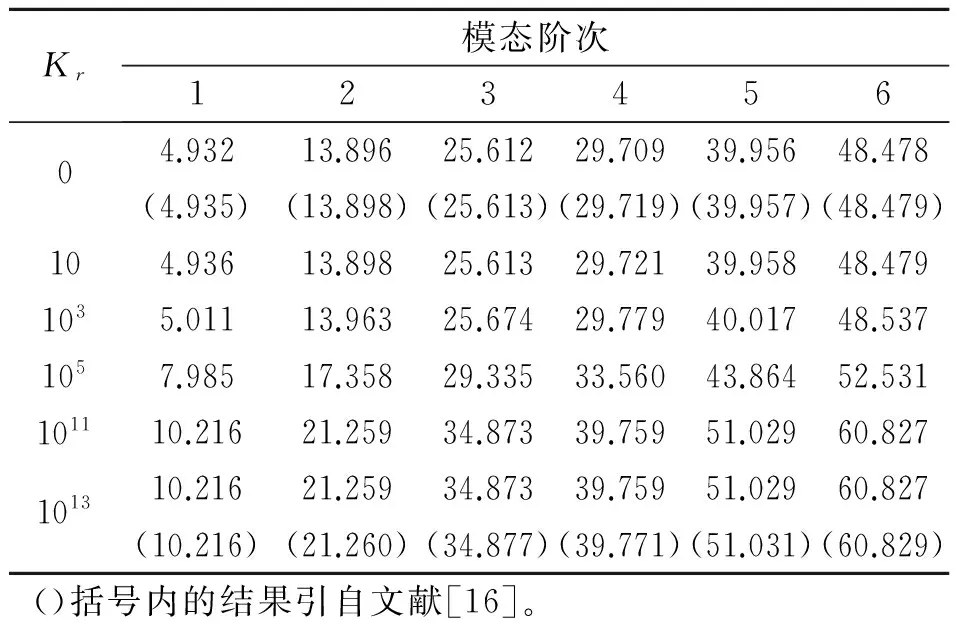
Kr模態階次12345604.93213.89625.61229.70939.95648.478(4.935)(13.898)(25.613)(29.719)(39.957)(48.479)104.93613.89825.61329.72139.95848.4791035.01113.96325.67429.77940.01748.5371057.98517.35829.33533.56043.86452.531101110.21621.25934.87339.75951.02960.827101310.21621.25934.87339.75951.02960.827(10.216)(21.260)(34.877)(39.771)(51.031)(60.829)()括號內的結果引自文獻[16]。

由第1節理論模型分析可知，文中構建的分析模型不僅可以適用于勻質邊界條件和彈性邊界，還可用于局部約束情況。因此，最后給出一個局部彈性邊界約束條件的算例，在r=a邊界存在局部勻質彈性約束，約束區間為(π/3, π)，而彈簧剛度值為Kr=kt=106。表3給出了局部彈性約束下圓板結構前6階固有頻率，ABAQUS的計算結果也列在表3中作為參考數據。

從表3的對比分析可以發現，兩組計算結果之間吻合程度良好，最大相對偏差僅為0.608%，滿足相關工程實際應用的需求。圖3為圓板結構前4階模態振型圖，同時也列出了ABAQUS分析獲得的模態振型圖，從而驗證了文中方法對局部彈性約束結構振型求解的準確性。

圖2 Kr=105時簡支圓板前4階模態振型Fig.2 The first fourth mode shapes for simply supported circular plate with Kr=105

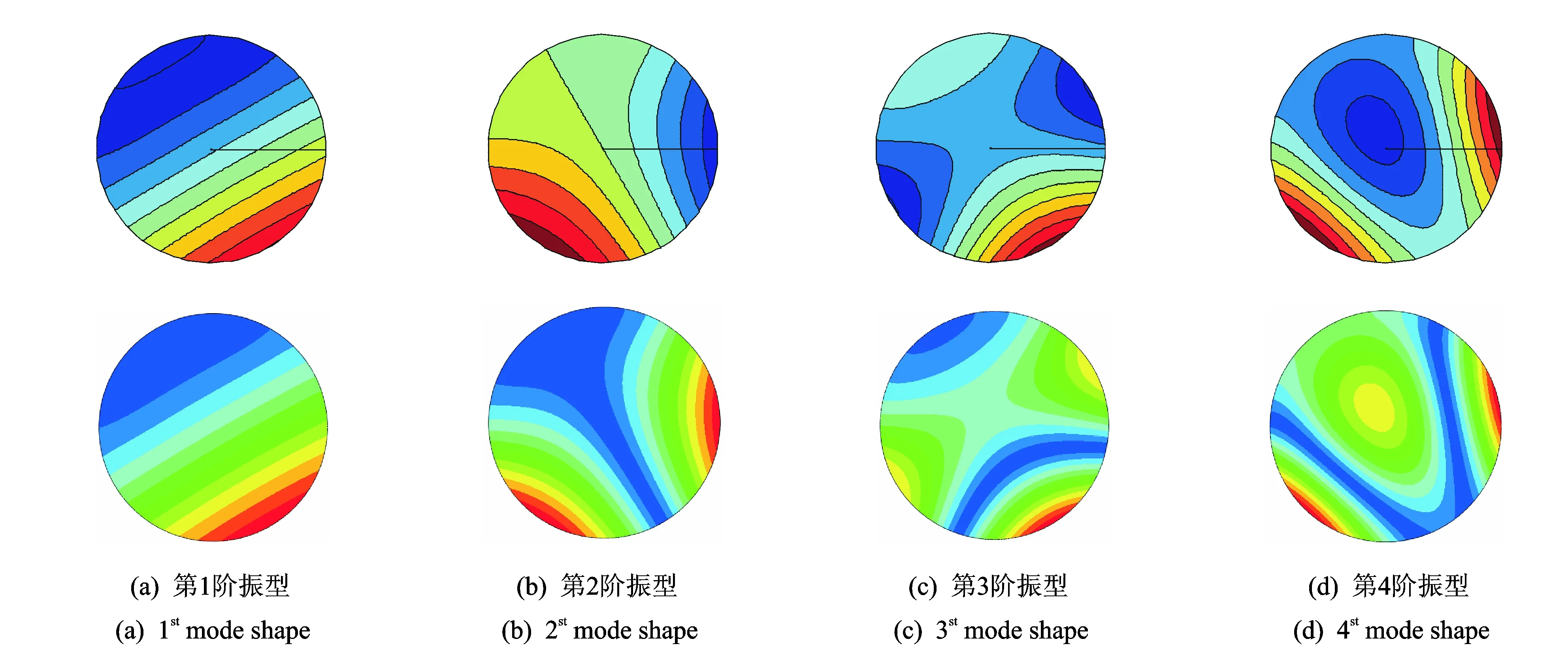
圖3 (π/3, π)弧彈性約束(Kr=kt=106)圓板前4階模態振型(第1行為文中方法結果，第2行為ABAQUS分析結果)Fig.3 The first fourth mode shapes of circular plate (with the arc (π/3,π) elastic restraint, Kr=kt=106): the first row is calculated by present method; the second row is calculated by ABAQUS

表3 (π/3, π)弧彈性支撐圓板前6階固有頻率(Kr=kt=106)

Tab.3 The first six natural frequencies for circular plate with the arc (π/3, π) elastic restraintKr=kt=106

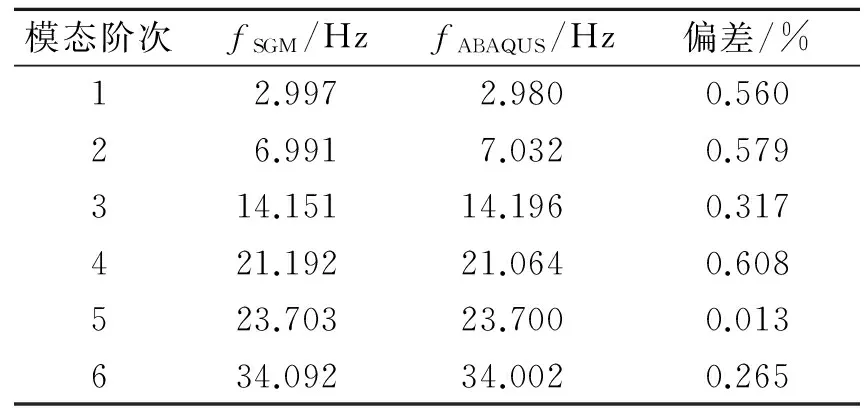
模態階次fSGM/HzfABAQUS/Hz偏差/%12.9972.9800.56026.9917.0320.579314.15114.1960.317421.19221.0640.608523.70323.7000.013634.09234.0020.265

2.2 圓板橫向自由振動實驗

圖4 圓板振動實驗裝置Fig.4 Vibration experiment setup of circular plate

為了從實驗角度對圓板橫向振動進行研究，搭建如圖4所示的實驗臺架。將半徑為126.95 mm、厚度為5.68 mm的圓板，通過邊緣位置的兩個細小吊孔，采用橡皮繩連接后吊掛于支架上來實現橫向振動的自由邊界條件。在實驗過程中，采用力錘在圓板表面沿垂直于圓板平面方向進行敲擊，以激起圓板橫向振動的彎曲波分量。圓板表面徑向和周向分別劃分為4和16等份，加上圓心處的1個測點，共計65個測點。依次在每一位置點處采用壓電式加速度傳感器DH131拾取力錘敲擊所激起的彎曲振動響應信號，力錘和加速度計的輸出信號則用多通道數據采集分析儀DH5922來采集，最后通過模態分析計算，獲得圓板結構的模態參數。模態測試結果如表4所示。模態振型分布測量與仿真結果部分對比情況如圖5所示。

表4 自由圓板前6固有頻率預測與實驗結果對比

Tab.4 Comparisons of the first six natural frequencies of circular plate with free boundary conditions between the predicted and test results

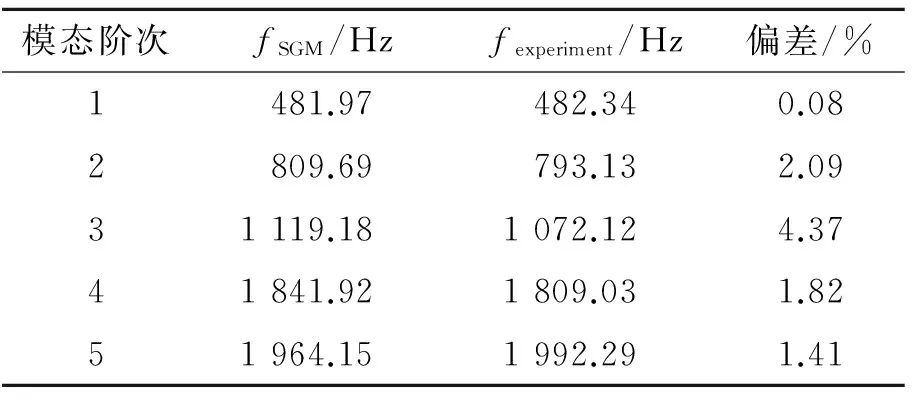
模態階次fSGM/Hzfexperiment/Hz偏差/%1481.97482.340.082809.69793.132.0931119.181072.124.3741841.921809.031.8251964.151992.291.41

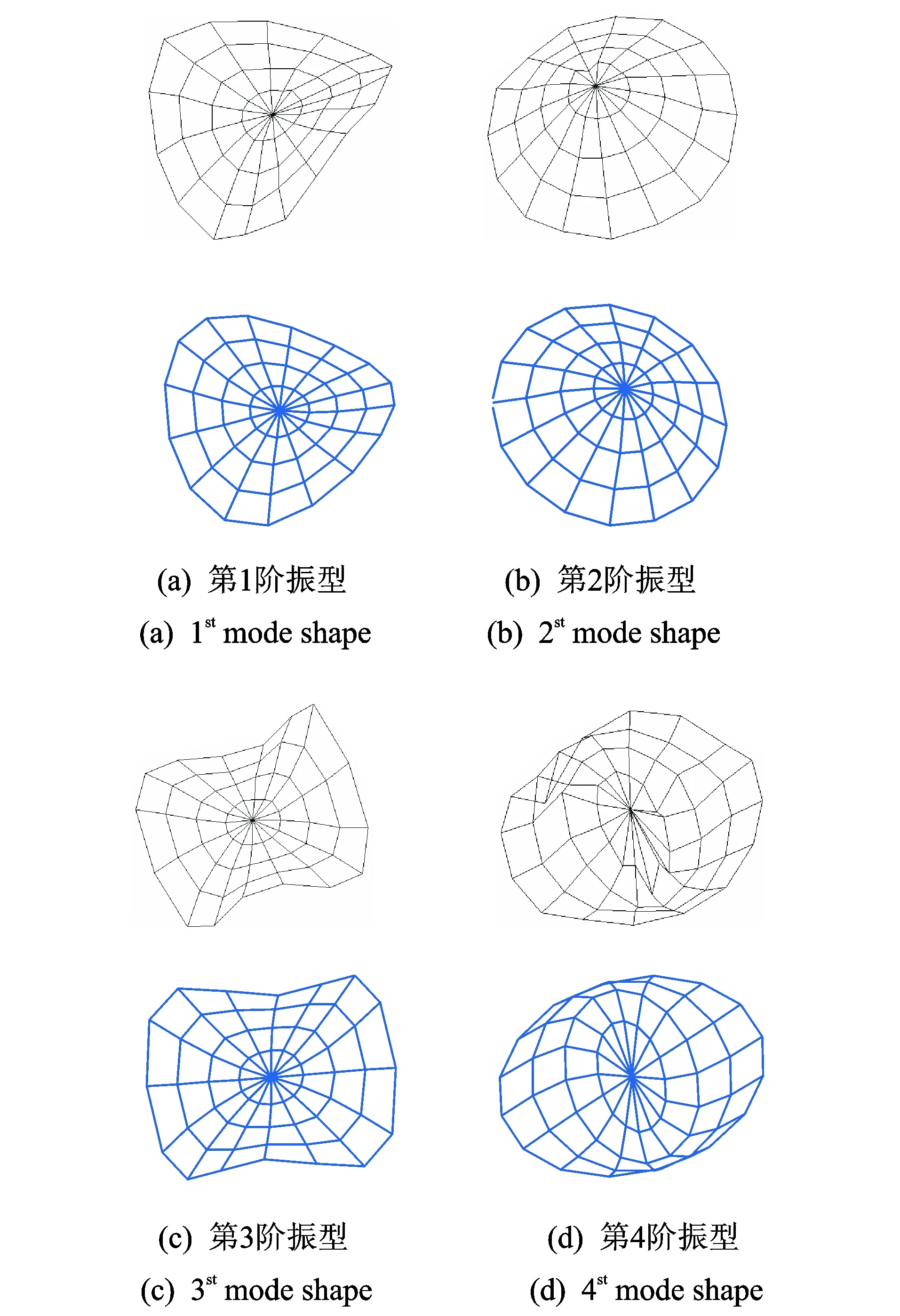
圖5 圓板橫向振動模態振型實驗與預測結果對比(第1行為測試結果，第2行為預測結果)Fig.5 Comparisons of vibration mode shapes of the circular plate between measured and predicted results (The first row is the measured results, the second row is obtained by the present method)

從表4的對比情況可知，兩種結果的吻合程度良好，再次驗證了文中構建的分析模型的正確性。從振型對比圖可以看出，除了個別測點的振動幅值過大或過小外，兩種振型的形狀和變化趨勢基本保持一致。由于在模態實驗過程中敲擊的輕重、偏離節點位置和敲擊過程中導致加速度傳感器的微幅移動均會使獲得的測量數據與實際振動情況之間存在著一定的數據偏差，且實驗結果沒有數值仿真結果那樣光滑均勻。

3 結 論

1) 彈性邊界支撐條件下圓板結構橫向自由振動位移場容許函數可表示為一種通用的改進三角級數形式。

2) 對級數進行相應截斷后，隨著級數截斷項數的增加，計算結果快速收斂，并且具有良好的數值穩定性。

3) 當改變邊界條件時，文中方法不需重新推導及編程，只需改變邊界約束彈簧剛度即可快速求解圓板橫向自由振動特性。

[1] Liu C F, Lee Y T. Finite element analysis of three-dimensional vibrations of thick circular and annular plates[J]. Journal of Sound and Vibration, 2000, 233(1): 63-80.

[2] Rajalingham C, Bhat R B. Axisymmetric vibration of circular plates and its analog in elliptical plates using characteristic orthogonal polynomials[J]. Journal of Sound and Vibration, 1993, 161(1): 109-118.

[3] Gupta U S, Lal R, Sharma S. Vibration analysis of non-homogeneous circular plate of nonlinear thickness vibration by differential quadrature method[J]. Journal of Sound and Vibration, 2006, 298(4): 892-906.

[4] Leissa A W. Vibration of plates[M]. Washington DC: US Government Printing Office, 1969: 1-32.

[5] Wu T Y, Liu G R. Free vibration analysis of circular plates with variable thickness by the generalized differential quadrature rule[J]. International Journal of Solids and Structures, 2001, 38(44): 7967-7980.

[6] Chen J T, Chen I L, Chen K H, et al. A meshless method for free vibration analysis of circular and rec-

tangular clamped plates using radial basis function[J]. Engineering Analysis with Boundary Elements, 2004, 28(5): 535-545.

[7] Yalcin H S, Arikoglu A, Ozkol I. Free vibration analysis of circular plates by differential transformation method[J]. Applied Mathematics and Computation, 2009, 212(2): 377-386.

[8] Bauer H F, Eidel W. Determination of the lower natural frequencies of circular plates with mixed boundary conditions[J]. Journal of Sound and Vibration, 2006, 292(3): 742-764.

[9] 史冬巖，孔令成，石先杰，等.彈性邊界板結構拓撲優化聲輻射[J].振動、測試與診斷，2014，34(1)：179-184，197.

Shi Dongyan, Kong Lingcheng, Shi Xianjie, et al. Topology optimization and sound radiation research of plates with elastic boundary[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(1): 179-184，197. (in Chinese)

[10]Li W L. Free vibrations of beams with general boundary conditions[J]. Journal of Sound and Vibration, 2000, 237(4): 709-725.

[11]Li W L, Zhang Xuefeng, Du Jingtao, et al. An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports[J]. Journal of Sound and Vibration, 2009, 321(1-2): 254-259.

[12]Mirtalaie S H, Hajabasi M A. Free vibration analysis of functionally graded thin annular sector plates using the differential quadrature method[J]. Proceedings of

the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2011, 225(3): 568-583.

[13]Shi Dongyan, Shi Xianjie, Li W L, et al. Free transverse vibrations of orthotropic thin rectangular plates with arbitrary elastic edge supports[J]. Journal of Vibroengineering, 2014, 16(1): 389-398.

[14]Shi Xianjie, Shi Dongyan, Li Wen L, et al. A unified method for free vibration analysis of circular, annular and sector plates with arbitrary boundary conditions[J]. Journal of Vibration and Control, 2016, 22(2): 442-456.

[15]Liu K M, Yang B. Three-dimensional elasticity solutions for free vibrations of circular plates: a polynomials-Ritz analysis[J]. Computer Methods in Applied Mechanics and Engineering, 1999, 175(1-2): 189-201.

[16]Zhou Zhenhuan, Wong K W, Xu Xinsheng, et al. Natural vibration of circular and annular thin plates by Hamiltonian approach[J]. Journal of Sound and Vibration, 2011, 330(5): 1005-1017.

10.16450/j.cnki.issn.1004-6801.2016.05.026

國家自然科學基金資助項目(51505445);中國工程物理研究院重點學科資助項目(計算固體力學)

2015-08-10；

2015-10-30

TH113; TB53

石先杰，男，1985年7月生，博士、工程師。主要研究方向為結構振動與噪聲控制等。曾發表《任意邊界條件下環扇形板面內振動特性分析》(《振動工程學報》2014年第27卷第1期)等論文。

E-mail: 411shixj@caep.cn