高階滑模控制及其研究現狀

孫靈芳 邢 宇 李 斌

(東北電力大學自動化工程學院，吉林 吉林 132012)

高階滑模控制及其研究現狀

孫靈芳 邢 宇 李 斌

(東北電力大學自動化工程學院，吉林 吉林 132012)

高階滑模控制器的研究已經成為解決抖振問題的熱點。總結了目前高階滑模控制研究的成果，歸納了它在國內外的應用，并探討了發展趨勢。

滑模控制 抖振 二階滑模控制 高階滑模控制

隨著科學技術的不斷發展，人們通過對不同物理系統進行研究，發現任何一個實際的物理系統都具有非線性特性。近幾十年來對非線性系統的研究推動了相關控制理論的發展，相平面理論、Lyapunov運動穩定性理論[1]都再次受到了極大的重視。然而，非線性特性仍然沒有統一通用的處理方法。總的來說，非線性控制理論還處于發展階段，有許多問題有待解決。

變結構控制方法是20世紀60年代由前蘇聯學者Utkin等提出的，它本質上是一種非線性控制[2]。這種控制策略原理是系統狀態有目的地不斷變化，迫使狀態在規定的狀態軌跡上運動。對于一個理想的滑模控制系統，系統狀態是可以嚴格地保持在滑模面上并且趨于穩定的。但實際情況是，由于控制規律的不連續性、開關時間或空間滯后性、系統延遲和慣性、測量中產生的誤差都會導致系統狀態并不能嚴格按照預定的狀態軌跡運動，這樣就會產生抖振。對于實際應用的滑模控制系統，抖振的存在是必然的，消除抖振也就相當于消除了滑模控制的優點。因此，消除抖振在滑模控制中是不可能實現的，只能在一定程度上削弱。

1 消除抖振的常用方法①

1.1 趨近律方法

高為炳教授提出了趨近律的方法來消除滑模變結構控制系統的抖振，通過調節趨近律中的參數，減小控制信號的抖振。但若參數調整不當，仍然會出現抖振現象。張合新等通過分析傳統趨近律存在的收斂速度慢、時間長及抖振等缺陷，提出了一種基于雙冪次趨近律的控制理論，該理論在遠離或接近滑動模態時均有較好的收斂性[3]。劉希等引入了趨近律變化速率的控制函數，設計了一種新的無抖振離散滑模變速趨近律算法，首次提出了通過設計趨近律變化速率來構造離散趨近律的思想[4]。

1.2邊界層的設計

邊界層設計的關鍵在于邊界層的厚度，該方法只能保證系統狀態收斂到邊界層內，這樣會降低系統的魯棒性。楊玲玲等對邊界層厚度用模糊控制的方法進行了調整，仿真結果表明該方法可以有效地抑制抖振，優化邊界層的厚度[5]。趙文杰和劉吉臻采用改進的邊界層法，在邊界層內采用非線性反饋，理論分析表明該方法可行[6]。

1.3濾波方法

濾波方法是指對通過濾波器的信號進行處理，使信號保持平滑狀態，進而減少抖振。Jin S H等提出了一種基于滑模自適應控制的離散時間濾波器，該濾波器可以得到更好的速度反饋[7]。此外，系統的控制器使用了反饋開關濾波器，使系統的非穩定參數在變化范圍內，具有調整信號誤差和過濾信號參數的功能[8]。

1.4動態滑模方法

動態滑模方法是指將傳統切換函數通過微分環節構成新的切換函數，以達到削弱抖振的目的。李春華等利用自適應技術和反演法設計了動態滑模控制器，可以有效地削弱抖振[9]。Bartolini G等通過設計切換函數的二階導數，實現了不確定性系統的無抖振滑模控制，并將該方法引入到多輸入多輸出系統中[10,11]。

1.5其他方法

除了上述4種普通方法以外，對于抑制抖振還有降低切換增益方法、干擾器觀測方法、模糊方法、神經網絡方法、扇形區域方法、遺傳優化方法及H∞方法[12～18]等，上述各種方法適用于不同情況下的控制器設計，要依據具體需求進行選擇組合[19]。

2 高階滑模控制方法

近年來，高階滑模控制成為研究滑模變結構控制學者們關注的熱點。高階滑模是傳統一階滑模的擴展，由Fridman L和Levant A提出的高階滑模控制方法通過將不連續的控制變量作用到滑模變量的高階導數上，不但保留了傳統滑模控制的主要優點、提高了控制精度，還有效地抑制了抖振[20]。

2.1滑動階的定義

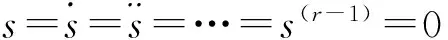
二階滑模是最早出現的高階滑模，因為控制器簡單并且需要的信息量較少，二階滑模的應用也是最廣泛的。下面簡單介紹幾種常見的二階滑模算法[23～26]。

2.2問題描述

考慮如下非線性系統：

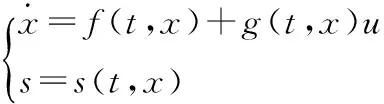
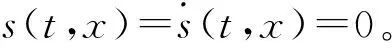
依據相對階的定義，對滑模變量做兩種情況的考慮：

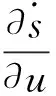
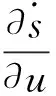
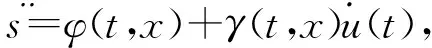
2.3螺旋算法

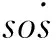
當系統相對階為1時，算法形式如下：

需滿足的條件為：

KmλM-C0>KMλm+C0

當系統相對階為2時，算法形式如下：

2.4超螺旋算法

超螺旋算法與其他二階滑模算法相比存在的特殊之處為只需要s的信息，而且當控制系統的相對階為1時，利用超螺旋算法可以避免抖振。

超螺旋算法的控制器由兩部分組成，其中一部分為對時間不連續的導數項，另一部分為滑模變量s的連續函數，控制器的具體形式如下：

u=u1(t)+u2(t)

保證算法在有限時間收斂的條件為：

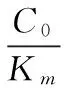
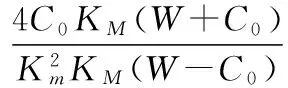
0.0<ρ≤0.5

2.5給定收斂率算法

其中，g(s)除s=0外均光滑，λM是一個正常數。

當相對階為2時，控制器為：

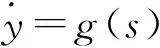
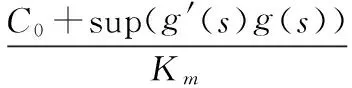
其中sup表示上確界，收斂時間與函數g有關。

以上給出了幾種常見的二階滑模控制器。此外還有由Bartolini G等提出的次優算法[27,28]，該算法由時間最優控制演化而來。李雪冰等提出了一種新的二階滑模算法，算法采用加冪積分技術和嵌套飽和技術，解決了系統不確定性由非負函數限定的問題[29]。Madhulika D和Chitralekha M給出了一種最優二階滑模控制器用來穩定不確定非線性系統[30]。

3 任意階滑模控制器

二階滑模控制是高階滑模控制的一個分支，適用于系統相對階不大于2的情況。下面簡要介紹兩種當系統的相對階為r時，對于單輸入單輸出系統的高階滑模控制器的設計[31～34]。

3.1任意階“嵌套”高階滑模控制器

任意階滑模控制器經證明可以在有限時間內收斂，r階控制器的通用遞歸程序為：

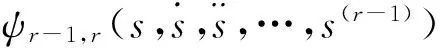
i=1,2,…,r-1

N1,r=|s|(r-1)/r

ψ0,r=sign(s)

ψi,r=sign(s(i)+βiNi,rψi-1,r)

其中α、β和p是需調整的控制器參數，當r≤4時，若取適當的參數可以得到如下的“嵌套”控制器結構：

r=1u=-αsign(s)

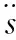
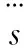
當相對階k小于滑模控制階數r-1時，控制變量對于k-r-1的時間導數是連續的，這樣就可以有效地消除抖振。

3.2任意階“準連續”高階滑模控制器

Levant A又提出了一種被稱為“quasi-continuous”控制器的高階滑模控制器，可以使滑動模態在有限時間內達到穩定，該“準連續”高階滑模控制器形式如下：

φ0,r=s

N0,r=|s|

ψ0,r=φ0,r/N0,r=sign(s)

ψi,r=φi,r/Ni,r

當r≤4時，選取適當的參數β可以得到如下控制器的結構：

r=1u=-αsign(s)

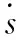
r=4u=-αφ3,4/N3,4

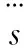
通過以上兩種高階滑模控制器的遞推形式可以看出，控制器參數β的選取結果是相同的，通過調整參數可以得到需要的收斂率。Levant A認為第二種“quasi-continuous”控制器的控制效果優于其他類型高階滑模控制器的效果，不但可以抑制抖振，而且參數調整簡便。

除了以上兩種經典形式的高階滑模控制器，目前國內外學者們經過不斷的學習和改善，提出了許多新型的高階滑模控制器。陳杰等提出了一種新的高階滑模控制器，主要針對一類不確定非線性單輸入單輸出系統，利用積分滑模控制理論和有限時間穩定理論，確保系統在最初時刻就具有抗干擾能力[35]。范金鎖等通過引入虛擬控制項增加系統相對階，進而對高階滑模控制器進行改進，與原控制器相比控制更平滑[36]。

4 高階滑模控制研究現狀

高階滑模控制自提出以來，就得到了國內外學者的廣泛關注并且取得了飛速的發展。與此同時，高階滑模控制存在的問題也日益凸顯。

目前高階滑模控制主要應用于不確定性非線性系統，然而在實際工程應用中，系統的不確定性邊界是很難獲得的。為了能使高階滑模控制器更容易面向實際工程應用，目前研究趨勢主要是將高階滑模控制器與其他控制方法相結合，其中最常見的就是將高階滑模控制器與自適應控制相結合。Vadim I U和Alex S P提出了一種自適應反饋超螺旋算法，將一個低通濾波器作為等效控制，這種方法為滑模控制提供了一種可以使抖振最小化的控制增益，并且利用數值的例子證明了這種方法的有效性[37]。Yuri S等給出了一種新型的超螺旋自適應律并且應用在電動氣動制動器上，自適應算法的主要優點是可以得到非高估的控制增益，通過證明可以得到閉環控制系統在有限時間內收斂和Lyapunov穩定性，實物試驗得到了良好的效果[38]。

高階滑模控制器為普通的不確定非線性單輸入單輸出系統提供了有效解決方案，但是在工程實際中，多輸入多輸出系統仍然是研究的主要對象。在傳統滑模控制中，有學者通過解耦將多輸入多輸出系統分解成多個多輸入單輸出系統并實現了控制[39,40]。Liu X J和Han Y Z針對一類仿射多輸入多輸出不確定非線性系統，提出了一種新的高階滑模控制方法，將多輸入多輸出系統高階滑模控制問題轉化為多變量系統的有限時間收斂問題，削弱了控制量的抖振，在氣墊船軌跡跟蹤方面的試驗驗證了方法的有效性[41]。Khan M K和Sarah K S提出了一種新的二階滑模控制算法，主要應用于一類多輸入多輸出系統，該算法產生一個動態控制且不需要滑動變量的導數，因此不需要進行觀測器和峰值檢測電路的設計[42]。近幾年，對于不確定非線性多輸入多輸出系統的高階滑模控制器的研究已有理論上的補充，但是這些仍然不能滿足實際工業對控制的需求，這也說明了這類控制器的研究有非常大的發展空間。

除了以上兩點控制器設計存在的問題以外，不確定非線性高階滑模控制器應用于實際工程問題時仍然得不到理想的控制效果，這其中的原因來自于在實際工程中系統很難獲得精確的非線性模型。若沒有精確的非線性模型，此時設計的控制器也就不再適用，甚至會導致控制系統癱瘓，造成不必要的損失。因此，在對高階滑模控制器進行研究的同時，也要保證非線性模型精確，不但符合理論而且符合實際，這樣才能使控制器發揮應有的效果。

5 結束語

綜上所述，高階滑模控制器的研究還處于初級階段，應在現有的理論成果基礎上進一步擴充和發展。研究方向應根據高階滑模控制目前存在的問題和不足，在設計上提出有效可行的解決方案，或是針對具體問題進行分析，對于不同的系統控制中存在的缺陷定點改善，使高階滑模控制器具有較好的實際應用效果，不但可以抑制抖振，而且可以增強系統的魯棒性、提高系統可控性、減少超調量、使系統性能進一步提升。高階滑模控制器的研究將為機器人、電動機、飛行器及運載火箭等一類復雜非線性系統控制提供有利的控制方法，具有十分重要的發展意義。

[1] Hassan K K.Nonlinear Systems[M].Hongkong:Pearson Education Asia Ltd,2002:398～404.

[2] Liu J K,Sun F C.Research and Development on Theory and Algorithms of Sliding Mode Control[J].Control Theory and Applications,2007,24(3):407～418.

[3] 張合新,范金鎖,孟飛,等.一種新型滑模控制雙冪次趨近律[J].控制與決策,2013,28(2):289～293.

[4] 劉希,孫秀霞,董文瀚,等.一種新的約束變速趨近律離散滑模控制方法[J].自動化學報,2013,39(9):1552～1557.

[5] 楊玲玲,章云,陳曉龍.一類不確定非線性系統的模糊邊界層滑模控制[J].系統仿真學報,2009,21(22):7262～7265.

[6] 趙文杰,劉吉臻.一種改進的邊界層滑模控制方法[J].系統仿真學報,2005,17(1):156～158，180.

[7] Jin S H,Ryo K,Motoji Y.Improving Velocity Feedback for Position Control by Using a Discrete-time Sliding Mode Filtering with Adaptive Windowing[J].Advanced Robotics，2014,28(14):943～953.

[8] Matviichuk K S.Stability in Sliding Mode of Nonstationary Automatic-control Systems of Variable Structure with Switched Filters[J].International Applied Mechanics,2006,42(10):1179～1194.

[9] 李春華,孫約,羅琦.非線性系統的反演自適應動態滑模控制[J].計算機工程與設計,2009,30(1):185～187.

[10] Bartolini G,Punta E.Chattering Elimination with Second-order Sliding Mode Robust to Coulomb Friction[J].Journal of Dynamic Systems Measurement and Control,2000,122(4):679～686.

[11] Bartolini G,Pisano A,Punta E.A Survey of Applications of Second-order Sliding Mode Control to Mechanical Systems[J].International Journal of Control,2003,76(9-10):875～892.

[12] Zhang C, Chen Z J, Wei C.Sliding Mode Disturbance Observer-based Backstepping Control for a Transport Aircraft[J].Science China Information Sciences,2014,57(5):1～16.

[13] Mahmoodabadi M J,Taherkhorsandi M,Talebipour M,et al.Adaptive Robust PID Control Subject to Supervisory Decoupled Sliding Mode Control Based upon Genetic Algorithm Optimization[J].Transactions of the Institute of Measurement and Control,2015,37(4):505～514.

[14] Nagarale R M,Patre B M.Composite Fuzzy Sliding Mode Control of Nonlinear Singularly Perturbed Systems[J].ISA Transactions,2014,53(3):679～689.

[15] Fei J T,Ding H F.Adaptive Sliding Mode Control of Dynamic System Using RBF Neural Network[J].Nonlinear Dynamics,2012,70(2):1563～1573.

[16] 牛雪梅,高國琴,鮑智達,等.基于加權積分增益的溫室移動機器人滑模控制研究[J].控制工程,2013,20(6):1207～1211.

[17] 王健安,劉賀平.具有未知扇區非線性輸入混沌系統的自適應滑模投影同步[J].北京科技大學學報,2010,32(6):807～811.

[18] Zhang B L,Ma L,Han Q L.Sliding ModeH∞Control for Offshore Steel Jacket Platforms Subject to Nonlinear Self-excited Wave Force and External Disturbance[J].Nonlinear Analysis:Real World Applications,2013,14(1):163～178.

[19] 張曉宇,蘇宏業.滑模變結構控制理論進展綜述[J].化工自動化及儀表,2006,33(2):1～8.

[20] Fridman L,Levant A.Higher Order Sliding Modes as a Natural Phenomenon in Control Theory[J].Robust Control via Variable Structure and Lyapunov Techniques,1996,217:107～133.

[21] Fridman L,Levant A.Robust Control via Variable Structure and Lyapunov Techniques [M].London：Springer Berlin Heidelberg,1996:107～133.

[22] Filippov A F.Differential Equation with Discontinuous Right-hand Side[J].Matematicheskii Sbornik,1960,93(1):99～128.

[23] Levant A.Principles of 2-Sliding Mode Design[J].Automatica,2007,43(4):576～586.

[24] Levant A.Finite-time Stabilization of Uncertain SISO Systems[C].Proceeding of the 46th IEEE International Conference on Decision and Control.New Orleans,USA:IEEE,2007:1728～1733.

[25] Levant A.Construction Principles of Output-feedback 2-Sliding Mode Design[C].Proceedings of the 41st IEEE Conference on Decision and Control.Las Vegas，USA:IEEE,2002:317～322.

[26] Levant A.Higher-order Sliding Modes,Differentiation and Output-feedback Control[J].International Journal of Control,2003,76(9-10):924～941.

[27] Bartolini G,Ferrara A,Usai E.Output Tracking Control of Uncertain Nonlinear Second-Order Systems[J].Automatica,1997,33(12):2203～2212.

[28] Bartolini G,Ferrara A,Usai E. Chattering Avoidance by Second-Order Sliding Mode Control[J].IEEE Transactions on Automatic Control,1998,43(2):241～246.

[29] 李雪冰,馬莉,丁世宏.一類新的二階滑模控制方法及其在倒立擺控制中的應用[J].自動化學報,2015,41(1):193～202.

[30] Madhulika D,Chitralekha M.Optimal Second Order Sliding Mode Control for Nonlinear Uncertain Systems[J].ISA Transactions,2014,53(4):1191～1198.

[31] Levant A.Homogeneous High-Order Sliding Modes[C].Proceedings of the 17th World Congress the International Federation of Automatic Control.Seoul,Korea:IFAC，2008:3799～3810.

[32] Levant A.Homogeneity Approach to High-Order Sliding Mode Design[J].Automatica,2005,41(5):823～830.

[33] Levant A.Quasi-continuous High-order Sliding-mode Controllers[C].Proceedings of the 42nd IEEE Conference on Decision and Control.Hawaii,USA：IEEE，2003:4605～4610.

[34] Levant A.Homogeneous Quasi-continuous Sliding Mode Control[M].Berlin：Springer,2006:143～168.

[35] 陳杰,李志平,張國柱.不確定非線性系統的高階滑模控制器設計[J].控制理論與應用,2010,27(5):563～569.

[36] 范金鎖,張合新,王桂明,等.一種高階滑模控制算法的改進及應用[J].控制與決策,2011,26(9):1436～1440.

[37] Vadim I U,Alex S P.Adaptive Sliding Mode Control with Application to Super-twist Algorithm:Equivalent Control Method[J].Automatica,2013,49(1):39～47.

[38] Yuri S,Mohammed T,Franck P.A Novel Adaptive-gain Supertwisting Sliding Mode Controller:Methodology and Application[J].Automatica,2012,48(5):759～769.

[39] 戴永彬,楊衛東,王少福,等.基于滑模的多變量廣義預測解耦控制[J].化工自動化及儀表,2009,36(5):18～20，39.

[40] 戴永彬,白延玉,蔡艷慧.基于單值預測的遞推滑模解耦控制[J].化工自動化及儀表,2010,37(10):26～28.

[41] Liu X J,Han Y Z.Finite Time Control for MIMO Nonlinear System Based on Higher-order Sliding Mode[J].ISA Transactions,2014,53(6):1838～1846.

[42] Khan M K,Sarah K S.Robust MIMO Water Level Control in Interconnected Twin-tanks Using Second Order Sliding Mode Control[J].Control Engineering Practice,2006,14(4):375～386.

Higher-orderSlidingModeControlandResearchStatus

SUN Ling-fang, XING Yu, LI Bin

(SchoolofAutomationEngineering,NortheastDianliUniversity,Jilin132012,China)

High-order sliding mode controller can eradicate chattering problems. The investigation results of the higher-order sliding mode control were summarized, including its application at home and abroad and later development trend.

sliding mode control, chattering, second-order sliding mode control, high-order sliding mode control

2015-06-19(修改稿)

TP13

A

1000-3932(2016)04-0335-06