基于系統生物學的干擾素-γ建模的信號轉導模式分析

齊云峰,孫添添,常紅玲

(吉林師范大學生命科學學院，吉林四平 136000)

?

基于系統生物學的干擾素-γ建模的信號轉導模式分析

齊云峰,孫添添,常紅玲

(吉林師范大學生命科學學院，吉林四平 136000)

干擾素-γ是細胞因子超家族中干擾素家族的成員,具有抗微生物感染及免疫調節等多種生物學功能。系統生物學主要采用系統的方法研究生物體不同層次的建模與仿真、各種信號轉導途徑、基因調控網絡等。本文采用系統生物學建模工具COPASI對干擾素-γ的信號轉導進行模擬，并應用統計學方法進行檢驗，通過模擬分別改變干擾素-γ受體(IFNR)和磷酸酶PP2的初始濃度,研究二者濃度改變對細胞核內STAT同源二聚體濃度變化的影響。進而研究它們在干擾素-γ信號轉導過程中的協同作用。

系統生物學；干擾素-γ；信號轉導

系統生物學是一門以系統的觀點、運用各種先進的生物學手段從整體的角度分析和研究生命機體復雜特性的學科。它通過研究某生物系統各個不同部分之間的相互關系和相互作用，建立整個系統的可理解模型[1-2]。系統生物學主要在生物個體、器官、組織和細胞等基礎上，對其建模、生化代謝途徑、信號轉導途徑、基因調控網絡以及疾病機制等進行研究[3-4]。

干擾素-γ的信號轉導主要通過JAK/STAT信號轉導通路實現，受多種因子調節[5]，主要有PP2、IRNR、STAT等。STAT含有SH2和SH3結構域，可與特定的含磷酸化酪氨酸的肽段結合。JAK/STAT通路信號轉導的最終實現依賴于STAT同源二聚體進入細胞核內并行使其轉錄激活功能。STAT同源二聚體是干擾素-γ的信號轉導通路的直接轉錄因子，對其轉導過程起著至關重要的作用[6]。

隨著系統生物學的發展，研究者對IFN-γ的信號轉導的研究也更加深入，構建了更多的信號轉導模型。在2003年，Yamada等人公布了首個描述IFN-γ/JAK/STAT1信號轉導的數學模型[7]。Zi等人在2005年提出一種全新的方法——敏感性分析方法[8]。2010年，Rateitschak等人構建了另外一個IFN-γ/JAK/STAT1信號轉導模型[9]。

1 材料與方法

1.1 統計學方法

統計學方法是指將有關數據進行收集、整理、分析，通過對其所反映的問題總結得出結論的方法[10]。本文中使用SPSS軟件對實驗數據進行Pearson相關性或多元線性回歸分析，并計算其統計顯著性水平。相關系數用r表示，r值在1與-1之間，小于0表示負相關，大于0表示正相關[11]。

1.2 建模工具SBML簡介

隨著系統生物學建模工具不斷增多，在科學研究過程中可能需要幾種不同的建模工具，而不同建模工具構建的模型存在不兼容性，這成為系統生物學建模過程中一個亟待解決的問題。2003年，Hucka等人在可擴展標示語言(XML)的基礎上創建了SBML[12-13]。

1.3 建模工具COPASI介紹

本文主要使用的建模工具是COPASI，它是在GEPASI的基礎上衍生而來的[14]。COPASI工具是一個開源的軟件應用程序，能夠用來構建和分析系統生物學模型[15]。本文研究的是不同時間的干擾素-γ信號轉導過程中的直接轉錄因子STAT同源二聚體的濃度與干擾素-γ的R受體以及共享磷酸酶PP2之間變化關系的模型，需要通過Tasks模塊下的Time course功能區域進行模型構建，然后將數據輸出，根據數據構建STAT同源二聚體濃度與R受體濃度、STAT同源二聚體濃度與共享磷酸酶PP2濃度關系的模型圖。

2 結果與分析

本章中進行的模擬分析均以0.1nM的干擾素-γ作為輸入，模型的基準濃度是IFNR和PP2分別為12nM和60nM，我們通過擾動IFNR和PP2的初始濃度，進行12小時內干擾素-γ信號轉導的數學模擬。

2.1 不同受體濃度的干擾素-γ信號轉導調控模式分析

通過擾動IFNR的初始濃度，研究IFNR的濃度改變對細胞核中STAT1的同源二聚體和STAT3的同源二聚體濃度變化的影響。

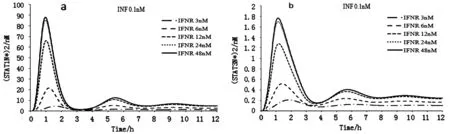
a.不同IFNR初始濃度下(STAT1N*)2濃度時序性變化模式 b.不同IFNR初始濃度下(STAT3N*)2濃度時序性變化模式圖1 不同濃度IFNR與(STAT1N*)2及(STAT3N*)2濃度時序變化

如圖1a和1b所示，可知細胞核內STAT1的同源二聚體在1.5小時左右出現最大。當IFNR的濃度升高至24nM和48nM時，隨著IFNR的濃度的升高(STAT1N*)2濃度已變化不大；圖1a(STAT1N*)2大約在9小時后基本趨于穩定狀態，(STAT1N*)2穩定濃度變化趨勢與峰值基本一致，濃度差異減小。圖1b大約在8小時后基本趨于穩定狀態，穩態濃度變化趨勢與峰值相同，濃度差異減小。

運用SPSS19軟件，對(STAT1N*)2和(STAT3N*)2與IFNR的相關性進行檢驗，得出(STAT1N*)2和IFNR之間的標準相關系數為0.819，P值為0.09，(STAT3N*)2和IFNR之間的標準相關系數為0.826，P值為0.085。結果表明，(STAT1N*)2和(STAT3N*)2的濃度與IFNR的濃度變化呈正相關，且為不顯著相關。由此推測，干擾素-γ信號轉導過程受IFNR的濃度的影響，適當地增加IFNR的濃度可以促進干擾素-γ的信號轉導。

2.2 不同濃度磷酸酶PP2的干擾素-γ信號轉導調控模式分析

通過擾動PP2的初始濃度，研究改變PP2的濃度，細胞核中STAT1的同源二聚體和STAT3的同源二聚體濃度在12小時內隨時間的變化。

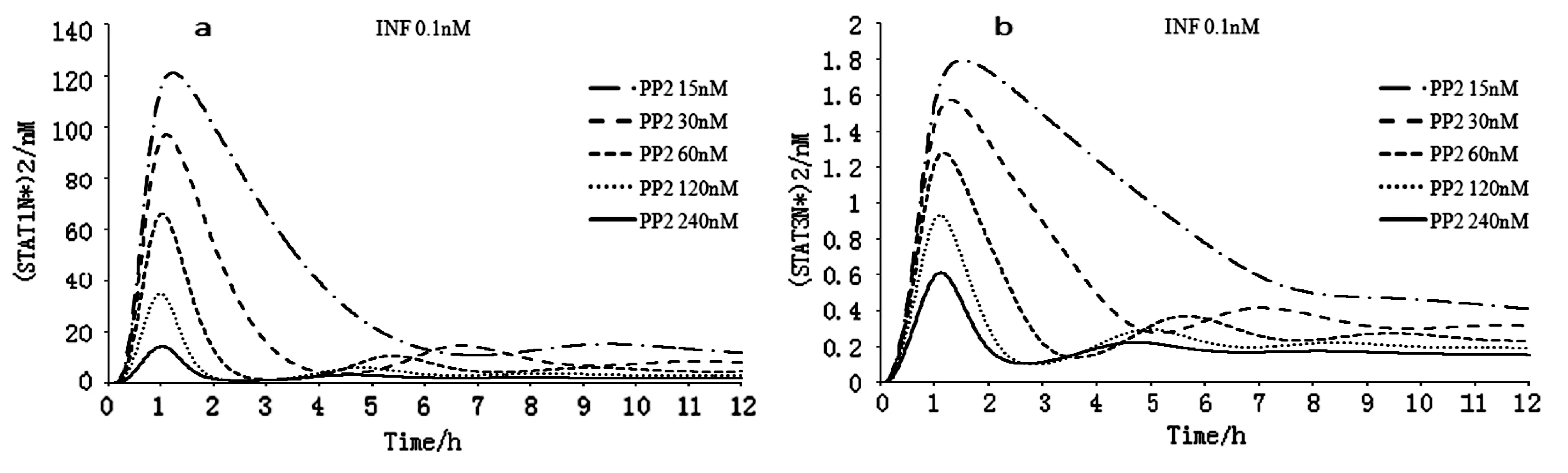
a.不同PP2初始濃度下(STAT1N*)2濃度時序性變化模式 b.不同PP2初始濃度下(STAT3N*)2濃度時序性變化模式圖2 不同濃度PP2與(STAT1N*)2及(STAT3N*)2濃度時序變化

如圖2a和2b所示，細胞核內STAT1的同源二聚體在1小時左右達到峰值。圖2a可看出(STAT1N*)2在大約在11小時后基本趨于穩定狀態，穩態濃度變化趨勢與峰值相同，濃度差異減小。圖2b(STAT3N*)2在1小時后逐漸恢復正常水平，大約在11小時后基本趨于穩定狀態，穩態濃度變化趨勢與峰值相同，濃度差異減小。

運用統計學方法對(STAT1N*)2和(STAT3N*)2與PP2的相關性進行檢驗，得出(STAT1N*)2和PP2之間的標準回歸系數為-0.929，P值為0.013，(STAT3N*)2和PP2之間的標準回歸系數為-0.951，P值為0.013。結果表明，(STAT1N*)2和(STAT3N*)2的濃度與PP2的濃度變化呈負相關，且顯著相關。這與Yamada等人的實驗結果相符[7]。由此推測，干擾素-γ信號轉導過程受PP2的濃度的影響，增加PP2的濃度可以抑制干擾素-γ的信號轉導。

2.3 不同濃度IFNR和PP2的交互模型調控模式分析

通過同時擾動IFNR和PP2的初始濃度，研究IFNR和PP2的濃度，同時改變對細胞核中STAT1的同源二聚體和STAT3的同源二聚體濃度變化的影響，進而研究二者在干擾素-γ信號轉導過程中的協同調控作用。整理數據如表1、表2所示。

如表1所示，對照組中(STAT1N*)2的峰值為65nM。當干擾素-γ受體IFNR的濃度低于對照組濃度12nM時，磷酸酶PP2在濃度無論是高于或低于對照組濃度，通過模擬分析得到的(STAT1N*)2的峰值都低于65nM。當干擾素-γ受體IFNR的濃度高于對照組濃度的情況下，PP2在濃度高于對照值時，(STAT1N*)2的峰值低于65nM，PP2在濃度低于對照值時，(STAT1N*)2的峰值高于65nM。當PP2的濃度高于對照組濃度60nM時，IFNR的濃度無論是高于或是低于對照組濃度的情況下，通過模擬分析得到的(STAT1N*)2的峰值都低于65nM。當PP2的濃度低于對照組濃度的情況下，IFNR在濃度低于對照值時，(STAT1N*)2的峰值低于65nM，IFNR在濃度高于對照值時，(STAT1N*)2的峰值高于65nM。

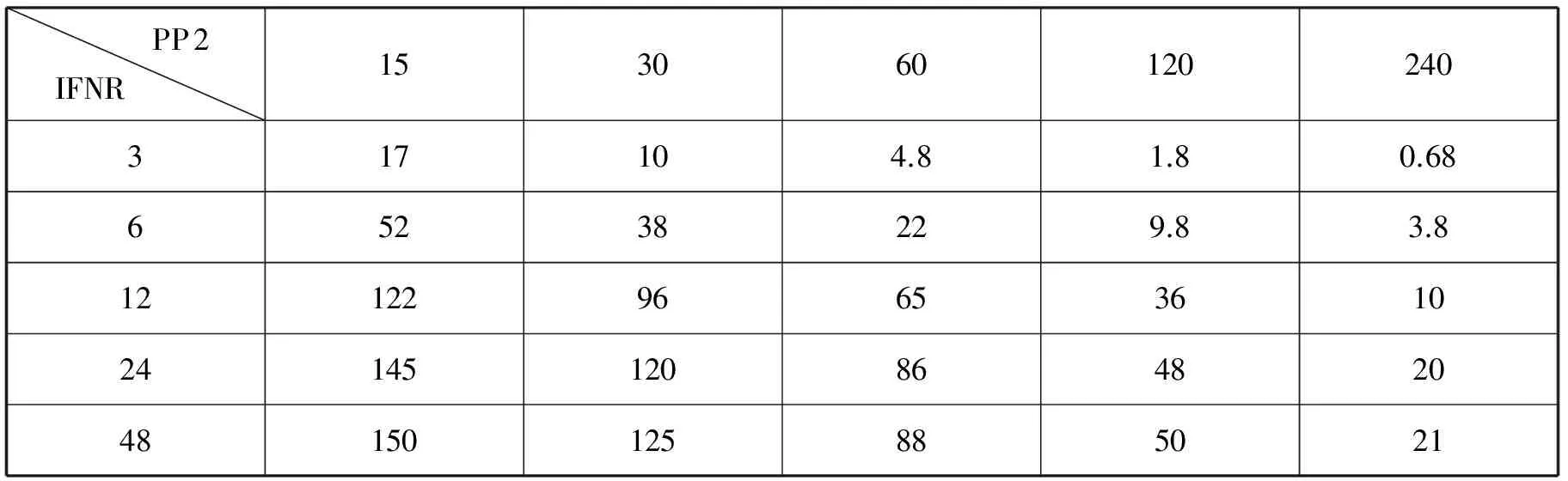
表1 不同IFNR和PP2的初始濃度對應的(STAT1N*)2濃度峰值

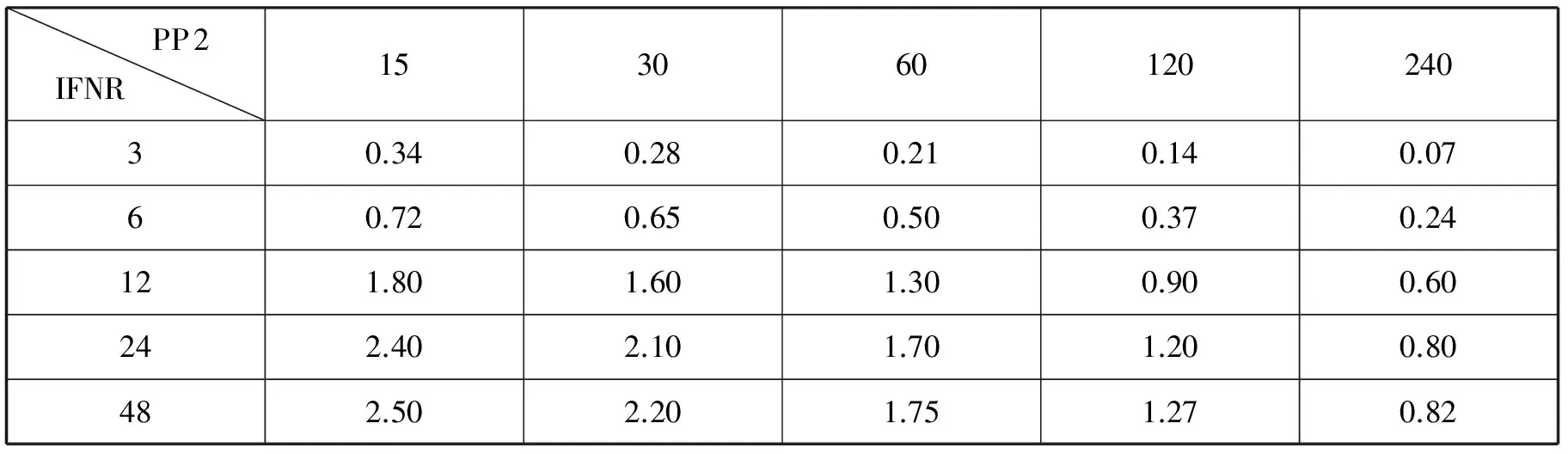
表2 不同IFNR和PP2的初始濃度對應的(STAT3N*)2濃度峰值

觀察表中數據后可知，(STAT3N*)2峰值的變化趨勢與表1中(STAT1N*)2峰值變化趨勢基本是一致的。

這些模擬結果表明，在干擾素-γ信號轉導的過程中，IFNR的濃度低于12nM時，IFNR的正反饋調節在干擾素-γ的轉導中占主導地位，而當PP2的濃度高于60nM時，PP2的負反饋調節在干擾素-γ的轉導中占主導地位。用統計學方法進行檢驗，得出(STAT1N*)2和IFNR、PP2的相關系數為0.594和-0.604，P值小于0.001，(STAT3N*)2和IFNR、PP2的相關系數為0.679和-0.485，P值小于0.001。結果表明，(STAT1N*)2和(STAT3N*)2的濃度與IFNR的濃度變化呈正相關，與PP2的濃度變化呈負相關。但同時擾動兩個影響因子的初始濃度時，標準回歸系數較單因子的標準相關系數有所變化，且極為顯著。

3 結論

本文采用系統生物學建模工具COPASI對干擾素-γ的信號轉導進行模擬，并應用統計學方法進行檢驗，通過模擬分別改變干擾素-γ受體和磷酸酶PP2的初始濃度,研究了二者初始濃度改變對胞核內STAT同源二聚體濃度變化的影響。通過同時改變二者的初始濃度，研究了二者濃度同時改變對細胞核內STAT同源二聚體濃度變化的影響，進而研究它們在干擾素-γ信號轉導過程中的協同作用。結果表明，改變單因子初始濃度時，細胞核內STAT同源二聚體濃度與R受體濃度呈正相關，且顯著性不明顯，與PP2濃度呈負相關，且顯著性明顯。二者協同作用時同樣與R受體濃度呈正相關，與PP2濃度呈負相關，但都極為顯著。因此推測，可以通過改變IFNR和PP2的初始濃度對干擾素-γ信號轉導過程進行調節，且二者協同作用時調控效果更明顯。本文對干擾素-γ信號轉導的調節機制進行了研究，有利于進一步研究干擾素-γ在抗微生物感染及免疫調節中的作用。

[1]徐強,王長亮,李勝.系統生物學——生命科學的新領域[J].中國醫藥報,2008,19(3):21-23.

[2]蔣太交,薛艷紅,徐濤.系統生物學——生命科學的新領域[J].生物化學與生物物理進展,2004,31(11):957-963.

[3]常暢.系統生物學的研究進展[J].生命科學研究,2006,35(2):81-83.

[4]譚初兵,杜冠華.系統生物學――藥物研發的新動力[J].中國新藥雜志[J].2006:123-128.

[5]Qing Y,Stark GR. Alternative activation of STAT1 and STAT3 in response to interferon-gamma[J].TheJournal of biological chemistry,2004,279(40):41679-41685.

[6]齊云峰.基于系統生物學方法的干擾素-γ和白介素-6信號轉導通路建模以及抗癌藥物誘導細胞凋亡機制的研究[D].長春：東北師范大學，2014.

[7]Yamada S,Shiono S,Joo A,etal. Control mechanism of JAK/STAT signal transduction pathway[J]. FEBS letters,2003, 534(1-3):190-196.

[8]Zi Z, Cho KH, Sung MH, etal. In silico identification of the key components and steps in IFN-gammainduced JAK-STAT signaling pathway[J].FEBS letters,2005,579(5):1101-1108.

[9]Rateitschak K，Karger A，Fitzner B，etal. Mathematical modelling of interferon-gamma signalling inpancreatic stellate cells reflects and predicts the dynamics of STAT1 pathway activity[J].Cellular signaling,2010,22(1):97-105.

[11]FISHER R A. The use of multiple measurements in taxonomic problems [J].Ann of Eugenics, 1936(7):179-188.

[12]徐群.非線性回歸分析的方法研究[D].合肥：合肥工業大學,2009.

[13]Hucka M，Finney A，Sauro HM，etal. The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models[J]. Bioinformatics, 2003,19(4):524-531.

[14]Achard F,Vaysseix G,Barillot E. Bioinformatics and data integration[J].Bioinformatics,2001,17(2):115-125.

[14]Mendes P. GEPASI: a software package for modelling the dynamics, steady states and control of biochemical and other systems[J].Computer applications in the biosciences,1993,9(5):563-571.

[15]彭司華,周洪亮,彭小寧,等.系統生物學的分析與建模[J].信息與控制,2004,33(4):356-363.

The IFN-γ Modeling Analysis of the Signal Transduction Model Based on the Systems Biology

QI Yun-feng, SUN Tian-tian, CHANG Hong-ling

(College of Life Science, Jilin Normal University, Siping Jilin 136000, China)

IFN-γ is a member of the family of the interferon in cytokine superfamily,it is a variety of biological functions such as microbial infection and immunity to adjust. Systems biology studies organism mainly adopt the method of system, the modeling and simulation of different levels of various signal transduction pathways and gene regulatory networks, etc. In this paper, the use of systems biology modeling tools COPASI to IFN-γ signal transduction were simulated, and the application of statistical methods, through the simulation respectively change the IFN-γ receptor (IFNR) and initial concentration of phosphatase PP2, studied the concentration change within the nucleus on the STAT homologous dimers the influence of the concentration change, by changing the initial concentration of both at the same time, studied the concentration change of The STAT in the nuclei of homologous dimers at the same time the influence of the concentration change, and then study them in the IFN-γ synergy in the process of signal transduction.

systems biology; IFN-γ; signal transduction

2016-04-26

國家自然科學基金項目“基于跨組學數據系統分析的表觀遺傳學藥物凋亡誘導建模研究”(31540035)；四平市科技發展計劃項目“組蛋白去乙酰化酶抑制劑誘導細胞凋亡機制建模研究”(2015062)。

齊云峰(1983- )，男，講師，博士，從事系統生物學研究。

Q811.4

A

2095-7602(2016)08-0056-05