基于非線性有限元算法的高壓電塔壽命預測

王偉

（廣西電力職業技術學院 廣西 南寧530000）

基于非線性有限元算法的高壓電塔壽命預測

王偉

（廣西電力職業技術學院 廣西 南寧530000）

針對高壓電塔在風載荷作用下的應力應變問題，提出一種基于非線性有限元的壽命預測算法。該算法根據高壓電塔高柔低質的結構特點，并結合平均應力動態模擬電塔在風載荷作用下的疲勞壽命，最終達到對高壓電塔的壽命預測。通過對220 kV高壓電塔的實證模擬，結果顯示：該算法的各階自振周期模擬誤差均小于5%，由Q420B型角鋼材質構成的電塔主懸桿疲勞壽命僅為54.15年。該算法對工程設計具有一定的指導意義。

非線性有限元；高壓電塔；風載荷；疲勞壽命

隨著我國電力事業的快速發展，遠程高壓輸電線路相繼建設并投入運行，高壓電塔故障的技術檢測成為了電力部門遇到的難題[1-2]。電力資源通過高壓電塔遠程傳輸供給區域電能使用，當高壓電塔發生倒塌或者傾斜等事故時，將導致大面積的區域斷電以及通訊不正常[3-4]。以往電力部門采用直升機巡檢，但是耗資較大[5]。因此，通過估計高壓電塔的使用壽命可以有效降低電塔損壞帶來的故障發生率[6]。

文中通過使用非線性有限元的方法對高壓電塔進行分析，結合平均應力修正得到風載荷狀態下的循環次數，從而動態模擬電塔在模擬電塔在風載荷用作下的應力應變，構造出高壓電塔的有限元節點處的疲勞壽命。最后對Q420B型角鋼和Q460T型鋼組成的220 kV高壓電塔的主懸桿、支護樁和塔頭進行實證分析。

1　高壓電塔非線性有限元建模計算原理

1.1非線性有限元理論

結構力學從本質上講是非線性的，而非線性由可以分為兩大類[7]：幾何非線性和材料非線性。本研究對高壓電塔采用材料非線性效應的應力應變，即工程應力描述材料非線性問題。由于高壓電塔裸露在露天中，因此不可避免的受到強風的應力影響，從而邊界條件隨著高壓電塔結構在強風速作用下引起非線性響應。假設非線性效應引起的位移分量是無限小量，假設高壓電塔的單位剛度陣為K，質量陣為M，風載荷矢量為f，則非線性有限元離散化的節點可由如下代數方程組表示[8]：

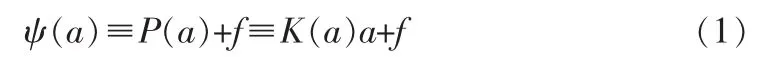
其中，a為高壓電塔對應位置的節點在風力影響下的位移向量。運用增量法求解代數方程組，將風載荷分為f0，f1，f2，…，在高壓電塔響應的節點的位移也分為a0，a1，a2，…。假定第m個風載荷fm與高壓電塔對應的位移am已知，只要每個風載荷增量Δfm足夠小，則可以利用fm+1=fm+Δfm去求解，am+1=am+Δam。

1.2風載荷的模擬

由于高壓電塔裸露在戶外，不可避免的受到風的影響。因此，風載荷的模擬是必不可少的。風一般在時間和空間上表現為風速與風向上[9]，將風載荷的靜力風和動力風作為高壓電塔應力應變的共同作用結果。平均風速和脈動風速構成了高壓電塔各節點所受到的瞬時風速，其中，平均風速為某時間段內空間某點各瞬時風速的平均值，脈動風速為某時刻空間某點瞬時風速與平均風速的差值[10]。計算高壓電塔某時刻t的某點的瞬時風速為[11]：

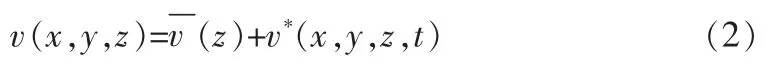
2　壽命預測與算法實現

2.1疲勞壽命

針對高壓電塔的應力應變問題，采用上述非線性有限元建模的方式識別風載荷譜對高壓電塔的各個節點回滯環數，從而得到風載荷應力幅下結構的循環次數。通過風載荷對高壓電塔的疲勞分析，得到各方向的平均應力和應力幅，利用平均應力修正公式得到等效應力幅，并得出與高壓電塔對應的節點的風載荷循環次數。對風載荷循環次數進行統計分析得到其中值，再利用S-N曲線模擬中值疲勞壽命。

考慮到風載荷的應力范圍閥值問題，采用平均應力修正的方式來描述高壓電塔的結構疲勞強度，平均應力影響因子λ為平均應力影響后計算得到的疲勞損傷度D0與不考慮平均應力影響計算得到的疲勞損傷度D的比值[13]，即

根據高壓電塔的鋼結構設計規范中關于構建和連接形式的分類，通過非線性有限元分析不同方向風載荷下的高壓電塔結構的應力幅和循環次數，按照Miner疲勞累計理論，計算高壓電塔的疲勞累計損傷[14]：

其中，k為風載荷塊的數量，ni為i塊風載荷應力幅作用下的實際循環次數，N為應力幅對應的高壓電塔材料壽命。

2.2算法的求解程序實現

高壓電塔在風載荷的作用下進行動態的非線性有限元分析，則可以利用Static Analysis改寫非線性有限元分析中的函數domain Changed（）和analyze（），同時，通過定義solve Curren Step（）和analysis Model Changed（）函數來實現對算法過程中不同節點位移的步驟管理，最后，利用有限元分析風載荷的循環次數計算高壓電塔的疲勞壽命。計算求解偽代碼步驟見如下：

Step.1：Static Analysis::domain Changed（）//建 立 函 數domain Changed；

Step.2：Static Analysis::analyze//函 數 的 有 限 元 分 析analyze；

Step.3：Clsaa FESolution Algorithm//求解非線性有限元；

Step.4：Von Mieses Material::Compute Constiitutive Matrix//計算疲勞壽命.

3　實證分析

3.1高壓電塔的有限元建模

本研究以220 kV輸變電工程酒杯形輸電塔為研究背景，電塔的呼高為32 m，塔全高為37 m，跟開8 m。塔身和橫擔的主材采用Q420B型角鋼，其他主材和橫隔采用Q460T型鋼，塔底部按固結處理。對高壓電塔采用非線性有限元離散化，產生655個節點和2 055個beam188梁單元，有限元模型如圖1所示。

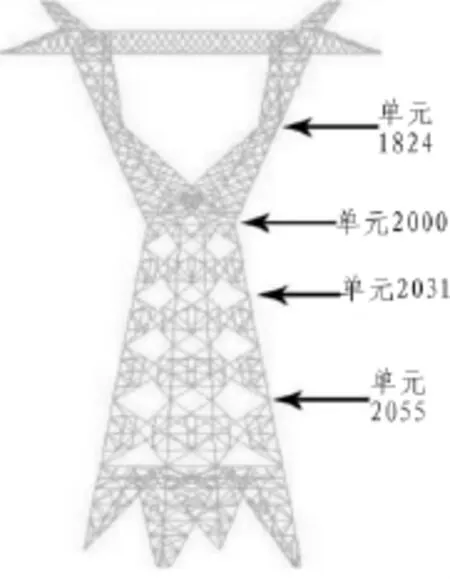
圖1　酒杯形高壓電塔的有限元建模

利用有限元分析軟件中分塊法對高壓電壓結構進行模態分析得到五階振型，結合公式（5），根據我國電力行業對高壓電塔實測研究，自振周期近似系數α=0.034。則五階振型如表1所示。

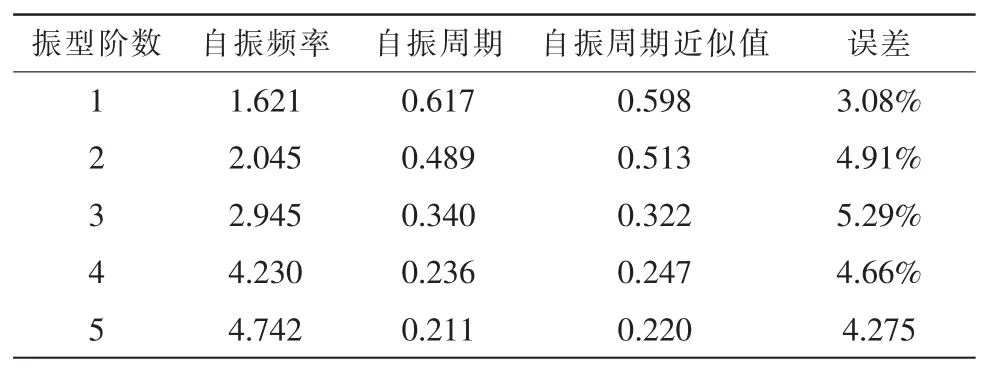
表1　高壓電塔的五階振型

由表1可見，非線性有限元建模算出的自振周期和結構自振周期誤差均小于5%，在允許范圍之內。說明了本研究利用的非線性有限元建模建立的高壓電塔比較準確。

3.2風載荷模擬

如圖1所示，由于主懸桿占據高壓電塔主要長度，因此在模擬時需要進行一次模擬點的劃分，即單元2031。利用Matlab程序分別對主懸桿（單元 2000-單元 2031-單元2000）、支護樁（單元1824-單元2000）和塔頭（小于1824單元）4個模擬點進行風載荷模擬。通過線性自回歸濾波器獲得響應的參數：1）平均風速取31.25 m/s；2）樁基粗糙度系數取0.005；3）計算的時間步長取0.1 s；4）頻率取0.01～10 Hz；5）計算振型階數取3階。3個模擬點的風載荷的功率譜如表2所示。由于高度愈高風速愈大，則功率譜愈大。由表2可見，高壓電塔的塔頭處所受到的功率譜在相同時刻處明顯大于主懸桿處。

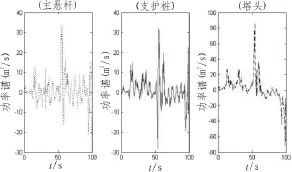
圖2　模擬處風載荷的功率譜

3.3動力學分析

根據風載荷對高壓電塔的應力應變的作用，將酒杯形電塔沿著豎向將32 m呼高等分為10段，采用非線性有限元時程分析法，以自重作用下的分析結果做為初始狀態，分別計算每段的風載荷，然后平均分到高壓電塔的節點上，最后將每個節點上的風載荷疊加得到電塔節點的風載荷的非線性動力模擬。

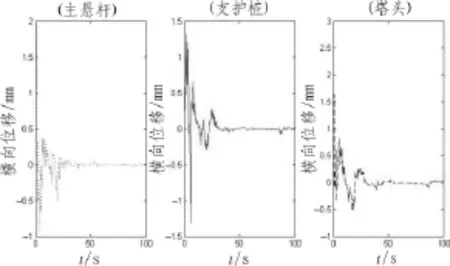
圖3　模擬點處風載荷作用下的橫向位移

由圖3可得，在風載荷的應力應變作用下，高壓電塔的橫向最大位移出現在塔頭處在2 s時刻，其最大位移值為3.0 mm。對應的計算beam188梁單元的應力均值與應力幅對應的風載荷循環次數，如表2所示。

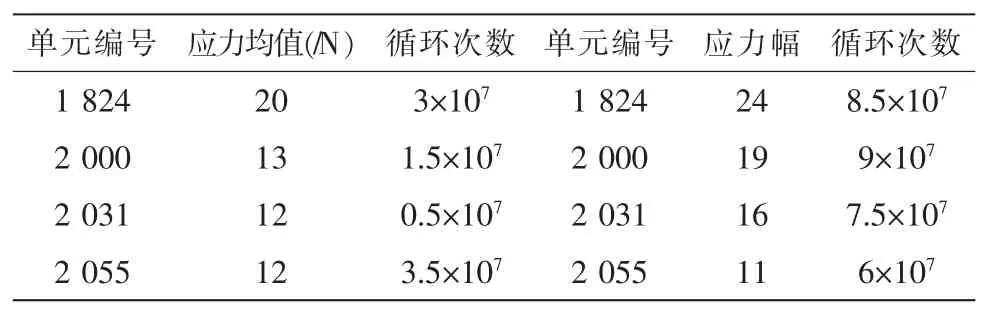
表2　模擬點的風載荷循環次數

3.4壽命預測

采用冪函數的方式將S-N曲線對應的經驗方程取對數整理后可得lgN=a+blgD，其中 a和 b為 Q420B型角鋼和Q460T型鋼常數（a=lg3.12e10，b=-lg3.02）[15-16]。對高壓電塔的4個模擬單元點進行疲勞壽命分析，如表3所示。

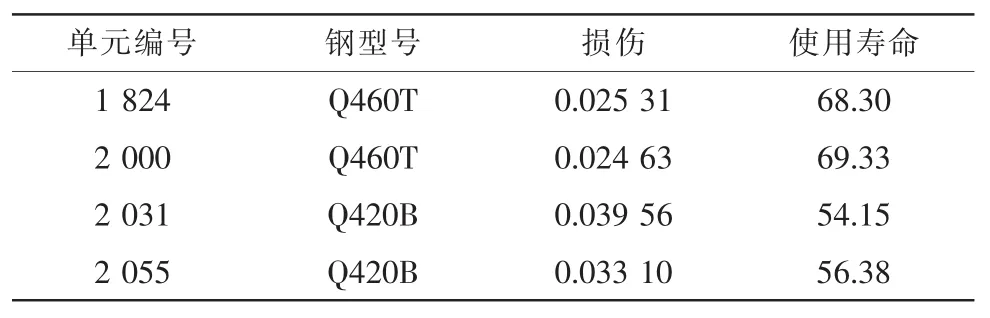
表3　高壓電塔的疲勞壽命

由表3可見，主懸桿（單元2000-單元2031-單元2000）疲勞壽命的最小值為54.15年，而支護樁（單元1824-單元2000）和塔頭（小于1824單元）的疲勞壽命最小值為68.30年。

4　結　論

本研究提出了求解高壓電壓使用壽命的非線性有限元算法，該算法動態模擬了高壓電塔在風載荷作用下的應力應變問題，結合平均應力修正公式得到了高壓電塔在有限元節點單元處的疲勞壽命。通過選用220 kV的高壓電塔進行實證模擬，結果顯示各階自振周期模擬誤差均小于5%，與此同時，電塔的疲勞壽命最小值出現在Q420B型角鋼的主懸桿部位，其疲勞壽命為54.15年。該算法可以作為電力部門對高壓電塔使用壽命的預測分析，對實踐具有一定的意義。

[1]王越勝，陳星.高壓電塔傾斜數據監控系統設計[J].杭州電子科技大學學報，2012，32（5）:247-249.

[2]陸竑.風光互補供電在輸電線路視頻監控系統的應用研究[J].節能，2014（6）:63-66.

[3]戴靠山，王健澤，毛日豐，等.一種風電塔架減振耗能裝置的振動臺試驗研究[J].地震工程與工程振動，2014（1）: 868-872.

[4]鄭松濤，湯文成，陳昀.SLP法在風電塔筒廠區總平面布置中的應用[J].工業工程與管理，2010，15（1）:116-120.

[5]楊勐，王瑋，倪平浩，等.智能輸電線路遠程在線監測技術的相關研究進展及發展趨勢[J].電氣應用，2012（5）:20-24.

[6]張鵬林，曹力，劉九逍，等.風電塔筒在三種工況下的靜動態研究[J].機械設計與制造，2013（10）:200-202.

[7]李志威，劉明軍，劉騰澳.基于非線性有限元的可變形模型的變形方法[J].計算機應用.2013，33（3）:684-687.

[8]蔡勇，李光耀，王琥.GPU通用計算平臺上中心差分格式顯式有限元并行計算[J].計算機研究與發展，2013，50（2）:412-419.

[9]余娟，余明友，金建偉.風載荷作用下天線支撐桿穩定性分析[J].軟件導刊，2013，12（4）:49-51.

[10]潘登，祁文軍，宋長飛，等.基于VB設計的風能資源評估軟件[J].計算機光盤軟件與應用，2012（2）:177-178.

[11]劉章軍，萬勇，曾波.脈動風速過程模擬的正交展開-隨機函數方法[J].振動與沖擊，2014，33（8）:120-124.

[12]徐培福，肖從真，李建輝.高層建筑結構自振周期與結構高度關系及合理范圍研究[J].土木工程學報，2014（2）:1-11.

[13]王文濤，上官文斌，段小成，等.基于線性疲勞累計損傷橡膠懸置疲勞壽命預測研究[J].機械工程學報，2012，48（10）:56-65.

[14]紀冬梅，軒福貞，涂善東，等.基于支持向量機的P91鋼蠕變-疲勞壽命預測[J].壓力容器，2011，28（10）:15-21.

[15]孫毅杰，李永祥，張杰新.Q420B高強度角鋼工藝研究與控制[J].煉鋼，2011，27（4）:29-32.

[16]黃偉兵.電力鐵塔專用角鋼性能研究[D].南昌：南昌大學，2011:42-44.

Predict the life of high-voltage tower based on the nonlinear finite element method

WANG Wei
（Guangxi Electric Power Vocational Technology College，Nanning 530000，China）

For high-voltage tower under wind stress and strain problems loads，made life prediction algorithm based on nonlinear finite element.The algorithm based on the structural characteristics of high-voltage tower soft low-quality，and combined with the average stress dynamic simulation electrical tower under wind loads of the fatigue life.It ultimately achieved the high-voltage tower life prediction.Finally，220KV high-voltage tower empirical simulation results show that:each step of the algorithm natural cycle simulation error is less than 5%，the main angle from the Q420P type material constituting the suspension rod fatigue life of only 54.15 years.This algorithm has some guiding significance for engineering design.

nonlinear finite element；high-voltage tower；wind load；fatigue life

TN06

A

1674－6236（2016）21-0018-03

2016-03-13稿件編號：201603153

國家自然科學基金項目（50767001）

王 偉（1982—），男，山東威海人，工程師。研究方向：高壓輸電線路施工檢修。