含能材料物理化學性能理論預估研究進展

嚴啟龍，宋振偉，安 亭，張曉宏，趙鳳起

(西安近代化學研究所燃燒與爆炸技術重點實驗室，陜西 西安 710065)

?

含能材料物理化學性能理論預估研究進展

嚴啟龍，宋振偉，安 亭，張曉宏，趙鳳起

(西安近代化學研究所燃燒與爆炸技術重點實驗室，陜西 西安 710065)

從含能材料領域的最近發展成果出發，討論了該領域的主要研究方向,重點論述了當前含能材料物理化學性能理論預估的最新成果，主要包括量子化學、分子動力學或者半經驗QSPR建模的方法預估含能材料的感度、燃燒爆轟性能、反應活性、固化機制與力學性能的研究進展。總結了目前存在的主要技術壁壘，包括缺乏完備統一的含能材料性能標準實驗數據庫，沒有自主知識產權的商業化含能材料性能計算軟件，且國際上商業軟件對含能材料的物理化學性能的可靠預測僅局限于爆轟性能和燃燒性能。文獻調研表明，我國需要進一步加強該領域研究，最終建立一個能評價含能材料性能與安全的綜合軟件平臺。附參考文獻90篇。

含能材料；物理化學性能；理論計算；量子化學；分子模擬

引 言

鑒于國防的重要性，世界各國對研發新型含能材料進行了長期持續的投入。至20世紀70年代，已基本形成了獨立的含能材料學科體系(國內專業名稱為軍事化學與煙火技術)，并成為軍械武器系統技術的重要支撐。尤其是自20世紀90年代以來，隨著世界局勢的緊張變化及軍事工業的發展，作為武器系統最重要的動力和毀傷能量源的含能材料得到了迅猛發展。調查表明[1]，近年比較活躍的含能材料研究方向包括：含能化合物的分子設計、含能材料納米化、共晶化與表面改性、含能材料熱分解、點火燃燒和爆轟、極限條件下含能材料的響應、含能材料配方設計及工程化應用、含能材料安全性能與綠色利用及含能材料物理化學性能理論預估(包括量化計算、多尺度分子模擬)等。本文簡要總結了含能材料物理化學性能理論預估方面的最新研究進展。

1 含能材料感度預估

含能材料在受到撞擊、摩擦、靜電火花或沖擊波等刺激時，容易發生燃燒或爆炸[2]。撞擊感度是評判炸藥安全性的主要指標，在理論和工程應用中具有重要意義[3]。解決炸藥感度理論判據問題，僅靠量子化學的方法是不夠的[4]。炸藥在外界刺激作用下發生爆炸是一個十分復雜的過程，涉及機械、物理和化學等諸多因素[5]。在同類刺激源作用下，由于炸藥的摩擦系數、彈塑性、硬度和模量等性質不同，炸藥所吸收的機械功也不同。即使在炸藥吸收的機械功相同的情況下，由于炸藥的熔點、熔化焓、比熱、導熱系數等參數不同，炸藥內所產生的熱點溫度也不同。只有在熱點臨界尺寸、溫度，以及持續時間相同的情況下，炸藥發生爆炸的難易程度才取決于該分子的反應活性，即可通過量子化學計算的結構參數和熱力學數據表征。然而，科研人員最感興趣的是決定安全性能的分子反應活性[6-8]。肖鶴鳴課題組[9]成功運用量子化學方法，完成諸多開拓性的工作。近來他們又對含能混合體系分子間的相互作用展開了探索，以期對高聚物黏結炸藥或固體推進劑的配方設計提供一定的理論指導[10]。

撞擊感度通常采用落錘實驗法獲得，它以在常壓室溫(20℃)下、特定質量的落錘作用下含能材料的爆炸概率(百分比)或50%爆炸概率下的特性落高H50來表征(勢能值)[11]。然而此類實驗存在一定局限性：(1)實驗具有危險性；(2)實驗結果受外界條件和人為因素影響，重復性差；(3)無法通過實驗獲得新含能材料的撞擊感度。因此，完全靠實驗來確定含能材料的H50已不能滿足日益劇增的新型含能分子設計的需要[12]，有必要根據理論方法對含能材料的撞擊感度進行預估。首先，物質結構可決定其性質，同時物質性質可反映其分子結構。尋求撞擊感度與炸藥分子結構參數之間的關聯已成為當前炸藥撞擊感度理論研究的一個重要方向[13]。國內最初的研究主要以硝基含能材料等簡單分子的撞擊感度預測為主，提出相關的計算原理和方法[14]。國際上有關撞擊感度與結構的研究最早始于20世紀中葉，Bowden等[15]對含能材料撞擊感度與其晶體結構之間的關系作了探討。Delpuech等[16]首先發現了仲硝基類含能材料的沖擊波感度和熱穩定性與其分子電子結構、以及C-NO2或N-NO2鍵能之間存在重要的關聯性。Kamlet等[17]則提出了一種基于氧平衡估算撞擊感度的方法。通過多年的發展，形成了以下幾種主要的撞擊感度理論預測方法[18]。

1.1 量子化學方法(QM)

量子力學理論的不斷完善，尤其是自洽場方法與密度泛函理論(DFT)的建立與完善，及高速計算技術的發展，使得人們能夠借助高水平量子化學方法在微觀結構層面上研究物質結構與性質的內在聯系。撞擊感度的量子化學理論研究也隨之得到了發展。Politzer等[19]通過對CaHbNcOd炸藥量子化學計算，發現靜電勢等分子結構參數與其撞擊感度存在一定的相關性。近期，他們又發現撞擊感度與其晶格的可壓縮性或晶體內自由體積存在重大關聯，同時也證實了關于含能材料晶體空穴受沖擊壓縮時產生熱點的起爆理論[20]。Keshavarz等[21]在此基礎上也進行了相關研究，發現C-NO2鍵區域的靜電勢在一定程度上反映了其不穩定性，從而用于標識其敏感度[22-23]。Liu等[24]則證實了硝基化合物中硝基的電荷值決定了高能材料的機械感度。Mullay等[25]也發現不含羥基的18種硝基芳香化合物的撞擊感度與C-N鍵的近似靜電勢值存在較大相關性。Ren[26]進一步發現可由分子的靜電勢獲得環狀結構炸藥分子，如硝基環丙烷、環丁烷硝基、硝基環戊烷和硝基環己烷等的撞擊感度。Rice和Hare[27]則選取了化學鍵中點處的靜電勢近似值作為關聯值，用以計算CaHbNcOd含能分子的撞擊感度和爆熱。而Politzer等[28]則認為撞擊感度與含能材料的理論最大爆熱存在必然聯系，而與爆速、爆壓的關聯性小。而根據熱點起爆理論，所有的失控化學反應都始于熱點引發的分解反應。Zohari等[29]的研究表明，CaHbNcOd系列含能分子的撞擊感度不僅與H/O摩爾比有關，還與熱分解活化能存在明確的關系。依據這一觀點，Mathieu等[30]通過分解反應速率常數估算了硝基化合物的H50值，所得結果與實驗值非常接近(相關系數約為0.8)。該結果表明含能材料的感度取決于在熱點分散前分解反應的自蔓延能力。此外，Tan等[31]研究表明，相對上述決定性因素，取決于含能材料分子的化學鍵與非鍵耦合(應變能)的分子剛度對其感度的影響最大。結合以上多種因素，Keshavarz[32]開發了一套可以計算含能材料機械感度的Visual Basic程序，對硝基吡啶、硝基咪唑、硝基吡唑、硝基呋咱、硝基三唑、硝基嘧啶、多硝基芳烴、苯并呋咱、硝胺，硝酸脂、含其他官能團硝基脂肪族和硝酸高能化合物的撞擊感度計算精度較高。他們的預測結果對Mullay等[33]關于CaHbNcOd炸藥撞擊感度與分子內部電荷不平衡程度的相關性模型給予了支持。Mullay的表面靜電勢參量模型有5個: 模型1采用每個鍵中點的靜電勢的近似值來計算感度；模型2應用等靜電勢面上正電荷與負電荷平均值的差值來計算感度；模型3應用與靜電勢相關的統計參量(平衡參數ν)來計算感度；模型4運用單分子量子化學信息來估算其爆熱Qdet，然后通過爆熱來計算撞擊感度；模型5用平衡參數ν與爆熱結合來計算撞擊感度；對于硝胺化合物，在熱源、沖擊波和機械撞擊所引發的分解過程中，雖然在一些情況下會存在其他起主導作用的反應路徑，但N-NO2的斷裂仍然看做初始反應步驟。Edwards等[34]同樣采納了模型4，并輔以PM3和DFT兩種級別量子化學方法來計算幾種硝胺炸藥的爆熱。他們發現，在DFT理論水平，感度隨著最高占有軌道(HOMO)和最低空軌道(LOMO)能量的增加呈指數遞減。張朝陽等[35]也在DFT理論計算的基礎上，發現撞擊感度與硝基所帶電荷之間存在較大的相關性。他們采用廣域梯度近似(GGA)的方法，基于Beck 混合泛函計算了硝基上的Mulliken電荷，并與硝基化合物的撞擊感度進行關聯。結果表明，當硝基上的負電荷小于0.23 時，該化合物較為敏感，即H50≤40 cm (2.5 kg)。因為硝基所帶電荷值可用來估算鍵能、氧平衡和分子靜電勢等一系列結構參數，且硝基上的Mulliken凈電荷越多，該分子就越鈍感。需要指出的是，他們的方法僅適用于含有弱鍵C-NO2、N-NO2或O-NO2的硝基化合物。

1.2 定量結構-性質相關性法(QSPR)

QSPR通過選用合適的分子結構來描述分子的結構特征，結合各種統計建模工具，研究有機物的結構與其各種物理化學性質之間的定量關系。分子結構可用反映其特征的各種參數來描述，即有機物的各類性質都可以用化學結構的某個函數來表示。通過對分子結構參數和所研究性質的實驗數據之間的內在定量關系進行關聯，建立分子結構參數和性質之間的關系模型。可靠的定量結構-性質相關模型可用來預測尚未合成的化合物的各種性質。Nefati等[36]首次嘗試了用人工神經網絡方法來預測含能材料的撞擊感度。他們選取204個含能材料分子作為樣本集，同時設置了3類共39個描述參量來表征其分子結構(包括拓撲參量、幾何構型參數和電子參數)。通過計算這204個含能化合物的39個結構參數，并對它們進行自由組合。然后經過多元線性回歸(MLR)、偏最小二乘法(PLS)和BP神經網絡法(BP-ANN)等算法，最終確立了撞擊感度的預測模型。研究結果表明，相對傳統的線性方法，使用非線性神經網絡方法(MLR和PLS)可獲得更優化的模型。最佳的神經網絡模型共采用13個參數作為輸入神經元，包括隱含層的2個神經元。在Nefati等人的研究基礎上，Cho等[37]做了進一步的優化和改進，并預測了234種含能化合物的撞擊感度。他們選取了與文獻[36]不同的參量來描述含能化合物的結構，并根據參數種類和不同組合將它們分成7個子集。通過構建3層BP神經網絡結構，對每個描述參量子集進行建模。結果發現，最好的網絡結構為17-2-1，即采用含分子組成及拓撲類型的17種分子參量作為輸入層變量，神經網絡結構隱含層需包含2個神經元。他們指出，包含分子組成及拓撲描述符的子集比含有電子參數如LUMO、HOMO和偶極矩的子集能獲得更精確的預測結果。Wang等[38]則進一步利用遺傳算法和基于電拓撲態指數的人工神經網絡方法的QSPR模型預測了非雜環硝基化合物的撞擊感度，獲得的最佳BP神經網絡結構為16-12-1，預測結果與實測值最接近。

隨后，Keshavarz等[39]僅選取了10個比較重要的分子結構特征參數，并利用神經網絡算法通過MATLAB編程，預測了大量CaHbNcOd炸藥分子的感度。結果表明，該模型通過275個實驗樣本訓練后得到了最優化網絡結構，大幅提高了其計算精度，明顯優于Rice等[27]采用5個量子化學模型所預測的結果。此外，王睿等[40]選用原子型電性拓撲狀態指數，表征了20種均三硝基苯類含能化合物。他們采用MLR方法進行擬合，所創建的4參數線性模型預測效果較好。隨后，他們在此基礎上采用原子電性拓撲狀態指數和基團電性拓撲指數共同來表征包括硝基芳香化合物、硝酸酯和硝胺在內的41種含能硝基化合物的分子結構[41]。并采用逐步回歸MLR法成功建立了5變量線性預測模型。初步研究表明，電性拓撲狀態指數不僅可以反映硝基含能化合物的拓撲結構，還包含了其分子中電子狀態。為了擴大樣本數，他們還采用156個硝基非雜環含能化合物進行訓練標定，形成了基于MLR、PLS和BP神經網絡等3種建模方法的預測模型。結果表明，非線性的BP神經網絡方法構建的預測模型無論在穩定性、內部及外部預測能力以及泛化性能方面都優于線性方法(MLR與PLS)。近來，Morrill等[42]則利用該軟件在AM1半經驗水平計算了227個化合物的結構參數，然后結合軟件集成的最優多元線性回歸(BMLR)算法，從大量算符中篩選出8個并建立線性模型，取得了較好的結果。肖鶴鳴等[43]采用HMO、CNDO/2、MINDO/3和MNDO等分子軌道算法，對苯、甲苯、苯胺及苯酚等4類分子的硝基衍生物進行了系統研究。結果表明，對結構相似物，其分子中最弱鍵的鍵級(如π鍵、Mullikan鍵或Wiberg鍵)或雙原子作用能與其撞擊感度或熱安定性之間存在漸變關系。因而，根據炸藥熱分解和起爆機理，他們提議以基態分子最弱鍵的鍵級或該鍵所連接的兩原子之間的相互作用能作為判據來判別同系物炸藥的熱安定性或撞擊感度的相對大小。判斷方法有兩種:(1)由II級鍵估算化學鍵的離解能來判別；(2)根據鍵級和雙原子作用能的線性相關性來判斷。這些研究對炸藥的撞擊感度影響因素有更深層次的認識，對炸藥其他爆炸性能的預測也有重大的指導意義。

Kim等[44]根據范德華分子表面靜電勢(MSEP)的定量結構-性質關系(QSPR)更精確地預測含能材料的撞擊感度。他們從MSEP衍生的各種三維描述，利用總和為正MSEP的變化，并結合其他3個參數，確立了新的QSPR方程。在此基礎上建立了如下6種不同精度的模型：

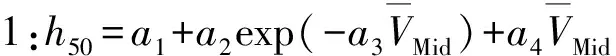
(1)

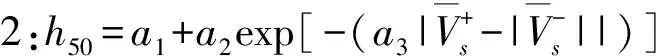
(2)

模型3:h50=a1+a2exp(a3υ)

(3)

模型4:h50=a1+a2exp[-a3(Q-a4)]

(4)

模型5:h50=a1exp[a2υ-a3(Q-a4)]

(5)

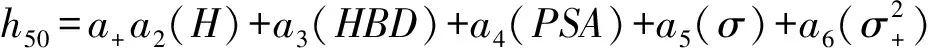
(6)

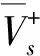
(7)

(8)

(9)

(10)

從以上表達式可以看出，含能化合物分子表面電荷分布與其撞擊感度大體呈指數關系，而大多數QSPR研究所得的結論是簡單的線性關系。綜上所述，量子化學方法可提供精確的結構數據，但是需要耗費大量的CPU時間，對計算機硬件要求較高。而QSPR方法則可以系統全面地描述含能材料分子結構參數與其撞擊感度之間的內在聯系，并建立相應的預測模型。但是，一般采用的描述參量精度都集中在經驗、半經驗水平，精確度稍差。同時，QSPR方法所需要的實測感度訓練數據源差別較大、可靠性不能得到保證，給研究帶來了一定的不確定性。在確定新含能化合物的撞擊感度后，可以進一步確定其靜電火花感度，因為根據熱點起爆理論，這兩者本質上存在一定的相關性[45]。盡管如此，含能材料的靜電火花感度產生機制還有待于進一步驗證。

2 含能材料燃燒性能預估

含能材料的燃燒性能預估主要采用綜合性預估軟件ALE3D[46]。該軟件是利用任意拉格朗日-歐拉(ALE)技術進行多物理場數值模擬計算的重要工具。它通過采用混合有限元和有限體積非結構化網格來解決二維或三維流體的彈塑性響應問題[47]。相比局限于拉格朗日或歐拉(平流)的工具，ALE和網絡松弛方法的引入拓寬了其應用范圍。同時，在多物理場和復雜幾何形狀下能保持高精度模擬和高效率運算。除了用作流體力學和結構化學計算，ALE3D還可通過用戶分工合作方式整合各種嵌套軟件，因而具備多物理場模擬的能力。ALE3D附加的功能包括熱傳導、化學動力學和擴散傳質、不可壓縮流體、廣泛的材料模型、化學反應模擬、多相流、以及磁流體力學(隱式)、短(顯式)時間尺度方面的應用[48-49]。可模擬爆轟、爆燃、對流燃燒，主要針對高能炸藥和推進劑的熱、機械刺激響應[50-51]。它用有限元法增強動量守恒，使很多實際問題可由“拉格朗日+重映射”法來解決，還允許用戶在全拉格朗日法或全歐拉法模式下運行。它可以通過任意拉格朗日-歐拉計算，模擬含能材料斷裂和戰斗部破片過程，從而準確模擬殼體材料的表面形貌及其變化。

對于傳熱過程，ALE3D主要用于鋁合金制造行業。它通過繪制溫度曲線來描述從鋁合金板坯傳熱到滾筒過程中的溫度分布，這可以分析鋁板內應力松弛率[52]。除了集成材料復雜損傷演化模型，ALE3D代碼還可模擬表面摩擦滑動和接觸熱阻抗。同時，可以模擬炸藥爆炸沖擊波和鋼筋混凝土柱接觸時的復雜相互作用，ALE框架內允許完全耦合的流固耦合法。其中磁流體動力學(MHD)模塊能解瞬態磁場對流擴散方程、磁力與流體力學耦合方程、焦耳熱與傳熱耦合方程等。它采用單胞為中心的戈東諾夫型有限體積法來模擬多相或多個分散物質，每個階段都擁有其特定的速度和狀態參數，其中每個階段都被視為連續流體[53]。

對于推進劑燃燒性能(主要是能量性能和燃速)的計算還有幾種軟件：如美國的NASA-CEA、葡萄牙的THOR、加拿大的CERV、德國的ICT熱力學代碼、俄羅斯的REAL等，它們可對雙組分及以上的推進劑進行循環計算，采用標準試樣驗證其精確度[54-55]。這些代碼都是以熱力學計算為基礎，在既定燃燒產物的前提下進行的計算，其精度取決于材料的組分[56-57]，對含金屬燃料、尤其是含有機金屬化合物的配方計算誤差較大。

3 含能材料爆轟性能預估

含能材料的爆轟性能與爆熱密切相關，而爆轟過程的反應熱可由爆轟反應產物的生成熱(HOFs)直接求得。通過選用適當的方法，準確計算含能材料分子的生成熱是量子化學的主要優勢。最早使用半經驗分子軌道方法(如MNDO、AM1、PM3等)可以快捷地計算生成熱[58]。但這些半經驗方法主要依據一些代表性小分子和烴類的熱力學和光譜數據進行參數化，對含多種取代基或特殊結構的高能量密度材料，生成熱的計算往往存在較大誤差。一些采用改進的半經驗方法如成對距離定向高斯修正法(PDDG)可減少誤差[59]。對622個含CHNO化合物的生成熱計算表明，理論值與實驗值的絕對誤差由PM3法的21.3 kJ/mol下降至PDDG/PM3方法的13.4 kJ/mol[60]。

隨著計算技術的發展，能夠實現對絕大多數高能量密度材料的第一性原理計算。因此半經驗方法已逐漸被第一性原理方法所代替。但第一性原理只能求分子的總能量，而無法直接計算生成熱。這就需要設計等鍵反應，利用參考物的實驗生成熱，借助Hess定律，求得目標分子的生成熱。在等鍵反應中，反應物和產物的電子環境相近，電子相關能造成的誤差可以大部分抵消，可大幅降低計算的生成熱誤差。在設計等鍵反應時，通常根據鍵分離規則(BSR)把分子分解成一系列與所求物質具有相同化學鍵類型的小分子(已知生成熱的參考物)。為進一步減少誤差，應盡量保持母體骨架或原有分子的化學鍵。由下列公式：

ΔH298=∑ΔfHP-∑ΔfHR

(11)

ΔH298=ΔE298+Δ(PV)=ΔE0+ΔZPE+

ΔHT+ΔnRT

(12)

式中：∑ΔfHP和∑ΔfHR分別為298K下等鍵反應產物和反應物的生成熱之和；ΔE0和ΔZPE分別為0 K時產物與反應物的總能量和零點能(ZPE)之差；ΔHT為從0 K到298 K的焓值溫度校正項；Δ(PV)在理想狀態條件下為ΔnRT；對于等鍵反應，Δn=0，故Δ(PV)=0。

聯立上述兩式，可由參考物的生成熱求得目標分子的氣相生成熱。第一性原理計算方法很多，但對高能量密度材料計算方法很有限。雖然閉合層的限制性Hartree-Fock(HF)方法可得到準確的分子幾何構型，但所得分子能量與實驗誤差通常在200kJ/mol以內，且個別誤差高達700kJ/mol。因HF方法忽略了電子相關效應，導致能量值出現系統正誤差。為此，可用微擾法(MP2和MP4等)、多組態法(如CISD、CCSD和CASSCF)及DFT法(如B3LYP、B3PW91)校正電子相關效應。微擾法和DFT法能量誤差通常在40kJ/mol以內，而多組態法誤差一般小于5～8kJ/mol[61]。然而，多組態法對中等體系的計算量也非常大，因此通常用DFT方法處理電子相關效應。雖然DFT方法的能量絕對誤差較大(40kJ/mol)，但是由于生成熱的計算是通過設計等鍵反應來實現的，反應物與產物的能量誤差大部分相互抵消，即生成熱的真實誤差通常比40kJ/mol小得多。關于DFT具體泛函的選用，通常要以同類型化合物的準確實驗生成熱為基準，比較并檢驗各種泛函計算結果對該類化合物的準確性，以確定最佳方案。

量子化學計算得到的是氣相生成熱，結合遺傳算法(Genetic Algorithm, GA)、靜電勢法和神經網絡法(Neutral Network, NN, 例如Back-propagation Neural Networks, BPNN)等手段，計算固體升華熱后即可求得固相生成熱。舒遠杰等[62]采用上述方法對72種籠狀和橋環類分子的固態標準生成熱進行計算，結果表明，其標準誤差約為20.9kJ/mol。相對于第一性原理，靜電勢法因其物理意義明確、結果誤差小，在高能量密度材料升華熱計算中得到了廣泛應用[63-64]。對于有機分子所組成的固體而言，其升華熱取決于分子間相互作用能，相互作用能越大則升華熱越大。因此，升華熱與分子表面靜電勢有關。由靜電勢求得升華熱的原理及相關公式可參見文獻[65]。

目前，基于1384個化合物(含172個化學基團)的升華熱，建立了3層前饋神經網絡(feed forward neural network)計算模型[66]。采用該模型計算的升華熱值與實驗結果的相關系數平方、平均誤差和均方根誤差分別為0.9854、3.54%和4.21kJ/mol[67]。后者明顯小于靜電勢法所得誤差(11.7J/mol)，具有一定的普適性和精確性。但由于樣本極少涉及高能量密度材料分子，且高能量密度材料的特殊性(強分子內基團的相互作用、較大環張力等)，該方法是否能準確預測其升華熱還有待檢驗。在獲得生成熱后，如果已知高能量密度材料分子的密度，即可由Kamlet經驗公式預測其爆速和爆壓[68]。此外，基于化合物優化構型，用Monte-Carlo方法求得分子周圍0.001e/bohr3等電子密度面所包圍的體積，即可求得摩爾體積(V)。因該法求得的體積值波動范圍較大，通常要取重復100次以上的平均值。由分子質量與平均摩爾體積之比可計算該分子的理論密度(ρ)。研究表明，在B3LYP/6-31G**水平下計算的理論密度與實測值吻合度較好[69]。將所求得的生成熱及密度值代入Kamlet公式，即可得到單質含能材料的爆速和爆壓。第一性原理計算結合等鍵反應不僅可求得生成熱，還可計算基團相互作用能和環張力，從分子水平闡明結構與性能的關系。當然，計算目的不同，所設計的等鍵反應也不同。

為了有效地預估新含能材料及其配方的性能，科研人員一直在探索精確計算爆轟參數的算法和軟件。除了最早Rothstein(1979和1981年)和Kamlet(1968年)分別創立的簡便方法之外，目前已經發展建立了一系列更精確的狀態方程。通常，熱化學計算比量子化學計算更加便捷、成本較低、且準確性和可靠性也越來越高。比較常用的熱力學代碼有BKW-Fortran、ARPEGE、Ruby、TIGER[70]、CHEETAH、EXPLO-5、MWEQ、BARUT-X和ZMWNI[71]。目前，美國的TIGER和CHEETAH及克羅地亞的EXPLO-5是被廣泛使用的3種預測推進劑和炸藥性能的可靠熱化學代碼。它們都可以由研究人員來任意增添組分或改變配方，以優化所設計產品的性能。最新版本的CHEETAH 7.0是通過美國能源部和國防部與澳大利亞防御局(DSTO)武器發展與防御數據相互交換協議下共同開發的[72]。然而，CHEETAH不僅用于高能炸藥的爆轟參數計算，還可以預測許多復雜材料的熱力學行為，包括塑料、有機液體混合物、固-液混合物等在沖擊波、激光或地球內部等極端條件下的性能。CHEETAH通過不斷拓展其功能，最新版本可以模擬化學和物理動力學，與先進的流體力學聯合使用可解決復雜高能材料體系很多應用基礎問題。TIGER和CHEETAH都是源于美國的Ruby和BKW。目前，美國已將這兩個軟件內部合并為CTH-TIGGER。新代碼包含了H2O的最新狀態方程，并新增了200多種離子化合物相關數據。

EXPLO-5是基于化學方程式、生成熱和密度，預測高能炸藥、推進劑和煙火藥爆炸參數的一款熱化學計算程序。EXPLO-5在含能材料的合成、配方優化和數學建模中是一個非常重要的工具。EXPLO-5運用自由能最小化方法在指定的溫度和壓力下計算平衡組成和熱力性質，數據結合Chapman-Jouguet爆炸理論，能夠計算爆炸參數，如爆速、爆壓、爆熱和爆溫等。從平衡組成到熱力學狀態參數和等熵膨脹，軟件通過內置擬合程序計算Jones-Wilkins-Lee (JWL)狀態方程中的系數。通過解樣品的熱力學方程和恒壓燃燒條件下的守恒方程來預測固體推進劑的燃燒性能，如比沖、推力系數和定容推力等。該程序采用氣態爆轟產物的Becker-Kistiakowsky- Wilson(BKW)狀態方程和Jacobs-Cowperthwaite- Zwisler (JCZ3)狀態方程、理想氣體方程、維也里狀態方程，以及Murnaghan狀態方程等。EXPLO-5的現行版本由于應用JCZ3 EOS方程，爆炸參數的預測準確性得到提高。EXPLO-5的數據庫目前包含260種反應物，超過330種產物(包括同一產物的不同相態)，并包含了32種元素：C, H, N, O, Al, Cl, Si, F, B, Ba, Ca, Na, P, Li, K, S, Mg, Mn, Zr, Mo, Cu, Fe, Ni, Pb, Sb, Hg, Be, Ti, I, Xe, U,和W。

除EXPLO-5外，波蘭華沙技術大學最近也開發了一款名為ZMWNI的熱力學軟件。它可以計算含能材料的燃燒、爆炸和熱力學參數，并確定爆轟產物的JWL等熵膨脹曲線[73]和爆轟能[74]等。此外，ZMWNI代碼能夠確定不同溫度下，配方在非平衡狀態的爆轟參數。程序基于最小化學勢法計算平衡或非平衡組分的反應性體系。最終數據采集是通過求解線性方程組和最陡降法獲得的[75]。氣體的物理性質則由BKW方程狀態描述。上述的TIGER和CHEETAH都采用凝聚相組分OLD狀態方程，用于計算給定條件下HEDM的燃燒或爆炸的平衡狀態和定容爆轟參數。ZMWNI熱力學軟件則不需要給定條件，可以計算非理想狀態下的任何參數。總之，在熱力學計算領域，我國的發展水平相對落后，這在一定程度上制約我國新型含能材料的理論設計、開發和應用。

4 含能材料反應活性的分子動力學模擬

原子級別的模擬方法有：分子動力學(MD)和蒙特卡諾(MC)模擬。它們考慮單個原子或官能團，可以預測含能材料晶體、晶體與黏合劑之間界面的動態性能。分子動力學模擬中原子間作用力可以通過經驗力場參數來計算，而力場又是基于電子結構和體系瞬態電子的波函數。其中分子動力學模擬能量場中的擴散比較有效。目前主要商業軟件包括美國的Material Studio和荷蘭的ADF軟件(后面提到的反應力場ReaxFF模塊也已經嵌入該軟件)。分子間相互作用遵循一定的近似物理規律，在原子水平上有一定的復雜性。因此，“力場”被用來模擬結構、振動、構象和熱物理特性。含能材料研究中常用的力場是“簡明相優化分子勢原子力場”(COMPASS)。 COMPASS力場可準確地模擬孤立分子和固相材料分子的性能。分子模型COMPASS力場可以克服現實實驗中遇到的困難，已成功用于模擬增塑劑擴散性以及它們與HTPB推進劑黏結體系的相容性[76]。COMPASS力場還被用來模擬HTPB對Al、氧化鋁吸附能和它們之間的界面力學性能(如彈性系數、模量和泊松比等)。通過分析吸附能量和相關函數，可以模擬界面相互作用的性質。在涉及建模和仿真熱力學領域，國內已開展了一定的工作。蕭忠良等[77]完成了一些發射藥氣體體積流量、氧平衡和能量釋放量的建模。

含能材料分子動力學研究的熱點還包括采用ReaxFF來模擬含能材料的熱分解和燃燒過程[78]。ReaxFF基于從頭量子力學(QM)計算，可準確描述烴和各種CHNO體系的反應性，如RDX同系物的分解途徑及后續氣相化學反應[79-80]。在模擬高能材料分解的化學途徑方面，“HE”力場是專門為硝銨化合物構建的[81-82]。在“HE”力場基礎上發展了另一個普適于含能化合物的力場“CHONSSi-lg”，該力場考慮了倫敦色散力的影響[83]，但它不包含氟原子的數據。為了更好地比較含氟配方(如含氟聚物)，可采用“TiOCHNCl”力場[84]。除ReaxFF可以模擬計算含能材料化學反應機理之外，還可采用CFD軟件進行建模計算。如北京化工大學開發了基于渦級聯和分形理論的現象學概念來模擬湍流化學反應的分形模型(FM)，采用湍流燃燒化學反應和渦耗散概念(EDC)模型，可以模擬含能材料燃燒反應機理[85]。王國青等[86]使用DFT和高斯03軟件，研究了TNT與硫酸根的反應機理。在他們的研究中，所有反應物分子、過渡態結構和產物均在B3LYP/6-31G(d)水平下進行了幾何優化。除了研究反應機理，數值建模和仿真也被用于反應動力學研究。如機械損傷對PBX起爆和爆轟行為的影響。該反應模型可以分析含缺陷的炸藥爆轟機制，其孔隙率和粒徑隨沖擊載荷而改變[87]。建模和仿真還可以用于模擬推進劑的燃燒。如封鋒等[88]開發的SPRS軟件可以計算推進劑的化學成分及其在指定壓力下的燃速和壓力指數。固體推進劑的組分可以根據所需的燃燒速率和壓力指數來確定。此數值模擬縮短固體推進劑的研發周期，進而節約成本。發射藥方面，張江波等[89]開發了基于經典內彈道理論產生的多層推進劑裝藥內彈道數學模型模擬程序。發射藥和推進劑數值模擬研究包括以下幾個方面：(1)由于對發射藥的發射負荷引起的內孔變形；(2)變燃速發射藥的逐層可燃性；(3)環境溫度、組分、粒徑和硼粉氧化膜厚度對點火性能的影響；(4)硼粉團聚對富燃料固體推進劑能量釋放速率和燃速性能的影響。此外，蕭忠良等[90]發展了推進劑定容燃燒行為的數學模型，并在此基礎上研究了腹板厚度和非同步點火對推進劑燃速系數的影響。數值建模和仿真還可用于某些特殊研究領域。如使用熱機械耦合有限元法研究在固體推進劑整形加工過程的危險性。采用基于黏彈性積分本構關系的方法，確定了由整形過程中壓力和摩擦產生的熱量，并且對危險點進行計算。數值模擬的另一種應用是基于固化時間理論的修正蠕變模型，該模型用以模擬塑料黏結炸藥(PBX)組分短時間內的蠕變行為。該模型還被用來模擬HMX-PBX炸藥在受真空吸力過程中的緩慢蠕變行為。數值模擬和理論分析表明，改進的固化時間蠕變模型適用于模擬PBX瞬時蠕變行為。

5 結束語

含能材料的發展日臻完善，主要研究領域包括含能化合物的分子設計、含能材料納米化、共晶化與表面改性、含能材料分解點火燃燒與爆轟、極限條件下含能材料的響應、含能材料配方設計及工程化應用、含能材料安全性能與綠色利用，及含能材料的量化計算與多尺度分子模擬等。對于含能材料的物理化學性能預估，可以采用量子化學、分子動力學或滿足半經驗QSPR模型的方法來預估含能材料的感度、燃燒性能、爆轟性能、反應活性、固化機制與力學性能等。目前存在的主要發展瓶頸有：

(1)沒有建立統一標準的含能材料性能實驗數據庫，無法滿足匹配大量模擬和模型訓練的需求。且諸多數據的測試標準不統一，人為因素影響了結果的可靠性；

(2)建模和參數有待進一步系統化和標準化，國內未能創立商業化計算軟件，且對國外相關商業化軟件的二次開發較少。有待于進一步加大模擬仿真方面的投入力度，確保建立更加精確、可靠，普適性強的預測模型；

(3)目前商業軟件僅局限于預測含能材料的爆轟性能和燃燒性能，對于安全性能的理論計算還處于探索階段。有待以建模仿真和量子化學計算為基礎創立一個能評價含能材料理化與安全性能的綜合體系。

[1] Short J M,Kavetsky R A, Davinder K.Energetics Science and Technology in Central Europe [M].Maryland:CALCEEPSC Press,2013.

[2] 王睿, 蔣軍成, 潘勇, 硝基含能材料撞擊感度的預測研究進展[J], 工業安全與環保, 2010, 36(7):19-22.

WANG Rui, JIANG Jun-cheng, PAN Yang. Research on the prediction of impact sensitivity of nitro energetic materials [J]. Industrial Safety and Environment Protection, 2010, 36(7):19-22.

[3] 王澤山.含能材料概論 [M]. 哈爾濱: 哈爾濱工業大學出版社, 2006.

[4] 董海山. 評介《四唑化學的現代理論》[J]. 含能材料, 2002(2):95-96.

[5] Zeman S, Jungová M. Sensitivity and performance of energetic materials[J]. Propellants, Explosives, Pyrotechnics,2016,41:426-451.

[6] 房偉, 王建華, 劉玉存,等. 基于分子基團預測硝基含能材料撞擊感度[J].火工品, 2014(5):34-37.

FANG Wei, WANG Jian-hua, LIU Yu-cun, et al.Prediction on impact sensitivity of nitro-energetic materials by molecular groups [J]. Initiators & Pyrotechnics,2014(5):34-37.

[7] 劉歡, 姜峰, 于國強,等.遺傳-神經網絡方法在炸藥撞擊感度預測中的應用研究[J], 火工品, 2010(6):42-45.

LIU Huan, JIANG Feng, YU Guo-qiang,et al. Application research of genetic-neural network method in the prediction of explosives′ impact sensitivity [J].Initiators & Pyrotechnics, 2010(6):42-45.

[8] 王睿, 蔣軍成, 潘勇,等. 均三硝基苯類化合物撞擊感度與電性拓撲指數的QSPR研究[J].含能材料, 2008, 16(1):90-93.

WANG Rui, JIANG Jun-cheng, PAN Yong, et al. QSPR study of correlation between impact sensitivity of m-nitroaromatics and electrotopological state indices [J]. Chinese Journal of Energetic Materials, 2008, 16(1):90-93.

[9] 肖鶴鳴.四唑化學的現代理論 [M].北京：科學出版社, 2000.

[10] 肖鶴鳴, 朱衛華, 肖繼軍,等.含能材料感度判別理論研究——從分子、晶體到復合材料[J].含能材料, 2012, 20(5):514-527.

XIAO He-ming, ZHU Wei-hua, XIAO Ji-jun. et al. Theoretical studies on sensitivity criterion of energetic materials-from molecules, crystals, to composite materials[J]. Chinese Journal of Energetic Materials, 2012, 20(5):514-527.

[11] Nefati H,Cense J M, Legendre J J. Prediction of the impact sensitivity by neural networks [J].Journal of Chemistry Information Computer Science, 1996, 36: 804.

[12] Smirnov A, Voronko O, Korsunsky B, et al. Impact and friction sensitivity of energetic materials:methodical evaluation of technological safety features [J]. Chinese Journal of Explosives and Propellants, 2015, 38 (3): 1-8.

[13] 金韶華, 王偉, 松全才. 含能材料機械撞擊感度判據的認識和發展 [J]. 爆破器材, 2006, 35(6):11-14.

JIN Shao-hua, WANG Wei, SONG Quan-cai, Understanding and development of criteria of impact sensitivity of energetic materials [J]. Explosive Materials, 2006, 35(6):11-14.

[14] 李金山, 曹剛, 肖鶴鳴, 等. 多硝基芳香化合物撞擊感度的量子化學研究 [J]. 火炸藥學報, 1997,20(2):57-58.

LI Jin-shan, CAO Gang, XIAO He-ming,et al. Quantum chemical study on the impact sensitivity of polynitroaromatics[J].Chinese Journal of Explosives & Propellants(Huozhayao Xuebao), 1997,20(2):57-58.

[15] Bowden F, Yoffe Y. Initiation and Growth of explosion in Liquids and Solids [M].London:Cambridge University Press, 1952.

[16] Delpuech A, Cherville J, Michaud C. Molecular electronic structure and initiation of secondary explosives[C]∥7th Symposium (International) on Detonation. Annapolis:[s.n.],1981.

[17] Kamlet M J, Adolph H G. The relationship of impact sensitivity with structure of organic high explosices [J]. Propellants, Explosives, Pyrotechnics, 1979, 4: 30.

[18] Chen Z X, Xiao H M. Quantum chemistry derived criteria for impact sensitivity [J].Propellants, Explosives, Pyrotechnics, 2014, 39 (4):487-495.

[19] Murray J S, Lane P, Politzer P.Relationships between impact sensitivities and molecular surface electrostatic potentials of nitroaromatic and nitroheterocyclic molecules [J]. Molecular Physics, 1995, 85 (1): 1-8.

[20] Politzer P, Murray J S. Impact sensitivity and crystal lattice compressibility/free space [J].Journal of Molecular Modeling, 2014,20(5):2223.

[21] Keshavarz M H. Calculations of bond dissociation energies and dipole moments in energetic materials using density-functional methods [J]. Journal of Hazardous Material, 2007, 148: 658-662.

[22] Keshavarz M H, Motamedoshariati H,Pouretedal H R,et al. Prediction of shock sensitivity of explosives based on small-scale gap test [J]. Journal of Hazardous Material, 2007, 145: 109-112.

[23] Keshavarz M H, Shokrolahi A, Esmailpoor K,et al, Prediction of heats of sublimation of energetic compounds using their molecular structures [J].Energetic Materials, 2008, 177(1-3):648-659.

[24] Liu X, Su Z, Ji W,et al. Structure, physicochemical properties, and density functional theory calculation of high-energy-density materials constructed with intermolecular interaction: nitro group charge determines sensitivity [J]. Journal of Physical Chemistry C, 2014, 118 (41):23487-23498.

[25] Mullay J. A relationship between impact sensitivity and molecular electronegativity [J]. Propellants, Explosives, Pyrotechnics, 1987, 12 (2): 60-63.

[26] Ren F D, Cao D L, Shi W J,et al. A theoretical prediction of the relationships between the impact sensitivity and electrostatic potential in strained cyclic explosive and application to H-bonded complex of nitrocyclohydrocarbon [J].Journal of Molecular Modeling, 2016, 22(4).

[27] Rice B M, Hare J J, Phys J.A quantum mechanical investigation of the relation between impact sensitivity and the charge distribution in energetic molecules[J].Journal of Physical Chemistry Chem A,2002, 106, 1770-1783.

[28] Politzer P, Murray J S. Impact sensitivity and the maximum heat of detonation[J]. Journal of Molecular Modelling, 2015, 21 (10):262:11.

[29] Zohari N, Keshavarz M H, Seyedsadjadi S A A link between impact sensitivity of energetic compounds and their activation energies of thermal decomposition [J]. J Therm Anal Calorim, 117(1):423-432.

[30] Mathieu D, Alaime T. Predicting impact sensitivities of nitro compounds on the basis of a semi-empirical rate constant [J]. Journal of Physical Chemistry A, 2014, 118 (41):9720-9726.

[31] Tan B S, Huang M, Li J S,et al. A new sensitivity criterion of explosives: bonding & nonbonding coupling related molecular rigidity and flexibility [J]. Chinese Journal of Energetic Materials, 2016,24 (1):10-18.

[32] Keshavarz M H, Motamedoshariati H, Moghayadnia R,et al. Prediction of sensitivity of energetic compounds with a new computer code [J]. Propellants, Explosives, Pyrotechnics, 2014, 39(1): 95-101.

[33] Mullay J. Relationships between impact sensitivity and molecular electronic structure [J]. Propellants, Explosives, Pyrotechnics, 1987, 12 (4): 121-124.

[34] Edwards J, Eybl C, Johnson B. Correlation between sensitivity and approximated heats of detonation of several nitroamines using quantum mechanical methods [J]. International Journal of Quantum Chemistry, 2004,100 (5):713-719.

[35] 曹霞, 向斌, 張朝陽. 炸藥分子和晶體結構與其感度的關系[J]. 含能材料, 2012(5): 643-649.

CAO Xia, XIANG Bin, ZHANG Chao-yang. Review on relationships between the molcular and crystal structure of explosives and their sensitivities [J]. Chinese Journal of Energetic Materials, 2012(5): 643-649.

[36] Nefati H, Cense J M, Legendre J J. Prediction of the impact sensitivity by neural networks[J]. Journal of Chemical Information and Computer Sciences, 1996, 36 (4): 804-810.

[37] Cho S G., No K T , Goh E M, et al. Optimization of neural networks architecture for impact sensitivity of energetic molecules[J]. Bulletin of the Korean Chemical Society, 2005, 26 (3):399-408.

[38] Wang R, Jiang J, Pan Y. Prediction of impact sensitivity of nonheterocyclic nitroenergetic compounds using genetic algorithm and artificial neural network [J]. Journal of Energetic Materials, 2012,30 (2):135-155.

[39] Keshavarz M H, Jaafari M. Investigation of the various structure parameters for predicting impact sensitivity of energetic molecules via artificial neural network[J]. Propellants, Explosives, Pyrotechnics, 2006, 31 (3):216-225.

[40] 王睿, 蔣軍成, 潘勇, 等. 均三硝基苯類化合物撞擊感度與電性拓撲態指數的QSPR的研究[J]. 含能材料, 2008, 16(1): 90-93.

WANG Rui, JIANG Jun-cheng,PAN Yong, et al. QSPR study of correlation between impact sensitivity ofm-nitroaromatics and electrotopological state indices[J].Chinese Journal of Energetic Materials,2008,16(1):90-93.

[41] 王睿, 蔣軍成, 潘勇, 等. 電性拓撲態指數預測硝基類含能材料撞擊感度[J].固體火箭技術, 2008, 31(6): 647-662.

WANG Rui, JIANG Jun-cheng,PAN Yong, et al. Predicton on impact sensitivity of nitro energetic materials by means of electrotopological state indices[J]. Journal of Solid Rocket Technology,2008,31(6):647-662.

[42] Jason A Morrill,Edward F C Byrd.Development of quantitative structure-property relationships for predictive modeling and design of energetic materials[J].Journal of Molecular Graphics and Modeling,2008,27(3):349-355.

[43] 肖鶴鳴, 王遵堯, 姚劍敏. 芳香族硝基炸藥感度和安定性的量子化學研究-I. 苯胺類硝基衍生物[J].化學學報, 1985, 43 (1): 14-18.

XIAO He-ming,WANG Zun-yao,YAO Jian-min. Quantum chemical study on sensitivity and stability of aromatic nitro explosives i. nitro derivatives of aminobenzenes[J]. Acta Chimica Sinica,1985,43(1):14-18.

[44] Kim C K, Cho S G, Li J, et al. QSPR studies on impact sensitivities of high energy density molecules [J]. Bulletin Korean Chemical Society, 2011, 32(12):4341-46.

[45] Keshavarz M H, Keshavarz Z. Relation between electric spark sensitivity and impact sensitivity of nitroaromatic energetic compounds [J]. Zeitschrift fur Anorganische and Allgemeine Chemie, 2016, 642 (4):335-342.

[46] Cazamias J U, Schraml S J. Modeling of non-eroding penetration using ALE3D and Zapotec [C]∥ AIP Conference Proceedings. [S.l.]:Inverse Problems International Association, 2007, 955:1281-1284.

[47] Pierce T, Rodrigue G. A parallel two-sided contact algorithm in ALE3D [J]. Computer Methods in Applied Mechanics and Engineering, 2005,194 (27-29):3127-3146.

[48] McClelland M A, Maienschein J L, Howard W M, et al. ALE3D simulation of heating and violence in a fast cookoff experiment with LX-10 [C]∥ Proceedings of the 13th International Detonation Symposium.[S.l.]:Office of Naval Research,2006:606-616.

[49] Kuo I W, Bastea S, Fried L E. Reactive flow modeling of liquid explosives via ale3d/cheetah simulations [C]∥ Proceedings of 14th International Detonation Symposium. [S.l.]:Office of Naval Research, 2010:333-337.

[50] O′Daniel J L. Modeling contact detonations with ALE3D and PARADYN [J]. Computational Fluid and Solid Mechanics ,2003:537-539.

[51] Howard W M, McClelland M A, Knap J, et al. Ale3d simulations of gap closure and surface ignition for cookoff modeling [C]∥ Proceedings of the 13th International Detonation Symposium.[S.l.]:Office of Naval Research,2006: 1247-1255.

[52] Knap J, McClelland M A, Maienschein J L, et al. Measurement and ale3d simulation of violence in a deflagration experiment with lx-10 and aermet-100 alloy [C]∥Proceedings of the 13th International Detonation Symposium.[S.l.]:Office of Naval Research,2006:662-671.

[53] Stewart J J P. MOPAC: A semiempirical molecular orbital program [J]. Journal of Computer-Aided Molecular Design, 1990, 4(1): 1-103.

[54] Gicquel L Y M, Staffelbach G, Poinsot T. Large Eddy Simulations of gaseous flames in gas turbine combustion chambers[J]. Progress in Energy and Combustion Science,2012, 38 (6): 782-817.

[55] Beckstead M W, Liang Y, Pudduppakkam K V. Numerical simulation of single aluminum particle combustion [J]. Combustion, Explosion and Shock Waves, 2005, 41 (6): 622-638.

[56] Ermolin N E, Zarko V E. Simulation of combustion of cyclic nitramines [J].Fizika Goreniya i Vzryva, 1998, 34 (5): 3-22.

[57] Wang J, Wight C A. Use of kinetic models for solid state reactions in combustion simulations [J]. Theoretical Computational Chemistry, 2003,13: 351-371.

[58] Stewart J J P. MOPAC: A semiempirical molecular orbital program [J]. J Computer-Aided Mol Des, 1990, 4(1): 1-103.

[59] Bredow T, Jug K. Theory and range of modern semiempirical molecular orbital methods[J]. Theoretical Chemistry Accounts, 2005, 113(1):1-14.

[60] Repasky M P, Chandrasekhar J, Jorgensen W L. PDDG/PM3 and PDDG/MNDO: improved semiempirical methods [J]. Journal of Computational Chemistry, 2002, 23: 1601-1622.

[61] Dorsett H, White A. Overview of molecular modelling and Ab initio molecular orbital methods suitable for use with energetic materials[R].Salisbury: DSTO Aeronautical and Maritime Research Laboratory， 2000.

[62] 舒遠杰. 含能材料的理論研究與數值模擬進展 [M]. 綿陽：中國工程物理研究院科技年報(2009年版) , 2010： 115-117.

[63] Byrd E F C，Rice B M. Improved prediction of heats of formation of energetic materials using quantum mechanical calculations [J]. Journal of Physical Chemistry A,2006, 110(3): 1005-1013.

[64] Mohammad H K. Improved prediction of heats of sublimation of energetic compounds using their molecular structure[J]. Journal of Hazardous Materials, 2010, 177(1-3): 648-659.

[65] Politzer P, Murray J S. The fundamental nature and role of the electrostatic potential in atoms and molecules[J]. THEO CHEM ACCS, 2002, 108(3):134-142.

[66] Mathieu D. Simple alternative to neural networks for predicting sublimation enthalpies from fragment contributions[J]. Ind Eng Chem Res, 2012, 51(6):2814-2819.

[67] Farhad Gharagheizi, Mehdi Sattari, Behnam Tirandazi. Prediction of crystal lattice energy using enthalpy of sublimation: a group contribution-based model[J]. Ind Eng Chem Res, 2011, 50:2482-2486.

[68] Kamlet M J, Jacobs S J. Chemistry of detonations. I. A simple method for calculating detonation properties of C-H-N-O explosives[J]. Journal of Chemical Physics, 1968, 48:23-35.

[69] 邱玲. 氮雜環硝胺類高能量密度材料(HEDM)的分子設計[D]. 南京：南京理工大學, 2007.

[70] Persson P A. TIGER WIN—a window PC code for computing explosive performance and thermodynamic properties [C]∥ Proceedings of 2000 High-tech Seminar, State-of-the Art Blasting Technology and Explosive Applications. Orlando:[s.n.],2000:541.

[71] Grys S, Trzciński W A.Characteristics of Energetic Materials[J].Central European Journal of Energetic Materials,2010,7(2):97-113.

[72] Lu J P. Evaluation of the Thermochemical Code - CHEETAH 2.0 for Modelling Explosives Performance, DSTO-TR-1199[R]. Australia:DSTO,2001:1-34.

[73] Lee E L, Horning H C, Kury J W. Adiabatic expansion of high explosive detonation products,UCRL-50422[R]. Livermore : Lawrence Livermore National Laboratory, 1968.

[74] Jacobs S J. Energy of detonation, NAVORD-4366[R].[S.l.]: Naval Ordnance Laboratory, 1956.

[75] White W B, Johnson S M, Danzig G B. Chemical equilibrium in complex mixtures [J].J Chem Phys,1958, 28: 751-755.

[76] Li H X, Qiang H F, Wu W M. Molecular simulation on plasticizer migration in the bond system of HTPB propellant [J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao), 2008, 31(5):74-78.

[77] 代淑蘭,許厚謙,肖忠良,等. 帶制退器的膛口燃燒流場并行數值模擬 [J]. 彈道學報, 2009,21(4):84-87.

DAI Shu-lan, XU Hou-qian, XIAO Zhong-liang. Numerical simulation of muzzle combustion flow field with brake by parallel computation [J]. Journal of Ballistics, 2009,21(4):84-87.

[78] Duin van A C T, Dasgupta S, Lorant F, et al. A reactive force field for hydrocarbons [J]. Journal of Physical Chemistry A, 2001, 105 (41):9396-9409.

[79] Strachan A, van Duin A C T, Chakraborty D, et al. Shock waves in high-energy materials: the initial chemical events in nitramine RDX [J]. Physical Reveiw Letter, 2003, 91: 098301.

[80] Strachan A, Kober E.M, van Duin Adri C T, et al. Reactive molecular dynamics [J]. Journal of Physical Chemistry, 2005, 122:054502.

[81] Li Z, Lang C, Chen W, et al. Molecular dynamics study of the effect of H2O on the thermal decomposition of α-phase CL-20 [J]. Acta Physial Chimica Sinica, 2013, 29(6):1145-1153.

[82] Zhang L, Zybin S, van Duin A C T, et al. Carbon cluster formation during thermal decomposition of octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine and 1,3,5-Triamino-2,4,6- trinitrobenzene high explosives from ReaxFF reactive molecular dynamics simulations [J]. Journal of Physical Chemistry A, 2009, 113: 10619-10640.

[83] Liu L, Liu Y, Zybin S V, et al. Correction of the ReaxFF reactive force field for London Dispersion, with applications to the equations of state for energetic materials [J]. Journal of Physical Chemistry A, 2011, 115 (40): 11016-11022.

[84] Chenoweth K, Cheung S, van Duin A C T, et al. Simulations on the thermal decomposition of a poly(dimethylsiloxane) polymer using the ReaxFF reactive force field [J]. J Am Chem Soc, 2005, 127 (19): 7192-7202.

[85] 張建文，王艷飛, 湍流化學反應的分形數值模擬[J]. 火炸藥學報, 2007, 30(3): 5-8, 15.

ZHANG Jian-wen., WANG Yan-fei. Numerical simulation for turbulent chemical reaction [J]. Chinese Journal Explosives & Propellants(Huozhayao Xuebao), 2007, 30(3):5-8, 15.

[86] 王國青,吳玉凱,侯慶偉,等.硫酸自由基與TNT反應的密度泛函理論[J]. 火炸藥學報, 2010, 33(2):10-12, 18.

WANG Guo-qing, WU Yu-kai, HOU Qing-wei, et al. A density functional theory of the reaction of TNT with sulfate radical [J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao), 2010, 33(2):10-12, 18.

[87] 梁增友,黃風雷,張振宇,等. PBX炸藥二維沖擊起爆機理的數值模擬[J]. 火炸藥學報, 2008, 31(5):15-18.

LIAGN Zeng-you, HUANG Feng-lei, ZHANG Zhen-yu, et al. Numerical simulation of two dimension shock initiation and detonation behavior of PBX [J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao), 2008, 31(5):15-18.

[88] 封鋒, 陳軍, 鄭亞,等.基于一維氣相穩態反應流的燃速預估軟件研究[J]. 火炸藥學報, 2009, 32(3):58-61, 65.

FENG Feng, CHEN Jun, ZHENG Ya, et al. Study on software of solid propellant burning rate prediction based on one-dimensional steady-state reaction gas flow [J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao),2009, 32(3):58-61, 65.

[89] 張江波,張玉成,蔣樹君,等.多層發射藥內彈道模型及數值求解[J]. 火炸藥學報, 2009, 32(3):83-86.

ZHAGN Jiang-bo, ZHANG Yu-cheng, JIANG Shu-jun,et al. The interior ballistic model and numerical simulation of multilayer gun propellant charge [J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao), 2009, 32(3):83-86.

[90] 呂秉峰，劉幼平，董鳳云,等.定容條件下火藥實際燃燒規律的數值模擬[J]. 火炸藥學報, 2007, 30(6):72-74.

Lü Bing-feng, LIU You-ping, DONG Feng-yun, et al. The mathematical model of propellant actual combustion law on the constant volume condition[J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao), 2007, 30(6):72-74.

Research Progress in Theoretical Prediction of Physicochemical Properties for Energetic Materials

YAN Qi-long, SONG Zhen-wei, AN Ting, ZHANG Xiao-hong, ZHAO Feng-qi

(Science and Technology on Combustion and Explosion Laboratory, Xi′an Modern Chemistry Research Institute,Xi′an 710065, China)

Starting from the related achievements of recent development in the field of energetic materials, the main research direction in this field was discussed, and the latest achievements of theoretical prediction of the physicochemical properties of energetic materials were described in particular, mainly including quantum chemistry, molecular dynamics or semi empirical QSPR modeling approaches to predict the research progress in sensitivity, combustion and detonation performances, reaction activity, curing mechanism and mechanical properties of energetic materials.The main technical barriers existed at present were summarized, including the lack of complete and unified standard experimental database on performances of energetic materials, no commercial software with independent intellectual property rights to calculate the energetic material properties, and international commercial software with reliable predictors of physical and chemical properties of energetic materials is limited to the detonation performance and combustion performance. Literature research shows that China needs to further strengthen the research in this field, and finally build a comprehensive software platform that can evaluate the performance and security of energetic materials.With 90

.

10.14077/j.issn.1007-7812.2016.05.001

國家自然科學基金(No.21303133;No.21473130)

嚴啟龍(1983-)，男，博士，高級工程師，從事含能材料性能及表征研究。E-mail:terry.well@163.com

趙鳳起(1963-)，男，博士，博士生導師，研究員，從事固體推進劑配方與性能研究。E-mail:zhaofqi@163.com

TJ55；TQ560

A

1007-7812(2016)05-0001-12