基于遺傳算法的二次回歸方程在沉降數據處理中的應用

王江榮，趙　睿，袁維紅，任泰明

（1.蘭州石化職業技術學院 信息處理與控制工程系，甘肅 蘭州730060；2.蘭州石化職業技術學院 土木工程系，甘肅 蘭州730060）

基于遺傳算法的二次回歸方程在沉降數據處理中的應用

王江榮1，趙睿1，袁維紅2，任泰明1

（1.蘭州石化職業技術學院 信息處理與控制工程系，甘肅 蘭州730060；2.蘭州石化職業技術學院 土木工程系，甘肅 蘭州730060）

軟基路基沉降與其影響因素之間呈非線性關系。以某軟基高速公路為例，以時段天數、時段載荷量及時段加載平均速率為解釋變量，以時段沉降量為被解釋變量，建立了非線性二次回歸模型，并用遺傳算法估算模型系數。工程實例表明，經遺傳算法優化的非線性二次回歸方程具有較高的預測精度，效果優于神經網絡，用該模型進行軟基高速公路沉降預測分析是可行的。

路基沉降；二次回歸方程；神經網絡；遺傳算法；預測分析

0　引言

在軟土地基上修建高速公路面臨的主要問題是如何有效控制路基沉降。由于軟土地質堅固性低、壓縮性大、透水性差，一旦發生變形，往往持續時間較長，這些特點給高速公路建設造成一定困難。較為準確地預測軟基沉降是保證施工質量、有效控制沉降變形的關鍵。尋求可操作性強、精確度高、有較強數據適應能力的沉降預測方法是工程技術人員長期的追求。因為軟土路基沉降是一個復雜的非線性系統，其影響因素較多[1-3]，其中可量化、易于采集且對路基沉降有重要影響的因素有填土時間、載荷量及加載速率等。對于這類多因素非線性系統的數據處理許多研究者采用了人工神經網絡方法[4-7]，并取得了不錯的效果。但人工神經網絡存在模型結構復雜、運算量大、運算結果不穩定和預測精度不高的問題。另外，神經網絡對樣本數據的數量及質量要求較高，且容易發生過擬合現象?；诖?，本文給出另一種沉降數據處理方法——二次回歸分析法，并對其中的模型參數采用遺傳算法求解。工程實例分析表明，基于遺傳算法的二次回歸方程具有較高的精確度和可靠性，沉降預測效果優于神經網絡，而且模型結構簡單、變量間的依賴關系清晰、實際操作方便，用以軟基路基沉降預測是可行的。

1　基礎數據

文獻 [8]介紹了某軟基高速公路的工程概況（在此略去）,并以時段沉降量為目標觀測值y （mm)，以時段天數t（d)、時段載荷量[時段填土高度P(m)]和時段填土速率ΔP(m/d)為指標觀測值（屬性值），經過約13個月觀測得到了25組觀測數據，見表1。

以表1中序號1～20的數據建模，并用序號21～25的數據檢測模型。

2　模型建立

設x1=時段天數（d），x2=時段填土高度（m),x3=時段填土速率（m/d）,y=時段沉降量（mm）。則y關于x1、x2及x3的完全二次回歸方程為

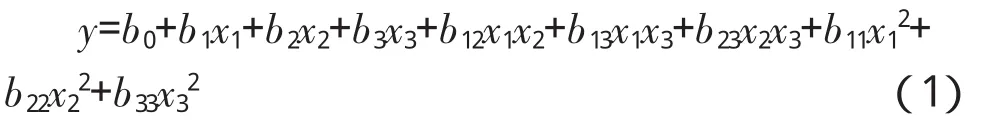
式中：b0、b1、b2、b3、b12、b13、b23、b11、b22、b33為回歸系數。采用遺傳算法來估算這些回歸系數。

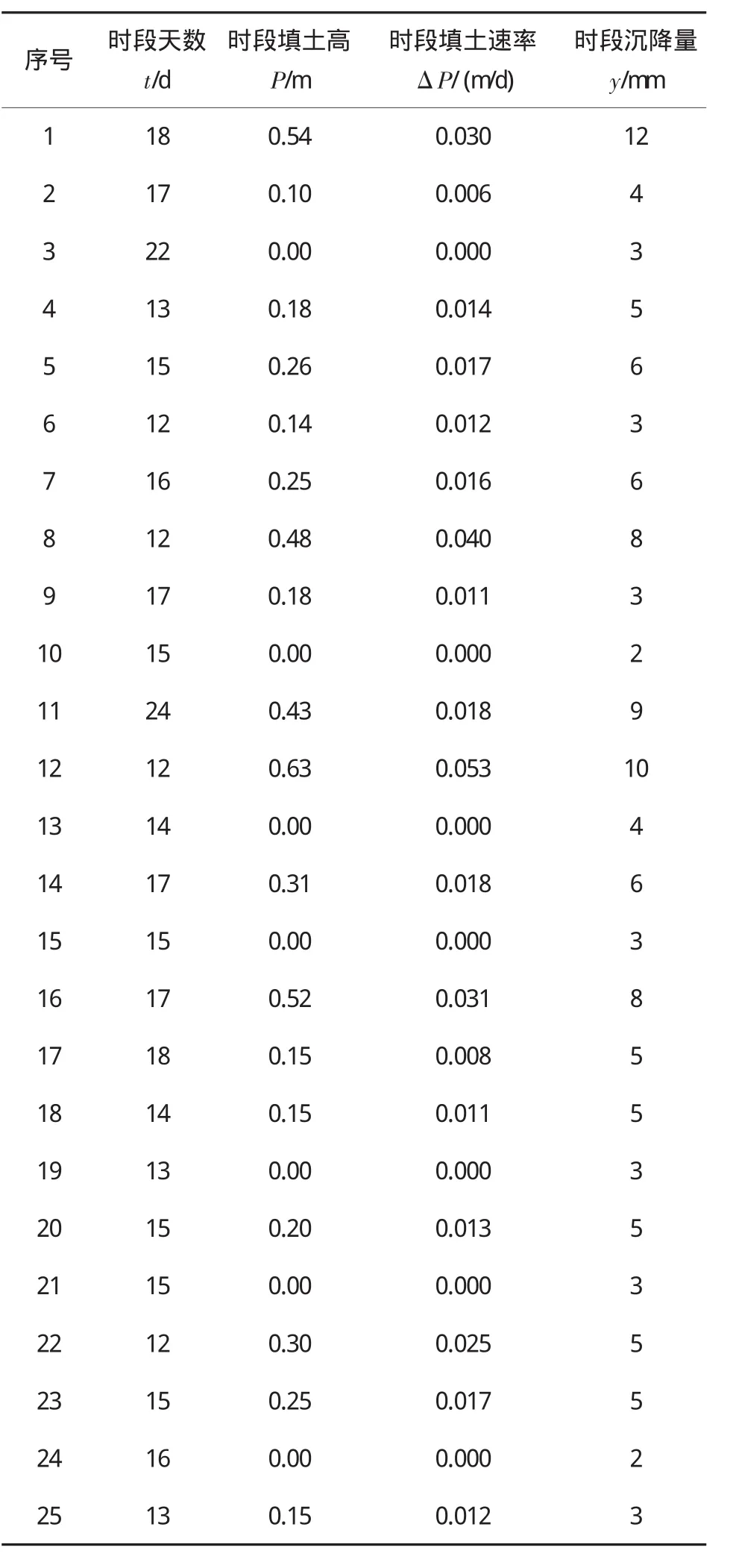
表1　沉降觀測數據表

在MATLAB工作窗口利用gatool命令打開遺傳算法的GUI[9],在Fitness function窗口輸入@finess，在Number of variables窗口輸入待估參數個數10，在邊界約束Lower輸入[3.95,-5.71,329.66,-3452.68, -20.52,137.13,-24002.64,-4.98,822.78,170349.03], 在Upper輸入 [13.95,4.29,339.66,-3442.68,-10.52, 147.13,-23992.64,5.02,832.78,170359.03],種群規模為80，迭代次數為4 000，其他參數選用缺省值，然后單擊Start按鈕執行遺傳算法，得出的適應度函數的變化過程如圖1所示。

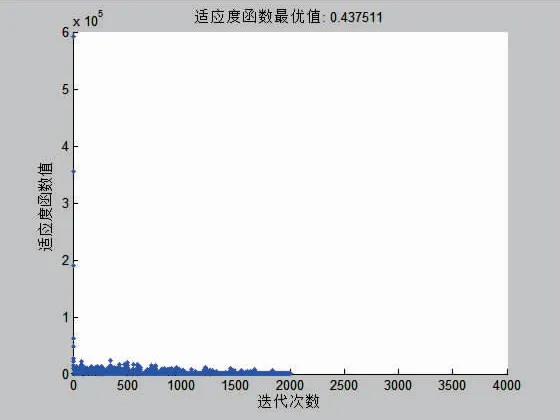
圖1適應度函數變化曲線

迭代2 000余次后終止，輸出的參數值（四舍五入）為：b0=3.949 6，b1=-0.028 2，b2=332.202 3，b3= -3 442.681 8，b12=-15.268 5，b13=139.491 3，b23=-23 992.643 9，b11=-0.002 3，b22=829.538 3，b33= 170 359.029 2。將這些參數值代入模型（1）得到的二次回歸方程為

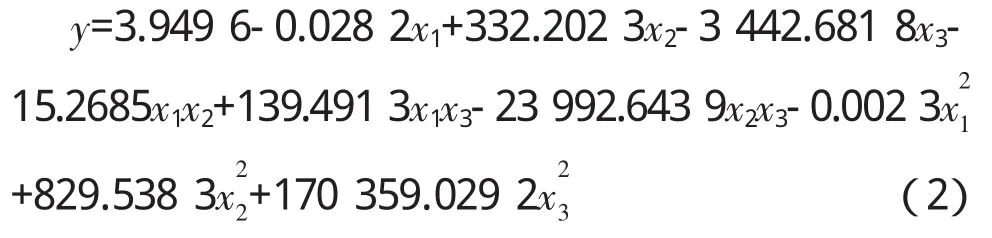
回歸方程的顯著性檢驗：決定系數R2=0.931 1,方均誤差MSE=0.437 5。可見回歸方程的擬合效果是顯著的，可以用于軟基路基沉降的后期預測。

3　模型檢驗

3.1模型預測精度分析

將測試樣本（表1中序號21～25的數據）的指標值即時段天數、時段填土高度和時段填土速率代入回歸方程（2）得出的時段沉降預測值見表2。作為比較，在相同樣建模樣本與測試樣本條件下，將文獻[8]中的神經網絡（網絡訓練樣本集由表1序號1～20數據構成，測試樣本為表1中序號21～25的數據）的預測結果和用逐步回歸法[確定方程（1）的模型系數，建模樣本為表1中序號1～20的數據，檢驗樣本為表1中序號21-25的數據]得出的預測結果置入表2中。

從表2給出的平均絕對誤差和平均相對誤差來看，本文建立的預測模型具有較高的精確度，預測結果整體好于文獻[8]給出的神經網絡的預測結果，也好于基于逐步回歸算法的二次回歸方程的預測結果。與神經網絡相比，本文模型最大的優點在于模型結構簡單，可操作性強，計算結果穩定，且對樣本數據無過多要求，用于指導高速公路建設是可行的。

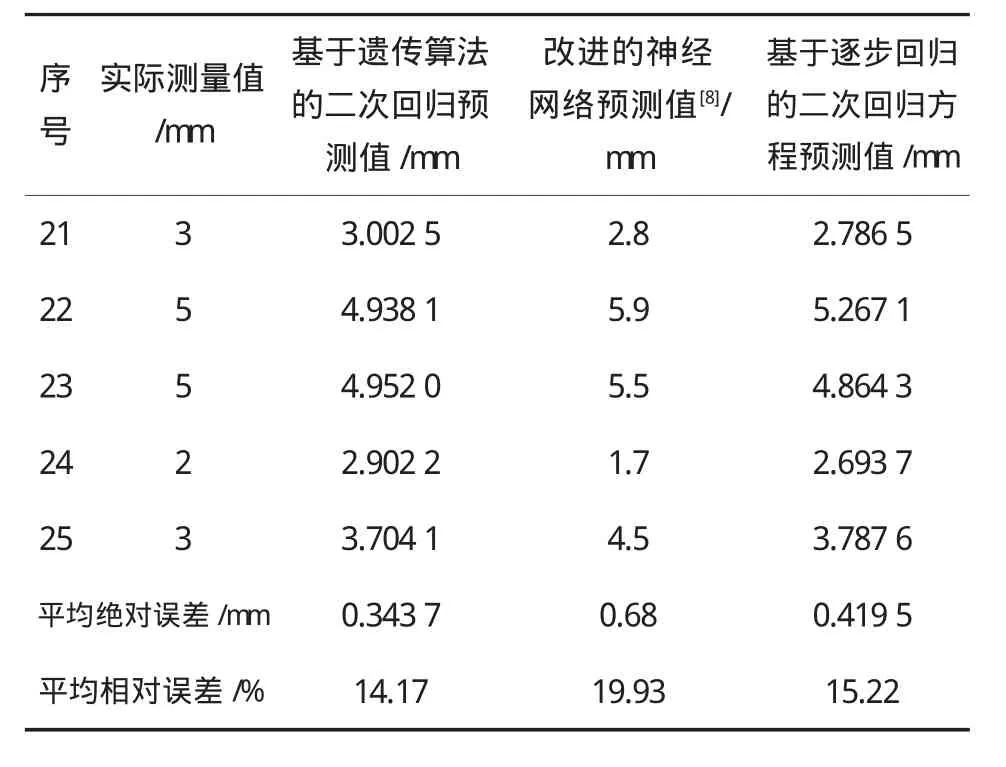
表2　測試數據的預測結果及分析比較

3.2模型可靠性分析

為了驗證模型的可靠性，將建模樣本數減少為15個，即利用表1中序號1～15的數據作為建模樣本，仍用序號21～25的數據來檢驗模型的預測精度。利用遺傳算法得出的模型系數和二次回歸方程為

測試樣本（表1中序號21～25的數據）的指標值即時段天數、時段填土高度和時段填土速率代入回歸方程（3）得出的時段沉降預測值見表3。

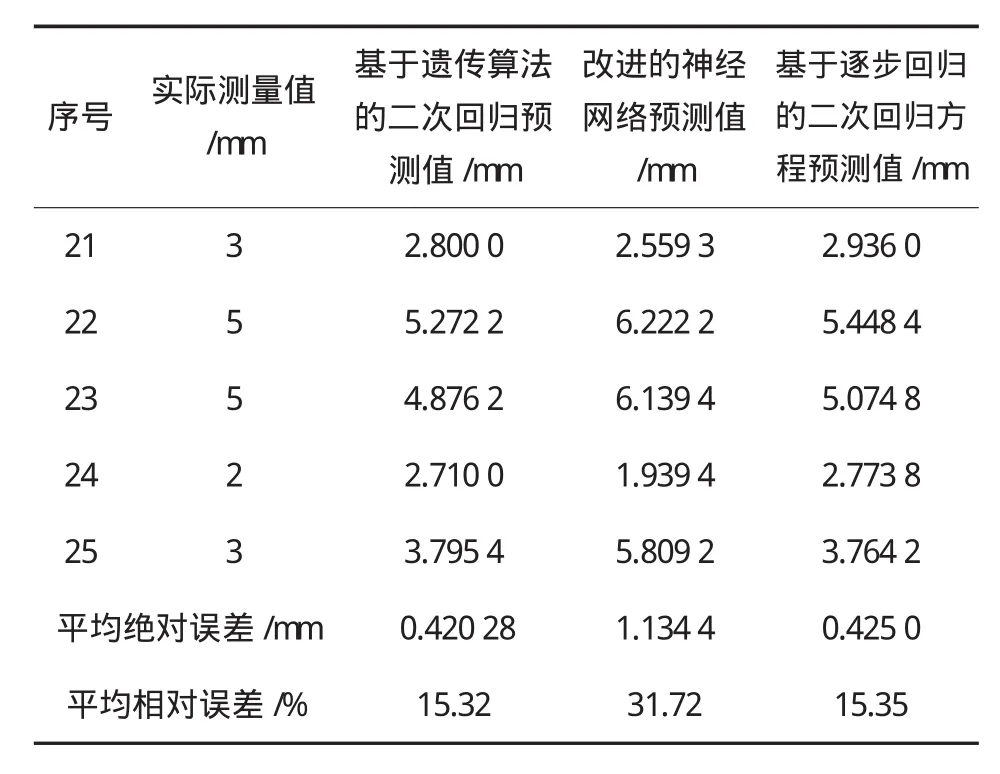
表3　基于15個建模樣本的三個模型的預測結果

從表3可看出，在減少建模樣本后三種模型的預測精度有不同程度的下降，尤其神經網絡的預測精度有了較大幅度的降低，已不能滿足工程需要；而本文模型及逐步回歸二次回歸方程的預測精度降幅很小，而以本文模型預測精度降幅最?。ǚ浅＝咏A測精度），能夠滿足工程需要。表明在減少建模樣本時本文模型的穩定性和可靠性較高，受其影響較小，而對神經網絡的預測精度影響較大。從另一方面說明神經網絡對建模樣本數量有較高的要求，只有訓練樣本數足夠多時才能取得理想的預測精度。

4　結語

軟基路基沉降與其影響因素(多因素）之間存在很強的非線性關系，神經網絡因其良好的非線性逼近能力被用以描述這種非線性關系。事實上神經網絡是一種非參數建模，解釋變量與被解釋變量之間的依賴關系不清晰，擬合預測值易受初始的影響，計算結果不穩定。

該文建立了基于遺傳算法優化的非線性二次回歸方程用以軟基路基沉降取得了理想效果，預測精度好于神經網絡，且具有較強的穩定性和可靠性。工程實例表明，利用非線性二次回歸方程模型進行沉降預測是可行的。這種精確模型（確定性模型）能否在多因素路基沉降預測問題上的適用性和通用性還需進一步論證。

[1]金雷.對高速公路軟土路基沉降影響因素分析[J].中國新技術新產品,2011(15):39.

[2]朱長青.高速公路軟土路基沉降影響因素探析[J].山東工業技術，2015（3）：118.

[3]劉光秀.軟土路基變形影響因素分析與沉降預測[D].秦皇島：燕山大學,2011.

[4]世強,梁武星,屈戰輝.BP神經網絡在預測路基沉降中的應用[J].西安工業大學學報,2006,26(5):452-456.

[5]孔繁盛，張彥拓.改進的 BP神經網絡在路基沉降預測中的運用[J].山西交通科技,2014(5):1-3,10.

[6]王新征,鄭偉花.人工神經網絡在預測軟基沉降中的應用研究[J].路基工程,2010(1):128-130.

[7]楊發群，邱衛寧，魏成,等.顧及不確定因素的GA－BP神經網絡在路基沉降預測中的應用[J].測繪工程,2013,22(6):51-54.

[8]胡伍生,方磊.動態預測軟土路基沉降的神經網絡模型研究[J].測繪科學,2008,33(6):110-112.

[9]許國根，賈瑛．模式識別與智能計算的MATLAB實現[M].北京:北京航空航天大學出版社，2012:182-183．

U41

A

1009-7716（2016）10-0149-03

10.16799/j.cnki.csdqyfh.2016.10.047

2016-05-11

蘭州市科學技術局計劃項目（蘭財建發〔2015〕85號）；蘭州石化職業技術學院科技資助項目（院發〔2015〕69號）；甘肅省科技廳計劃項目(1204GKCA004)；甘肅省財政廳專項資金立項資助（甘財教〔2013〕116號）

王江榮（1966-），男，甘肅靜寧人，碩士，教授，從

事路基沉降、控制理論與應用方面研究。