擴(kuò)展酉矩陣束算法實(shí)現(xiàn)稀疏可重構(gòu)天線陣的優(yōu)化設(shè)計

沈海鷗， 王布宏

空軍工程大學(xué) 信息與導(dǎo)航學(xué)院， 西安 710077

擴(kuò)展酉矩陣束算法實(shí)現(xiàn)稀疏可重構(gòu)天線陣的優(yōu)化設(shè)計

沈海鷗， 王布宏*

空軍工程大學(xué) 信息與導(dǎo)航學(xué)院， 西安 710077

針對方向圖可重構(gòu)天線陣列的稀疏布陣問題，提出一種基于擴(kuò)展酉矩陣束算法的優(yōu)化設(shè)計算法。首先建立以陣元位置和多組激勵為變量的多方向圖聯(lián)合稀疏優(yōu)化模型，并利用期望方向圖采樣數(shù)據(jù)構(gòu)建Hankel塊矩陣。然后通過centro-Hermitian化處理和酉變換將采樣矩陣從復(fù)數(shù)域轉(zhuǎn)換到實(shí)數(shù)域，舍棄實(shí)矩陣中較小的奇異值對可重構(gòu)線陣進(jìn)行稀疏。最后通過對等價矩陣束的廣義特征值分解估計稀布陣元位置，進(jìn)而得到每個方向圖對應(yīng)的激勵。仿真驗(yàn)證了該方法能夠以陣元非均勻稀疏分布的陣列形式有效實(shí)現(xiàn)多個方向圖的精確重構(gòu)。

陣列信號處理； 稀疏陣列； 方向圖可重構(gòu)天線； 擴(kuò)展酉矩陣束； 特征值分解

伴隨綜合電子戰(zhàn)系統(tǒng)的日益發(fā)展，為滿足通信、導(dǎo)航、電子對抗等功能集成的需求，天線的數(shù)量和復(fù)雜程度大幅增加，利用盡可能少的天線實(shí)現(xiàn)多個不同的功能成為亟待解決的技術(shù)難題[1-2]。作為多功能陣列天線實(shí)現(xiàn)的關(guān)鍵技術(shù)基礎(chǔ)，方向圖可重構(gòu)陣列天線受到廣泛關(guān)注[3-4]，它利用一個天線陣列，根據(jù)實(shí)際的應(yīng)用需求實(shí)時動態(tài)地重構(gòu)天線方向圖，通過方向圖的切換以實(shí)現(xiàn)原先由多個天線陣列完成的多功能、多任務(wù)[5-6]。這樣可以有效節(jié)省平臺空間、降低系統(tǒng)的整體成本，同時與多個任務(wù)需要多個天線實(shí)現(xiàn)，每個天線對應(yīng)單個獨(dú)立任務(wù)的天線系統(tǒng)相比，由于所用天線單元數(shù)量的減少，還可以一定程度地減少雷達(dá)散射截面，以及避免存在于多個天線之間的電磁兼容問題[7]。可重構(gòu)天線作為一種新的天線形式，之所以能夠?qū)崿F(xiàn)天線參數(shù)的重構(gòu)以及不同工作模式的切換，其本質(zhì)是通過改變天線的電流分布實(shí)現(xiàn)的。具體實(shí)現(xiàn)方法大致分為改變天線單元的內(nèi)在結(jié)構(gòu)和改變天線外部的饋電網(wǎng)絡(luò)兩類。第一種方式會增加天線單元的設(shè)計難度，不適合輻射體較小的情況[8]。而改變饋電結(jié)構(gòu)的方式是通過對饋電激勵源本身參數(shù)的改變來實(shí)現(xiàn)方向圖重構(gòu)，不需要對天線單元單獨(dú)設(shè)計，成本較低、更易實(shí)現(xiàn)，近些年國內(nèi)外學(xué)者對此進(jìn)行了相關(guān)研究[5-10]。

文獻(xiàn)[5-6]僅通過改變均勻陣列天線的饋電相位實(shí)現(xiàn)陣列方向圖的控制，簡化了饋電系統(tǒng)，但其自由度較小。文獻(xiàn)[9-10]利用優(yōu)化算法對陣元等間隔布置的陣列天線饋電激勵進(jìn)行控制以實(shí)現(xiàn)方向圖可重構(gòu)。相比于等間隔均勻布陣的方式，非均勻稀疏陣列天線在減少陣元個數(shù)，提高孔徑利用率、抑制互耦等方面具有明顯優(yōu)勢，它在單個天線陣列設(shè)計中得到了很好的應(yīng)用。文獻(xiàn)[11-14]通過優(yōu)化稀布陣列的位置和激勵，能夠以較少的陣元個數(shù)獲得期望的方向圖性能，然而這些稀疏優(yōu)化布陣方法很難直接應(yīng)用到方向圖可重構(gòu)的陣列天線中，這是因?yàn)橛刹煌较驁D求解得到的最優(yōu)稀疏陣元位置不同，很有可能導(dǎo)致陣元間距過小而無法布陣。劉顏回等在文獻(xiàn)[13-14]的基礎(chǔ)上，將矩陣束方法擴(kuò)展到稀疏可重構(gòu)陣列的設(shè)計中，通過激勵的改變實(shí)現(xiàn)不同的方向圖性能。然而由于該方法涉及的矩陣運(yùn)算均在復(fù)數(shù)域進(jìn)行，求得的陣元位置可能為復(fù)數(shù)，對陣元位置的近似處理不能有效保證方向圖的擬合精度。

因此，如何在同一天線孔徑上，選擇少于均勻布陣所需的陣元個數(shù)，通過改變陣元的饋電激勵以實(shí)現(xiàn)不同方向圖的重構(gòu)，是本文重點(diǎn)研究的內(nèi)容。這需要實(shí)現(xiàn)多個方向圖位置和激勵的聯(lián)合求解，并且使不同方向圖共享相同的稀疏陣元位置，僅通過改變饋電激勵以實(shí)現(xiàn)不同方向圖的切換。本文提出一種有效求解上述問題的擴(kuò)展酉矩陣束(Extended Unitary Matrix Pencil,EUMP)算法，在建立多方向圖聯(lián)合稀疏優(yōu)化模型的基礎(chǔ)上，由方向圖采樣數(shù)據(jù)及其共軛構(gòu)建centro-Hermitian矩陣，并利用酉變換將該復(fù)矩陣轉(zhuǎn)化為實(shí)矩陣，舍棄實(shí)矩陣中較小的奇異值來減少可重構(gòu)線陣的陣元數(shù)目，最后根據(jù)等價矩陣束的廣義特征值分解和總體最小二乘準(zhǔn)則得到稀布陣列的一組陣元位置和多組激勵。由于奇異值分解(Singular Value Decomposition, SVD)和特征值分解(Eigenvalue Decomposition, EVD)的計算均在實(shí)數(shù)域進(jìn)行，并可以直接得到陣元位置的實(shí)數(shù)解，該算法具有計算復(fù)雜度低和方向圖擬合度高的優(yōu)勢，利用少量陣元即可重構(gòu)出不同方向圖。

1 EUMP實(shí)現(xiàn)稀疏可重構(gòu)天線陣

1.1 多方向圖聯(lián)合稀疏優(yōu)化模型

假設(shè)均勻方向圖可重構(gòu)線陣由N個全向陣元組成，通過改變饋電激勵可得陣列天線的M種工作模式，即重構(gòu)出M種不同的期望方向圖。陣因子可表示為

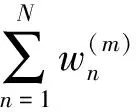
(1)

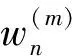
稀疏方向圖可重構(gòu)線陣通過對陣元位置和激勵的聯(lián)合優(yōu)化求解，得到非均勻稀疏分布的單元位置及M組陣元激勵，采用盡可能少的陣元數(shù)Q即可實(shí)現(xiàn)M個期望方向圖的切換，其模型可表示為[15]

(2)

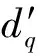
1.2 算法描述

以uk=kΔ=k/K(k=-K,-K+1,…,0,…,K)為采樣點(diǎn)在-1到1間對陣因子進(jìn)行P=2K+1點(diǎn)等間隔均勻采樣，可得

(3)

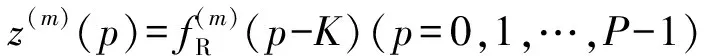
[Ze]D×E=[Z(1)Z(2)…Z(M)]

(4)

(5)

式中：D=L+1，E=M(P-L)，束參數(shù)L滿足N≤L≤P-N。那么，極點(diǎn)rn(n=1,2,…,N)是矩陣束(Z2,Z1)的廣義特征值[16]，即

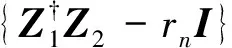
(6)

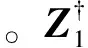
為了降低矩陣運(yùn)算復(fù)雜度，考慮對Hankel塊矩陣Ze實(shí)數(shù)化處理，由于酉變換能夠?qū)entro-Hermitian復(fù)矩陣轉(zhuǎn)變?yōu)閷?shí)矩陣，因其在減少計算量方面的優(yōu)勢而被用于高分辨的子空間類方法中[17-18]。因此，利用酉變換求解包含方向圖采樣信息的實(shí)矩陣，首先需要根據(jù)采樣矩陣Ze構(gòu)造具有centro-Hermitian特性的矩陣Zc，使其滿足[19]：

(7)

式中：上標(biāo)*表示共軛運(yùn)算，ΠD為D階單位反對角置換矩陣，即

(8)

那么，對于復(fù)矩陣Ze，根據(jù)其共軛及單位反對角置換矩陣，相應(yīng)的centro-Hermitian矩陣Zc可表示為

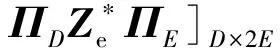
(9)

對Zc進(jìn)行酉變換[20]，可得實(shí)矩陣Zr為

(10)

式中：YD為D階酉矩陣，且有

YD=

(11)

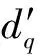
J2Zc=rnJ1Zc

(12)

式中：

(13)

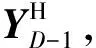
(14)

將式(10)代入，式(14)可簡化為

(15)

根據(jù)酉矩陣和單位反對角置換矩陣的性質(zhì)，式(15)左邊等效為

(16)

結(jié)合式(15)和式(16)，有

(17)

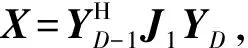
[Re(X)-jIm(X)]Zr=

[Re(rn)+jIm(rn)][Re(X)+jIm(X)]Zr

(18)

由于Re(rn)=cos(k0dnΔ)，Im(rn)=sin(k0dnΔ)，移項(xiàng)可得

-tan(k0dnΔ/2)Re(X)Zr=Im(X)Zr

(19)

因此，-tan(k0dnΔ/2)(n=1,2,…,N)為矩陣束(Im(X)Zr,Re(X)Zr)的廣義特征值。為了減少陣元數(shù)目，對實(shí)矩陣Zr奇異值分解：

(20)

式中：I=min{D,2E}，U=[u1u2…uI]和V=[v1v2…vI]分別為左奇異向量矩陣和右奇異向量矩陣，Σ=diag(σ1,σ2,…,σN,…,σI)為對角矩陣，σ1≥σ2≥…≥σI。N元均勻線陣包含N個非零奇異值，有σi=0(i>N)，但通常只需要更少的非零奇異值就能得到Zr的低階逼近矩陣，該矩陣包含陣元個數(shù)少于N的稀布線陣的方向圖重構(gòu)數(shù)據(jù)，即通過舍棄Σ中較小的奇異值以實(shí)現(xiàn)陣列的稀疏優(yōu)化布陣。因此，-tan(k0dqΔ/2)(q=1,2,…,Q)是矩陣束(Im(X)UL,Re(X)UL)的廣義特征值yq：

{Im(X)UL-yqRe(X)UL}?

{[Re(X)UL]?[Im(X)UL]-yqI}

(21)

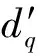
W=(RHR)-1RHF=

(22)

式中：

(23)

1.3 實(shí)現(xiàn)步驟

EUMP利用酉變換將復(fù)數(shù)域的SVD和EVD問題的求解分別等效為實(shí)矩陣的SVD和等價實(shí)矩陣束的EVD，計算量減少約3/4。通過分析EUMP主要步驟的實(shí)數(shù)乘法運(yùn)算次數(shù)可大致估計算法的計算量，該算法共需要(D2E+5D3+1.5Q2D+5Q3+ 1.5Q2P+QPM)次乘法，其計算復(fù)雜度主要由SVD的計算量決定。下面給出該算法實(shí)現(xiàn)方向圖可重構(gòu)稀疏線陣的具體步驟：

步驟1構(gòu)造實(shí)值方向圖采樣矩陣。由M種期望方向圖的采樣數(shù)據(jù)計算擴(kuò)展復(fù)矩陣Ze，并根據(jù)centro-Hermitian處理合成復(fù)矩陣Zc，再通過酉變換求解實(shí)數(shù)據(jù)矩陣Zr。

步驟2奇異值分解。對實(shí)矩陣Zr奇異值分解，保留Q個較大的奇異值以得到相應(yīng)的左奇異向量矩陣UL。

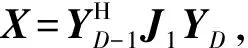
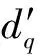
步驟5性能評估。根據(jù)式(26)計算重構(gòu)方向圖與期望方向圖的歸一化匹配誤差：

(24)

2 仿真結(jié)果及分析

基于多方向圖聯(lián)合稀疏優(yōu)化模型，以N=30的均勻可重構(gòu)線陣可實(shí)現(xiàn)的3種典型波束形狀(筆形波束、平頂波束[22]、余割波束[22])為3個期望方向圖進(jìn)行仿真實(shí)驗(yàn)(CPU3.40 GHz，3.46 GB RAM，Matlab2012b)。由于本文算法通過減少實(shí)值方向圖采樣矩陣奇異值的個數(shù)對陣列進(jìn)行稀疏，綜合考慮稀疏率和方向圖擬合程度的要求，奇異值個數(shù)(陣元個數(shù))Q在22～24間取值，可保證可重構(gòu)線陣的稀疏率在73%～80%的條件下，重構(gòu)方向圖與期望方向圖歸一化匹配誤差ξ在1×10-5到1×10-3之間。

2.1 束參數(shù)的選擇

為了研究ξ關(guān)于束參數(shù)L的變化趨勢，進(jìn)行如下仿真。以Q=23為例，對于不同K值，ξ與L的關(guān)系如圖1所示。由于L的取值滿足N≤L≤2K+1-N，在仿真中取K=xN(x=1.5,2.0,2.5,3.0)，則有30≤L≤30 (2x-1)+1。從圖1中可以看出，4條曲線的變化趨勢大致相同，ξ分別在L=61,91,114,137時取得最小值8.537 7×10-5,5.547 8×10-5,5.388 8×10-5,5.315 7×10-5。以K=(2,3)N為例，對于不同Q值，ξ與L的關(guān)系如圖2所示，由圖可知，相同的參數(shù)設(shè)置(同K,L)，陣元個數(shù)越多，方向圖擬合程度越高，圖中標(biāo)出了不同條件下ξ的最小值點(diǎn)。

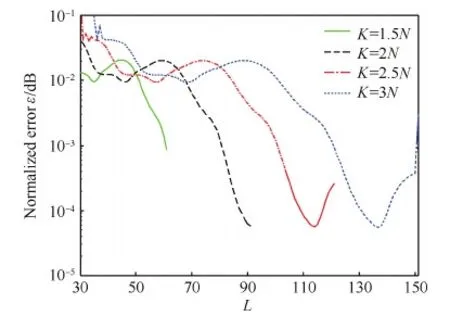
圖1 不同K值下歸一化誤差ξ關(guān)于束參數(shù)L的變化趨勢Fig.1 Behaviors of ξ versus L with different K values

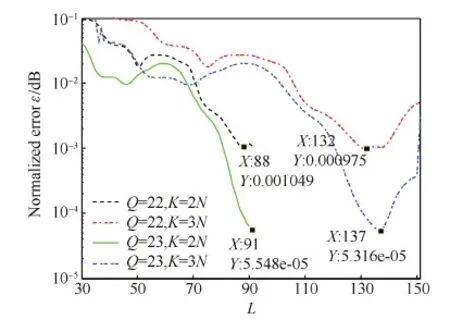
圖2 不同Q值下歸一化誤差ξ關(guān)于束參數(shù)L的變化趨勢Fig.2 Behaviors of ξ versus L with different Q values

2.2 有效性驗(yàn)證

為了驗(yàn)證算法實(shí)現(xiàn)方向圖可重構(gòu)稀疏線陣的有效性，以K=2N為例，分別取Q=23，L=91和Q=22，L=88進(jìn)行仿真。圖3(a)和圖3(b)分別給出了不同陣元個數(shù)u下重構(gòu)方向圖與期望方向圖的比較，從圖中可以看出，相比于均勻可重構(gòu)線陣所需的30個陣元，本文算法節(jié)省約25%的陣元個數(shù)即可有效控制波束形狀，能夠重構(gòu)出與均勻線陣3種期望方向圖性能近似一致的波束方向圖，ξ分別為5.547 8×10-5和1.049 0×10-3。分段截取方向圖曲線的不同區(qū)間進(jìn)行觀察，如圖4(a)和4(b)所示，從圖中可以看出，對于Q=23的情況，本文算法在主瓣賦形區(qū)波束形狀和旁瓣電平均能滿足要求的前提下，通過改變陣元激勵就能夠得到3種與期望方向圖形狀保持一致的波束方向圖，可以實(shí)現(xiàn)與期望波束的高精度擬合。對于Q=22的情況，本文算法在主瓣賦形區(qū)能夠與期望波束匹配，但其旁瓣電平有所升高，對于精確賦形要求較高的應(yīng)用場合，可以通過增加陣元個數(shù)來提高方向圖擬合程度。不同陣元個數(shù)時，可重構(gòu)線陣的陣元位置及相應(yīng)激勵見表1。

為了驗(yàn)證算法在重構(gòu)方向圖擬合精度及計算時間方面的優(yōu)越性，采用文獻(xiàn)[15]算法對上述均勻可重構(gòu)線陣進(jìn)行稀疏，取Q=22，比較兩種算法在相同稀疏率條件下的方向圖性能，具體結(jié)果如表2所示，可以看出，本文提出的EUMP算法具有更小的方向圖匹配誤差，計算時間大約為文獻(xiàn)[15]算法的1/4，這是因?yàn)楸疚乃惴ú捎玫挠献儞Q將主要的矩陣運(yùn)算從復(fù)數(shù)域轉(zhuǎn)換到實(shí)數(shù)域，能夠直接得到陣元位置的實(shí)數(shù)解，提高了方向圖擬合精度，同時復(fù)矩陣運(yùn)算變?yōu)閷?shí)矩陣運(yùn)算也導(dǎo)致了計算量的減少。圖5和圖6給出了文獻(xiàn)[15]算法重構(gòu)方向圖與期望方向圖的比較，由圖可知，該算法可以在保證一定稀疏率的條件下獲得與均勻線陣相一致的主瓣波束，但旁瓣電平明顯增加，旁瓣區(qū)域的方向圖有較大偏差。

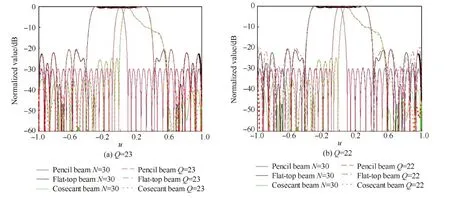
圖3 Q=23 and 22時稀疏可重構(gòu)線陣的方向圖Fig.3 Power patterns radiated by the sparse reconfigurable arrays for Q=23 and 22

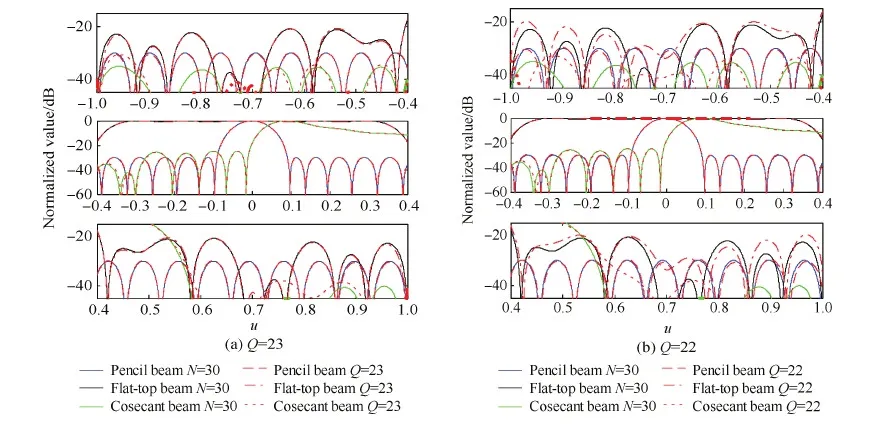
圖4 Q=23 and 22時稀疏可重構(gòu)線陣方向圖的分段截圖Fig.4 Partitioned view of power patterns radiated by the sparse reconfigurable arrays for Q=23 and 22

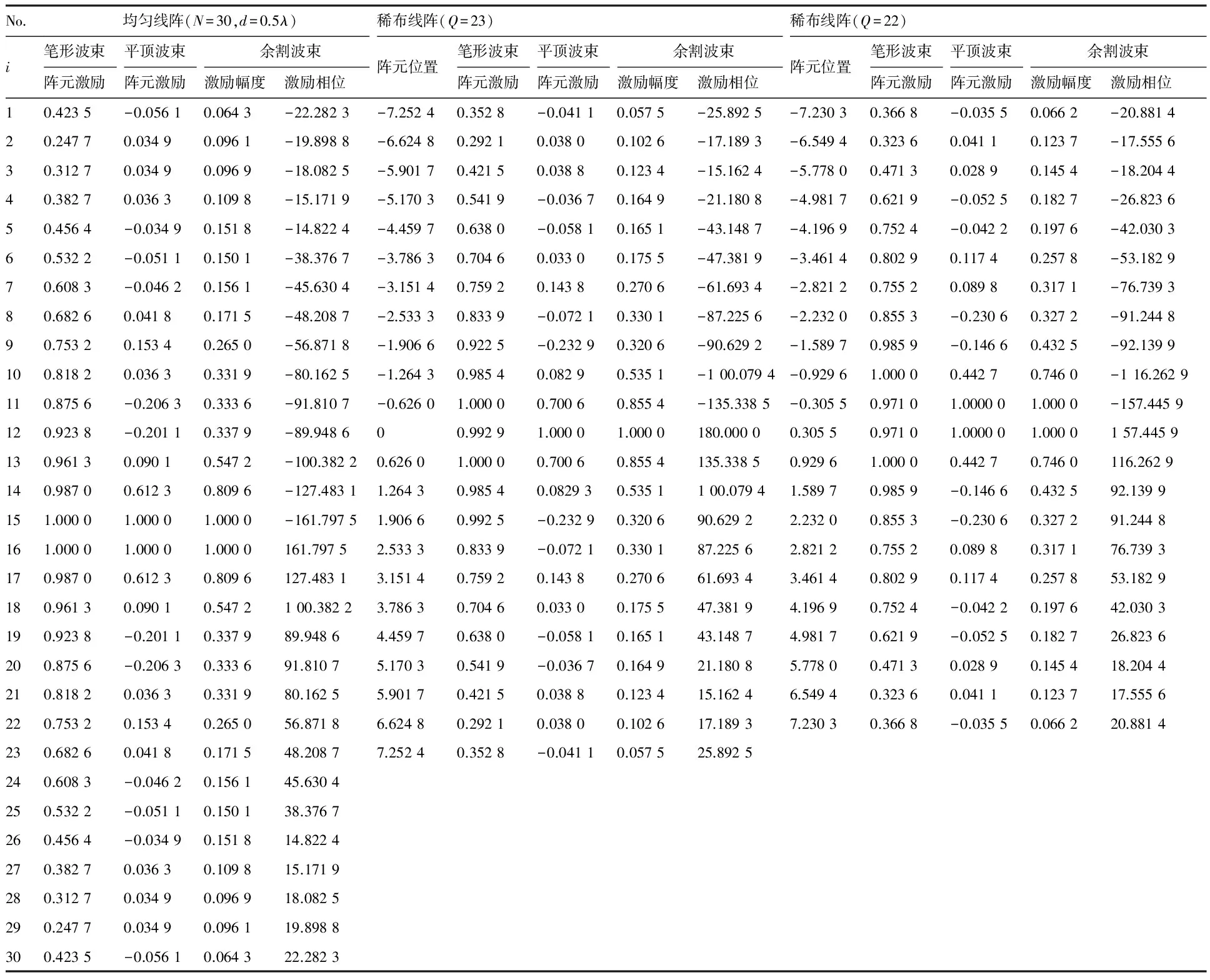
表1 可重構(gòu)線陣的陣元位置和相應(yīng)激勵Table 1 Element positions and excitations radiated by the uniform and the sparse reconfigurable arrays

表2 兩種算法性能的比較Table 2 Performance comparisons of two algorithms

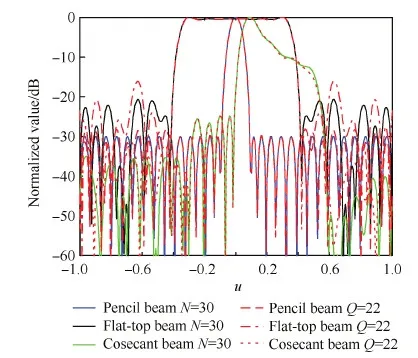
圖5 Q=22時稀疏可重構(gòu)線陣的方向圖[15]Fig.5 Power patterns radiated by the sparse reconfigurable arrays in Ref.[15] for Q=22

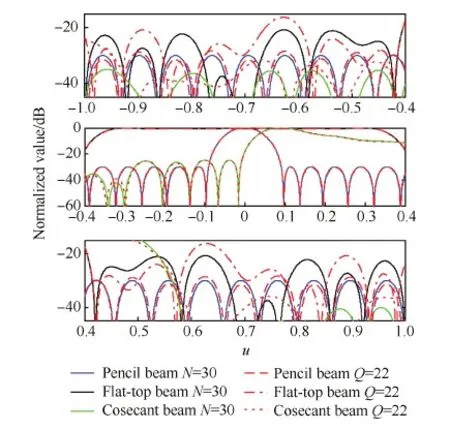
圖6 Q=22時稀疏可重構(gòu)線陣方向圖[15]的分段截圖Fig.6 Partitioned view of power patterns radiated by the sparse reconfigurable arrays in Ref.[15] for Q=22

2.3 敏感性分析

為了分析算法的敏感性，對饋電信號進(jìn)行幅相干擾，研究存在饋電偏差情況下可重構(gòu)陣列的方向圖性能。以本文算法得到的陣元數(shù)為23的稀疏可重構(gòu)線陣為例，對理想陣元激勵的幅度和相位(如表1所示)隨機(jī)擾動，進(jìn)行500次Monte-Carlo仿真。圖7分別給出了方向圖歸一化誤差隨幅相擾動范圍的變化曲線。由圖可知，該算法可以容忍一定程度的饋電幅相誤差，但隨著饋電偏差的增大，算法的性能有所損失。為了保證重構(gòu)方向圖與期望方向圖較高的擬合精度(ξ<2×10-3)，當(dāng)饋電信號的幅度偏差小于理想幅度的±12%，相位偏差小于理想相位的±5%時，該算法可以滿足應(yīng)用要求。圖8給出了饋電幅度偏差為±5%條件下稀疏可重構(gòu)線陣的3種方向圖，從圖中可以看出，筆形方向圖與其期望方向圖最接近，而余割方向圖與期望方向圖的擬合程度較差，也就是說，余割方向圖對于饋電偏差更敏感，該方向圖的精確賦形對饋電激勵的準(zhǔn)確性有更高的要求。

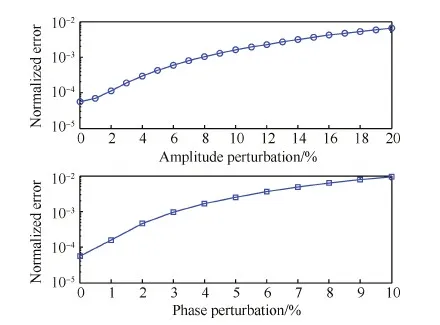
圖7 不同幅相擾動下的方向圖歸一化誤差 Fig.7 Normalized error under different amplitude perturbation and phase perturbation

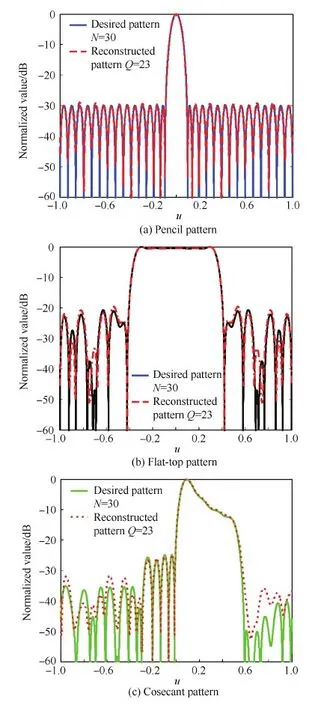
圖8 存在饋電偏差時的筆形方向圖、平頂方向圖以及余割方向圖 Fig.8 Pencil pattern, flat-top pattern and cosecant pattern with feeding perturbation

3 結(jié) 論

1) 建立以陣元位置和多組激勵為變量的多方向圖聯(lián)合稀疏優(yōu)化模型，通過共享相同的稀疏陣元位置，改變每個陣元的饋電激勵以實(shí)現(xiàn)不同方向圖的重構(gòu)。相比于等間距的均勻可重構(gòu)陣列，該稀疏可重構(gòu)陣列模型在減少陣元個數(shù)及抑制互耦等方面具有優(yōu)勢。

2) 提出一種有效求解多方向圖聯(lián)合稀疏優(yōu)化模型的擴(kuò)展酉矩陣束算法。酉變換的引入保證得到的陣元位置為實(shí)數(shù)，有效避免了復(fù)數(shù)解引入的近似處理問題；且奇異值分解和特征值分解均在實(shí)數(shù)域進(jìn)行，計算量較小。因此，該方法具有計算復(fù)雜度低和方向圖擬合度高的特點(diǎn)。

3) 仿真實(shí)驗(yàn)表明該方法能夠以陣元非均勻稀疏分布的陣列形式有效實(shí)現(xiàn)多個方向圖的精確重構(gòu)。

[1] LAGER I E, TRAMPUZ C, SIMEONI M, et al. Application of the shared aperture antenna concept to radar front-ends: advantages and limitations[C]//2010 4th European Conference on Antennas and Propagation (EuCAP), 2010: 1-4.

[2] 趙菲, 齊會穎, 邱磊, 等. 自適應(yīng)動態(tài)Meta粒子群優(yōu)化算法綜合多方向圖共形陣列[J]. 電子與信息學(xué)報, 2012, 34(6): 1476-1482.

ZHAO F, QI H Y, QIU L, et al. Adaptive dynamic meta particle swarm optimization algorithm synthesizing multiple-pattern conformal array[J]. Journal of Electronics & Information Technology, 2012, 34(6):1476-1482 (in Chinese).

[3] HAUPT R L, LANAGAN M. Reconfigurable antennas[J]. IEEE Antennas and Propagation Magazine, 2013, 55(1): 49-61.

[4] KANG W, KIM K. A radiation pattern-reconfigurable antenna for wireless communications[C]//2011 IEEE International Symposium on Antennas and Propagation. Piscataway, NJ: IEEE Press, 2011: 1545-1548.

[5] MORABITO A F, MASSA A, ROCCA P, et al. An effective approach to the synthesis of phase-only reconfigurable linear arrays[J]. IEEE Transactions on Antenna and Propagation, 2012, 60(8): 3622-3631.

[6] VESCOVO R. Reconfigurability and beam scanning with phase-only control for antenna arrays[J]. IEEE Transactions on Antenna and Propagation, 2008, 56(6): 1555-1565.

[7] MAHANTI G K, CHAKRABORY A, DAS S. Design of fully digital controlled reconfigurable array antennas with fixed dynamic range ratio[J]. Journal of Electromagnetic Waves and Applications, 2007, 21(1): 97-106.

[8] DING X, WANG B Z. A millimeter-wave pattern-reconfigurable antenna with a reconfigurable feeding network[J]. Journal of Electromagnetic Waves and Applications, 2013, 27(5): 649-658.

[9] SUBHASHINI K R, KUMAR K P, LALITHA G, et al. Reconfigurable array antennas with side lobe level control by genetic modulation[C]//2011 IEEE Students’ Technology Symposium (TechSym). Piscataway, NJ: IEEE Press, 2011: 123-127.

[10] MANICA L, ROCCA P, MARTINI A, et al. An innovative approach based on a tree-searching algorithm for the optimal matching of independently optimum sum and difference excitations[J]. IEEE Transactions on Antenna and Propagation, 2008, 56(1): 58-66.

[11] ZHAO X W, YANG Q S, ZHANG Y H. Compressed sensing approach for pattern synthesis of maximally sparse non-uniform linear array[J]. IET Microwaves, Antennas & Propagation, 2014, 8(5): 301-307.

[12] OLIVERI G, MASSA A. Bayesian compressive sampling for pattern synthesis with maximally sparse non-uniform linear arrays[J]. IEEE Transactions on Antenna and Propagation, 2011, 59(2): 467-481.

[13] LIU Y H, NIE Z P, LIU Q H. Reducing the number of elements in a linear antenna array by the matrix pencil method[J]. IEEE Transactions on Antenna and Propagation, 2008, 56(9): 2955-2962.

[14] LIU Y, LIU Q H, NIE Z P. Reducing the number of elements in the synthesis of shaped-beam patterns by the forward-backward matrix pencil method[J]. IEEE Transactions on Antenna and Propagation, 2010, 58(2): 604-608.

[15] LIU Y H, LIU Q H, NIE Z P. Reducing the number of elements in multiple-pattern linear arrays by the extended matrix pencil methods[J]. IEEE Transactions on Antenna and Propagation, 2014, 62(2): 652-660.

[16] SARKAR T K, PARK S, KOH J, et al. Application of the matrix pencil method to estimating the SEM (singularity expansion method) poles of source-free transient responses from multiple look directions[J]. IEEE Transactions on Antenna and Propagation, 2000, 48(4): 48-55.

[17] LI J F, ZHANG X F. Unitary subspace-based method for angle estimation in bistatic MIMO radar[J]. Circuits, Systems, and Signal Processing, 2014, 33(2): 501-513.

[18] QIAN C, HUANG L. Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling[J]. IEEE Signal Processing Letters, 2014, 21(2): 140-144.

[19] LEE A. Centrohermitian and skew-centrohermitian matrices[J]. Linear Algebra and Its Application, 1980, 29: 205-210.

[20] HUANG K C, YEH C C. Unitary transformation method for angle of arrival estimation[J]. IEEE Transactions on Signal Processing, 1991, 39(4): 975-977.

[21] 張賢達(dá). 矩陣分析與應(yīng)用[M]. 2版. 北京: 清華大學(xué)出版社, 2013： 11.

ZHANG X D. Matrix analysis and applications[M]. 2nd ed. Beijing: Tsinghua University Press, 2013： 11 (in Chinese).

[22] AKDAGLI A, GUNEY K. Shaped-beam pattern synthesis of equally and unequally spaced linear antenna arrays using a modified tabu search algorithm[J]. Microwave and Optical Technology Letters, 2003, 36(1): 16-20.

Extendedunitarymatrixpencilalgorithmforoptimaldesignofsparsereconfigurableantennaarrays

SHENHaiou,WANGBuhong*

InformationandNavigationCollege,AirForceEngineeringUniversity,Xian710077,China

Aninnovativemethod,extendedunitarymatrixpencil(EUMP)algorithm,isproposedfortheoptimaldesignofsparsereconfigurableantennaarrays.Thejointsparseoptimizationmodelisestablishedwithelementpositionsandexcitationsasthedesignvariables,andanextendedblock-Hankelmatrixcanbeconstructedaccordingtosampledataofthedesiredpattern.Thenthroughcentro-Hermitianmatrixandunitarytransformation,thiscomplex-valuedsamplematrixcanbetransformedintoreal-valuedone,ofwhichsmallersingularvaluesarediscardedtoreducethenumberofantennaelements.Thegeneralizedeigenvaluesofequivalentmatrixpencilareexploitedtoestimatethesparsearrayelementpositionsandtheircorrespondingexcitationsaccurately.Simulationresultsvalidatethatmultiple-patternscanbereconfiguredwithnon-uniformarrangementsbythisalgorithmefficiently.

arraysignalprocessing;sparsearray;patternreconfigurableantenna;extendedunitarymatrixpencil(EUMP)method;eigenvaluedecomposition

2015-12-21；Revised2016-03-29；Accepted2016-06-14；Publishedonline2016-06-201341

2015-12-21；退修日期2016-03-29；錄用日期2016-06-14； < class="emphasis_bold">網(wǎng)絡(luò)出版時間

時間：2016-06-201341

www.cnki.net/kcms/detail/11.1929.V.20160620.1341.002.html

*

.Tel.：029-84791762E-mailwbhyl@aliyun.com

沈海鷗， 王布宏. 擴(kuò)展酉矩陣束算法實(shí)現(xiàn)稀疏可重構(gòu)天線陣的優(yōu)化設(shè)計J． 航空學(xué)報,2016,37(12):3811-3820.SHENHO，WANGBH.ExtendedunitarymatrixpencilalgorithmforoptimaldesignofsparsereconfigurableantennaarraysJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3811-3820.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0191

V219； TN820

A

1000-6893(2016)12-3811-10

沈海鷗女， 博士研究生。主要研究方向： 陣列信號處理、 雷達(dá)信號處理。Tel.: 029-84791772E-mail: haioushen1990@sina.com

王布宏男， 博士， 教授， 博士生導(dǎo)師。主要研究方向： 陣列信號處理、 陣列誤差校正。Tel.: 029-84791762E-mail: wbhyl@aliyun.com

URL：www.cnki.net/kcms/detail/11.1929.V.20160620.1341.002.html

*Correspondingauthor.Tel.：029-84791762E-mailwbhyl@aliyun.com