對(duì)流層延遲模型映射函數(shù)研究

謝劭峰 張朋飛 王新橋 劉立龍

1 桂林理工大學(xué)測(cè)繪地理信息學(xué)院，桂林市雁山街319號(hào)，5410062 廣西空間信息與測(cè)繪重點(diǎn)實(shí)驗(yàn)室，桂林市雁山街319號(hào)，541006 3 東海航海保障中心上海海事測(cè)繪中心，上海市共青路82弄7號(hào)，200086

?

對(duì)流層延遲模型映射函數(shù)研究

謝劭峰1,2張朋飛3王新橋1,2劉立龍1,2

1 桂林理工大學(xué)測(cè)繪地理信息學(xué)院，桂林市雁山街319號(hào)，5410062 廣西空間信息與測(cè)繪重點(diǎn)實(shí)驗(yàn)室，桂林市雁山街319號(hào)，541006 3 東海航海保障中心上海海事測(cè)繪中心，上海市共青路82弄7號(hào)，200086

在介紹經(jīng)驗(yàn)映射函數(shù)NMF和動(dòng)態(tài)映射函數(shù)VMF1、GMF模型的基礎(chǔ)上，利用ECMWF提供的格網(wǎng)數(shù)據(jù)，具體研究和分析了這3種映射函數(shù)1 a中的時(shí)間變化特征及其隨高程、緯度、高度角變化的特點(diǎn)，并比較了3種映射函數(shù)隨高度角的變化對(duì)斜路徑延遲估計(jì)的影響。

GPS數(shù)據(jù)處理；對(duì)流層延遲；斜路徑延遲；映射函數(shù)；時(shí)空變化

在高精度GPS數(shù)據(jù)處理中，對(duì)流層延遲是一個(gè)重要的影響因素。但是，直接求解電波經(jīng)過(guò)對(duì)流層時(shí)各個(gè)方向的對(duì)流層延遲是比較困難的。基于球?qū)ΨQ的假設(shè)，可以用天頂對(duì)流層延遲(ZTD)和映射函數(shù)(MF)的乘積來(lái)表示任意方向上的斜路徑延遲。利用高精度的映射函數(shù)可以更準(zhǔn)確地求出斜路徑延遲，進(jìn)而估算出大氣中不同方向的水汽含量。因此，高精度映射函數(shù)的構(gòu)建成為空間定位數(shù)據(jù)處理與GNSS實(shí)時(shí)遙感空間大氣分布等領(lǐng)域的研究熱點(diǎn)[1]。

1 常用的映射函數(shù)

根據(jù)不同的構(gòu)造方式，映射函數(shù)可以分為3 大類：第一類是把大氣折射積分中的被積函數(shù)按照高度角三角函數(shù)進(jìn)行級(jí)數(shù)展開，然后對(duì)展開項(xiàng)進(jìn)行逐項(xiàng)積分，最后求出大氣折射的延遲，這種方法求得的映射函數(shù)稱為經(jīng)典映射函數(shù)，主要有Saastamoinen模型和Hopfield模型；第二類是上世紀(jì)70年代初期由Marini提出的連分式形式的映射函數(shù)，如Ifadis模型、MTT模型、NMF模型等，這類函數(shù)中的參數(shù)是通過(guò)對(duì)大量的經(jīng)驗(yàn)資料擬合后獲得；第三類是近年發(fā)展起來(lái)的動(dòng)態(tài)映射函數(shù)，這種模型利用數(shù)值天氣模型(numerical weather models, NWM)提供的高時(shí)空分辨率的對(duì)流層折射率數(shù)據(jù)，構(gòu)建高精度的動(dòng)態(tài)映射函數(shù)，如VMF、GMF。本文主要研究NMF、VMF1、GMF 3種映射函數(shù)的時(shí)空變化特征及其對(duì)斜路徑延遲估計(jì)的影響。

1.1 尼爾映射函數(shù)(Niell mapping function,NMF)

Niell利用全球26個(gè)探空氣球站資料，采用美國(guó)標(biāo)準(zhǔn)大氣模式中北緯15°、30°、45°、60°、75°的一月份和七月份的濕度和溫度廓線得出了NMF模型[2]。該模型考慮了南、北半球季節(jié)性的非對(duì)稱性；映射函數(shù)包括干分量md和濕分量mw兩部分，其中干分量中加入了與測(cè)站高程有關(guān)的改正項(xiàng)，能反映大氣隨高度角ε變化的規(guī)律。NMF模型的干分量md可表示為：

(1)

式中，H(ε)為與測(cè)站高程有關(guān)的改正項(xiàng)：

(2)

式中，aht=2.53×10-5,bht=5.49×10-3,cht=1.14×10-3,H為正高。

當(dāng)測(cè)站緯度在15°～75°時(shí)，系數(shù)ad、bd、cd可以通過(guò)下式內(nèi)插得到：

(3)

式中，p表示要內(nèi)插的系數(shù)ad、bd、cd；t為年積日；t0=28為參考時(shí)刻的年積日；不同緯度的系數(shù)對(duì)應(yīng)的平均值pavg和波動(dòng)的幅度值pamp見表1。

測(cè)站緯度小于15°時(shí)，系數(shù)ad、bd、cd的計(jì)算公式為：

(4)

當(dāng)測(cè)站緯度大于75°時(shí)，系數(shù)ad、bd、cd的計(jì)算公式為：

(5)

NMF模型的濕分量mw可表示為：

(6)

當(dāng)測(cè)站緯度在15°～75°時(shí)，濕分量系數(shù)aw、bw、cw的求解和干分量系數(shù)相同。但是由于濕分量占整個(gè)對(duì)流層延遲的10%左右，比例較小，因此只考慮系數(shù)的平均值而不考慮波動(dòng)項(xiàng)，插值公式可簡(jiǎn)化為：

(7)

式中，各個(gè)緯度系數(shù)的平均值見表2。

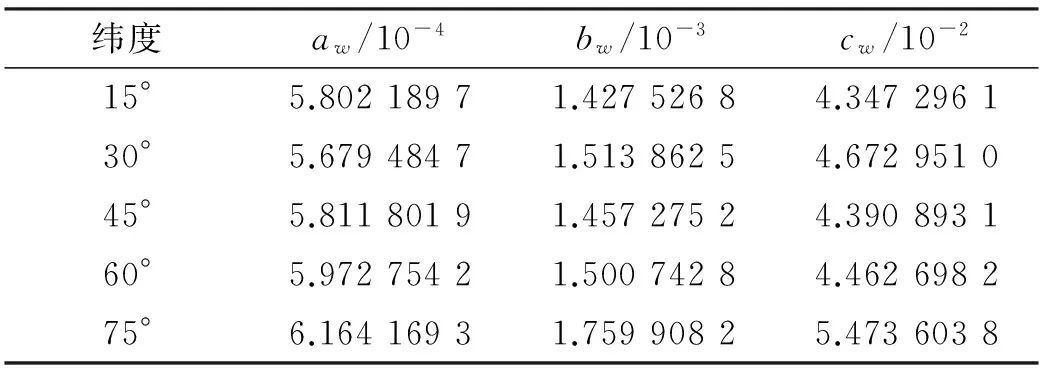
表2 NMF的濕分量?jī)?nèi)插系數(shù)

當(dāng)測(cè)站的緯度小于15°或大于75°時(shí)，分別取15°和75°時(shí)的映射函數(shù)系數(shù)平均值pavg。

1.2 動(dòng)態(tài)映射函數(shù)

1.2.1 維也納映射函數(shù)(Vienna mapping function 1,VMF1)

維也納理工大學(xué)的Boehm和Schuh采用NWM計(jì)算映射函數(shù)的方法得到了VMF模型[3]。VMF和NMF模型具有相同的數(shù)學(xué)表達(dá)式。為使ad和aw更好地符合歐洲中期天氣預(yù)報(bào)中心(ECMWF)的NWM值，對(duì)VMF函數(shù)中系數(shù)b、c的數(shù)學(xué)表達(dá)式進(jìn)行改進(jìn)，得到的模型稱為VMF1模型。它采用ECMWF 40 a的觀測(cè)數(shù)據(jù)資料，重新估計(jì)對(duì)流層映射函數(shù)中系數(shù)b、c的值，而系數(shù)a的值則是利用實(shí)測(cè)數(shù)據(jù)事后時(shí)延34 h生成的2.5°×2°格網(wǎng)列表文件進(jìn)行內(nèi)插獲得。VMF1模型的干分量系數(shù)ad和濕分量系數(shù)aw可以近實(shí)時(shí)地從網(wǎng)站下載(http://mars.hg.tuwien.ac.at/～ecmwf1/)，bd=0.002 9,bw=0.001 46,cw=0.043 91,cd通過(guò)下式擬合得到：

cd=c0+

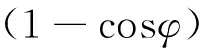
(8)

式中參數(shù)c0、c10、c11和ψ可由索引表查取[3-4]。

1.2.2 全球映射函數(shù)(global mapping function,GMF)

為解決VMF1函數(shù)中系數(shù)ad和aw求解過(guò)程中的時(shí)間延遲問(wèn)題，Boehm等提出了全球映射函數(shù)(GMF)模型[5]，其形式與NMF函數(shù)相似。GMF模型是在VMF1模型基礎(chǔ)上，借鑒NMF建模思想，將年積日、經(jīng)度、緯度、高程作為輸入?yún)?shù)，將模型各個(gè)系數(shù)建立經(jīng)驗(yàn)格網(wǎng)列表文件，按照與年積日有關(guān)的內(nèi)插函數(shù)進(jìn)行內(nèi)插獲得相應(yīng)的模型系數(shù)值。GMF的系數(shù)通過(guò)將VMF1的參數(shù)擴(kuò)展為一個(gè)全球的球諧面格網(wǎng)數(shù)據(jù)，其系數(shù)的確定只需要測(cè)站的位置和年積日。

利用ECMWF提供的40 a全球15°×15°分辨率的溫度、壓強(qiáng)和相對(duì)濕度的月平均廓線，采用高度角為3.3°的射線追蹤法[5-7]，分析1999-09～2002-08的數(shù)據(jù)資料來(lái)確定系數(shù)ad和aw，而b、c仍采用VMF1 模型計(jì)算值。求解GMF模型系數(shù)ad和aw的表達(dá)式為：

(9)

平均值a0、振幅A的算法相同，都是通過(guò)將下面的球諧函數(shù)展開到9階表達(dá)式計(jì)算得到：

(10)

2 NMF、VMF1、GMF模型的時(shí)空變化特征

2.1 3種映射函數(shù)的時(shí)間變化

為了分析這3種映射函數(shù)的時(shí)間變化，選擇武漢站2012年全年的溫度、壓強(qiáng)、相對(duì)濕度等數(shù)據(jù)，分別采用NMF、VMF1和GMF進(jìn)行處理。由于地理位置相同，除了選用的函數(shù)不同外，其他各項(xiàng)參數(shù)都相同，其中高度角設(shè)置為3°，得到的映射函數(shù)的周年分布見圖1。

從圖1可見，與NMF模型相比，GMF、VMF1模型的精度較高、符合較好，但VMF1模型的時(shí)間分辨率比GMF更高；濕映射函數(shù)較干映射函數(shù)離散，函數(shù)值波動(dòng)較大，反映了對(duì)流層中水汽變化的不規(guī)律性；在夏秋季節(jié)映射函數(shù)值比冬春季節(jié)的明顯要小。從圖1還可以看出，NMF的濕映射函數(shù)的數(shù)值在全年保持為常數(shù)，說(shuō)明該模型不能很好地反映濕延遲的年變化規(guī)律。

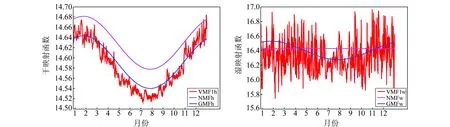
圖1 3種映射函數(shù)的周年分布Fig.1 Annual distribution of three kinds of mapping functions

為研究這3種映射函數(shù)的逐月變化，通過(guò)仰角誤差計(jì)算公式：

(11)

式中，θ0為視在仰角;r0為球心到衛(wèi)星的距離;φ為地心張角;hT為目標(biāo)真實(shí)海拔高度。據(jù)此可求得武漢全年的仰角誤差改正值約為0.251°，取近似值0.25°作為仰角誤差的改正值，從而可得真實(shí)仰角為3.25°。采用射線追蹤法計(jì)算斜路徑延遲和天頂延遲，通過(guò)三角函數(shù)反算計(jì)算映射函數(shù)值。以該值作為真值，與使用3種映射函數(shù)在仰角為3°時(shí)求得的結(jié)果進(jìn)行比較，得到3種映射函數(shù)干分量和濕分量的月平均誤差，見表3。

由表3可知，NMF模型的月平均誤差在冬春季節(jié)較大、夏秋季節(jié)較小，而VMF1、GMF模型的月平均誤差在夏秋季節(jié)較大、冬春季節(jié)較小；在冬春季節(jié)，NMF模型精度比VMF1、GMF模型明顯要差，但在夏秋季節(jié)，NMF模型精度比VMF1、GMF模型要好。VMF1、GMF和NMF的干映射函數(shù)與射線追蹤法取得的真值符合較好，而濕映射函數(shù)符合程度普遍較差，原因可能是因?yàn)楦捎成浜瘮?shù)系數(shù)經(jīng)過(guò)嚴(yán)格推導(dǎo)，而濕映射函數(shù)系數(shù)是忽略了波動(dòng)項(xiàng)影響的近似表達(dá)。

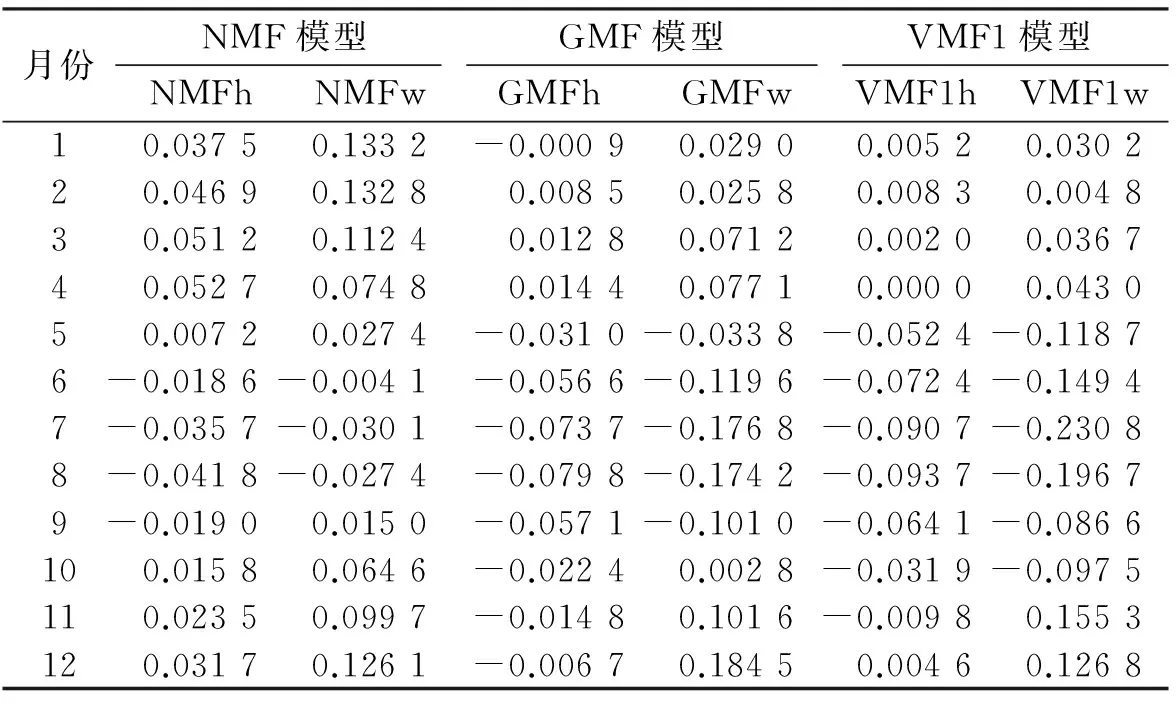
表3 3種映射函數(shù)的月平均誤差

圖2是3種模型獲得的干、濕映射函數(shù)誤差的全年日變化。從圖中可以看出，無(wú)論是干映射函數(shù)還是濕映射函數(shù)，VMF1和GMF都均勻分布于0值附近；夏秋季節(jié)，3種模型干分量多為負(fù)；冬春季節(jié)，GMF模型均為正；GMF、NMF的濕分量冬春季節(jié)均為正，夏秋季節(jié)多為負(fù)，VMF1模型濕分量冬春季節(jié)多為正，夏秋季節(jié)亦多為負(fù)，呈現(xiàn)比較明顯的季節(jié)性特點(diǎn)；在120～270 doy時(shí)，NMF模型干濕分量全部為負(fù)值，說(shuō)明NMF函數(shù)的日變化隨機(jī)性較差，也就是說(shuō)NMF模型比VMF1、GMF這2種模型的穩(wěn)定性要差。

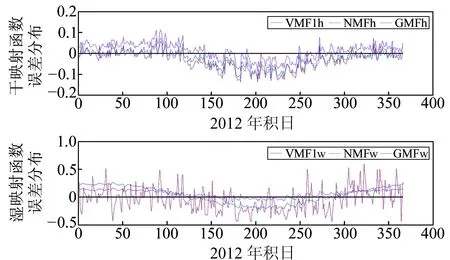
圖2 3種映射函數(shù)誤差的全年日變化Fig.2 Daily variation of three kinds of mapping functions in a year

2.2 3種映射函數(shù)的空間變化

這3種函數(shù)都有相同的輸入?yún)?shù)：高程H、緯度lat和高度角ε。為確定這3種模型的空間變化特性，通過(guò)固定2個(gè)參數(shù)、改變第3個(gè)參數(shù)的方法進(jìn)行數(shù)據(jù)處理。由于我國(guó)大部分地區(qū)處于中緯度，實(shí)驗(yàn)中選取緯度的變化起始點(diǎn)為北緯20°～50°。實(shí)驗(yàn)步驟如下：

1)固定高度角ε=3°和緯度lat=30.61°，使高程H從0 增高到10 km，變化步長(zhǎng)為500 m；

2)固定高程H=23 m和緯度lat=30.61°，高度角ε分別取3°、4°、5°、6°、7°、8°、9°、10°、12°、15°、20°、30°；

3)固定高程H=23 m和高度角ε=3°，緯度變化步長(zhǎng)為2°。

映射函數(shù)值隨高程的變化見圖3。從圖3可以看出，3種函數(shù)的干映射函數(shù)值與高程呈線性關(guān)系，并隨高程的增加而增大；而濕映射函數(shù)值與高程無(wú)關(guān)，為常數(shù)。GMF、VMF1兩種模型的干映射函數(shù)值吻合得較好；VMF1、NMF兩種模型的濕映射函數(shù)值相差較小。

由表4可知，映射函數(shù)的誤差隨高度角的降低而增大；當(dāng)高度角大于7°時(shí)，3種函數(shù)的精度相當(dāng)；在高度角較小時(shí)，濕映射函數(shù)的誤差較干映射函數(shù)大，動(dòng)態(tài)映射函數(shù)GMF、VMF1模型較NMF模型精度高，其中GMF的精度更高、穩(wěn)定性更好，因此在處理低高度角數(shù)據(jù)時(shí)，宜選用動(dòng)態(tài)映射函數(shù)。

從圖4可以看出，隨著緯度的變化，GMF和NMF的干、濕映射函數(shù)值大體呈線性變化，而VMF1的干、濕映射函數(shù)值分布的隨機(jī)性比較大；3種模型的干映射函數(shù)值都隨緯度的增加而增大；GMF和VMF1模型的濕映射函數(shù)值亦隨緯度的增加而增大，但NMF的濕映射函數(shù)值隨緯度增加而有所減小。

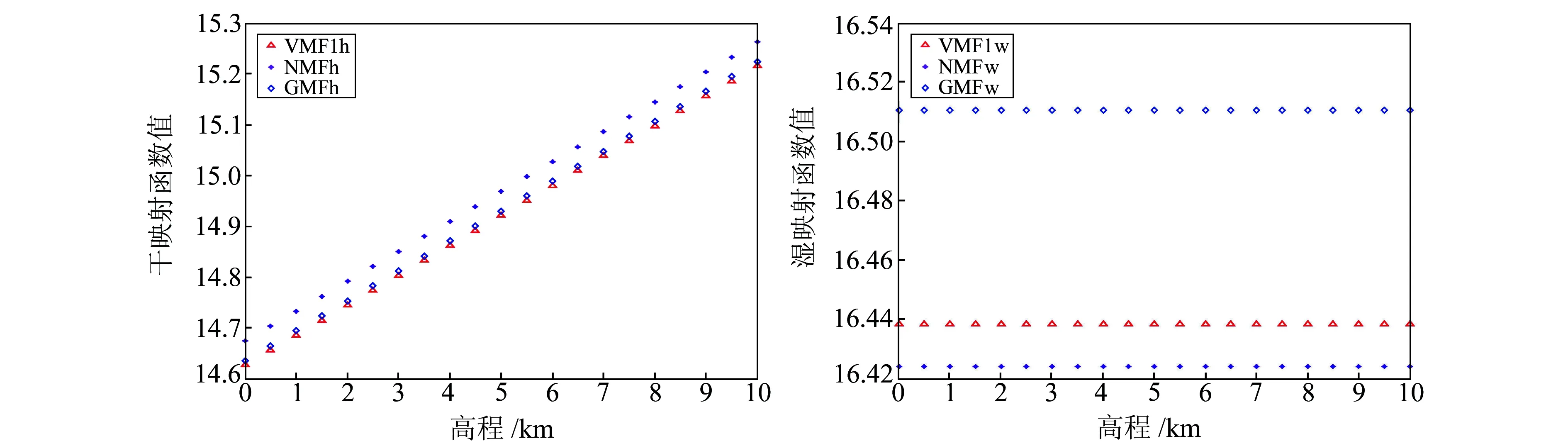
圖3 3種映射函數(shù)值隨高程的變化Fig.3 Variation with height of three kinds of mapping functions’ value

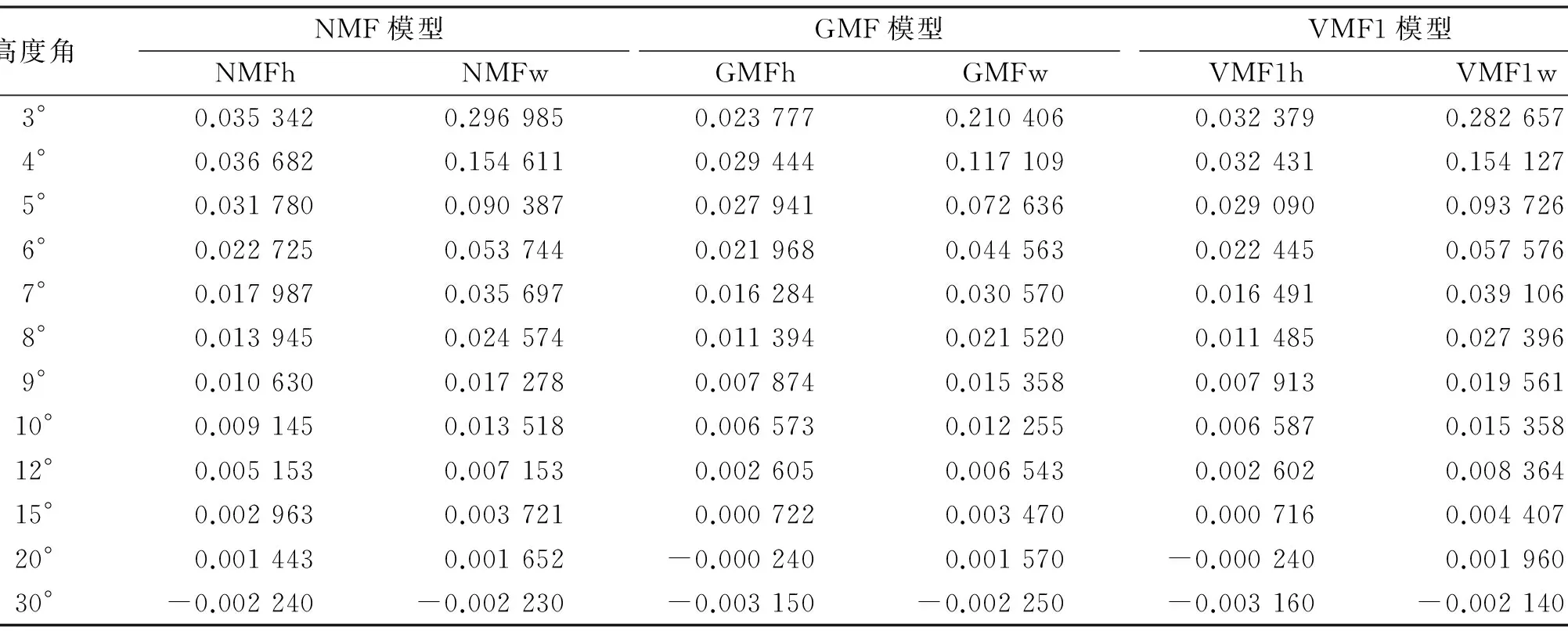
高度角NMF模型GMF模型VMF1模型NMFhNMFwGMFhGMFwVMF1hVMF1w3°0.0353420.2969850.0237770.2104060.0323790.2826574°0.0366820.1546110.0294440.1171090.0324310.1541275°0.0317800.0903870.0279410.0726360.0290900.0937266°0.0227250.0537440.0219680.0445630.0224450.0575767°0.0179870.0356970.0162840.0305700.0164910.0391068°0.0139450.0245740.0113940.0215200.0114850.0273969°0.0106300.0172780.0078740.0153580.0079130.01956110°0.0091450.0135180.0065730.0122550.0065870.01535812°0.0051530.0071530.0026050.0065430.0026020.00836415°0.0029630.0037210.0007220.0034700.0007160.00440720°0.0014430.001652-0.0002400.001570-0.0002400.00196030°-0.002240-0.002230-0.003150-0.002250-0.003160-0.002140

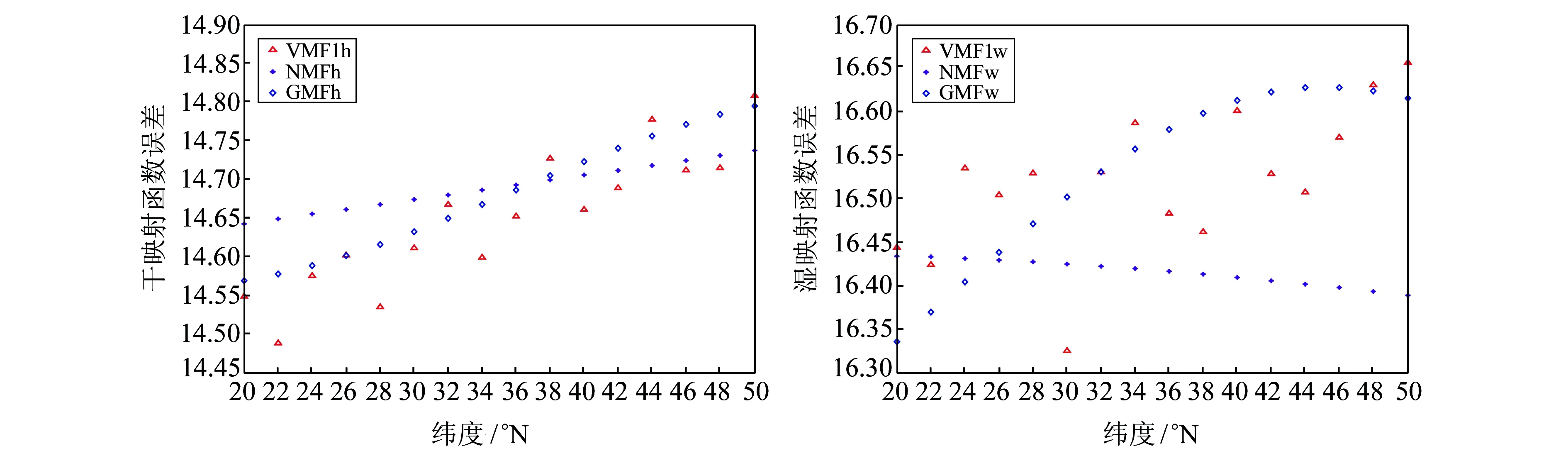
圖4 3種映射函數(shù)誤差隨緯度的變化Fig.4 Variation with latitude of three kinds of mapping functions’ error

3 3種映射函數(shù)對(duì)斜路徑延遲估計(jì)的影響

選用2012年積日150 d的URUM站數(shù)據(jù)，不考慮電波的方位角，僅僅設(shè)置高度角為變量，分別計(jì)算3種映射函數(shù)的斜路徑延遲，結(jié)果見表5。由表5可知，在高度角為1.87°時(shí)，3種模型計(jì)算的斜路徑延遲差別明顯，其中GMF與VMF1相差95.4 mm，GMF與NMF相差80.2 mm，NMF與VMF1相差15.2 mm；當(dāng)高度角為7.07°時(shí)，GMF與VMF1相差5.6 mm，GMF和NMF相差4.3 mm，VMF1和NMF相差1.3 mm；當(dāng)高度角大于等于15°時(shí)，3種映射函數(shù)求得的斜路徑延遲之差均小于1 mm。可見，當(dāng)高度角較大時(shí)，3種映射函數(shù)計(jì)算的斜路徑延遲相當(dāng)，無(wú)明顯差別；但是隨著高度角的降低，求得的斜路徑延遲的差值逐漸增大。因此在計(jì)算低高度角數(shù)據(jù)的斜路徑延遲時(shí)，應(yīng)注意選擇合適的映射函數(shù)。

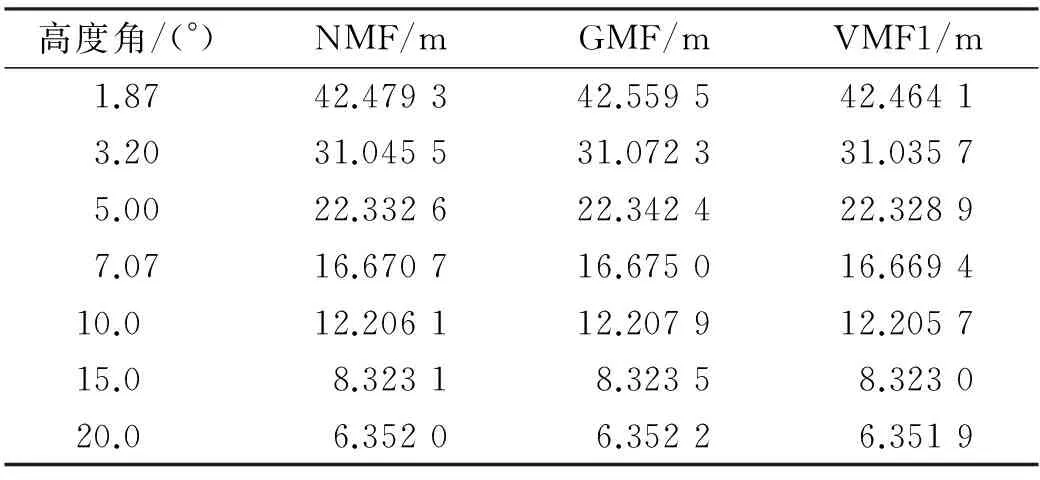
表5 URUM站3種映射函數(shù)解算的斜路徑延遲

4 結(jié) 語(yǔ)

映射函數(shù)誤差在時(shí)間變化方面，3種函數(shù)均呈現(xiàn)比較明顯的季節(jié)變化，冬春季節(jié)與夏秋季節(jié)差異比較明顯。在空間變化方面，隨著緯度和高程的增加，映射函數(shù)誤差相應(yīng)增大；映射函數(shù)誤差隨高度角的降低而增大；高度角較大時(shí)，3種函數(shù)的精度相當(dāng)，但在低高度角時(shí)，GMF、VMF1模型均較NMF模型精度高。3種模型計(jì)算低高度角數(shù)據(jù)的斜路徑延遲時(shí)差別明顯，此時(shí)應(yīng)注意映射函數(shù)的選擇。

[1] 張雙成，葉世榕，劉經(jīng)南 等.動(dòng)態(tài)映射函數(shù)最新進(jìn)展及其在GNSS遙感水汽中的應(yīng)用研究[J].武漢大學(xué)學(xué)報(bào)：信息科學(xué)版，2009,34(3):280-283(Zhang Shuangcheng, Ye Shirong, Liu Jingnan, et al. Latest Progress of Dynamic Mapping Functions and Its Application to GNSS Retrieved Water-Vapor[J].Geomatics and Information Science of Wuhan University, 2009,34(3):280-283)

[2] Niell A. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths[J]. Journal of Geophysical Research: Solid Earth, 1996,101(B2):3 227-3 246

[3] Boehm J, Schuh H. Vienna Mapping Functions in VLBI Analysis[J].Geophysical Research Letters, 2004, 31(1)

[4] Boehm J, Cerveira P, Schuh H, et al. The Impact of Tropospheric Mapping Functions Based on Numerical Weather Models on the Determination of Geodetic Parameters[C]. IAG Proceedings, Cairns, 2005

[5] Boehm J, Niell A, Tregoning P, et al. Global Mapping Function(GMF):A New Empirical Mapping Function Based on Numerical Weather Model Data[J].Geophysical Research Letters, 2006,33(7):199-208

[6] 張瑜，袁秋林. 雷達(dá)至目標(biāo)的電波射線描跡方法研究[J]. 河南師范大學(xué)學(xué)報(bào):自然科學(xué)版, 2006,34(2): 50-53(Zhang Yu, Yuan Qiulin. The Method Research of Radiowave Radial Track Description from Radar to Objective[J].Journal of Henan Normal University: Natural Science, 2006,34(2): 50-53)

[7] 郭際明，章迪，史俊波，等.利用射線追蹤法分析三種典型對(duì)流層映射函數(shù)在中國(guó)區(qū)域的精度[J].武漢大學(xué)學(xué)報(bào):信息科學(xué)版，2015,40(2): 182-187(Guo Jiming, Zhang Di, Shi Junbo,et al. Using Ray-Tracing to Analyse the Precision of Three Classical Tropospheric Mapping Functions in China[J].Geomatics and Information Science of Wuhan University, 2015,40(2): 182-187)Research on the Mapping Functions for Tropospheric Delay Model

XIEShaofeng1,2ZHANGPengfei3WANGXinqiao1,2LIULilong1,2

1 College of Geomatics and Geoinformation, Guilin University of Technology, 319 Yanshan Street, Guilin 541006, China 2 Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China 3 Hydrography Department Shanghai Maritime Safety Administration, Donghai Navigation Safety Administration,7 Lane 82, Gongqing Road,Shanghai 200086, China

On the basis of introducing the empirical mapping function NMF and the dynamic mapping functions VMF1 and GMF, using one year’s grid data provided by ECMWF, the time varying characteristics of these three mapping functions and their variations with height, latitude and elevation angle are concretely researched and analyzed are compared. Finally,we compare the influence on slant path delay with the variations of elevation angle in the three kinds of mapping functions are compared.

GPS data processing; tropospheric delay; slant path delay; mapping function; temporal and spatial variation

National Natural Science Foundation of China, No.41064001, 41541032; Guangxi Key Laboratory of Spatial Information and Geomatics Foundation, No.15-140-07-11, 14-045-24-10.

ZHANG Pengfei,assistant engineer, majors in GPS data processing and application, E-mail: 879333424@qq.com.

2015-12-13

項(xiàng)目來(lái)源：國(guó)家自然科學(xué)基金(41064001, 41541032)；廣西空間信息與測(cè)繪重點(diǎn)實(shí)驗(yàn)室基金(15-140-07-11, 14-045-24-10)。

謝劭峰，副教授，主要研究方向?yàn)镚PS數(shù)據(jù)處理與應(yīng)用，E-mail: xieshaofeng111@126.com。

張朋飛，助理工程師，主要研究方向?yàn)镚PS數(shù)據(jù)處理與應(yīng)用，E-mail: 879333424@qq.com。

10.14075/j.jgg.2016.11.001

1671-5942(2016)011-0941-05

P228

A

About the first author:XIE Shaofeng, associate professor, majors in GPS data processing and application,E-mail: xieshaofeng111@126.com.