基于二階錐規(guī)劃的相干信號(hào)寬零陷自適應(yīng)波束形成

黃 超，張劍云，朱家兵，王 瑜

(1.解放軍電子工程學(xué)院，安徽 合肥 230037；2.中國電子科技集團(tuán)公司第三十八研究所，安徽 合肥 230088)

?

基于二階錐規(guī)劃的相干信號(hào)寬零陷自適應(yīng)波束形成

黃 超1，張劍云1，朱家兵2，王 瑜1

(1.解放軍電子工程學(xué)院，安徽 合肥 230037；2.中國電子科技集團(tuán)公司第三十八研究所，安徽 合肥 230088)

針對(duì)傳統(tǒng)自適應(yīng)波束形成器在相干干擾位置出現(xiàn)快速變化時(shí)，輸出性能下降，甚至干擾抑制失效的問題，提出了一種基于二階錐規(guī)劃(SOCP)的相干信號(hào)寬零陷自適應(yīng)波束形成算法。該算法首先對(duì)接收數(shù)據(jù)協(xié)方差矩陣進(jìn)行Toeplitz重構(gòu)，然后重構(gòu)了干擾加噪聲協(xié)方差矩陣并對(duì)其進(jìn)行零陷展寬處理；接著在保證期望方向波束無失真前提下，約束主瓣寬度和旁瓣電平，使得波束形成器干擾和噪聲的輸出功率最小；最后將該問題轉(zhuǎn)化為凸優(yōu)化中的二階錐規(guī)劃問題，并使用凸優(yōu)化工具箱進(jìn)行快速求解。仿真實(shí)驗(yàn)表明，該算法可以在兼顧全部陣列性能指標(biāo)的前提下，在相干干擾區(qū)域形成寬零陷。

二階錐規(guī)劃；相干干擾；協(xié)方差矩陣重構(gòu)；零陷展寬；凸優(yōu)化

0 引言

自適應(yīng)波束形成技術(shù)被廣泛應(yīng)用于雷達(dá)、聲吶和無線電通訊等領(lǐng)域[1-3]，它可以根據(jù)環(huán)境的變化自適應(yīng)地調(diào)整權(quán)值在干擾方向上形成零陷，能夠有效地抑制空間干擾，提高系統(tǒng)的輸出信干噪比。然而在工程實(shí)際中，干擾源和信號(hào)接收陣列都有可能是快速移動(dòng)的。在這種情況下，當(dāng)自適應(yīng)權(quán)值的收斂速度達(dá)不到干擾源相對(duì)于天線接收陣列的相對(duì)移動(dòng)速度，就會(huì)出現(xiàn)加權(quán)訓(xùn)練數(shù)據(jù)與應(yīng)用數(shù)據(jù)失配，使得干擾源方向從天線方向圖的零陷位置移出，從而使得干擾抑制失敗。

零陷展寬算法可以有效地抑制快速運(yùn)動(dòng)的干擾信號(hào)。Mailloux算法[4]是最傳統(tǒng)的零陷展寬算法，該算法通過構(gòu)造錐化矩陣對(duì)接收數(shù)據(jù)協(xié)方差矩陣進(jìn)行加權(quán)來展寬干擾方向的零陷。文獻(xiàn)[5—6]在Mailloux算法的基礎(chǔ)上，從統(tǒng)計(jì)模型和旋轉(zhuǎn)導(dǎo)向矢量方面對(duì)原算法進(jìn)行了改進(jìn)。這類算法在展寬零陷的同時(shí)會(huì)使零陷深度變淺，而且算法魯棒性較差。對(duì)此，文獻(xiàn)[7]結(jié)合投影變換技術(shù)和對(duì)角加載技術(shù)，提出了一種新的零陷展寬算法，該方法能在展寬零陷的同時(shí)加深零陷，對(duì)參數(shù)的選取具有較強(qiáng)的穩(wěn)健性。文獻(xiàn)[8]針對(duì)模型失配的情況，通過重構(gòu)和優(yōu)化干擾加噪聲協(xié)方差矩陣、估計(jì)真實(shí)導(dǎo)向矢量，提出了一種魯棒的自適應(yīng)零陷展寬算法。

上述零陷展寬自適應(yīng)波束形成算法都是采用樣本協(xié)方差矩陣求逆方法(SMI)來形成波束方向圖的。SMI方法簡單穩(wěn)定，但基于該算法的零陷展寬算法不能兼顧自適應(yīng)波束形成的全部性能指標(biāo)，在形成寬零陷的同時(shí)會(huì)抬高旁瓣電平并展寬主瓣波束。同時(shí)，上述零陷展寬算法只適用于期望信號(hào)和干擾相互獨(dú)立的情況，當(dāng)信號(hào)和干擾相干時(shí)，必須先對(duì)其做解相干處理。

本文針對(duì)上述問題，提出了基于二階錐規(guī)劃(SOCP)的相干信號(hào)寬零陷自適應(yīng)波束形成算法。

1 基本理論

1.1 SOCP的基本概念

SOCP理論是凸優(yōu)化理論的最新分支。SOCP方法在二階錐空間內(nèi)尋找最優(yōu)解，由于其尋優(yōu)速度較快，被廣泛地應(yīng)用到工程實(shí)際中。

所謂SOCP，就是在有限個(gè)二階錐的笛卡爾乘積的仿射子空間的交集上極小化一個(gè)線性函數(shù)。其數(shù)學(xué)表述一般為：

minqTx

subject to:

‖Ai+bi‖2≤ciTx+di,i=1,2,…,m

(1)

式(1)中，x∈Rn為優(yōu)化變量，q∈Rn, Ai∈R(ni-1)×n,bi∈R(ni-1)，ci∈Rn,di∈R，約束條件中的范數(shù)為標(biāo)準(zhǔn)的L2范數(shù)或歐幾里得范數(shù)，即‖u‖2=(uTu)1/2。則標(biāo)準(zhǔn)的k維二階錐記為：

(2)

1.2 自適應(yīng)波束形成模型

圖1所示為M元均勻直線陣。

圖1 M元均勻直線陣Fig.1 M-elements uniform linear array

圖1中，設(shè)定有一個(gè)窄帶遠(yuǎn)場(chǎng)期望信號(hào)從θ0方向入射到該陣列，P個(gè)干擾信號(hào)從θi(i=1,2，…,P)方向入射到該陣列。信號(hào)波長為λ，陣元間距d=λ/2，則第n個(gè)陣元接收到的數(shù)據(jù)為：

n=1,2，…，M

(3)

式(3)中，s0(t)為期望信號(hào)，sk(t),k=1,2，…,P為干擾信號(hào)。τn(θi),i=0,1，…,P是期望信號(hào)和干擾信號(hào)傳播到第n個(gè)陣元的時(shí)延，vn(t)是第n個(gè)陣元接收到的噪聲。可將陣列接收信號(hào)矢量表示為：

X(t)=As(t)+v(t)

(4)

其中，X(t)=[x1(t),x2(t),…,xM(t)]T是陣列輸出矢量，A是信號(hào)和干擾的陣列導(dǎo)向矢量，s(t)是入射信號(hào)矢量，v(t)是陣列噪聲矢量，假設(shè)v(t)是均值為0、方差為σ2的高斯白噪聲。

s(t)=[s1(t),s2(t),…,sP(t)]T

(5)

v(t)=[v1(t),v2(t),…,vM(t)]T

(6)

A=[a(θ0),a(θ1),…，a(θP)]

(7)

a(θi)=[1,exp(φ),…，exp((M-1)φ)]T

(8)

陣列接收信號(hào)的協(xié)方差矩陣為：

R=E[X(t)XH(t)]

(9)

在實(shí)際情況中，陣列接收信號(hào)的協(xié)方差矩陣是通過有限次的快拍估計(jì)出來的，假設(shè)快拍數(shù)為L，則陣列接收信號(hào)的協(xié)方差矩陣估計(jì)值為：

(10)

則基于最小方差無失真響應(yīng)(MVDR)準(zhǔn)則進(jìn)行自適應(yīng)波束形成，其代價(jià)函數(shù)為

(11)

2 基于SOCP的相干信號(hào)寬零陷自適應(yīng)波束形成算法

2.1 算法原理

針對(duì)傳統(tǒng)自適應(yīng)波束形成算法對(duì)快速移動(dòng)的相干干擾抑制失效的問題，本文提出了一種基于SOCP的相干信號(hào)寬零陷自適應(yīng)波束形成算法。該算法首先進(jìn)行解相干處理，對(duì)接收數(shù)據(jù)協(xié)方差矩陣進(jìn)行Toeplitz重構(gòu)，使其包含信號(hào)和干擾的所有方位信息，然后重構(gòu)了干擾加噪聲協(xié)方差矩陣并對(duì)其進(jìn)行零陷展寬處理，接著在保證期望方向波束無失真前提下，約束主瓣寬度和旁瓣電平，使得波束形成器的輸出功率最小，最后將該問題轉(zhuǎn)化為凸優(yōu)化中的二階錐規(guī)劃問題，并使用凸優(yōu)化工具箱進(jìn)行快速求解。

1)Toeplitz矩陣重構(gòu)

(12)

2)干擾加噪聲協(xié)方差矩陣重構(gòu)

(13)

(14)

3)零陷展寬處理

(15)

則經(jīng)過零陷展寬處理后的相干干擾和噪聲的自相關(guān)矩陣為：

(16)

在式(16)中， “°”表示Hadamard乘運(yùn)算。則對(duì)于快速移動(dòng)的相干干擾，基于MVDR準(zhǔn)則進(jìn)行自適應(yīng)波束形成的代價(jià)函數(shù)為：

(17)

2.2 相干信號(hào)寬零陷自適應(yīng)波束形成優(yōu)化模型

對(duì)均勻直線陣進(jìn)行加權(quán)處理，令加權(quán)向量為w=[w1,w2,…，wM]，則陣列的方向圖為：

F(θ)=wHa(θ)

(18)

a(θ)是均勻直線陣的陣列導(dǎo)向矢量。現(xiàn)將整個(gè)空域分為主瓣區(qū)ΘML和旁瓣區(qū)ΘSL，并進(jìn)行離散化處理，令φm∈ΘML,(m=1,…,P)，φs∈ΘSL,(s=1,…,S)。為了保證波束中期望方向的響應(yīng)不會(huì)出現(xiàn)失真，則必須約束wHa(θ0)=1；同時(shí)考慮到天線陣列的工作需要和性能要求，自適應(yīng)形成的方向圖的主瓣波束寬度和旁瓣電平水平必須得到約束，約束條件為:

(19)

(20)

式(20)中，對(duì)加權(quán)系數(shù)進(jìn)行范數(shù)約束：‖w‖≤ξ，可以提高自適應(yīng)波束形成對(duì)隨機(jī)噪聲誤差的穩(wěn)定性。

2.3 優(yōu)化模型的SOCP形式

(21)

由式(21)可知，原優(yōu)化問題已轉(zhuǎn)化為范數(shù)優(yōu)化問題，顯然，優(yōu)化模型是一個(gè)典型的凸優(yōu)化問題，可轉(zhuǎn)化為SOCP形式進(jìn)行快速求解。

則可將模型(21)描述問題的SOCP表示為：

(22)

3 仿真分析

實(shí)驗(yàn)1 算法的有效性驗(yàn)證

假設(shè)數(shù)據(jù)接收陣列為均勻直線陣，陣元數(shù)目為M=16。窄帶遠(yuǎn)場(chǎng)期望信號(hào)的入射角度為0°，信噪比SNR=0 dB。干擾1信號(hào)和干擾2信號(hào)分別從-30°和40°方向入射到接收陣列，干噪比均為INR=30 dB。期望信號(hào)與干擾1和干擾2均相干。信號(hào)波長為λ，陣元間距d=λ/2。約束期望信號(hào)的入射角度范圍為φ=[-5°,5°]，零陷展寬的寬度為10°，約束波束主瓣寬度為20°，設(shè)置零陷深度控制參數(shù)b=2，快拍數(shù)設(shè)為200，則在不同的旁瓣電平約束條件下，本文算法自適應(yīng)形成波束如圖2、圖3。

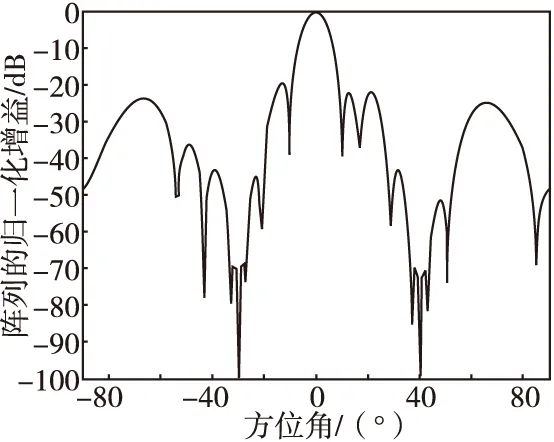
圖2 約束PSLL≤-20 dBFig.2 Constraint of PSLL≤-20 dB

圖3 約束PSLL≤-26 dBFig.3 Constraint of PSLL≤-26 dB

如圖2、圖3所示，本文算法能夠在在保證期望方向波束無失真前提下，嚴(yán)格約束主瓣寬度和旁瓣電平高度，并在快速移動(dòng)的相干干擾方位附近形成寬零陷。同時(shí)也可看出，旁瓣電平的高低會(huì)影響到自適應(yīng)波束形成時(shí)干擾零陷的深度；當(dāng)約束的旁瓣電平較低時(shí)，干擾零陷的深度也會(huì)隨之變淺。

實(shí)驗(yàn)2 零陷深度控制參數(shù)b的選擇分析

實(shí)驗(yàn)參數(shù)選取同實(shí)驗(yàn)1，期望信號(hào)、干擾1和干擾2完全相干，約束旁瓣電平PSLL≤-20 dB，分別取b的值為1、2和3，自適應(yīng)形成波束如圖4所示。其余參數(shù)不變，b的值從1到3逐漸變化，每隔0.2取值一次，并做100次Monte Carlo實(shí)驗(yàn)，自適應(yīng)波束形成后的輸出信干噪比如圖5所示。

圖4 b取不同值時(shí)的波束圖Fig.4 Beamforming with different values of b

圖5 輸出SINR隨著b取值的變化Fig.5 The relationship between output SINR with b

由圖4可知，當(dāng)b取不同值時(shí)，本文算法都可以在滿足主波束寬度和旁瓣電平的約束條件下在相干干擾周圍形成寬零陷。而且隨著b取值的增大，零陷深度也會(huì)加深，對(duì)相干干擾的抑制能力增強(qiáng)。由圖5可知，在其他約束條件不變的前提下，自適應(yīng)波束形成器的輸出信干噪比先隨著b的增大而增大，但當(dāng)b>1.4后，輸出信干噪比隨著b的增大開始逐漸降低。這是因?yàn)殡S著b的增大，空間譜密度函數(shù)P(θ)中的干擾分量逐漸增大，干擾零陷的深度也隨之加深，強(qiáng)相干干擾得到了抑制，陣列輸出的SINR逐漸增大；但當(dāng)干擾零陷的深度足以完全抑制強(qiáng)相干干擾后，b的增大不再影響輸出信號(hào)中的干擾分量，而噪聲分量得到增強(qiáng)的幅度又遠(yuǎn)大于期望信號(hào)的增強(qiáng)幅度，此時(shí)隨著b的增大，陣列輸出的SINR逐漸降低。因此，對(duì)于零陷深度控制參數(shù)b的選取，必須綜合考慮實(shí)際情況對(duì)干擾零陷深度和輸出信干噪比的要求。

實(shí)驗(yàn)3 本文算法性能隨信噪比和快拍數(shù)的變化情況

假設(shè)期望信號(hào)、干擾1和干擾2完全相干，約束旁瓣電平PSLL≤-20 dB，調(diào)整快拍數(shù)從50均勻變化至500，每次取值做100次Monte Carlo實(shí)驗(yàn)，其余參數(shù)選取同實(shí)驗(yàn)1，得到本文算法的輸出信干噪比同快拍數(shù)的關(guān)系如圖6所示。接著再確定快拍數(shù)為200，令輸入信噪比從-30 dB均勻變化到30 dB，每間隔10 dB做100次Monte Carlo實(shí)驗(yàn)，得到本文算法的輸出信干噪比同輸入信噪比的關(guān)系如圖7所示。

圖6 輸出SINR隨快拍數(shù)的變化Fig.6 The relationship between output SINR with snapshots

圖7 輸出SINR隨輸入SNR的變化Fig.7 The relationship between output SINR with input SNR

由圖6可知，輸出SINR對(duì)快拍數(shù)的變化不敏感，當(dāng)快拍數(shù)較小時(shí)(50)，本文算法就可以穩(wěn)定的達(dá)到想要的輸出SINR，因此本文算法可用于對(duì)信號(hào)進(jìn)行實(shí)時(shí)處理。由圖7可看出，本文算法得到的輸出SINR隨輸入SNR的增大而線性增大，這是因?yàn)楸疚乃惴s束了期望信號(hào)方向無失真，輸入SNR的增大會(huì)提高輸出中的信號(hào)分量，這將改善信號(hào)的檢測(cè)效果。

4 結(jié)論

本文提出了一種基于SOCP的相干信號(hào)寬零陷自適應(yīng)波束形成算法。該算法首先進(jìn)行了解相干處理，然后重構(gòu)了干擾加噪聲協(xié)方差矩陣并對(duì)其進(jìn)行零陷展寬處理；接著在保證期望方向波束無失真前提下，約束主瓣寬度和旁瓣電平，使得波束形成器的輸出功率最小；最后將該問題轉(zhuǎn)化為凸優(yōu)化中的二階錐規(guī)劃問題，并使用凸優(yōu)化工具箱進(jìn)行快速求解。仿真驗(yàn)證表明，基于SOCP的相干信號(hào)寬零陷自適應(yīng)波束形成算法可以在兼顧全部陣列性能指標(biāo)的前提下，在相干干擾方位形成寬零陷。

[1]LO K W. Adaptive array processing for wide-band active sonars[J]. IEEE Oceanic Enginerring, 2004, 29(7):837-846.

[2]楊志偉, 賀順, 廖桂生,等. 子空間重構(gòu)的一類自適應(yīng)波束形成算法[J]. 電子與信息學(xué)報(bào), 2012, 34(9):2051-2057.

[3]Thushara K G, Len Bruton, Pan Agathoklis. 7ay (PFA) signals using Real-time spatio-temporal 3D FIR frustum digital filters[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(6):202.

[4]Mailloux R J. Covariance matrix augmentation to produce adaptive array pattern roughs[J]. Electronics Letters, 1995, 31(10):771-772.

[5]李榮峰, 王永良, 萬山虎. 自適應(yīng)方向圖干擾零陷加寬方法研究[J]. 現(xiàn)代雷達(dá), 2003, 25(2):42-45.

[6]武思軍, 張錦中, 張署. 陣列波束的零陷加寬算法研究[J]. 哈爾濱工程大學(xué)學(xué)報(bào)，2004, 10(5):658-661.

[7]李文興, 毛曉軍, 孫亞秀. 一種新的波束形成零陷展寬算法[J]. 電子與信息學(xué)報(bào), 2014, 36(12):2882-2888.

[8]范展, 梁國龍, 王逸林. 一種零陷展寬魯棒自適應(yīng)波束形成算法[J]. 電子與信息學(xué)報(bào), 2013, 35(11):2764-2770.

[9]唐玲, 宋宏, 陳明舉,等. 基于Toeplitz矩陣重構(gòu)的相干信源DOA估計(jì)算法[J]. 航天電子對(duì)抗, 2010, 26(4):15-17.

[10]Yujie G, Leshem A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering Vector estimation[J]. IEEE Transactions on Signal Processing, 2012, 60(7):3881-3885.

Adaptive Beamforming of Coherent Signals with Null Widening Based on SOCP

HUANG Chao1, ZHANG Jianyun1, ZHU Jiabing2,WANG Yu1

(1. Electronic Engineering Institute of PLA, Hefei 230037, China；2. No.38 Research Institute of CETC, Hefei 230088, China)

Because the traditional adaptive beamformer suffers from the output performance degradation and even interference suppression failure when the position of the coherent interference moves, a adaptive beam-forming of coherent signals with null widening based on second order cone programming(SOCP) was proposed. Firstly, the algorithm formed a Toeplitz matrix based on covariance matrix of received data. Secondly, the interference-plus-noise covariance matrix was reconstructed and optimized, and null widening technique was used in the covariance matrix. Thirdly, the optimum beamforming was designed with this method according to the rule of minimizing the beamformer’s output power of interferences and noise while keeping the distortionless response in the direction of desired signal and keeping constant side-lobe level and beamwidth. At last, the original problem was translated into SOCP problem, which could be solved effectively via convex optimization toolbox. Simulation results showed that the proposed algorithm could form a wide null in the strong coherent interference position under the premise of taking all the performance of array into account .

second order cone programming(SOCP); coherent interference; covariance matrix reconstruction; null widening; convex optimization

2016-04-05

中國博士后科學(xué)基金項(xiàng)目資助(2014M552606)；安徽省自然科學(xué)基金項(xiàng)目資助(1408085MF111);中國博士后科學(xué)基金特別資助項(xiàng)目(2015T81083)

黃超(1991—)，男，安徽舒城人，碩士研究生，研究方向：雷達(dá)信號(hào)處理和陣列信號(hào)處理。E-mail：18226658179@163.com。

TN911.7

A

1008-1194(2016)05-0117-06