引信后坐保險機構斜置設計方案
劉 宣,聞 泉,王雨時,張志彪
(南京理工大學機械工程學院,江蘇 南京 210094)
?
引信后坐保險機構斜置設計方案
劉 宣,聞 泉,王雨時,張志彪
(南京理工大學機械工程學院,江蘇 南京 210094)
針對引信后坐保險機構安全和可靠解除保險之間的矛盾,提出了引信后坐保險機構斜置設計方案。該方案是將傳統的軸線與引信軸線平行或重合的后坐保險機構相對于引信軸線斜置一定角度設置。應用剛體動力學理論分析了引信后坐保險機構斜置設計動態特性,并給出了算例。仿真驗證結果表明:后坐保險機構斜置設計有助于提高勤務處理彈丸和引信意外跌落時引信安全性,即有助于提高引信防止意外解除保險的性能,而正常解除保險性能不會受到影響。
引信;后坐保險機構;安全性
0 引言
保險機構是引信的重要組成部分,用來保證發火機構、隔爆機構及其他機構在勤務處理過程中處于保險狀態,而只有在發射或其他預定條件下才能解除保險,使引信處于待發狀態。
引信后坐保險機構作為慣性保險機構的一種,其應用最為普遍。文獻[1]分析了引信后坐機構勤務處理安全性計算公式,介紹了最大響應計算方法,并進一步研究了機構運動特性;文獻[2]介紹了引信單行程保險機構運動特性及保險機構慣性件速度響應計算方法;文獻[3]研究了引信經典后坐保險機構對過載時間的響應特性,得到了不同后坐過載曲線下引信經典彈性后坐保險機構和剛性后坐保險機構解除保險響應特性;文獻[4]介紹了引信后坐保險機構設計的沖擊響應方法,使后坐保險機構的分析與設計更加高效;文獻[5]利用Working Model 3D軟件對引信雙自由度后坐保險機構進行計算機仿真計算,并結合具體實例進行了結構優化設計;文獻[6]研究了引信雙自由度后坐保險機構動態響應特性,運用分段求解耦合微分方程組的方法得出機構位移響應。
以上文獻只是針對引信后坐保險機構運動特性進行了理論分析或仿真研究,并未對低后坐過載條件下引信后坐保險機構安全和可靠解除保險之間的矛盾進行討論。針對此問題,誕生了各種阻尼式后坐保險機構,如曲折槽后坐保險機構、雙自由度后坐保險機構等。本文基于彈丸和引信跌落沖擊的方位特性,即彈丸和引信傾斜跌落時的沖擊遠低于垂直跌落時沖擊的事實,提出引信經典后坐保險機構斜置設計方案。
1 彈丸跌落沖擊響應特性
引信后坐保險機構的安全性設計一直是分析研究的重點與難點,機構的設計必須滿足:在裝卸、運輸、儲存和跌落等勤務處理過程中處于安全狀態;使彈藥在目標或目標區正常引爆時必需能夠可靠解除保險。通常,設計者都是利用彈丸在發射時產生的后坐力作用時間較長,而勤務處理時偶然跌落產生的沖擊力作用時間較短這一特性[7],來解決引信后坐保險機構安全和可靠解除保險之間的矛盾。
彈丸發生意外跌落的姿態是不確定的,且不同的跌落姿態會對彈丸的沖擊特性產生影響。文獻[8]對不同跌落姿態下彈丸沖擊特性進行了研究,結果表明垂直跌落時加速度峰值比傾斜30°(彈丸軸線與豎直線的夾角)跌落時增大45%,比傾斜60°跌落時增大79%;文獻[9]采用數值模擬方法研究子彈藥以不同落角撞擊混凝土介質的沖擊響應,結果表明垂直跌落時加速度峰值比傾斜15°跌落時增大35%,比傾斜30°跌落時增大55%。上述文獻跌落沖擊結果存在差異的主要原因是選取的仿真結構模型和材料模型不同,但都表明垂直跌落對彈丸的沖擊影響最大。
事實上,在垂直跌落時,彈丸或引信底部觸碰跌落目標部分強度和剛度最大,全部動能均由彈丸或引信底部承受,因而形成的沖擊過載最大,對引信后坐保險機構的沖擊影響也最大。而在非垂直跌落時,彈丸或引信底部觸碰跌落目標部分只是局部,強度和剛度較低,形成的沖擊過載較小。
2 引信后坐保險機構斜置設計原理
2.1 構建物理模型
引信斜置后坐保險機構是將傳統的軸線與引信軸線平行或重合的后坐保險機構相對于引信軸線斜置一定角度α設置,如圖1所示。該機構由保險件(慣性體1)、被保險件(鋼珠2)、本體3和抗力件(慣性簧4)組成,其中α為斜置角度。發射或跌落時,慣性體受后坐慣性力作用,下沉到一定距離,其中跌落時該距離不足以釋放被保險件(鋼珠2),而發射時該距離要足以釋放被保險件(鋼珠2),從而解除保險。
2.2 構建數學模型
如圖1所示的引信斜置后坐保險機構:在機構處于保險狀態情況下,慣性簧有一定的預壓量,其抗力作用于慣性筒,且慣性筒在引信體的反作用力及摩擦力的作用下,處于平衡狀態;在機構處于發射或跌落狀態下,后坐慣性力開始作用于慣性筒,隨著后坐力的增大,慣性筒開始運動并逐漸解除保險。根據后坐保險機構運動特性,得到質量塊受力特性,如圖2所示,其中F1是引信體對慣性筒的反作用力、F是慣性簧對慣性筒的彈性抗力、FN是慣性筒駐室側壁對慣性筒的擠壓作用力、Ff是慣性筒受到駐室側壁的摩擦力、FS是引信后坐慣性力。
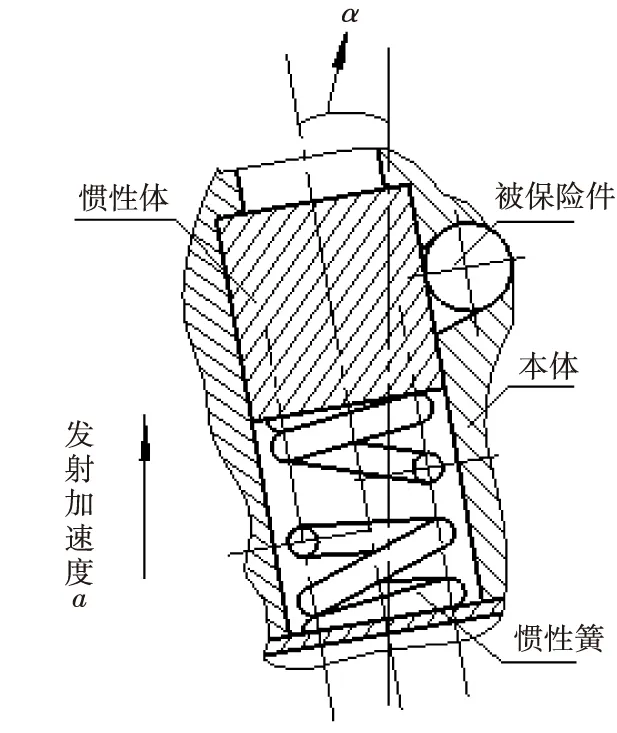
圖1 引信斜置后坐保險機構Fig.1 Inclined design of Fuze Setback Arming Device
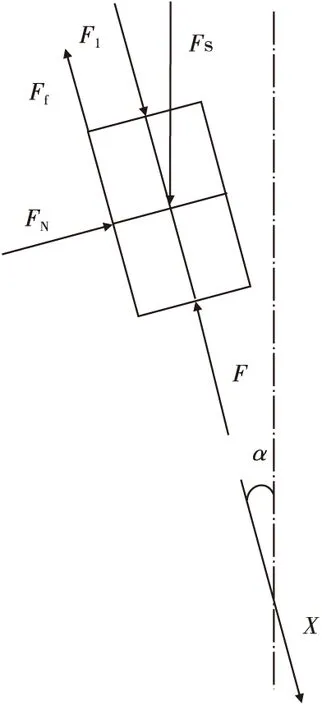
圖2 質量塊受力特性Fig.2 Mass mechanical characteristics
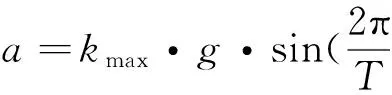
將質量塊的運動過程分為兩個階段:把發射或跌落開始的時間到質量塊開始運動的時間(記為臨界值點t0)作為第一階段;把臨界值點t0到后坐過載(或跌落沖擊過載)作用結束的時間作為第二階段。分析慣性筒運動特性可知:
1)第一階段(0≤t≤t0)
(1)
2)第二階段(t0≤t≤T/2)
(2)
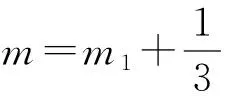
由式(2)可得慣性筒運動微分方程:
(3)
對式(3)求解得到:
(4)
將t=t0時,x=0,x′=0的初始條件代入公式(4)求出C1和C2:

將C1和C2代入式(4)進一步化簡,得
由質量塊受力特性以及式(1)至式(4)可知:
1) 在已知機構設計參數的條件下,kmax、T、α是決定引信后坐保險機構解除保險作用時間的關鍵因素:隨著kmax、T的增大,引信后坐保險機構更易于解除保險;隨著α的增加,引信后坐保險機構更不易于解除保險。
2) 引信后坐保險機構斜置設計質量塊開始運動的必要條件是:
kmaxmg(cosα-μsinα)sin(2πt/T)-k′λ≥0。
3) 由于斜置角度α的引入以及摩擦因素的存在,引信后坐保險機構斜置設計可靠解除保險即質量塊沿著斜面運動而不發生自鎖的必要條件是:
α<90°-arctan u。
2.3 算例分析
選用兩組機構設計參數對引信后坐保險機構斜置設計動態特性進行數值分析和仿真比較研究,兩組機構設計參數分別來源于不同的文獻,如表1所列。摩擦系數μ取為0.15。

表1 機構設計參數
設計初期一般可以估取無包裝的裸露彈藥1.5 m高度垂直跌落到鑄鐵板或鋼板時引信內部零部件所受到的沖擊過載最大量值為7 000~15 000g,作用時間約為150~250 μs。本文取最大沖擊過載系數kmax=10 000,作用時間t=100 μs對后坐保險機構進行跌落計算,得到兩組設計參數在不同斜置角度α下對應的慣性體位移與作用時間關系,如圖3所示。
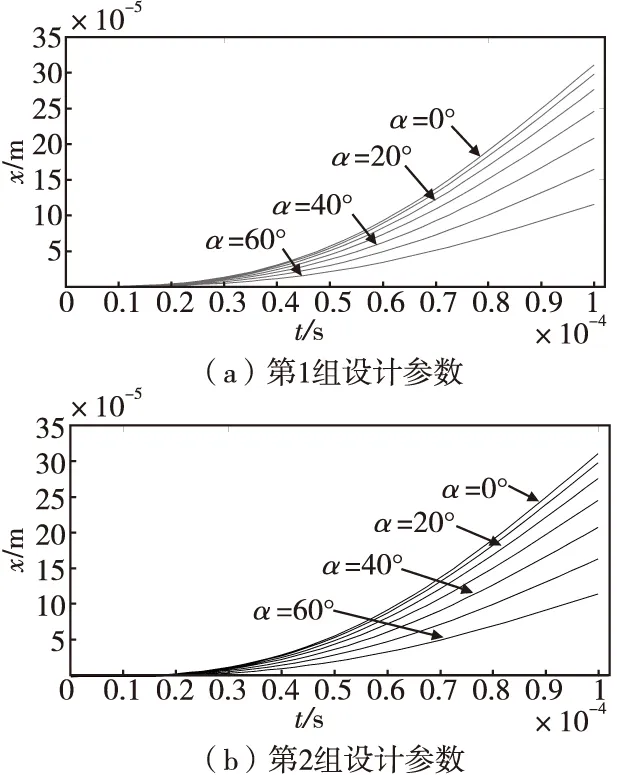
圖3 跌落沖擊作用下不同斜置角度α對應的慣性體位移與作用時間關系Fig.3 Correspondence between displacement and time of inertial body under drop impact
利用表1中的兩組機構設計參數,最大后坐過載kmax=10 000,作用時間t=1.2 ms對后坐保險機構進行發射計算,得到兩組設計參數在不同斜置角度α下對應的慣性體位移與作用時間關系,如圖4所示。
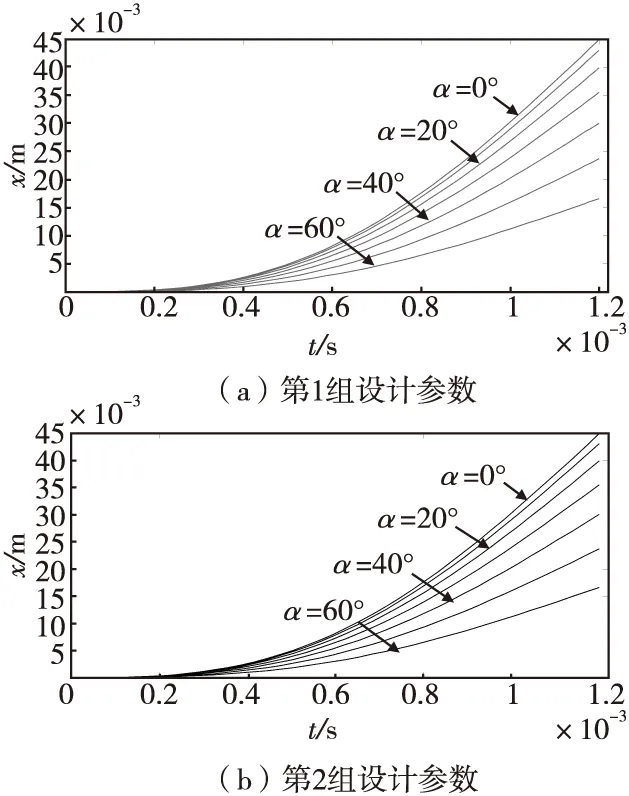
圖4 發射后坐過載作用下不同斜置角度α對應的慣性體位移與作用時間關系Fig.4 Correspondence between displacement and time of inertial body under emission overload effect
由圖3和圖4可看出,斜置角度α對引信后坐保險機構運動特性有顯著影響:無論是跌落沖擊作用還是發射后坐過載作用,不同斜置角度α對應的x-t曲線數值上都有明顯的差異;隨著α的增加,相同作用時間下慣性體的位移明顯減小。
3 仿真驗證結果分析
為進一步探究斜置角度α對引信后坐保險機構安全和解除保險性能的影響,驗證理論分析的正確性,運用ADAMS軟件對后坐保險機構斜置運動特性進行仿真分析,同樣取表1的機構設計參數作為仿真參數,且過載系數kmax、作用時間t與理論分析時相同。建立仿真簡化模型,該模型由斜置側壁,運動質量塊,柔性體彈簧組成,如圖5所示。設置質量塊、斜置側壁材料屬性,賦予其質量特性;設置彈簧屬性,給k′、λ 賦值;給運動質量塊添加移動副,并在移動副上設置摩擦特性(μ取為0.15);給運動質量塊施加后坐力(或跌落沖擊力)FS;定義運動質量塊與斜置側壁間的接觸。

圖5 仿真模型Fig.5 Simulation model
由于2組機構參數相差較小且從得到的結果來看,無論是仿真值還是理論值兩組設計參數對應的結果數值非常接近,所以在此只對表1中的第1組設計參數得到的數值結果列表分析:得到發射后坐過載作用下不同斜置角度α對應的解除保險作用時間(表2);由于在跌落沖擊作用下本算例中后坐保險機構不足以解除保險,但為了直觀地分析斜置角度α對引信后坐保險機構的影響,表3列出了不同斜置角度α對應的沖擊過載作用時間t=100 μs時慣性筒的位移。
在發射后坐過載或跌落沖擊作用一定的條件下,分析表2和表3數據可得:
1) 理論結果與仿真結果比較接近,證明了理論分析的可信性。ADAMS軟件無法賦予彈簧質量特性,經驗證彈簧質量對結果的影響比較小,誤差在0.5%以內;摩擦系數μ可能是影響誤差的主要因素,驗證表明摩擦系數μ值減小,總體平均誤差值也減小,但幅度并不明顯。
2) 引信后坐保險機構斜置設計有助于提高其安全性,即有助于提高防止意外解除保險的性能,而正常解除保險性能一般不會受到影響。

表2 發射后坐過載作用下不同斜置角度α對應的解除保險作用時間

表3 跌落沖擊作用下不同斜置角度α對應的t=100 μs時慣性筒位移
4 結論
本文提出了引信后坐保險機構斜置設計方案,該方案是將傳統的軸線與引信軸線平行或重合的后坐保險機構相對于引信軸線斜置一定角度α設置,應用剛體動力學理論進行了理論分析并應用ADAMS軟件仿真研究了發射和跌落時引信后坐保險機構斜置設計動態特性。仿真驗證結果表明:引信后坐保險機構斜置設計有助于防止意外解除保險,而正常解除保險則不會受影響;引信后坐保險機構斜置設計提高了勤務處理彈丸和引信意外跌落時的引信安全性,有利于解決引信后坐保險機構安全和可靠解除保險之間的矛盾。
[1]李世義.后坐機構平時安全性研究[J]. 兵工學報,1983(2):50-63.
[2]GJB/Z 135-2002.引信工程設計手冊[S]. 北京:中國人民解放軍總裝備, 2002.
[3]李來福,王雨時,聞泉.引信經典后坐保險機構對過載時間的響應特性[J].四川兵工學報, 2014(7):147-152.
[4]陳慶生. 沖擊振動理論與應用 [M]. 北京:國防工業出版社, 1989.
[5]秦文.雙自由度后坐保險機構的計算機動態仿真[J].探測與控制學報,2003,25(1):57-59.
[6]曹瑩,王雨時. 引信雙自由度后坐保險機構動態響應特性分析 [J]. 探測與控制學報,2008,30(2):47-50.
[7]《引信設計手冊》編寫組.引信設計手冊[S]. 北京:國防工業出版社,1978.
[8]邦志輝. 水聲對抗子母彈結構沖擊響應研究[D]. 南京: 南京理工大學,2014.
[9]南宇翔,蔣建偉,王樹有,等.子彈藥落地沖擊響應數值模擬及實驗驗證[J].振動與沖擊, 2013(3):182-187.
[10]嚴慎武. 新型制導炮彈安全與解除保險裝置設計研究 [D]. 南京: 南京理工大學,2012.
Inclined Design of Fuze Setback Arming Device
LIU Xuan,WEN Quan,WANG Yushi,ZHANG Zhibiao
(Mechanical Engineering school, NUST, Nanjing 210094, China)
For the contradiction between safety and reliability of fuze setback arming device, the inclined design of fuze setback arming device was put forward.The program made the fuze axis inclined some degrees to the fuze axis. Dynamic characteristics of inclined design of fuze setback arming device was analyzed by rigid body dynamics theory.The results showed that the inclined design of fuze setback arming device contributes to improve the fuze safety when the projectile and fuze fall accidentally, and the performance of normal arming was not affected.
fuze;setback arming device;inclined design;safety
2015-12-15
劉宣(1989—),男,山東濟寧人,碩士研究生,研究方向:引信系統分析和機構動力學。E-mail:15564864028@163.com。
TJ43
A
1008-1194(2016)05-0010-05

