多視角中反思，甄別通性通法

◇　山東　閆靈巧　夏佑偉

(作者單位：山東省鄒城市第一中學)

?

多視角中反思，甄別通性通法

◇山東閆靈巧夏佑偉

一題多解是啟發和引導同學們從不同的視角出發,探索不同解題思路的一種解題活動,主要目的是培養和鍛煉同學們的思維,探索適應一般情形的最優化的通性通法.

在本題的分析中部分同學認為數列{an}與{bn}的公共項由an=bn求得,即4n-1=3n+2,只有1項.但通過列舉出2數列的前幾項：

{an}: 3,7,11,15,19,23,27,31,35,39,43,47,51,55,59,….

{bn}: 5,8,11,14,17,20,23,26,29,32,35,38,41,44,47,….

可見,2個數列的公共項是11,23,35,47,…,易發現該數列是首項為11、公差為12的等差數列,則

cn=11+12(n-1)=12n-1.

對于上面的2個數列公共項問題,解題思路雖然自然簡潔,但是作為解答題并不嚴謹,下面從多種視角對此題進行探究,并尋找簡潔的通法.

1　選擇一個數列,從整體上尋找問題突破口

設an=bm=ck,則ck=4n-1=3m+2.所以

an+1=4(n+1)-1=3m+2+4=3(m+2)?{bn},

an+2=4(n+2)-1=3m+2+8=3(m+3)+1?{bn},

an+3=4(n+3)-1=3m+2+12=3(m+4)+2=

bm+4∈{bn},

故ck+1=an+3,ck+1-ck=an+3-an=12,即{cn}構成公差為12的等差數列.又因為c1=a3=11,所以

cn=11+12(n-1)=12n-1.

反思1) 規范了解題步驟,再次鞏固探究成果,還可將上面的解題程序推廣到非等差問題的求解; 2) 本題采用直接將表達式和bn=3n+2相比較,可直接判斷出該項屬于數列{bn}中的某一項.當然也可以利用多元不定方程是否有整數解來判斷是否為公共項; 3) 本題選擇{an}進行討論,只需討論an+1、an+2、an+3這3項,便可找到公共項．若選擇數列{bn},則需討論bm+1、bm+2、bm+3、bm+4這4項.道理一想便知,公差越大,該數列中的公共項離得越近,因此盡量選擇公差較大的數列討論.這一原理不經親身體驗感悟不會深刻.

2　從多元不定方程視角,利用數的整除性求解

抓住數列的公共項等價于方程an=bm有解這一點,自然想到求解這個多元不定方程,這是本題的一個重要思路.

m+1=4k,k∈N*.

①

故m=4k-1,所以bm=b4k-1=3(4k-1)+2=12k-1,即cn=12n-1.

反思1)也可由式①得n=3k,a3k=4(3k)-1=12k-1，即cn=12n-1；2)等式4n-1=3m+2中的常數項恰好能湊成公差3或4,很容易想到提取公因式,如果不是這樣呢?

對于數列{bn}來講,其中b3,b10,b17,…都是{an}、{bn}的公共項,所以ck=b7k-4=2(7k-4)+7=14k-1(或者ck=a2k-1=7(2k-1)+6=14k-1).

可見,“利用多元不定方程有整數解”的方法處理2個等差數列的公共項也是一種通法.

3　從指數方程視角,利用二項式定理解方程

如果數列{an}是等比數列,數列{bn}是等差數列,那么方程an=bm就是一個含有指數的方程,在高中階段和指數有關的整除問題還有二項式定理.顯然利用二項式定理解不定方程也是一個不錯的選擇.

反思1上述問題中,由于等比數列{an}的項變化要比等差數列{bn}的快,數列{an}中的相鄰的公共項之間距離只間隔1項,即ck=am,ck+1=am+2,而等差數列{bn}中的相鄰的公共項之間的距離就相當遠,假如bm=ck是第k個公共項,那么下一個公共項是b4m+2=ck+1,再次驗證了2個等差數列公共項應該盡量在公差較大的數列中找ck與ck+1之間的關系.

此外,對于一個等比數列與一個等差數列的公共項問題,前面案例中所研究的解題方法同樣適用.可以看出,變式訓練不僅是一種鞏固,更多的是讓我們不斷地加深對解題方法本質的認識.

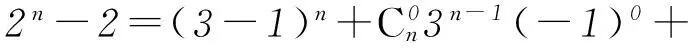
所以當n為奇數時,右式能被3整除.又因為m為正整數, 所以n為大于1的奇數,所以cn=22n+1.

反思2上述問題中,bn=3n+2的常數項是不是簡單了些?若設計大些,如bn=3n-19還能做嗎?

設an=bm,得3m=2n+19,由二項式定理得

2n+19=(3-1)n+19=

比較上述3種視角,不難發現2、3適應范圍上受限制的程度較大,技術要求較高.而視角1從整體上在一個數列中尋找公共項的解題方法,這是解決此類問題的通法.

(作者單位：山東省鄒城市第一中學)