風浪破碎判據的實驗檢驗

楊景耀，鄒曉晨

（1.天津市靜海區第四中學，天津　301600；2.中國海洋大學海洋與大氣學院，山東　青島　266100）

風浪破碎判據的實驗檢驗

楊景耀1，鄒曉晨2

（1.天津市靜海區第四中學，天津301600；2.中國海洋大學海洋與大氣學院，山東青島266100）

利用已有風浪破碎實驗觀測數據檢驗了風浪破碎判據的可靠性。實驗測量了風浪波面位移的時間序列，并人工同步標記出破碎發生的時刻。研究了4種常用判據，包括波陡、瞬時波面斜率、波峰水質點水平速度與相速度之比，以及波峰水質點向下加速度與重力加速度之比。采用破碎判據對所測風浪序列中的破碎波進行識別，根據人工標記數量計算破碎率以確定破碎閾值。計算結果表明，幾何判斷閾值接近Stokes波極限值，而運動學和動力學判斷閾值則明顯偏離。進而檢驗了判據識別出的破碎波與人工標記破碎波的一致性。在達到破碎閾值的波中，約35%～55%與人工標記相對應，約有45%～65%的波，雖然滿足了閾值條件，卻并未發生破碎，說明風浪的破碎可能并非完全取決于其中任一判據所關注的波浪特征量。

海浪；波浪破碎；破碎判據

風浪破碎是一種常見而重要的海洋現象，是風浪能量耗散的主要機制（王偉，1990）。風浪的能量源于風場，耗散于破碎，總體上維持著動態的平衡。另外，風浪破碎過程中產生的氣泡、飛沫對海氣交換、海洋遙感等有重要影響。破碎判據是風浪破碎研究的關鍵問題之一（倪文勝等，2002），由于風浪破碎的復雜性，已提出的破碎判據仍有很大的不確定性（楊家軒等，2015）。

破碎判據一般可分為幾何判據、運動學判據和動力學判據3類。幾何判據通過波面的幾何特征進行破碎判別，其中最主要的是波陡判據（Stokes，1880），認為波陡超過某個閾值時發生破碎，即判據為：

其中g為重力加速度。另一個常用的幾何判據考察的是瞬時波面斜率（Longuet-Higgins et al，1977），可表示為瞬時垂向速度v與相速度c之比（Longuet-Higgins et al，1983），當滿足

其中H和λ分別代表波高和波長。對于實驗記錄的固定點波面位移時間序列，波長通常根據頻散關系由周期估算。對于深水波浪，利用頻散關系可將公式（1）化為：

時發生破碎，κ代表瞬時波面斜率閾值。運動學判據認為當波峰處水質點的水平速度u與相速度c之比超過某個閾值β，即滿足

時發生破碎。動力學判據認為當波峰處水質點向下加速度a與重力加速度g之比超過閾值γ時發生破碎，即：

1　實驗數據描述

本文使用的風浪數據來自類淑河（2010）的實驗。該實驗在中國海洋大學物理海洋實驗室的大型風-浪-流水槽中進行。水槽長65 m，寬1.2 m，高1.5 m。實驗水深0.7 m，對于實驗風浪波長的尺度可以近似為深水。實驗采用鉭絲測波儀（以下簡稱測波儀）測定固定點的波面位移，在水下放置多普勒流速測量儀同步測量三維流速。實驗過程中，借助與測波儀主機相連的電容器對破碎事件進行人工記錄。觀測者在鉭絲位置進行觀察，當觀察到破碎時扭動一次電容器旋鈕，記錄一個高電位信號。與此同時一臺錄像機對實驗波面進行全程錄像，以備后期對人工標記進行核對，以及對實驗效果進行評估。此破碎記錄由人工進行，產生的高電位信號與破碎發生的時間點之間難免存在偏差，但總體而言大部分破碎記錄仍是可靠的。在后期分析中進行破碎波判別時，該人工破碎記錄可以作為破碎發生的重要參照依據。

實驗在6.35、7、7.5、8、9 m·s-1共5個風速下進行，同時在3個風區處（分別為30.0m、34.2m、39.7 m）放置測波儀。在給定風速下，改變ADV的深度進行多次測量。每次測量持續560秒，共記錄15 000個波面位移數據，約14 000個ADV流速數據。

本實驗共獲得47組風浪數據。通過查看人工破碎記錄和實驗錄像，篩選出破碎顯著且錄像清晰的4類共15組數據用于本文研究。數據序號、實驗參數以及破碎特征見表1。

表1　實驗參數與破碎特征

2　數據濾波處理

圖1(a)是一段波面位移原始記錄。可以看到，在顯著波之上存在騎行的小波。

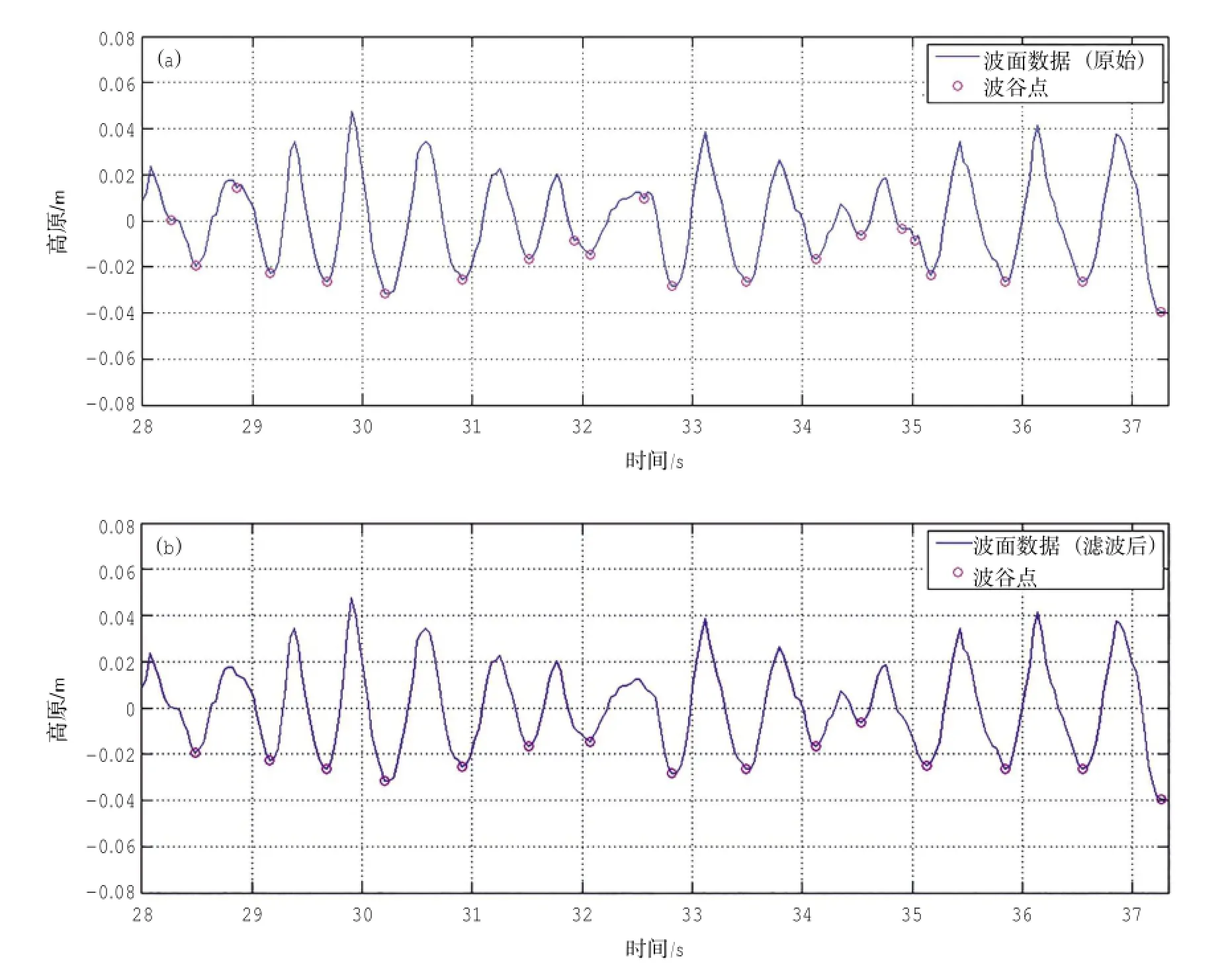
圖1 濾波效果圖

在進行破碎識別時，需要對每個顯著波逐個分析，計算其波陡、斜率等破碎判據考察的特征量（以下簡稱判據參量）。本文采用波谷法，定義兩個相鄰波谷之間的波面為一個單個波，騎行波的存在必然對單個波的劃分及判據參量的計算產生干擾。為避免這一干擾，本文首先對實驗數據進行濾波處理，對騎行波進行濾除。Banner（2002）提出一種濾除騎行波的方法（以下簡稱Banner02方法），其基本思路是將波列中的高頻波抹去，然后采用3次樣條插值方法進行補值。該方法既可以有效濾除騎行波，又能夠保持顯著波波形基本不受影響。本文采用Banner02方法進行濾波，主要步驟如下：

（1）找出波面上的波谷的位置，如圖1中的紫色圓圈所示；定義兩個相鄰波谷之間的波面為一個單個波，分別計算每個單個波的頻率。

（2）將所有單個波按頻率從大到小排序，篩選出頻率超過譜峰頻率1.9倍的波。

（3）對篩選出的高頻波逐一處理，先將其波面數據直接抹除，再通過對其前后1秒內的波面數據使用3次樣條插值進行補值。

（4）重復以上步驟，直至所有單個波頻率都超過譜峰頻率1.9倍。

波列經過濾波處理后，絕大多數騎行波已經被去除，但仍有少數振幅極小的干擾波存在。下一步我們依次抹去所有波高小于1 cm的波，采用線性插值進行補值。經過以上處理后，所得波面如圖1（b）所示。在圖1（b）中，采用波谷法可以識別出14個單個波，與直接觀察結果一致。

3　對各破碎判據的檢驗

本節使用經過濾波處理后的15組數據，對前文所述的4種破碎判據進行檢驗。首先計算每組數據中各單個波的判據參量，控制閾值的大小，使各判據所識別的破碎波總數達到人工破碎標記次數，從而確定每組數據所對應4種破碎閾值。各參量的具體計算方法見表2，破碎閾值計算結果見圖2（a）-（d），均值和標準差見表3。

從表3中可以看到，波陡和波面斜率的閾值觀測結果接近理論值，標準差也較小。Ochi等（1983）也觀測了波陡閾值，對于深水隨機波，得到α=0.125，低于理論值和本文觀測結果。表3中運動學判斷閾值觀測結果偏離Stokes波理論極限較大，更接近于Tulin等（2001）提出的新判據：，其中cg為群速。動力學閾值的觀測結果也明顯偏離理論值，已發表的動力學判斷閾值實驗結果較為分散。Snyder等（1983），Ochi等（1983）、Longuet-Higgins（1985）的觀測分別給出r=0.5、0.39和0.32，均低于本文結果。

表2　各參量計算方法

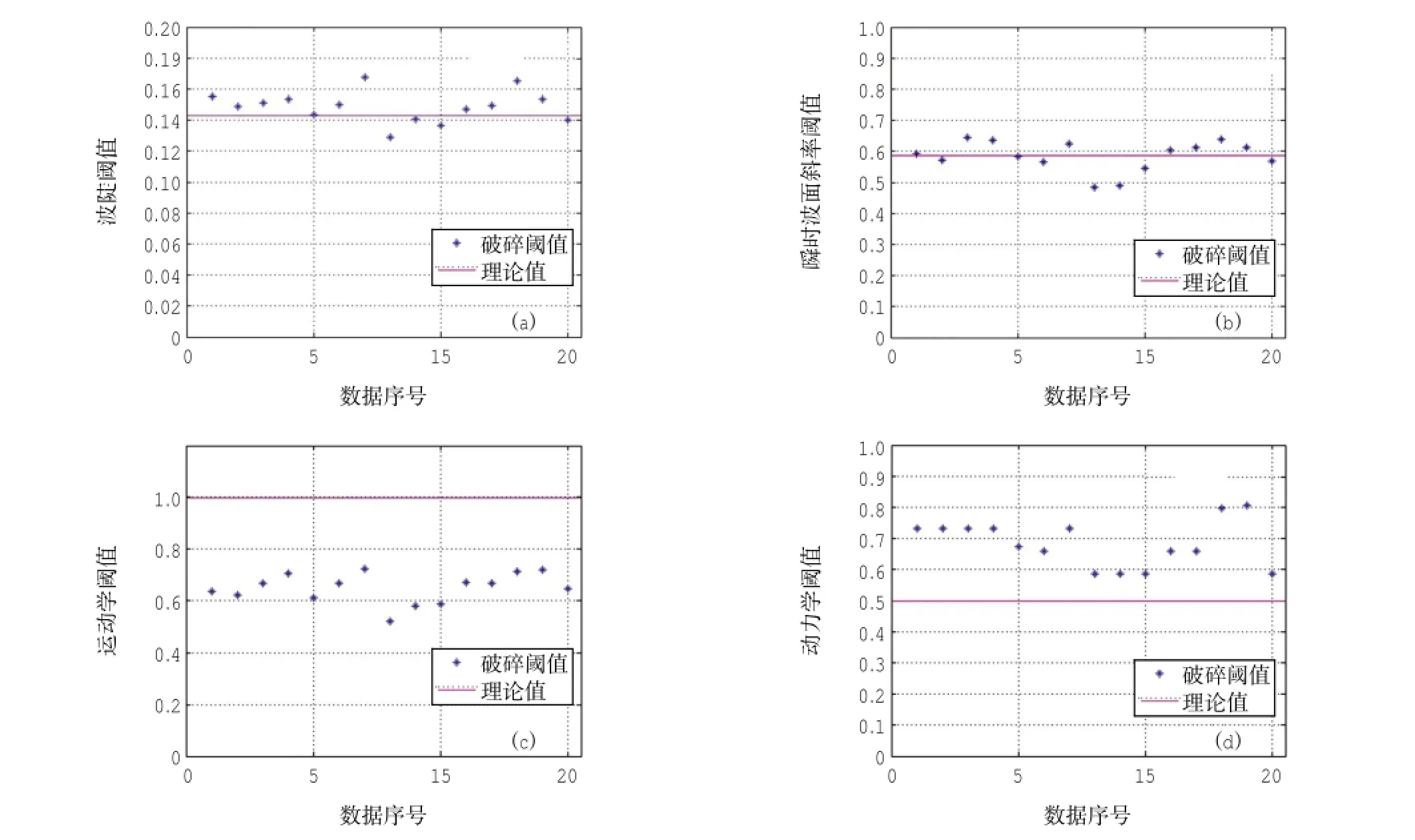
圖2　破碎閾值的計算結果

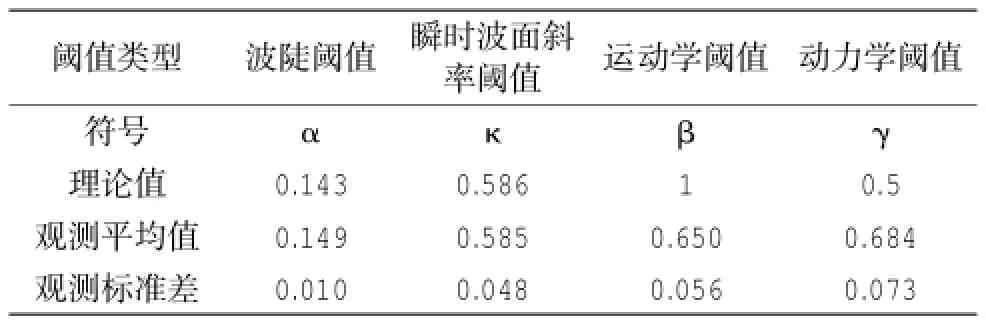
表3　破碎閾值理論值、觀測所得均值和標準差

為進一步考察破碎判據識別出的破碎波（以下簡稱識別破碎波）的可靠性，下面比較識別破碎波與含人工標記波的吻合程度。考慮到人工標記可能存在提前、延后等誤差，實驗中標記位置與人工觀察到的破碎波未必準確重合，給評價利用判據識別破碎的有效性帶來困難。在本文研究中我們對“含人工標記波”進行適當推廣，認為在標記點前后兩個波周期（約1 s）內的波為可能的含人工標記波。

圖3-圖6截取了一段波面作為破碎識別示例。每張圖分為3張字圖，其中下圖顯示了這段時間內人工破碎標記的位置；中圖為波面位移數據，其中識別破碎波標記為紅色；上圖中用“*”標記出了這段時間內所有識別破碎波的判據參量值分布，其中含人工標記的波標記為紅色。定義表征判據可靠性的指標如下：

A=滿足閾值且含標記的波總數/所有滿足閾值的波總數

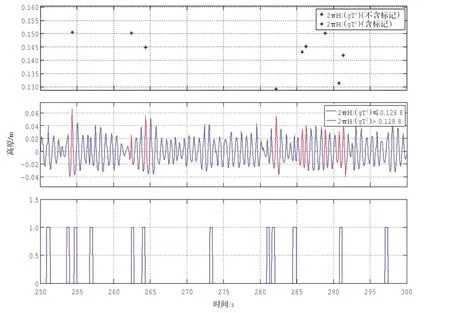
圖3　波陡判據可靠性示意圖

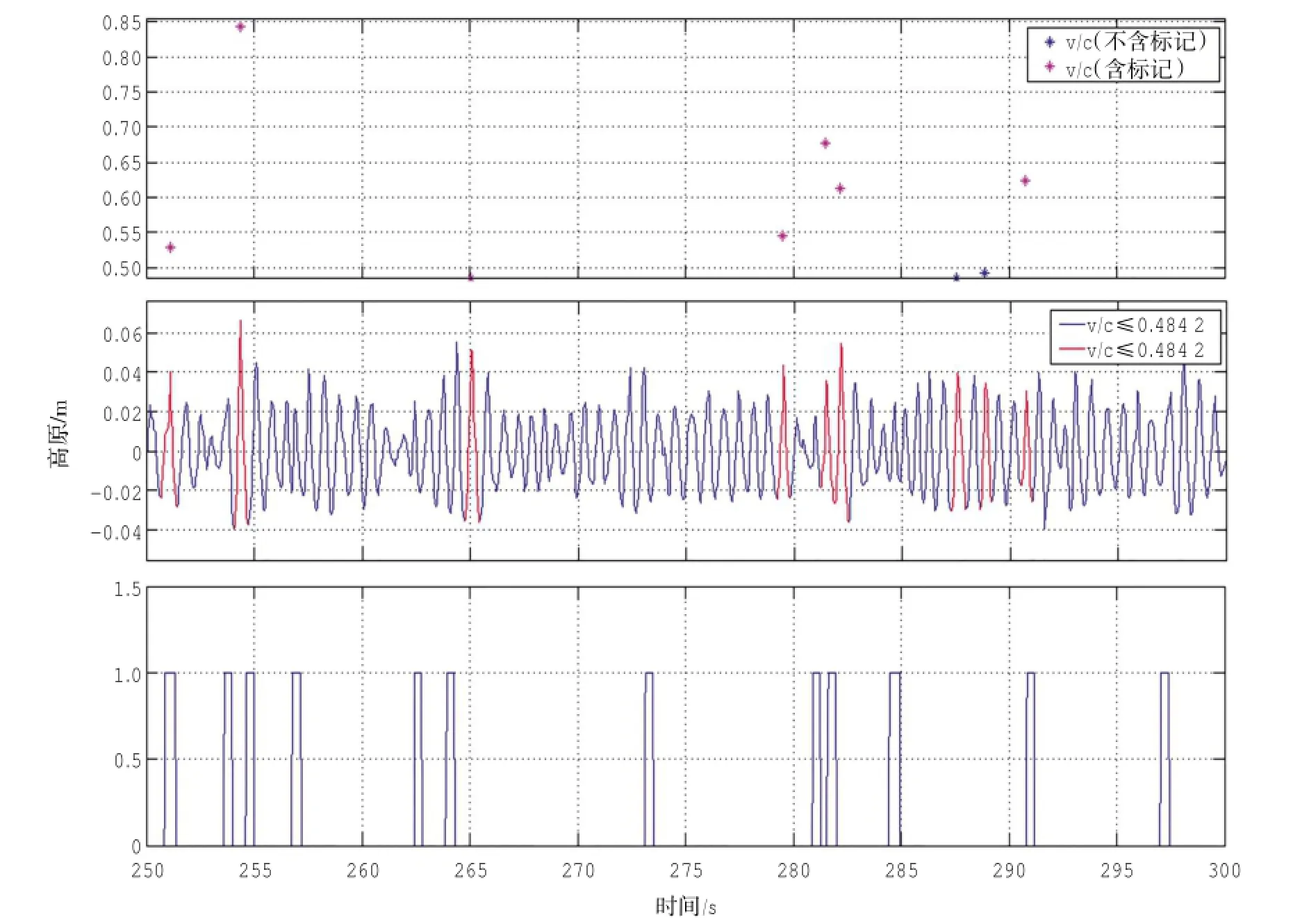
圖4　瞬時波面斜率判據可靠性示意圖

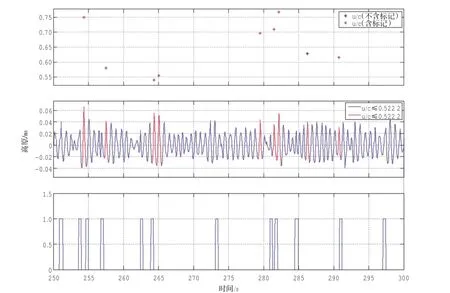
圖5　運動學判據可靠性示意圖

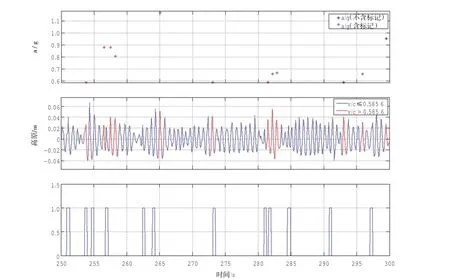
圖6　動力學判據可靠性示意圖

表4給出了全部15組數據中A的統計結果。

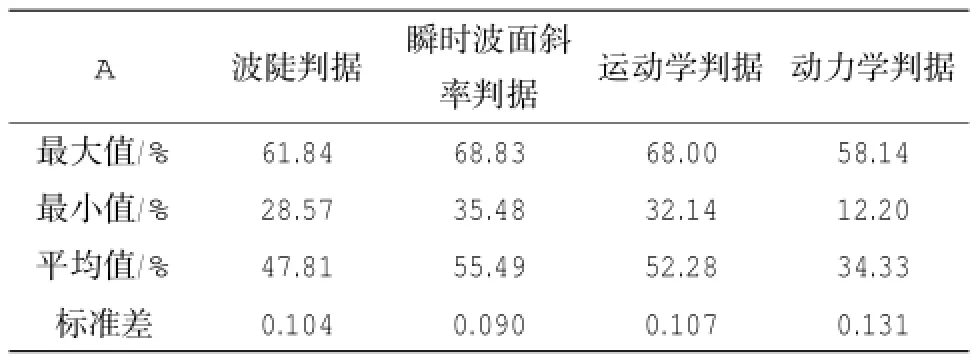
表4　4種判據可靠性計算結果

計算結果顯示，在所有滿足破碎閾值的波中，總體上約有35%～55%的波與人工標記相對應，其余45%～65%的波雖然滿足破碎閾值條件，卻可能并未發生破碎。對于同一個波，不同的破碎判據可能給出不同的判斷結果。

4　結論

本文采用波陡判據、瞬時波面斜率判據、運動學判據及動力學判據，對風浪數據進行破碎識別，依據實驗中人工觀察到的破碎率確定判斷閾值。計算結果表明，各組數據的判斷閾值隨著風速、風區的變化有小幅度的波動，但總體上始終穩定在平均值附近。其中波陡閾值、瞬時波面斜率閾值的平均值與Stokes、Longuet-Higgins等所給出的理論或數值研究結果近乎一致，運動學閾值普遍低于理論值，動力學閾值則高于理論值。基于以上破碎識別結果，本文分析了每組數據中判據識別破碎波與人工標記破碎波的一致性。結果顯示，總體上約有35%～55%的判據識別破碎波與人工標記相對應，其余45%～65%的波雖然滿足破碎閾值，卻可能并未發生破碎。風浪的破碎是一個復雜的物理過程，可能是多種波浪要素共同作用的結果，僅僅考察單一的波浪特征量進行破碎判別往往是不可靠的。

致謝：感謝中國海洋大學類淑河博士提供的實驗室風浪槽實驗數據。

Banner M L,Gemmrich J R,Farmer D M,2002.Multiscale measurements of ocean wave breaking probability.Journal of Physical Oceanography,32(12):3364-3375.

Longuet-Higgins M S,Cartwright D E,Smith N D,1963.Observations of the directional spectrum of sea waves using the motions of a floating buoy.

Longuet-Higgins M S,1969.On wave breaking and the equilibrium spectrum of wind-generated waves//Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences.The Royal Society,310(1501):151-159.

Longuet-Higgins M S,1974.Breaking waves in deep or shallow water// Proc.10th Conf.on Naval Hydrodynamics.597.

Longuet-Higgins M S,Fox M J H,1977.Theory of the almost-highest wave:theinner solution.Journal of FluidMechanics,80(4):721-741.

Longuet-Higgins M S,Smith N D,1983.Measurement of breaking waves by a surface jump meter.Journal of Geophysical Research:Oceans, 88(C14):9823-9831.

Longuet-Higgins M S,1985.Accelerations in steep gravity waves.Journal of physical oceanography,15(11):1570-1579.

Ochi M K,Tsai C H,1983.Prediction of occurrence of breaking waves in deep water.Journal of Physical Oceanography,13(11):2008-2019.

Snyder R L,Smith L,Kennedy R M,1983.On the formation of whitecaps by a threshold mechanism.Part III:Field experiment and comparison with theory.Journal of physical oceanography,13(8):1505-1518.

Stansell P,MacFarlane C,2002.Experimental investigation of wave breaking criteria based on wave phase speeds.Journal of physical oceanography,32(5):1269-1283.

Stokes G G,1880.Considerations relative to the greatest height of oscillatory irrotational waves which can be propagated without change of form.Mathematical and physical papers,1:225-228.

Tulin M P,Landrini M,2001.Breaking waves in the ocean and around ships//Twenty-Third Symposium on Naval Hydrodynamics.

Wu C H,Nepf H M,2002.Breaking criteria and energy losses for threedimensional wave breaking.Journal of Geophysical Research:O-ceans,107(C10).

類淑河,2010.風浪破碎的隨機性、非線性和能量耗散特征研究.中國海洋大學.

倪文勝,劉百橋,2002.近岸破碎波高概率分布研究.海洋通報,2:16-21.

王偉,1990.海洋白浪及其在海—氣交換過程中的作用.海洋通報,4: 87-93.

楊家軒,李訓強,朱首賢,等,2015.基于水槽實驗的近岸波浪破碎計算研究.海洋通報,1:45-51.

鄭桂珍,2003.風浪破碎統計特征及流對短波破碎影響研究.中國海洋大學.

（本文編輯：袁澤軼）

The laboratory investigation on the criterions for the wind wave breaking

YANG Jing-yao1,ZOU Xiao-chen2
（1.Jinghai District No.4 Middle School,Tianjin 301600,China;2.Collegeof Oceanic and Atmospheric Sciences, Ocean Universityof China,Qingdao 266100,China）

In this paper,the reliability of the criterions for the wave breaking onset is investigated with the available laboratory observations.In this experiment,the wave surface elevations as well as wave breaking onsets are recorded.The four commonly used criterions,wave steepness,the instantaneous inclination of wave surface,the ratio of the crest horizontal velocity to the wave's phase velocity,as well as the ratio of the crest downward acceleration to the gravitational acceleration are examined.These criterions are applied to time-runs of surface elevation to identify wave breaking onset.The thresholds of these criterions are determined from the measured breaking rate.The resulted geometric thresholds are very close to the Stokes wave limit,while that of the kinematic as well as dynamic ones deviate distinctly.Further,it is examined if the onsets of wave breaking recognized by the criterions are coincident with that recorded in the experiment.It is found that about 35%～ 55%of the wave breaking satisfy the criterions really occurred.In other words,about 45%～65%of the waves,whose criterion-concerned parameters are larger than the thresholds,have not break.It seems that anyone of the criteria may not sufficient for wave breaking onset.

ocean waves;wave breaking;breaking criterions

TV139.2

A

1001-6932（2016）05-0594-07

10.11840/j.issn.1001-6392.2016.05.014

2016-03-19；

2016-05-20

鄒曉晨（1993-），男，碩士，主要從事海浪、全球氣候變化研究。電子郵箱：zouxc1122@126.com