培養低學段學生數學思考能力初探
浙江紹興市上虞區華鎮小學(312365) 郭軍平
培養低學段學生數學思考能力初探
浙江紹興市上虞區華鎮小學(312365)郭軍平
數學思考是學生數學學習過程的基本活動,是獲取數學知識的必要途徑。從某種意義上來說,沒有數學思考就沒有數學學習。數學思考伴隨著數學學習的全過程,學生數學思考能力的培養要從小就開始。
低段教學數學思考能力培養
《義務教育數學課程標準》在“課程目標”中明確指出:“義務教育階段的數學學習要增強學生運用數學的思維方式進行思考,增強發現和提出問題的能力、分析和解決問題的能力。”由此可見,在小學數學教學中,教師須重視培養學生的數學思考能力。
所謂數學思考,就是在解決問題時,能夠自覺應用數學的知識、方法、思想和觀念去發現其中存在的數學現象和數學規律,從而解決問題的思想活動。
學生數學思考能力的培養應結合教學內容,從低年級開始就滲透在課堂教學各環節中。教師要重視創設氛圍、啟發思維、引導交流,持之以恒,才會取得成效。
一、營造和諧環境,助推積極思考
現代心理學認為:“兒童在無拘無束的活動中,在愉快和諧的、輕松的氣氛中,才能思維活躍,想象豐富,記憶力增強,相反的,在一個呆滯、具有種種約束的環境中,會思維堵塞,反應遲鈍,心境封閉,毫無創造力。”教師是課堂的組織者和引導者,教師在課堂中的一言一行、一舉一動都會顯著影響課堂的學習氛圍。要讓學生積極思考,教師就要創設師生平等的氛圍,為師生互動暢通渠道。教師還要學會欣賞學生的獨特感悟和多元見解,善于包容學生在學習過程中的“節外生枝”。
如教學“克和千克”后,教師組織學生應用克與千克去估一估物品的質量。由于生活經驗積累不足,學生對“1克有多重、1千克有多重”的感知還不深刻,因此當要判斷“1包薯片有多少克?幾個蘋果約種多少千克?10個雞蛋約有多少千克?估一估你的同桌大約有幾千克?”時,他們沒能做出精確的估計,有的學生估計的數與實際的質量相差很大。對于學生的錯誤猜測,教師沒有立即給出肯定或否定的評價,而是把所有的數據通過板書、投影呈現出來,讓學生針對自己估計的每個數據,說說估計的依據;引導學生運用剛才的經驗(以某一物品作為參照物),根據要估計的物品進行比較。至此,學生明確可以通過掂一掂,估計出物品的重量,同時明白估計要有理有據。有的學生明顯是亂猜的,因為讓他說依據時,他放棄了自己不正確的估計結果。有的學生雖然估計得不精確,但卻能說出估計的方法與依據,使其他學生受到啟發。在此基礎上,教師讓學生評價哪些數據比較精確或比較接近實際物品的重量。最后,教師讓學生用秤來鑒定。估得比較精確的學生很開心,沒有估計準的學生也能從中受益,學會怎樣估計才比較精確。
在這個過程中,教師沒有簡單地評判誰對誰錯,而是始終引領學生自主探索,深入思考。在這樣輕松、和諧的氛圍下,學生的數學猜想意識、猜想能力得到了提高。學生敢想、敢說、敢辯,獨立思考的“船”也隨之起航。
二、關注方法指導,學會數學思考
讓學生學會數學思考,是培養學生數學素養的核心內容。數學思考可溝通生活現實與數學之間的關系,使學生感受數學與生活之間的密切聯系,學會提出、分析和解決數學問題,從而積累數學活動經驗,體驗數學學習的快樂,進而提高數學素養。
如教學“用減法解決問題”時,教師用圖文結合的形式呈現了“有16人來踢球。現在來了9人。我們班踢進了4個。”這道題。這是解決問題教學中第一次出現有多余條件的題目,教師讓學生嘗試提出問題,再列式計算。在這個過程中,學生受加法解決問題經驗的影響,有的認為所有的條件都應該用上,所以提出的問題、列出的算式五花八門。
生1:一共踢進了幾個球?列式:9+4=13(人)。
生2:還要來幾人?列式:16-9-4=3(人)。
生3:還有幾人沒有來?列式:16-9=7(人)。
顯然,問題與列式解答相吻合的是第三個。教師抓住這一課堂生成性資源,引導學生分析、闡述自己思考和解決問題的過程。在此過程中,有的學生不會表達,有的表述不清楚,有的說與做存在矛盾。面對這些情況,教師讓學生充分闡明自己的想法,不管對還是錯,只要肯說就進行表揚。最后,教師引導學生從題目告訴我們什么、可以解決什么問題,或引導學生從要解決這個問題,必須要先知道什么進行思考,讓學生經歷數學思考的過程,提高學生提出問題、分析和解決問題的能力。
三、重視辨析交流,促進有序思考
知道了思考的方法,學生就會產生交流的愿望。教師應為學生創造交流的機會,讓他們有充足的時間去發現、去探討、去交流、去辨析、去評價,從中體會到數學思考的樂趣。
如教學“認識人民幣”時,教師設計了購物的游戲。游戲要求每人用2元2角買一件物品,不能找零。在學生獨立思考后,教師組織交流活動,要求學生說出自己用的是什么質地的人民幣(紙幣或硬幣)、用了哪些面值的人民幣,并要求學生認真傾聽,不隨意打斷他人的發言,思考發言學生的方法。在學生交流時,教師在黑板上分類記錄各種情況:
全部用紙幣的:2張1元紙幣、2張1角紙幣;2張1元紙幣、1張2角紙幣;1張1元紙幣、2張5角紙幣、2張1角的紙幣。
全部用硬幣的:2枚1元硬幣、2枚1角硬幣;4枚5角硬幣、2枚1角硬幣;1枚1元硬幣、2枚5角硬幣。
紙幣和硬幣混合的:1枚1元硬幣、1張1元紙幣、1張2角紙幣;2張1元紙幣、2枚1元硬幣;2張5角的紙幣、1枚1元硬幣、1張2角紙幣。
在學生發言完畢后,教師組織學生進行評價,并結合板書,引導學生學會全面、有條理地進行思考,從而促進學生更好地掌握解決問題的策略。
四、引導知識應用,培養獨立思考
數學思考作為過程性目標,實際上是讓學生經歷“做數學”的過程,讓學生在應用知識解決問題中經歷發現和提出問題、分析和解決問題的過程。這是喚起學生的好奇心,激發并維持學生主動學習數學的根本保證,是培養學生獨立思考的習慣和提高學生獨立思考能力的有效措施,也是培養學生實踐能力和創新意識的基本途徑。
如教學“小數的初步認識”時,教師這樣進行:
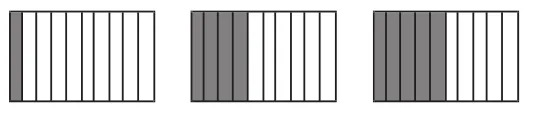
1.獨立思考,分別用分數和小數表示右圖中的陰影部分。
2.想一想,這個幾個分數和小數的單位是米或元時,它們各表示什么意思?
3.做了這道題,你有什么發現?
在教師的指導下,學生積極發言:
生1:1分米等于米,寫作小數是0.1米。
生2:4分米等于米,寫作小數是0.4米。
生3:6分米等于米,寫作小數是0.6米。
生4:我發現十分之幾這類分數可以用一位小數來表示。
生5:0.1是十分之一,所以百分之一可以用0.01來表示。
這樣,整個學習過程充滿獨立思考的空間,充分體現了每個學生獨特的思想和個性。學生在應用中不僅鞏固了所學知識,而且培養了獨立思考的習慣,提高了數學思考能力。
數學思考是數學學習的關鍵,也是數學教學的重要目標之一。學生數學思考能力的培養,應伴隨著數學學習的全過程。教師要在數學課堂中激發學生學習數學的興趣,引發學生積極思考,使之養成良好的思考習慣,掌握數學基本技能,感悟數學思想方法,積累活動經驗,提高數學思考能力。
(責編吳美玲)
G623.5
A
1007-9068(2016)29-071

