選例題要“一題多解” 做習題求“多題一解”——談畢業總復習階段“組合圖形的面積計算”的復習策略
浙江杭州市蕭山區樓塔鎮巖山中心小學(310000) 章中其
選例題要“一題多解”做習題求“多題一解”——談畢業總復習階段“組合圖形的面積計算”的復習策略
浙江杭州市蕭山區樓塔鎮巖山中心小學(310000)章中其
教師應摒棄以往“就題論題”的復習方法,引導學生把組合圖形的面積計算歸入知識系統后進行深入的探究,使學生體會到“合并求和”“去空求差”的數學思想方法,促進學生思維的發展。
一題多解多題一解合并求和去空求差思想方法
在課堂教學中,為了開拓學生的解題思路,培養和提高學生思維的廣闊性、靈活性,教師往往會采用“一題多解”的例題。“一題多解”的講解和訓練,不僅可以使師生加深對題旨的理解,而且可以促進學生明晰題中的數量關系,尋求到更合理、更簡捷的解題方法。如在畢業總復習階段復習“組合圖形的面積計算”時,我按照傳統的“一題多解”的方法,讓學生自我總結“萬變不離其宗”的思想方法,變“一題多解”為“多題一解”,使學生的解題能力得到提高。
一、選例題時要“一題多解”,使學生掌握思想方法
羅增儒認為:“分析典型例題的解題過程是學會解題的有效途徑,至少在沒有找到更好的途徑之前,這是一個無以替代的好主意。”因此,在畢業班總復習階段復習“組合圖形的面積計算”時,我采用不同的方法分割圖形,使學生在“一題多解”中自主歸納自己的解題策略,反思正誤、總結經驗,領悟和掌握解題的思想方法。
例:如右圖,算出圖形陰影部分的面積。
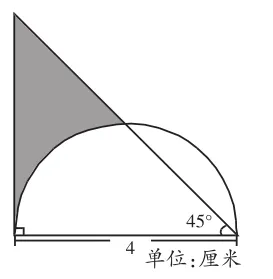
在動手解題前,對圖形進行仔細的觀察和初步的分析是十分必要的,有利于我們進一步分析題意、確定思維方法和找到解題路徑。題中的圖形由一個三角形和一個半圓組成,陰影部分由三角形的兩邊和半圓周的一部分圍成,這個三角形的一個角是直角,一個銳角是45°,由“三角形內角和等于180°”可以求出另一個銳角的度數,說明這個三角形是等腰直角三角形。

解法1:如右圖,很明顯,陰影部分面積等于這個直角三角形面積減去半圓在三角形內的部分面積,因為兩直角邊是已知的,容易求得直角三角形的面積,現在關鍵在于求出半圓在直角三角形內部分的面積。為此目的,可以通過圓心和半圓周與直角三角形斜邊的交點畫一條輔助線,這樣就把半圓在三角形內部的部分分割成兩部分,即這個圓的和一個小直角三角形,然后在圖上分別用Ⅰ和Ⅱ來表示,于是問題得到解決。


解法3:如右圖,連接兩點間的線段,可以看出這條線段正好把這個直角三角形平均分成了兩部分(想一想,為什么),陰影部分的面積正好可以由這樣分得的直角三角形的一半減去弓形面積求出,這里弓形面積顯然和解法2中的弓形面積是相等的。這個分析過程可用下面的示意圖表示:
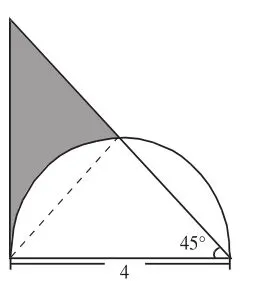

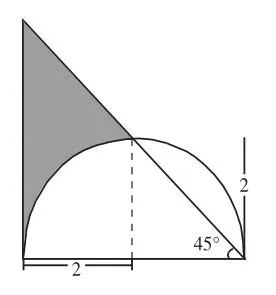
解法4:如右圖,與解法1相同,把圓心和三角形斜邊與圓周的交點連接起來,則這條線段一定平行于這個直角三角形的一條直角邊,這樣就得到了一個梯形,梯形的上底是圓的半徑,也就是這個直角三角形直角邊(即圓的直徑)的一半,下底是這個直角三角形的一條直角邊,高也是圓的半徑,所以陰影部分的面積就是這個梯形的面積減去這個圓的這個分析過程可以用下圖來表示

縱觀以上四種不同的解法,讓學生一邊看圖示,一邊總結,使學生首先領悟到無論哪一種解法都是“大圖形”減去“小圖形”。然后我出示以下兩個圖形,讓學生明確其一、其二都屬于組合圖形的面積計算,其一是“圖形加法”,用“合并求和”解決;其二是“圖形減法”,一般求陰影部分的面積用“去空求差”計算。

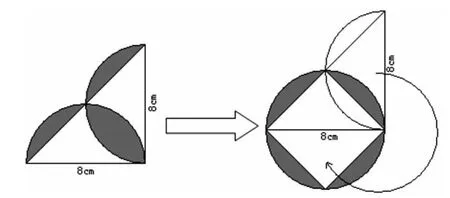
此外,組合圖形的面積計算有時也會用以下兩種方法解決:一是平移轉換。在計算陰影部分面積時,可以用移動變換圖形的方法求解。如右圖,通過平移,使我們明了陰影部分面積占正方形面積的二是旋轉變換,在看圖計算中應用比較廣泛。如下圖,通過旋轉陰影部分,使我們的解題思路豁然開朗。

二、做習題時求“多題一解”,促進學生自主掌握解法
我教畢業班已有十多屆,以往喜歡在畢業總復習階段尋找幾張練習卷,讓學生重復訓練《單元卷》《習題卷》,因涉及圖形的種類比較多,所以學生的訓練量比較大,情緒比較抵觸,效果也不明顯。近幾年,我摒棄以往重復、低層次練習的做法,選用經典例題,通過歸類訓練,讓學生自悟數學思想方法,其效果的確比較理想。
例如,在進行“一題多解”的經典例題教學后,我出示以下三組練習,讓學生能獨立解決的先獨立解決,但解決前要說說解決問題的策略是什么,如有什么疑問可以向同桌請教或與同組成員進行討論交流。
第一組:求下列圖形中陰影部分的面積。(單位:厘米)

本題組訓練,涉及的圖形幾乎包含了小學階段所有的平面圖形,由于圖形的數據比較簡單,且學生對于每一個圖形的計算公式均已牢記,所以學生列式計算的正確率達到100%。訓練后得出結論:原來這些題的解題策略都是“大圖形減去小圖形”(即‘去空求差’),關鍵是要明確求陰影部分的面積時,主要是由哪幾個基本圖形去減。
第二組:求下列圖形中陰影部分的面積。(單位:分米)

本題組訓練,學生單獨解決的錯誤率比較高:圖①的主要問題是受例題的負遷移影響,部分學生計算時漏掉了弓形的面積,部分學生按照例題的解決方法來做,算式比較長,計算容易出現錯誤;圖②的主要問題是一部分學生看到圖形比較復雜,一時找不到方法解決。但在訓練過程中,有相當一部分學生利用旋轉和翻轉的方法,輕松、快速地解決問題,并且發現了圖①和圖②之間的聯系(一分為二)與區別(拼成了平行四邊形或長方形,計算更簡單)。通過交流反饋,學生恍然大悟——原來“去空求差”中可以利用平移、旋轉等方法使解題策略更簡單,感受到了數學思想方法的魅力。
第三組:
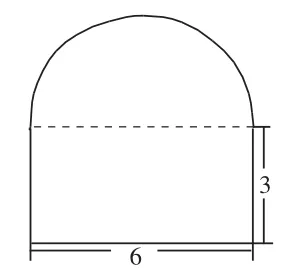
①如圖A,求圖形的面積(單位:厘米)。
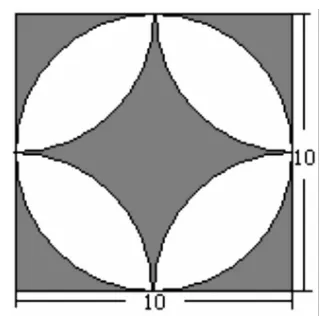
②如圖B,求陰影部分的面積和周長(單位:厘米)。
本題組訓練,圖①的難度不大,主要涉及“合并求和”的思想方法,學生都能夠掌握;圖②涉及周長的概念,學生對陰影部分的周長概念模糊,不清楚該圖形的周長應該包括哪幾部分,有些學生則漏掉了圓的周長部分。而且,圖B的面積部分更復雜,若是按照常規方法來解決,計算會很復雜,但學生的列式正確率還是比較高的。通過交流反饋,學生對于圖B的解題策略很令人欣慰:其一,周長采用類似于圖A面積計算“合并求和”的策略,用“正方形的周長+圓的周長×2”來解決;其二,計算面積的解決方案就更精彩了,特別是有學生利用“正方形內最大圓占其面積的78.5%,剩余部分占21.5%”的規律來解決問題,令人既意外又開心。
圖A
圖B
科學哲學家庫恩認為:“學生是通過范例、習題等來掌握一門科學知識及其方法的,沒有范例,科學知識就不能清楚地表達出來,也無法為人們所掌握;沒有范例,人們也無法按照該門科學的要求去解決任何問題,數學也不例外。”因此,教師應摒棄以往“就題論題”的復習方法,引導學生把組合圖形的面積計算歸入知識系統后進行深入的探究,使學生體會到“合并求和”“去空求差”的數學思想方法,促進學生思維的發展。
(責編藍天)
G623.5
A
1007-9068(2016)29-026

