數理統計直觀教學的實驗設計與R程序實現

呂書龍， 劉文麗， 梁飛豹， 葉福玲

(福州大學 數學與計算機科學學院， 福建 福州　350116)

?

數理統計直觀教學的實驗設計與R程序實現

呂書龍， 劉文麗， 梁飛豹， 葉福玲

(福州大學 數學與計算機科學學院， 福建 福州350116)

針對數理統計中關于格列汶科定理、正態抽樣定理、點估計和區間估計在教學中的常見疑惑和問題進行討論與分析，通過實驗設計和R程序，以圖形方式加以直觀解決。該實驗設計一方面促進了學生對于數理統計理論與方法的理解、提升了教學效果，另一方面也為R軟件在教學上的應用提供一種思路。

實驗設計； R軟件； 數理統計； 直觀教學

數理統計獨特的思維方式、抽象的理論、多學科知識的融合和豐富的應用，使得學生在學習這門課程時存在著一定的困難[1]。數理統計教學的重點和難點在于如何把統計思想和統計方法闡述清楚，并將其應用到實際問題中，這一點在文獻[2-3]中有充分闡述。關于統計思想和方法論的教育，有很多學者發表了富有建設性的觀點，例如在教學中充分利用統計軟件[4]和仿真技術[5]，強化實驗教學[6]和設計性實驗[7-10]等。

本文借助R軟件強大的隨機模擬和繪圖功能[11]，針對數理統計教學中的疑難點，特別是對抽象的統計思想及原理，提出以實驗設計和圖形展示為主的直觀教學[12]模式，并以格列汶科定理、正態抽樣定理、點估計和區間估計的教學為例予以說明，目的是促進學生對課程內容的理解、提升教學效果，同時也嘗試培養學生的動手能力和創新應用能力。

1　格列汶科定理

設總體X的分布函數為F(x)，經驗分布函數為Fn(x)，則格列汶科定理可以描述成：

ns=c(30,50,100,200,400,500,800,1000)

y=seq(-4,4,by=0.001)

par(mfrow=c(2,4))

for (i in 1:8)

{plot(y, pnorm(y), type=′l′)

x=rnorm(ns[i])

lines(ecdf(x),cex=0.1)

text(-2.5,0.9,paste(′n=′,ns[i],sep=″′))

}

由圖1可粗略地看出，經驗分布函數要較好地逼近分布函數，n不能太小。當n為100和200時，從逼近程度看還是可以接受的；若想得到更好的逼近效果，n應不小于200。從教學角度講，直觀地展示定理結論是一方面，而了解定理的適用條件也是必要的。因此建議把尋找滿足某個逼近標準的最小樣本容量n的問題作為課外探索題，這樣更能增強學生對定理的理解程度。

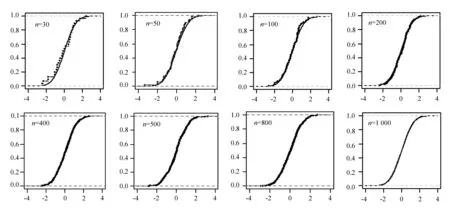
圖1　經驗分布函數與分布函數比較

該定理的特別之處在于它研究的是|Fn(x)-F(x)|變量的偏差上界，雖然理論上已經對它的分布做了證明并能給出相應的概率，但還是沒給出n多大時才能較可靠地使用這個定理。不妨通過抽樣模擬來刻畫這個過程：以標準正態分布為例，讓樣本容量n從10變到500，對每個n，模擬100次得到100個樣本，并計算每個樣本的經驗分布函數與分布函數偏差的最大值，再計算最大值序列的極差，最后畫極差圖(見圖2)，R程序如下：

getmax=function(size,n)

{a=numeric(size)

for(i in 1:size){

x=rnorm(n); tmp=ks.test(x,′pnorm′)

a[i]=tmp$statistic} #利用ks檢驗得到最大偏差

return(a)

}

n=seq(10,500,by=10);nlen=length(ns)

mat=matrix(0,nrow=2,ncol=nlen)

for(i in 1:nlen) mat[,i]=range(getmax(100, n[i]))

plot(n, mat[1,], ylim=c(0,max(mat[2,])+0.01), cex=0.5)

points(n, mat[2,], cex=0.5)

for(i in 1:nlen) lines(c(n[i], n[i]), mat[,i])

從圖2可直觀看出，極差變化先隨n的變大快速變窄，當n≈200時，極差變化趨于平緩，之后基本保持不變。可見n≥200是個不錯的選擇，這也進一步肯定了圖1的結論。

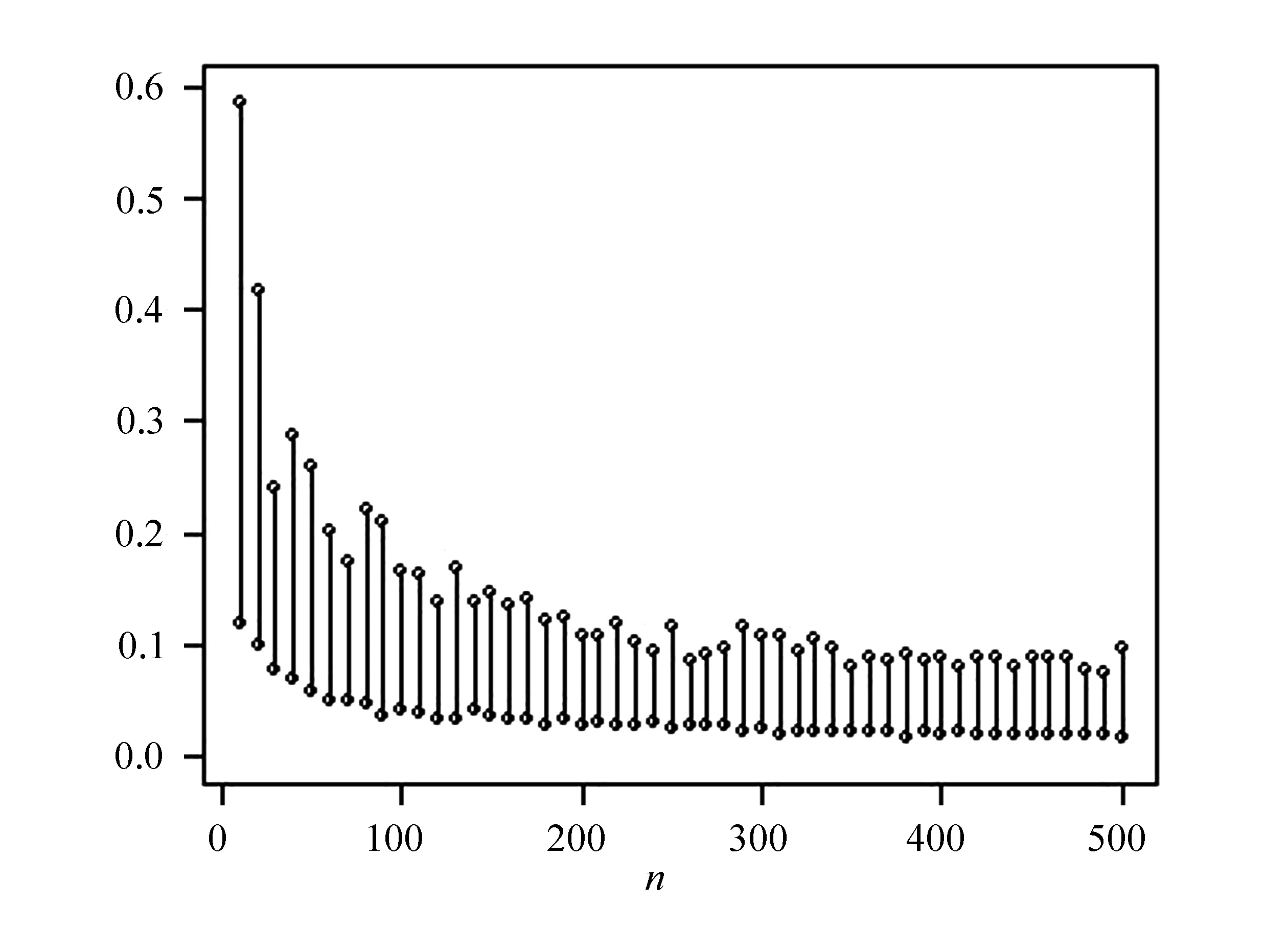
圖2　最大偏差的極差圖

2　正態抽樣定理的一個直觀描述

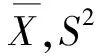
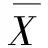
n=100;times=1000;mean=1;sd=2;N1=99; N2=100;sn=numeric(times);tmp=(n-1)/(sd^2)

for(i in 1:times){

set.seed(i); x=rnorm(n,mean,sd);sn[i]=tmp*var(x)}

plot(ecdf(sn),verticals=TRUE,do.point=FALSE)

nx=seq(70,140,by=1)

lines(nx,pchisq(nx,N1),lty=2,lwd=2)

lines(nx,pchisq(nx,N2),lty=4)

legend(130,0.8,c(′經驗分布函數′,′chisq(99)′, ′chisq(100)′),lty=c(1,2,4), cex=0.75, lwd=c(1,2,1)

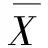
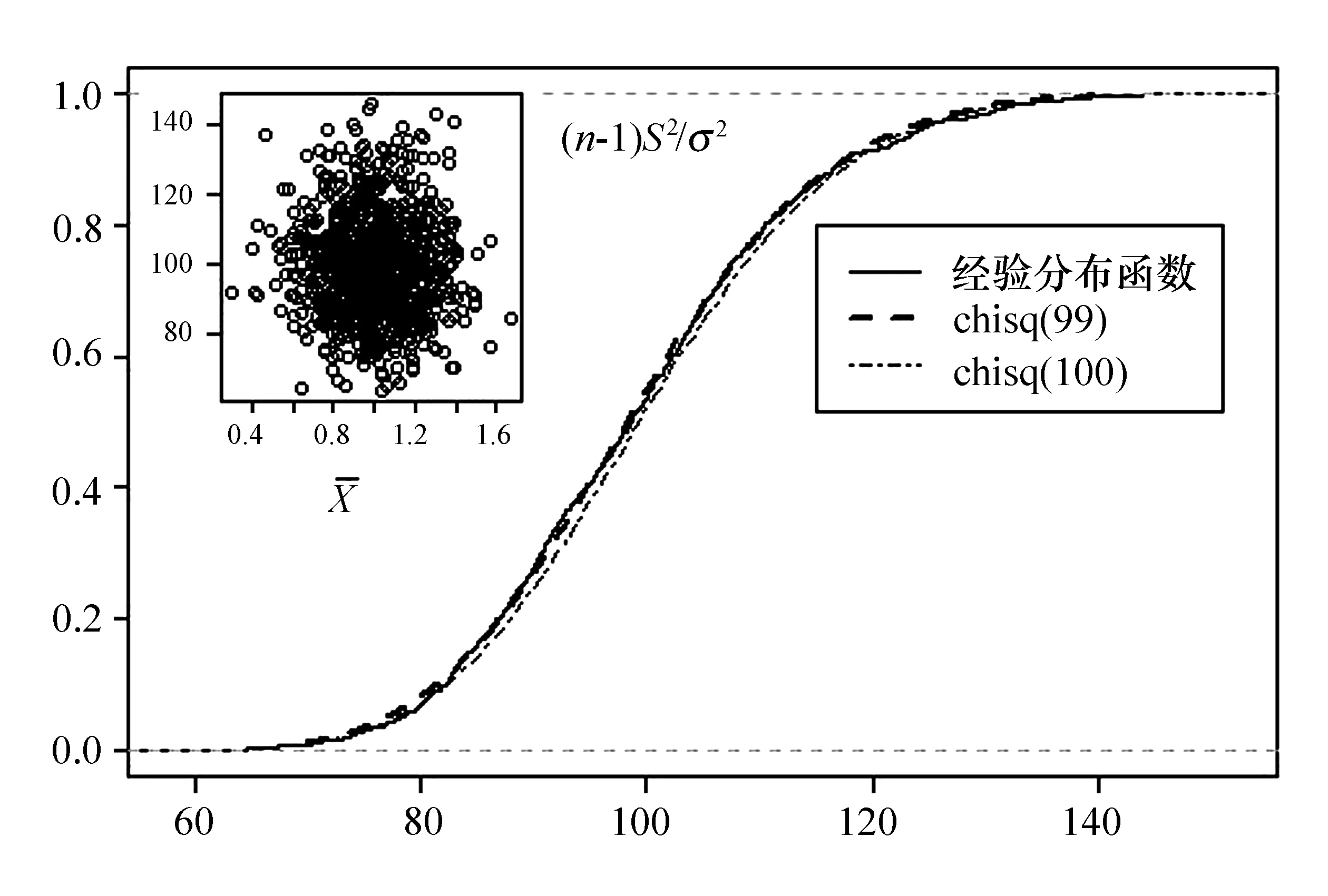
圖3　(n-1)S2/σ2與χ2(99)，χ2(100)的比較

3　矩估計和極大似然估計的比較

矩估計方法簡單易用，但也有明顯的缺點，例如估計量表示不唯一、樣本信息利用不充分等。極大似然估計能克服矩估計的缺點，在實際中應用更廣泛。相信學生并不喜歡這樣的比較，而若能配置一個實例進行直觀展示，將會收到良好的教學效果。實驗設計為：從總體U(0,θ) (不妨設θ=10)中抽取容量n=20的一個樣本，計算θ的矩估計和極大似然估計，重復40次后繪制估計值(見圖4)，R程序如下：

#est1和est2 分別記錄每次的矩估計和極大似然估計值

n=20; times=40;est1=rep(0,m);est2=rep(0,m)

for(i in 1:times)

{ x=runif(n,0,10); est1[i]=2*mean(x);est2[i]=max(x)}

plot(1:m,est1,type=″l″, ylim=c(min(c(est1,est2))-0.1,max(c(est1,est2))+0.1) )

points(1:m,est1); lines(1:m,est2)

points(1:m,est2,pch=16);abline(h=10)#畫出真值直線

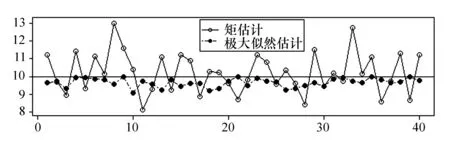
圖4　均勻分布參數兩種估計的比較

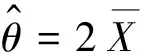
4　參數的置信區間

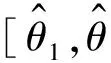
給定置信度1-α，從正態總體中抽取50個隨機數，計算均值的置信區間；重復該過程N次(N=100)得到N個置信區間并繪制成空心端點垂線圖，然后繪制真值水平線，將沒被水平線穿過的區間用實心端點表示(見圖5)，R程序如下：

Confidence = function(n=50,times=100,mu=0,sd=1,alpha=0.05)

{interval=matrix(0,nrow=times, ncol=2)

for(i in 1:times){

x=rnorm(n,mu,sd);mx=mean(x)

u_half=qnorm(1-alpha/2,mu,sd)*sd/sqrt(n)

interval[i,]=c(mx-u_half,mx+u_half)}

miny=min(interval)-0.01;maxy=max(interval)+0.01

plot(1:times,seq(miny,maxy,length=times),type=′n′)

abline(h=mu)

for(i in 1:times){

if(prod(interval[i,]-mu)>0) points(c(i,i),interval[i,],pch=16)

else points(c(i,i),interval[i,],pch=1)

lines(c(i,i),interval[i,])}

}

Cofidence(50,100,0,1,0.05)

在置信度為95%的前提下，不包含參數真值的區間數不超過5次，從圖5可看出：該模擬有3次不包含真值，符合這個要求。顯然Nα只是不包含真值這個事件的頻數，受樣本的隨機波動影響，不具有嚴格的相等性約束。

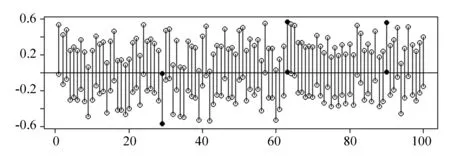
圖5　置信度的一次模擬圖形

5　關于最短雙側置信區間的討論

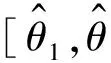
ns=c(2,4,6,8,10,15,20,25,30)

alpha=0.05

par(mfrow=c(3,3))

for(n in ns)

{ mat=matrix(0,nrow=200,ncol=2)

standar=c(qchisq(alpha/2,n),qchisq(1-alpha/2,n))

mat[,1]=seq(standar[1]/20,standar[1]*1.2,length=200)

for(i in 1:200)

{ p=pchisq(mat[i,1],n)

mat[i,2]=qchisq(p+1-alpha,n)

}

plot(mat[,2]-mat[,1],type=′l′,xlab=paste(′n=′,n,sep=′′),ylab=′區間長度′)

abline(h=standar[2]-standar[1])

}

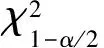
上述過程直觀地展示了標準置信區間的漸進收斂性，是對區間估計教學的直觀補充，更是對習慣性使用標準置信區間的一種直觀解釋。此外，還可以將尋找最短置信區間留作課后探索性實驗題，讓學生探討置信區間的常規求解方法。

從圖6還看到：當自由度n≥20時，標準置信區間長度已經很接近最短區間長度。此處n≥20可作為區間估計實際應用的一種參考；其次也說明此時χ2(n)的分布已經很接近對稱型分布了。實際上，從χ2(n)的構造定義知其滿足獨立同分布中心極限定理的條件，于是容易推出χ2(n)的漸進分布為正態分布N(n,2n)，而正態分布就是對稱型分布，這就不難解釋上述的結論。以下給出不同自由度下χ2(n)的密度函數比較(見圖7)，R程序如下：

ns=seq(10,40,by=10)

par(mfrow=c(1,4))

for(n in ns)

{

x=seq(0.01,n*2,by=0.1)

plot(x,dchisq(x,n),type=′l′,xlab=paste(′n=′,n,sep=″))

}

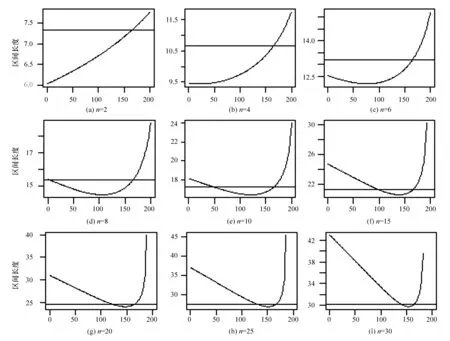
圖6　χ2(n)不同自由度下置信區間的比較

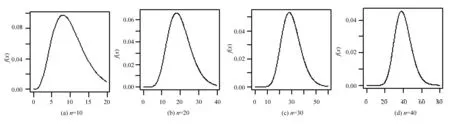
圖7　χ2(n)的密度函數

6　結語

在數理統計教學中引入R統計軟件是一種趨勢，利用R強大的隨機模擬和繪圖功能，通過設計合理的實驗和編寫程序，可將數理統計的概念、理論和方法演繹得更生動、更直觀。這種直觀的處理方式可增強學生對課程知識的理解，也能提升課程內容的趣味性和實用性，更能激發學生的探索興趣和創造性。現在已有越來越多的學生主動關注利用R軟件和統計方法去解決實際的問題。

References)

[1] 王巖.工科專業數理統計實驗教學的實踐探索[J].數學教育學報,2007,16(3):95-98.

[2] 劉超,吳喜之.統計教學面臨的挑戰[J].統計研究,2012,29(2):105-108.

[3] 史書良.統計思想教育重于統計方法教育[J].中國統計,2008(2):56-57.

[4] 吉祖勤,蔡長安.NS2仿真技術在網絡實驗教學中的應用[J].實驗技術與管理,2011，28(12):96-99.

[5] 關彥輝.R軟件在《概率統計》教學中的應用[J].現代計算機:專業版,2009(12):87-90.

[6] 顧光同,張香云,徐光輝.統計實驗寓于概率統計教學的探索與實踐[J].統計與決策,2007(21):165-167.

[7] 陳懷俠,蔡火操,黃建林，等.設計性實驗教學的實踐與思考[J].實驗技術與管理2006,23(11):105-107.

[8] 郝小江,繆志農,黃昆.基于DSP的數字信號處理實驗設計[J].2012,29(2):44-47.

[9] Robert C P, Casella G. Monte Carlo Statistical Methods[M].New York:Springer,2004.

[10] Efron B, Rogosa D, Tibshiran R. Resampling Methods of Estimation[M]//International Encyclopedia of the Social & Behavioral Sciences.2001:13216-13220.

[11] 薛毅,陳立萍.統計建模與R軟件[M].北京：清華大學出版社,2007.

[12] 呂書龍,劉文麗,涂淑珍,等.概率論直觀教學與R統計軟件實現的探索[J].龍巖學院學報,2015,33(5):98-101.

Experimental design and R program realization of intuitive teaching of mathematical statistics

Lü Shulong, Liu Wenli , Liang Feibao, Ye Fuling

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou 350116. China)

This paper discusses the doubts and problems of the Glivenko-Cantelli theorem, sampling theory, point estimation and interval estimation in mathematical statistics teaching, and puts forward the experimental design and R programs to graphically solve them directly. It not only promotes the students’ understanding of mathematical statistics and improves the teaching effects, but also enhances the application of R software in the teaching fields.

experimental design; R software; mathematical statistics; intuitive teaching

10.16791/j.cnki.sjg.2016.10.036

2016-03-29

福建省本科高校教育教學改革研究項目(JAS151395)；福州大學研究生優質課程建設項目(52004634,52004612)；福州大學高等教育教學改革工程(52001024,52001069)

呂書龍(1977—)，男，福建閩侯，碩士，副教授，主要研究方向為概率統計、統計計算和統計應用.E-mail：wujispace@126.com

O212.1；TP311

A

1002-4956(2016)10-0142-05