巖土工程可靠性分析方法及應用發(fā)展現(xiàn)狀

張啟兵　（安徽省水利水電勘測設計院勘測分院，安徽　蚌埠　233000）

巖土工程可靠性分析方法及應用發(fā)展現(xiàn)狀

張啟兵（安徽省水利水電勘測設計院勘測分院，安徽蚌埠233000）

可靠性分析已經(jīng)比較成熟地應用于工程結構設計當中，由于巖土工程自身的特點，巖土工程可靠性分析的應用發(fā)展較為緩慢。文章簡單介紹了可靠度設計標準、失效概率、可靠指標以及可靠指標的計算方法，分析了巖土工程存在的不確定性特點，并指出我國巖土工程可靠性分析的發(fā)展現(xiàn)狀和存在的問題。

巖土工程；失效概率；可靠度；一次二階矩方法；正態(tài)分布

0　引言

可靠性基礎理論研究已有較長時間，早在上世紀20年代，國際上就已經(jīng)開始了這方面的研究；二戰(zhàn)后可靠性理論得到了進一步完善和發(fā)展。早期主要應用于軍事和工業(yè)生產(chǎn)，后來逐步應用于工程領域，在土木工程結構方面的應用也較早。

工程結構的可靠性是指安全性、適用性和耐久性的總稱。工程結構在規(guī)定的時間內(nèi)，在規(guī)定的條件下，若其安全性、適用性和耐久性均得到保證，則表明工程結構是可靠的，完成預定功能的概率稱為工程結構的可靠度。本文對可靠性分析基本概念的闡述和計算方法介紹都基于土木工程結構設計。

1　可靠度設計水準

工程結構設計方法可分為經(jīng)驗安全系數(shù)法和概率設計法。經(jīng)驗安全系數(shù)法是將影響工程結構安全的各種參數(shù)按經(jīng)驗取值，一般為平均值或標準值，考慮這些參數(shù)的變異性對安全性的影響。概率設計法將影響工程結構安全的各種參數(shù)作為隨機變量，用概率論和統(tǒng)計學來分析參數(shù)，或用可靠度分析工程結構在使用期限內(nèi)滿足基本功能要求的概率。現(xiàn)在工程結構設計領域已逐步由經(jīng)驗安全系數(shù)法向概率設計法轉變。國際上將可靠度設計分為三個水準，水準Ⅰ、水準Ⅱ和水準Ⅲ。

水準Ⅰ也稱半概率設計法，在荷載和材料強度上考慮了概率原則，不從結構的整體性出發(fā)考慮工程結構的可靠度，無法確定工程結構的失效概率，且各分項安全系數(shù)主要根據(jù)工程經(jīng)驗確定。

水準Ⅱ也稱近似概率設計法，運用了概率論和數(shù)理統(tǒng)計的方法，對“可靠概率”做出較為近似的相對估計，但該方法只是一各近似的概率方法，是目前國際上已經(jīng)進入實用階段的概率設計方法。

水準Ⅲ也稱全概率設計法，將影響工程結構可靠度的所有因素用隨機變量的概率模型描述，還考慮了時間因素，以失效概率作為工程結構可靠度的直接度量，是一種完全的、真正的概率設計方法。該方法要達到實用階段還要很長時間。

2　可靠度與失效概率

可靠度是評價工程可靠性的指標，常用Pr表示，若在規(guī)定的時間和條件下，結構不能完成預定的功能，相應的概率則稱為失效概率，用Pf表示。

假定抗力R和荷載S為兩個獨立的隨機變量，服從某種分布形式，且均為連續(xù)型隨機變量，其概率密度函數(shù)分別為fs（S）和fR（R），那么當R小于S時則認為發(fā)生失效。可用下式表示：

用概率理論來研究工程結構的可靠性，綜合考慮投資風險和社會、經(jīng)濟后果，當失效概率小到人們可以接受的程度，就認為結構是可靠的，這是概率極限狀態(tài)設計的基本思想。

3　可靠指標

3.1可靠指標的表示方法

工程中引用可靠指標的概念，設抗力R和荷載S都服從正態(tài)分布，其平均值和標準差分別為μR、μS和σR、σS，且極限狀態(tài)方程為Z=R-S=0。則Z也服從正態(tài)分布。有：

將的正態(tài)分布N（μZ，σZ）轉化為標準正態(tài)分布N（0，1），引入標準化隨機變量 t（μt=0，σt=1），即，得出：

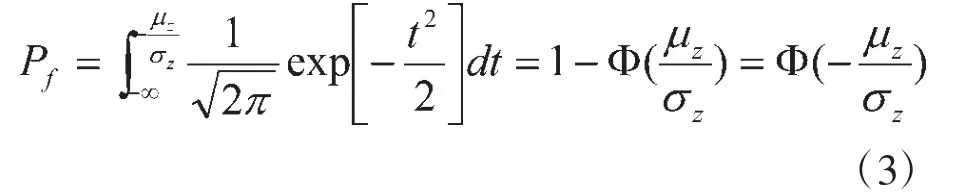
3.2可靠指標與安全系數(shù)的關系

用安全系數(shù)進行工程設計，傳統(tǒng)設計可靠性用安全系數(shù)來表示。安全系數(shù)K定義為：

假設抗力R和荷載S都服從正態(tài)分布，功能函數(shù)Z=R-S。根據(jù)可靠度的概念，可得出安全系數(shù)K與可靠性指標β的關系：

可靠性指標β和安全系數(shù)K的關系與隨機變量R和S的變異系數(shù)有關，β反映了R和S的離散程度。與K相比，β更好地反映了工程安全度的實質。

3.3可靠指標與分項系數(shù)K的關系

分項系數(shù)表達式不采用單一的安全系數(shù)而是對應各變量的分項系數(shù)，各變量的分項系數(shù)是根據(jù)概率可靠度方法確定的。如永久荷載SGk和可變荷載SQk，抗力為Rk，則分項系數(shù)表達式為：

上式中：γR為抗力分項系數(shù)；γG為永久荷載分項系數(shù)；γQ為可變荷載分項系數(shù)。

分項系數(shù)是用分離函數(shù)得到的，其與可靠指標的關系可由計算可靠度的一次二階矩方法導出。

4　可靠指標的計算方法

現(xiàn)階段可靠度計算方法主要有一次二階矩方法、二次二階矩方法、蒙特卡羅模擬法及概率有限法等。其中一次二階矩方法是最常用的方法，本文只對該方法進行簡單介紹。

一次二階矩方法的基本原理是：假定功能函數(shù)Z=g（X1，X2，…，XN）是基本變量Xi=（i=1，2，…，n）的線性函數(shù)，Xi=（i=1，2，…，n）服從正態(tài)分布或對數(shù)正態(tài)分布，且各變量之間相互獨立，則可以由Xi=（i=1，2，…，n）的一階矩、二階矩計算Z的均值μZ和標準差σZ，進而確定可靠性指標β值。對于非線性功能函數(shù)，將Z簡化成Xi=（i=1，2，…，n）的線性函數(shù)，計算出β值。如基本變量為非獨立和非正態(tài)變量，需先對其進行相應的處理，再計算β值。該方法可分為均值一次二階矩方法（中心點法）、改進的一次二階矩方法（驗算點法）和JC法等。

4.1均值一次二階矩方法（中心點法）

均值一次二階矩方法（中心點法）的可靠性指標β確定過程如下。

若功能函數(shù)可以表示為荷載效應S與抗力R的線性關系，荷載效應S與抗力R均服從正態(tài)分布時，可靠性指標β可表示為：

對非線性功能函數(shù)，可先進行線性化處理：

可靠性指標β可表示為：

該方法的優(yōu)點是計算簡便，不必進行過多的數(shù)值計算，但也存在不能考慮隨機變量的分布概型、只能直接取用隨機變量的一階矩和二階矩、極限功能函數(shù)高度非線性情況下會導致誤差過大等缺點。該方法計算結果相對較粗糙，常用于可靠度要求不高的情況。

4.2改進的一次二階矩方法（驗算點法）

在計算過程中為了克服中心點法的缺點，引入了驗算點的概念，驗算點法對中心點法的改進主要在于線性化點選取位置的改變，由中心點法選在均值點，改為選在最大可能失效概率所對應的設計驗算點P*上，從而克服中心點法所產(chǎn)生的問題。β的計算只能采用迭代法。

4.3JC法

在實際工程中，并不是所有變量都是正態(tài)分布的，JC法則很好地解決了這個問題。其基本原理是先把非正態(tài)分布變量進行當量正態(tài)化，然后利用一次二階矩驗算點法求解可靠度指標，一般采用迭代法計算。

JC法原理較簡單，計算收斂快，是比較實用的可靠度分析方法。但也存在一些缺點，如：當基本隨機變量不全服從正態(tài)分布時，采用當量正態(tài)分布代替實際非正態(tài)分布進行計算，會帶來一定誤差；另外，該方法不能考慮基本隨機變量之間的相關性。

5　我國巖土工程可靠度分析的特點及發(fā)展現(xiàn)狀

5.1巖土工程的不確定性問題

我們知道，巖土工程具有其自身的特點，存在大量的不確定性問題和因素，巖土工程中的不確定性主要有（巖）土層分布的不確定性、現(xiàn)場和室內(nèi)試驗所測巖土指標的不確定性、現(xiàn)場應力分布與孔壓分布的不確定性、外加荷載和分布的不確定性以及計算模式的不確定性等。

巖土具有非均一性，其性質復雜多變，其變異性比其它材料要大得多。在巖土工程研究過程中，取樣、試驗、試驗數(shù)量、成果整理分析等各個環(huán)節(jié)都會出現(xiàn)問題，帶來不確定性和測值的變異性。

5.2巖土工程可靠性分析的特點

對巖土工程來說，是對整個工程范圍進行整體驗算，不論是穩(wěn)定問題或變形問題，求解的是整個地基或整個工程的影響范圍的綜合反應，計算模型和涉及的參數(shù)方面都比較復雜。

地基基礎設計中的承載力極限狀態(tài)，既包含了地基整體失穩(wěn)所引起的狹義上的承載力極限狀態(tài)，也包含由于巖土的位移、局部破壞或者變形過大而導致的上部結構的破壞，即變形的極限狀態(tài)也會引起承載力的極限狀態(tài)，兩者不是完全獨立的。

巖土或地基基礎工程中尺寸或所研究的范圍一般均較大。室內(nèi)小尺寸的試件如何代表實際工程的性狀，由于研究的范圍大，決定巖土工程或地基基礎工程性狀的因素為空間平均巖土特性。

（巖）土的本構模型多種多樣，具有高度的非線性，在不同的應力水平下，巖土會表現(xiàn)出不同的變形特性，相應的極限狀態(tài)方程也可能是非線性的。

土性指標的相關性。巖土性質指標具有相關性，既有不同指標間的互相關性，也有同一指標的自相關特性。

巖土工程計算方法具有多樣性和不確定性。有一定程度的主觀隨意性。

此外，巖土工程的系統(tǒng)可靠度問題、全概率問題與廣義可靠度問題，和其他工程結構相比，也具有更復雜的特點。

5.3發(fā)展現(xiàn)狀及存在的問題

我國對巖土工程可靠度的研究始于20世紀50年代末，雖起步較晚，但在某些方面，取得了不少成果。而在某些領域的研究發(fā)展較慢，如巖石方面、土動力學方面展研究較少。

近年來，我國的巖土工程可靠性研究發(fā)展較快，在許多領域取得了豐碩的研究成果。如在上海、天津等地將概率極限狀態(tài)設計方法用于地基基礎設計規(guī)范，并已經(jīng)實施，推動了巖土工程可靠性研究的實用化進程。

目前存在的問題是，土木工程往往是結構工程與巖土工程的組合，結構與巖土相互作用，前者已經(jīng)應用可靠度設計，后都仍沿用傳統(tǒng)的定值方法，處理好兩者關系成了一個難題，國際上采用可靠度設計的巖土工程規(guī)范，據(jù)了解實施情況也并不很理想。我國由于巖土工程固有的特點和積累的不足，普遍推行概率極限設計還存在困難。

巖土工程是一門綜合學科，也是一項系統(tǒng)工程，它包括巖土工程勘察、設計、施工、監(jiān)測和運營各個環(huán)節(jié)，如何將系統(tǒng)可靠度理論、全概率理論和廣義可靠度理論引入和應用到巖土工程，是今后的重要發(fā)展方向，有待我們進一步去完善和思考。

［1］高大釗.土力學可靠性原理［M］.北京：中國建筑工業(yè)出版社，1989.

［2］包承鋼，高大釗.地基工程可靠度分析方法研究［M］.武漢：武漢測繪大學出版社，1997.

［3］高大釗.關于巖土力學新分析方法的問題和思考［J］.工程建設，2006（1）.

［4］高謙，吳順川，等.土木工程可靠性理論及其應用［M］.北京：中國建材工業(yè)出版社，2007.

TU43

B

1007-7359（2016）04-0154-03

10.16330/j.cnki.1007-7359.2016.04.061

張啟兵（1977-），男，安徽蚌埠人，本科，高級工程師，主要從事水利水電工程勘察工作。