基于跨中位移影響線的箱梁損傷定位研究

張珂苑，藺鵬臻

（蘭州交通大學甘肅省道路橋梁與地下工程重點實驗室，甘肅蘭州730070）

基于跨中位移影響線的箱梁損傷定位研究

張珂苑，藺鵬臻

（蘭州交通大學甘肅省道路橋梁與地下工程重點實驗室，甘肅蘭州730070）

為了實現箱梁橋的損傷定位，利用梁式橋結構損傷必然影響彎曲剛度，則梁體跨中撓度影響線將不再以跨中為軸對稱分布這一特點，提出了以橋梁損傷前后跨中撓度影響線三次差值為指標的損傷定位方法。對一座簡支箱梁橋按照單一部位損傷和多部位同時損傷予以分析計算，在預設損傷部位均出現了損傷指標的明顯突變，表明該方法對箱梁的單部位和多部位損傷定位具有較好的適用性。

橋梁；影響線；損傷定位；箱梁；跨中撓度

在我國的橋梁建設中，混凝土開裂是箱梁橋最普遍的病害形式之一，嚴重影響了結構的承載力和長期使用性能。最典型的裂縫是邊跨現澆段和支座附近至1/4跨范圍內的腹板斜裂縫［1-3］。在復雜的服役環境中，橋梁結構受到設計載荷的作用、材料的老化及各種突發性外在因素的影響而面臨結構損傷累積、威脅到橋梁結構安全的問題。因此，研究了識別和檢測結構損傷的理論和方法，建立了結構損傷識別系統，對結構進行在線監測和損傷識別研究，對結構的安全性、可靠性及結構的剩余壽命進行科學、準確地評估。

結構損傷識別是通過對結構的關鍵性能指標的測試和分析，判斷結構是否受到損傷；如果結構受到損傷，檢測損傷位置和損傷大小。根據使用的測量數據類型，現有的損傷識別技術可以分為2大類：①基于靜態測量數據的結構損傷識別方法，以靜態測量數據（如靜態位移、靜態應變等）對損傷進行識別［4］；②基于動態測量數據的結構損傷識別方法，運用動態測量數據（如固有頻率、模態振型、柔度等）對損傷進行識別。由于橋梁在施工時難免會有幾何尺寸方面的誤差，且材料（如混凝土）本身的彈性模量具有一定的不確定性，將直接導致未損傷的主梁的局部抗彎剛度并非為均勻的抗彎剛度。為此，陳記豪等［5］針對簡支空心板橋建立了基于對稱撓度差值影響線的損傷識別方法；劉綱、杜永峰等［5-6］對簡支梁提出了利用某一點在損傷前后的位移（撓度）影響線變化來識別損傷的方法。但這些方法均沒有專門考慮主梁抗彎剛度的不確定性，王藝霖等［8］基于跨中位移影響線差值指標，建立了考慮抗彎剛度不確定性的簡支梁橋損傷定位方法。本文基于跨中位移影響線差值指標，研究簡支箱梁的新型損傷定位方法。

1　損傷指標的建立

1.1移動荷載作用下跨中撓度的計算

主梁分析模型見圖1。其中，l為跨度，EI為主梁完好狀態的截面抗彎剛度。讓一個集中荷載P在主梁上移動，用結構力學中的力法計算跨中位移［9］。

圖1　主梁分析模型

當移動荷載P作用在xP位置時，根據式（1）計算梁端x位置截面的彎矩MP（x）。由力法原理可知，為求跨中撓度，需要通過式（2）計算單位力作用在跨中時距梁端x位置截面的彎矩

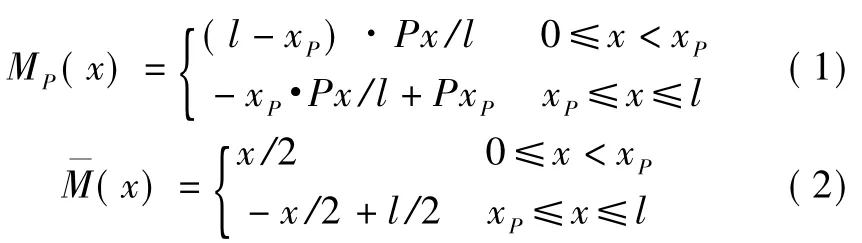
則跨中撓度為

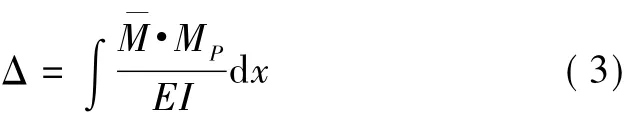
1.2損傷定位指標的建立

假設由于某些因素導致梁體在距離左端x'處有一損傷，損傷使得該部位梁體抗彎剛度改變為αEI，其中α為損傷前后的抗彎剛度改變系數。將主梁沿縱向劃分為長度均等于m的若干區間，則可用m表示損傷區域長度。將荷載作用在xP處時跨中位移的增量記為ΔxP，荷載作用在l-xP處時跨中位移的增量記為Δl-xP，二者的差值記為βxP。分別計算當荷載作用位置xP為x'-3m，x'-2m，x'-m，x'，x'+m，x'+2m，x'+3m，x'+4m時的βxP，見式（4）～式（11）。

由式（4）～（11），可得到

令γxP=βxP-βxP-m表示跨中位移影響線二次差值，則

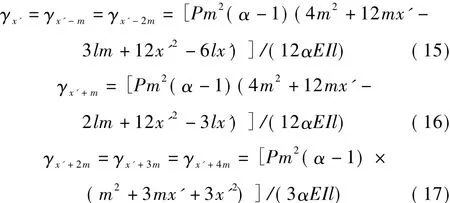
式（18）中，γW與γS分別表示梁體發生損傷前、后跨中位移影響線的二次差值，而Δγ為其三次差值。

對于未發生損傷的理想箱梁（α=1），由式（15）～（17）可以明顯看出，γWxP≡0，所以Δγ=-γSxP；當主梁出現如圖1所示的損傷后，γSxP發生突變，即Δγ發生突變，據此可以進行損傷定位。測量移動荷載作用下跨中的撓度時，需計算沿橋縱向不同位置的Δγx，如果距梁左端x處的Δγx發生突變，則損傷出現在區間［x-m，x］或其對稱區間［l-x，l-x+m］。

2　箱梁中的損傷定位

一跨度為24 m的預應力混凝土簡支箱梁橋［10］，其截面尺寸如圖2所示，理想彈性模量為34.5 GPa，箱梁承受的最不利荷載按照荷載組合原理等效為500 kN的集中力。

圖2　截面尺寸（單位：mm）

假設橋梁在運營中，分別在箱梁頂板、底板和翼緣板出現了損傷，應用前述方法進行損傷定位。為了便于分析，箱梁不同部位的損傷采用沿截面橫向寬度10 mm、深度50 mm的缺損來模擬。此外，考慮施工中由于截面誤差、材料性能等造成梁體為非均勻剛度梁，假設本例分析中初始抗彎剛度在（0.98～1.02）EI隨機分布。

2.1單一部位損傷

設梁體在使用中在［6.0 m，7.5 m］出現損傷，將主梁進行等長區間劃分，每個區間長度為0.5 m，并結合桿系有限元法計算梁體位移，利用式（18）計算主梁損傷前后的Δγ。單一部位損傷Δγ分布曲線見圖3，單一部位損傷的梁體損傷定位指標γ和Δγ見表1。

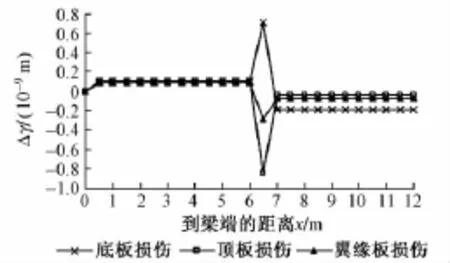
圖3　單一部位損傷Δγ分布曲線

由表1和圖3可以看出，當模擬頂板在［6.0 m，7.5 m］出現損傷時，Δγ在x=6.5 m處發生明顯突變；對于底板和懸臂板模擬的損傷情況，Δγ在x=6.5 m處均出現明顯突變，與事先設定的損傷位置完全對應，表明本文提出的損傷定位方法可完全識別出箱梁出現損傷的單個部位。

表1　單一部位損傷的梁體損傷定位指標γ和Δγm

2.2多個部位損傷

假設橋梁腹板出現4條不同裂縫：

①在x=1.1 m出現長0.3 m的縱向裂縫，記為A；

②在x=8.99 m出現長0.6 m的豎向裂縫，記為B；

③在x=17.3 m出現長1.2 m的縱向裂縫，記為C；

④在x=20.2 m出現長0.8 m的縱向裂縫，記為D。

基于本文理論計算得到多部位損傷的梁體損傷定位指標γ和Δγ見表2，多部位損傷指標Δγ分布曲線見圖4。

表2　多部位損傷的梁體損傷定位指標γ和Δγm

圖4　多部位損傷指標Δγ分布曲線

由表2和圖4可以看出，當模擬腹板的損傷出現在［1.0 m，1.5 m］時，Δγ在x=1.5 m處發生明顯突變，對應事先設定的損傷位置A；Δγ在x=3.5 m，x= 4.0 m處發生明顯突變，對應事先設定的損傷位置D；Δγ在x=6.0 m，x=6.5 m，x=7.0 m處發生突變，對應事先設定的損傷位置C；Δγ在x=9.0 m處發生突變，對應事先設定的損傷位置B。表明本文提出的損傷定位方法可以完全識別出箱梁出現損傷的多個部位。

3　結語

本文基于當簡支梁某一段出現損傷后，梁體跨中撓度影響線將不再以跨中為軸對稱分布這一特點，提出了以橋梁損傷前后跨中撓度影響線三次差值Δγ為指標的損傷定位方法。對于算例中，簡支箱梁頂板、底板、懸臂板和腹板出現的不同損傷，通過計算損傷指標，發現在預設損傷部位均出現了損傷指標的明顯突變。表明本方法對簡支箱梁不同部位不同損傷的定位是準確的。

［1］丁勇，趙啟林，馬方圓，等.普通鋼筋混凝土箱梁橋腹板豎向裂縫成因分析［J］.工業建筑，2009，36（增1）：919-922.

［2］巴力，王凱.大空心板梁跨中斜向裂縫的成因分析［J］.鐵道建筑，2015（11）：18-20.

［3］職雨風，金濱.25 m小箱梁縱向裂縫分析及處治實例［J］.廣東公路交通，2002，76（增）：194-195.

［4］TOMASZEWSKA A.Influence of Statistical Errors on Damage Detection Based on Structural Flexibility and Mode Shape Curvature［J］.Computer and Structures，2010，88（3/4）：154-164.

［5］陳記豪，趙順波，姚繼濤.基于對稱撓度差值影響線的裝配式簡支空心板橋上部結構損傷識別［J］.應用基礎與工程科學學報，2014，22（2）：283-293.

［6］劉綱，黃宗明，高建莉.基于損傷力影響線的靜定梁損傷識別研究［J］.湖南大學學報（自然科學版），2009，36（8）：23-27.

［7］杜永峰，劉云帥，王曉琴.基于撓度差值影響線曲率的簡支梁橋損傷識別［J］.橋梁建設，2009（4）：80-83.

［8］王藝霖，張鑫，安新梅.考慮抗彎剛度不確定性的簡支梁橋損傷定位方法［J］.中國公路學報，2015，28（3）：82-87.

［9］李廉錕.結構力學［M］.北京：高等教育出版社，2010.

［10］葛繼平，王志強，彭大文，等.重復荷載下高鐵24 m箱梁模型試驗研究［J］.武漢理工大學學報（交通工程與科學版），2013，37（4）：741-744.

（責任審編鄭冰）

Study on Box Girder Damage Location Based on Mid-span Displacement Influence Line

ZHANG Keyuan，LIN Pengzhen
（Key Laboratory of Road&Bridge and Underground Engineering Gansu Province，Lanzhou Jiaotong University，Lanzhou Gansu 730070，China）

In order to realize the damage location of the box girder bridge，a damage location method is proposed by using the characteristics of the girder bridges damage will inevitably affect the bending rigidity and the influence line of the mid-span deflection of the beam will no longer be symmetrical，which is the third difference of the influence line of the mid-span deflection before and after the bridge damage.A simple supported box girder bridge with single site and multiple sites damage condition were analyzed and calculated，then the damage index of the preset position was found to have a significant mutation.T he results show that the method is applicable for single site and multiple sites damage condition location of the box girder.

Bridge；Influence line；Damage location；Box girder；M id-span deflection

U441+.4

A

10.3969/j.issn.1003-1995.2016.10.02

1003-1995（2016）10-0006-04

2016-04-07；

2016-08-10

國家自然科學基金（51168030，51208242，51368031）；甘肅省基礎研究創新群體項目（1506RJIA029）

張珂苑（1991—），男，碩士研究生。

藺鵬臻（1977—），男，教授，博士。