附加質量模型在拱壩自振特性分析中的應用

趙麗華　陳麗剛　楊振琨

(黃河勘測規劃設計有限公司，河南 鄭州　450003)

?

·水利工程·

附加質量模型在拱壩自振特性分析中的應用

趙麗華陳麗剛楊振琨

(黃河勘測規劃設計有限公司，河南 鄭州450003)

基于附加質量模型的缺陷，提出了附加質量折半模型，采用該模型分析了拱壩的自振特性，并與原計算模型試驗結果作了對比分析，結果表明：相對于附加質量模型，附加質量折半模型計算所得的壩體自振頻率更符合實際，但偏差仍相對較大。

附加質量模型，自振特性，拱壩，模態分析

拱壩的自振特性可以通過現場原型激振試驗獲取，為以后的數值模擬校正材料參數，盡量減少計算中的不確定因素，對工程的安全評價具有重要的工程意義。拱壩的自振頻率與水位密切相關[1]，庫水對壩體的作用常采用簡單而實用的附加質量模型處理。以往的研究表明，附加質量模型求得的附加質量偏大，導致壩體自振頻率偏低[2,3]。本文通過將附加質量折半進行壩體自振特性分析，希望獲得更符合實際的壩體自振頻率。

1　附加質量模型

附加質量法是一種考慮庫水對壩體作用的簡化計算模型，它將庫水的動水壓力等效成質量附加在壩體上以考慮壩體的動力響應。附加質量法并沒有考慮壩體—庫水動力相互作用的影響。

1933年，Westergaard在研究庫水的動水壓力問題時，選取垂直剛性壩面，施加水平簡諧地面運動的外荷載，將庫水的動水壓力近似為沿水深方向呈拋物線形式分布，同時根據實測的動水壓力作用在壩踵的彎矩與模擬的動水壓力分布作用在壩踵的彎矩相等的條件，得出水深h處壩面的動水壓力的近似公式[4]：

(1)

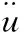
與慣性力的原理相似，用附著于結構面上的一定質量水體的慣性力代替庫水的動水壓力作用，由此得到Westergaard附加質量公式：

(2)

其中，Mp(h)為水深h處的庫水附加質量；ρ為庫水密度；h為計算點庫水的水深。

Westergaard附加質量公式計算簡單方便，但其適用于垂直剛性面的假設條件。1982年，Clough教授對Westergaard附加質量公式進行了修正，其能適用于任意形狀的壩面，并可以考慮任意方向的地震加速度：

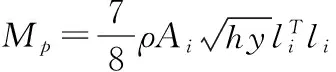
其中，li為結構面上某點i的法線矢量；Ai為該點在結構面上的控制面積。

2　拱壩自振特性分析的數值模擬

拱壩本身具有無限自由度，而自振特性的求解需要有限的自由度。有限元理論就是將具有無限自由度的空間結構體系離散成一個具有有限自由度的空間結構系統的一種近似數值算法。這樣壩體就具有了有限個固有頻率和振幅[5]。

不考慮阻尼和外力，n個自由度系統振動微分方程為：

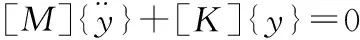
(3)

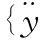
當研究庫水附加質量模型對拱壩自振特性的影響時，可以忽略阻尼作用，其壩體的自由振動方程最后簡化為：

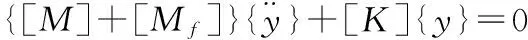
其中，[M]，[Mf]，[K]分別為結構的質量矩陣，附加質量矩陣和剛度矩陣。

根據微分方程組和模態分析理論，可得第k階頻率公式：

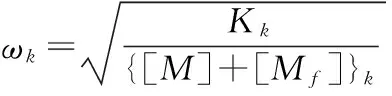
3　算例分析

3.1工程概況

某拱壩為三心圓單曲碾壓混凝土拱壩，拱壩中心線與河流流向基本平行。為合理利用地形條件，改善拱壩壩體應力，在河床底部設置墊座，墊座高15 m，寬44 m。壩頂高程1 867.5 m，最低基建面高程1 735.50 m，最大壩高132.0 m，最大中心角48.90°，最小中心角16.45°，頂拱中心線弧長250.25 m，弧高比為1.90，拱冠梁頂部厚9.5 m，底部厚28 m，厚高比約0.238。

3.2計算模型

模態分析假定結構都是線性的，分析中假定混凝土、基礎巖石體均為各向同性線彈性材料。計算中壩體混凝土的彈性模量取為2.51×104MPa，泊松比為0.167，密度為2 400 kg/m3。本文采用無質量地基模型模擬壩基，壩基范圍取1.5倍壩高，向上下游和兩側取1.5倍壩高。基巖材料的彈性模量取為1.75×104MPa，泊松比取為0.23。庫水密度取為1 000 kg/m3，未考慮水體壓縮性。整個壩體離散為3 540個8節點三維等參單元，壩基離散為20 635個8節點三維等參單元，假定地基單元以外的基巖為剛性，基礎全部邊界節點施加法向約束。坐標原點高程1 750.0 m，位于拱壩中段圓心處。Y坐標軸為順河流向，向上游為正方向，X坐標軸為橫河向，左岸為正方向，Z坐標軸為豎直向，向上為正方向。壩體、壩基離散網格模型見圖1。

3.3自振特性分析

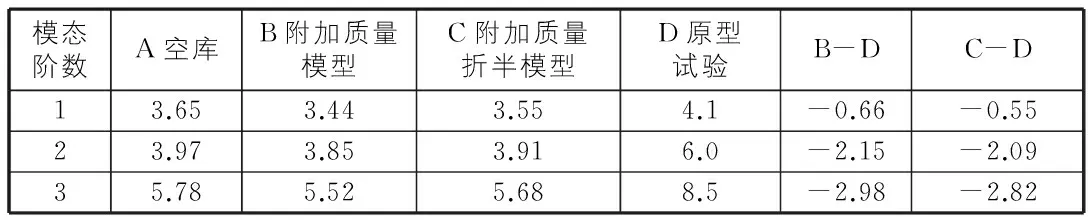
為了與原型實驗[6]結果比較，選取試驗工況時的蓄水位計算。由于受試驗精度等因素的影響，識別工作有時比較困難，本次僅選取前3階自振頻率進行對比。表1列舉了空庫、附加質量模型、附加質量折半模型和原型試驗的壩體前3階自振頻率。

表1　壩體各模型下的自振頻率比較表(試驗水位)

模態階數A空庫B附加質量模型C附加質量折半模型D原型試驗B-DC-D13.653.443.554.1-0.66-0.5523.973.853.916.0-2.15-2.0935.785.525.688.5-2.98-2.82

通過分析可得：相對于空庫情況，附加質量模型降低了壩體的自振頻率，這主要是由于壩體受庫水動水壓力的影響。與原型試驗結果相比，附加質量模型和附加質量折半模型壩體的1階自振頻率分別降低了16.1%，13.4%。相比附加質量模型，附加質量折半模型降低值相對較小，更接近原型試驗結果。隨著模態階數的增加，附加質量模型和附加質量折半模型與原型試驗的差值進一步擴大。由于試驗是在略高于大壩運行低水位(死水位)的情況時進行的，庫水附加質量模型對壩體自振頻率的影響相對較小。為進一步分析附加質量模型對壩體自振頻率的影響，選取正常蓄水位工況進行計算，結果見表2。

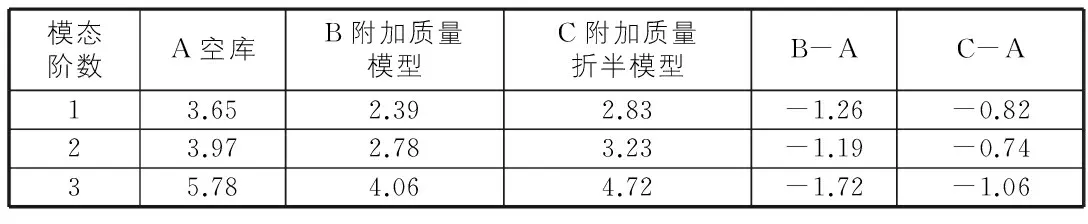
表2　壩體各模型下的自振頻率比較表(正常蓄水位)

通過對比表1，表2分析可得：相對于試驗時水位，正常蓄水位對壩體自振頻率的影響更大。與空庫計算結果相比，附加質量模型和附加質量折半模型壩體的1階自振頻率分別降低了34.5%，22.5%。可以看出，隨著水庫水位的增加，附加質量折半模型對拱壩自振頻率的修正相對附加質量模型效果更好。

4　結語

本文提出了對庫水附加質量模型進行修正的折半計算方法，與原計算模型相比，計算結果與實測結果更接近。這與文獻[2]的試驗結論是一致的。但結果偏差仍相對較大，如何選取更合理的修正模型需要進一步研究。

[1]寇立夯.基于性能的高壩抗震設計若干關鍵問題研究[D].北京:清華大學博士學位論文，2009.

[2]陳厚群，侯順載，楊大偉.地震條件下拱壩庫水相互作用的試驗研究[J].水利學報，1989(7):29-39.

[3]杜成偉，柴軍瑞，白峰，等.附加質量模型和壩庫系統流固藕合模型的比較分析——現代水利水電工程抗震防災研究與進展[M].北京:中國水利水電出版社，2009:338-343.

[4]Westergaard.Water pressures on dams during earthquakes[J].Trans.ASCE，1933(98):418-472.

[5]馮濤，李慶亮，孫大為.基于ANSYS的拱壩模態分析[J].河南科學，2011,29(9)：1081-1084.

[6]胡曉.沙牌拱壩抗震性能計算分析報告沙牌拱壩現場試驗研究報告[R].北京：中國水利水電科學研究院，2009.

Application of added mass model in the analysis of arch dam natural vibration characteristics

Zhao LihuaChen LigangYang Zhenkun

(YellowRiverEngineeringConsultingCo.,Ltd.(YREC),Zhengzhou450003,China)

Based on defects of additional quality model, the paper puts forward additional quality binary model, analyzes the arch dam self-vibration properties by applying the additional quality binary model, and makes a comparison with original calculation model. Results show that: comparing to additional quality model, the dam self-vibration frequency calculated with additional quality binary model better meets practice. However, it has larger deviation.

additional quality model, self-vibration property, arch dam, modal analysis

1009-6825(2016)19-0207-03

2016-04-28

趙麗華(1987- )，女，工程師；陳麗剛(1984- )，男，工程師；楊振琨(1986- )，男，碩士，工程師

TV311

A