不確定高階MIMO系統(tǒng)的指對(duì)數(shù)型終端滑模控制

傅佳燁， 牛玉剛（華東理工大學(xué)化工過(guò)程先進(jìn)控制和優(yōu)化技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室，上海 200237）

不確定高階MIMO系統(tǒng)的指對(duì)數(shù)型終端滑模控制

傅佳燁， 牛玉剛
（華東理工大學(xué)化工過(guò)程先進(jìn)控制和優(yōu)化技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室，上海 200237）

針對(duì)一類(lèi)不確定高階MIMO線(xiàn)性系統(tǒng)，提出了一種新型指對(duì)數(shù)型終端滑模控制方法。所設(shè)計(jì)的非線(xiàn)性指對(duì)數(shù)型終端滑模面，不僅能保證滑模動(dòng)態(tài)的有限時(shí)間穩(wěn)定，而且具有更快的收斂速度。同時(shí)，滑模控制器能夠保證滑模面的有限時(shí)間可達(dá)性。最后，通過(guò)數(shù)值仿真驗(yàn)證了本文方法的有效性。

終端滑模控制；MIMO系統(tǒng)；指對(duì)數(shù)型

在實(shí)際工業(yè)生產(chǎn)過(guò)程中，控制系統(tǒng)常常受到各種不確定性的影響，包括系統(tǒng)參數(shù)攝動(dòng)以及外界干擾等，這些不確定性不僅會(huì)影響系統(tǒng)性能，嚴(yán)重時(shí)甚至?xí)?dǎo)致系統(tǒng)失穩(wěn)，因而對(duì)于不確定系統(tǒng)的研究一直都是控制領(lǐng)域的研究熱點(diǎn)。滑模變結(jié)構(gòu)控制由于其對(duì)系統(tǒng)參數(shù)攝動(dòng)以及外界干擾具有良好的魯棒性［1］，成為處理不確定系統(tǒng)控制問(wèn)題的一種有效的魯棒控制方法。

傳統(tǒng)的線(xiàn)性滑模面雖然能保證系統(tǒng)狀態(tài)沿滑模面漸近穩(wěn)定（即當(dāng)時(shí)間趨于無(wú)窮大時(shí)，狀態(tài)漸近收斂于狀態(tài)原點(diǎn)），卻不能實(shí)現(xiàn)有限時(shí)間收斂。然而在許多實(shí)際應(yīng)用中（例如剛性機(jī)器人的控制、航天航空中的飛行器控制等），常常要求系統(tǒng)狀態(tài)能夠在有限時(shí)間內(nèi)收斂到平衡點(diǎn)。終端滑模控制（Terminal Sliding Mode Control，TSMC）方法正是針對(duì)這個(gè)問(wèn)題提出的［2-3］，其主要思想是采用非線(xiàn)性滑模面，使得系統(tǒng)狀態(tài)到達(dá)滑模面后能夠在有限時(shí)間內(nèi)收斂到平衡點(diǎn)。針對(duì)二階系統(tǒng)，文獻(xiàn)［4-7］分別提出了快速、指數(shù)型、對(duì)數(shù)型、指對(duì)數(shù)型等終端滑模面，提高了系統(tǒng)狀態(tài)在滑模面上的收斂速度。文獻(xiàn)［8-9］提出非奇異終端滑模面，解決了終端滑模控制的奇異性問(wèn)題。文獻(xiàn)［10］提出了非奇異快速終端滑模面。然而，針對(duì)高階MIMO線(xiàn)性系統(tǒng)，終端滑模控制的研究成果相對(duì)比較少［11-14］，主要是因?yàn)榻K端滑模最初是針對(duì)二階系統(tǒng)提出的，不像傳統(tǒng)的線(xiàn)性滑模控制方法，很難直接推廣到高階多輸入系統(tǒng)。這也是目前終端滑模控制在高階多輸入系統(tǒng)研究中的一個(gè)難點(diǎn)。

本文針對(duì)一類(lèi)不確定高階MIMO線(xiàn)性系統(tǒng)，提出了一種新型指對(duì)數(shù)型終端滑模面，同時(shí)設(shè)計(jì)相應(yīng)的滑模控制器，使得系統(tǒng)狀態(tài)能夠在有限時(shí)間內(nèi)收斂到平衡點(diǎn)，且收斂速度快于已有的高階終端滑模控制。

1　系統(tǒng)描述

其中：X（t）∈Rn為系統(tǒng)狀態(tài)變量；U（t）∈Rm為系統(tǒng)控制輸入；A∈Rn×n和B∈Rm×n是已知的系統(tǒng)參數(shù)矩陣；ΔA（t）和F（t）分別代表未知的系統(tǒng)參數(shù)攝動(dòng)矩陣和外界干擾。假定系統(tǒng)滿(mǎn)足以下假設(shè)：

（1）標(biāo)稱(chēng)系統(tǒng)（A，B）可控，且B列滿(mǎn)秩；（2）ΔA（t）、F（t）滿(mǎn)足以下匹配條件：

不同于文獻(xiàn)［11］，本文考慮的系統(tǒng)模型滿(mǎn)足式（2）～式（3）所示的匹配條件，是為了在后面的設(shè)計(jì)過(guò)程中使得系統(tǒng)狀態(tài)在有限時(shí)間內(nèi)收斂到平衡點(diǎn)，而不是平衡點(diǎn)附加的一個(gè)鄰域內(nèi)。

考慮如下不確定高階MIMO線(xiàn)性系統(tǒng)

2　指對(duì)數(shù)型終端滑模面的設(shè)計(jì)

2.1系統(tǒng)模型轉(zhuǎn)換

由B列滿(mǎn)秩可知，存在可逆矩陣T使得TB= ［0 B2］T成立，其中B2∈Rm×m是滿(mǎn)秩矩陣，且有

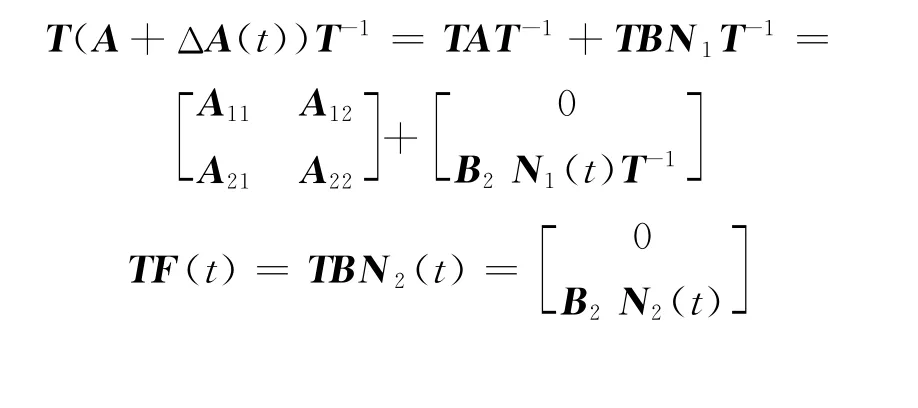
由于Z（t）與X（t）呈線(xiàn)性關(guān)系，當(dāng)Z（t）→0時(shí)，X（t）→0。這樣所研究的問(wèn)題等價(jià)于對(duì)系統(tǒng)（4）進(jìn)行終端滑模設(shè)計(jì)，使系統(tǒng)狀態(tài)在有限時(shí)間內(nèi)收斂到零。

2.2指對(duì)數(shù)型終端滑模面設(shè)計(jì)及穩(wěn)定性分析

文獻(xiàn)［7］提出了如下的指對(duì)數(shù)型終端滑模面：

式中：x∈R；a＞0；β＞0；p，q滿(mǎn)足q＜p＜2q且為正奇數(shù)。從式（5）可以看出，一般指對(duì)數(shù)型終端滑模面適用于SISO系統(tǒng)，而不能直接應(yīng)用到MIMO系統(tǒng)。

本文將式（5）所示的指對(duì)數(shù)型終端滑模面拓展到式（4）所示的MIMO系統(tǒng)中，設(shè)計(jì)指對(duì)數(shù)型終端滑模面為

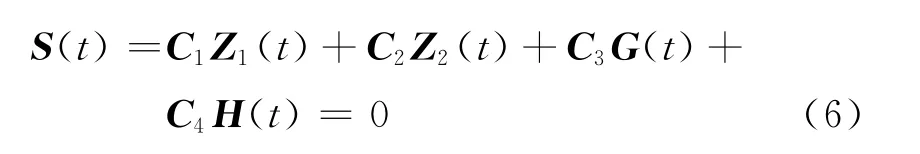
式中，G（t）和H（t）分別定義如下：

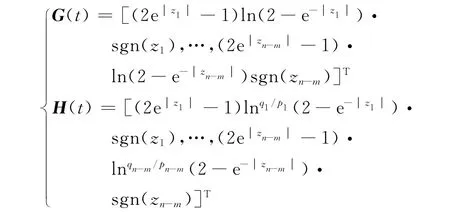
其中：pi，qi滿(mǎn)足qi＜pi＜2qi，（i=1，…，n－m）且為正奇數(shù)。

另外，式（6）中C1∈Rm×（n－m），C2∈Rm×m，C3∈Rm×（n－m），C4∈Rm×（n－m）為終端滑模面的參數(shù)矩陣，其中C2是一個(gè)滿(mǎn)秩矩陣，即rank（C2）=m。設(shè)計(jì)C1、C2、C3、C4滿(mǎn)足以下條件：

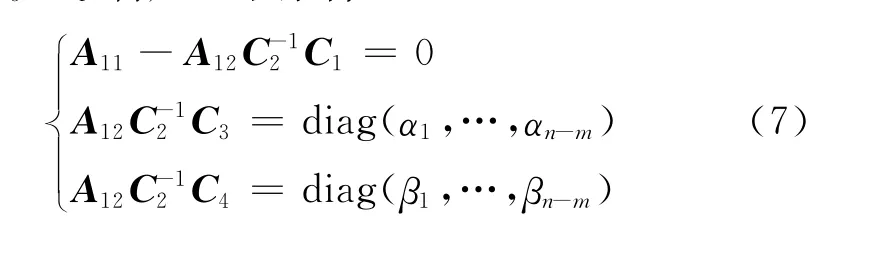
其中，ai＞0，βi＞0，（i=1，…，n－m）。

按照滑模控制理論，當(dāng)系統(tǒng)（4）沿指對(duì)數(shù)型終端滑模面式（5）運(yùn)動(dòng)時(shí)，系統(tǒng)的狀態(tài)方程降為n－m階。由式（5）可以得到

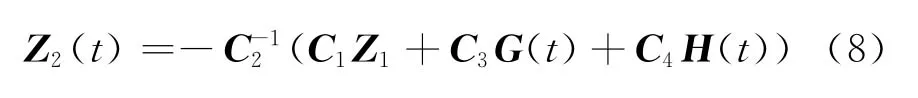
將式（8）代入式（4），可以得到n－m階滑模動(dòng)態(tài)方程為

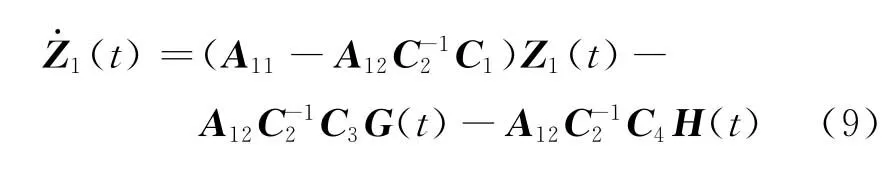
下面分析不確定高階MIMO系統(tǒng)沿指對(duì)數(shù)型終端滑模面（式（6））運(yùn)動(dòng)時(shí)，系統(tǒng)動(dòng)態(tài)在有限時(shí)間內(nèi)收斂到平衡點(diǎn)，同時(shí)系統(tǒng)（8）也在有限時(shí)間內(nèi)收斂到平衡點(diǎn)。

定理1 對(duì)于不確定高階MIMO線(xiàn)性系統(tǒng)（4），設(shè)計(jì)指對(duì)數(shù)型終端滑模面（式（6）），且滑模面參數(shù)矩陣滿(mǎn)足條件式（7），則系統(tǒng)狀態(tài)Z1（t）在到達(dá)滑模面后將在有限時(shí)間內(nèi)收斂到平衡點(diǎn)，同時(shí)Z2（t）也將在有限時(shí)間內(nèi)收斂到平衡點(diǎn)。

證明

（1）穩(wěn)定性。當(dāng)系統(tǒng)狀態(tài)變量進(jìn)入滑模面后，可以得到式（9）所示的滑動(dòng)模態(tài)方程，將滑模面參數(shù)矩陣條件式（7）代入式（9），有

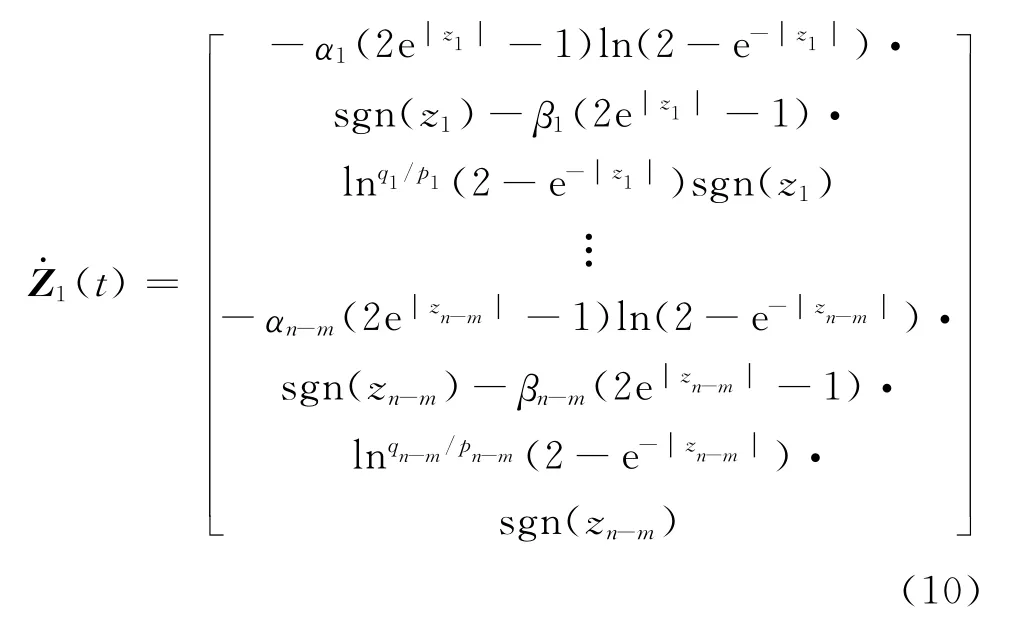
即Z1（t）每個(gè)標(biāo)量zi均滿(mǎn)足：

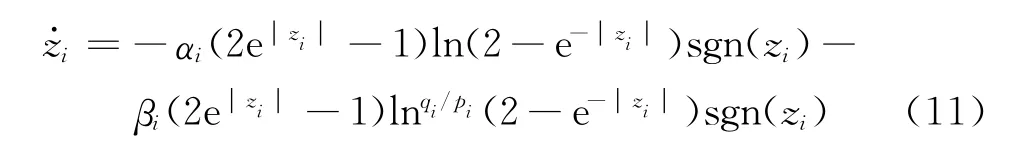
由式（11）可知，zi滿(mǎn)足一般指對(duì)數(shù)型終端滑模面的形式。

選取Lyapunov函數(shù)V1：

對(duì)式（12）求導(dǎo)，可得

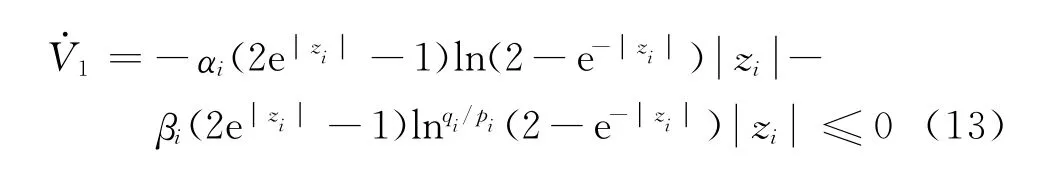
由Lyapunov穩(wěn)定性定理可知，系統(tǒng)是穩(wěn)定的。

（2）有限時(shí)間可達(dá)。當(dāng)系統(tǒng)狀態(tài)到達(dá)滑模面時(shí)，由以上分析過(guò)程可知，式（11）可以表示為

由式（14）、式（15）可得

由一階線(xiàn)性微分方程通解求解理論，式（16）的解為

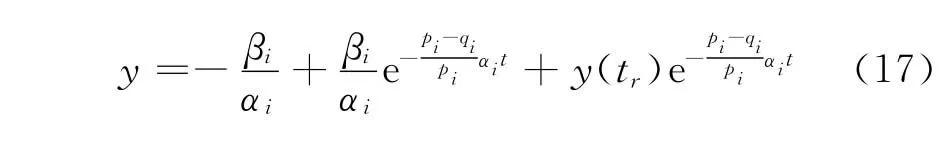
其中，tr為系統(tǒng)從任意初始狀態(tài)到達(dá)滑模面的時(shí)刻。

我們知道，當(dāng)系統(tǒng)狀態(tài)到達(dá)平衡點(diǎn)時(shí)f（zi，tsi）= 0，即y（tsi）=0。根據(jù)式（17），可求得zi將在有限時(shí)間tsi內(nèi)沿滑模面到達(dá)平衡點(diǎn)：

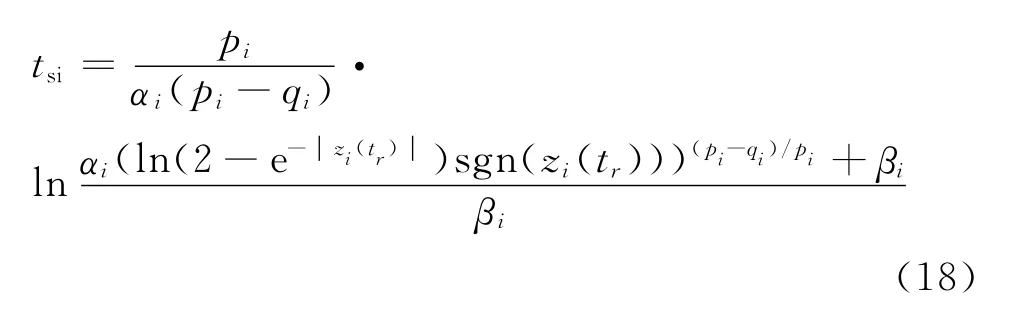
由此證明Z1（t）是有限時(shí)間穩(wěn)定的，并且根據(jù)式（8）可知Z2（t）也是有限時(shí)間穩(wěn)定的，即系統(tǒng)狀態(tài)在到達(dá)滑模面后將在有限時(shí)間內(nèi)收斂到平衡點(diǎn)，且有限時(shí)間滿(mǎn)足證畢。

3　終端滑模控制器的設(shè)計(jì)

對(duì)式（19）求導(dǎo)，可得

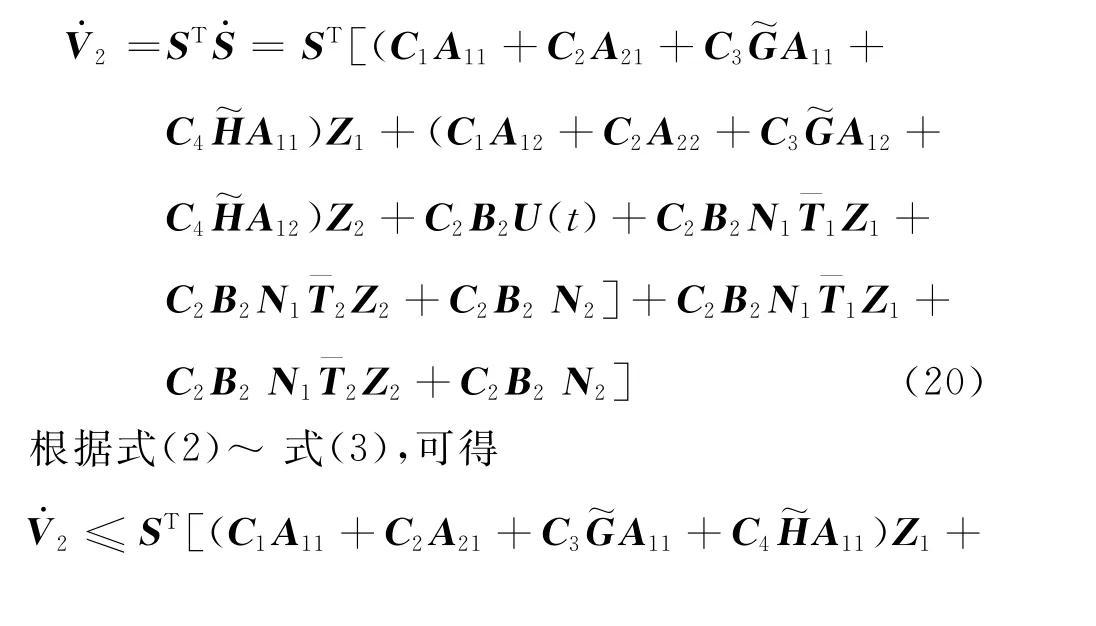
定理1給出了系統(tǒng)狀態(tài)沿終端滑模面有限時(shí)間穩(wěn)定的充分條件。進(jìn)一步設(shè)計(jì)終端滑模控制器保證系統(tǒng)狀態(tài)軌跡能在有限時(shí)間內(nèi)到達(dá)滑模面S（t）=0。

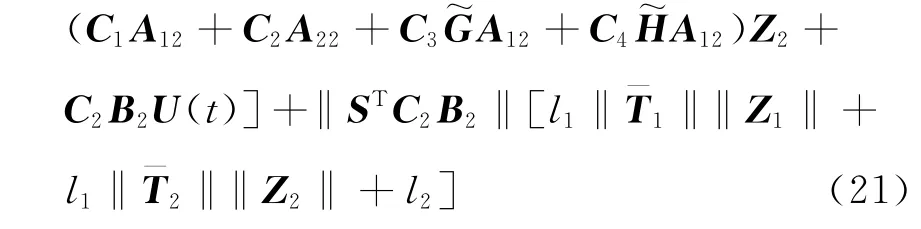
為使滑動(dòng)模態(tài)的可達(dá)性條件成立，設(shè)計(jì)終端滑模控制器如下：

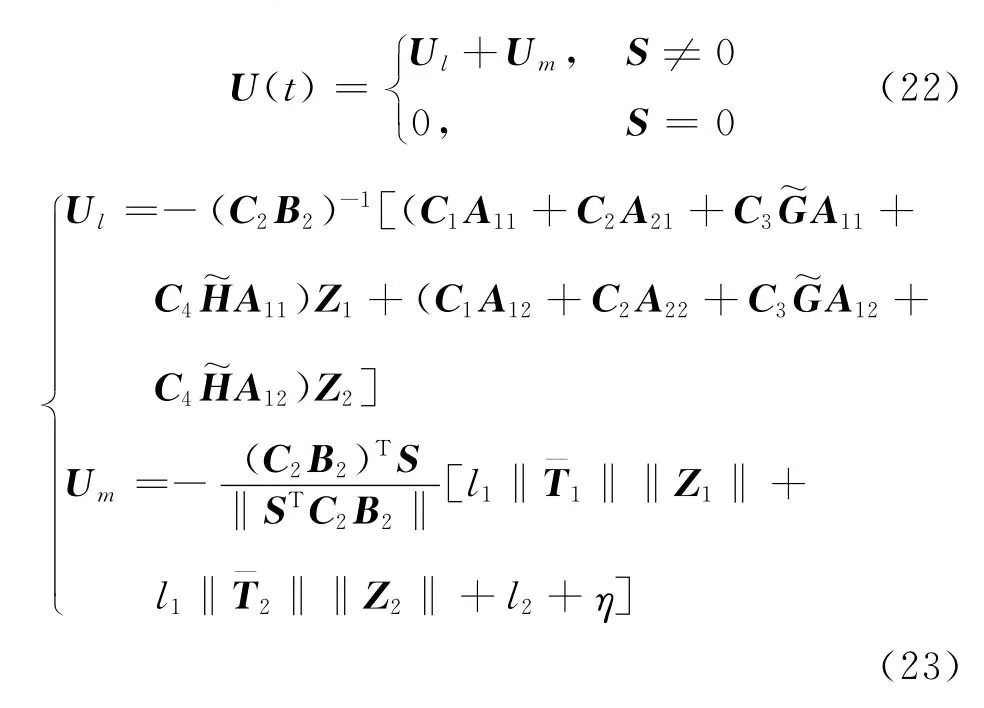
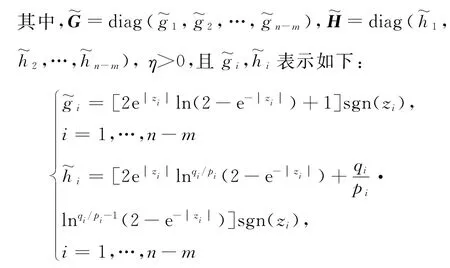
將所設(shè)計(jì)的終端滑模控制器式（22）、式（23）代入式（21），可以得到

由Lyapunov穩(wěn)定性定理可知，系統(tǒng)（4）在有限時(shí)間內(nèi)到達(dá)滑模面，收劍時(shí)間滿(mǎn)足

由以上分析過(guò)程可以得到定理2。

定理2 對(duì)于不確定高階MIMO系統(tǒng)（4）和指對(duì)數(shù)型終端滑模面（式（5）～式（7）），終端滑模控制器為式（22）、式（23）可以保證系統(tǒng)（4）在有限時(shí)間內(nèi)到達(dá)滑模面S=0。

由定理1和定理2可知，對(duì)于任意初始狀態(tài)，系統(tǒng)狀態(tài)Z（t）將在有限時(shí)間t=ts＋tr內(nèi)到達(dá)平衡點(diǎn)，因此，系統(tǒng)狀態(tài)X（t）將在有限時(shí)間內(nèi)到達(dá)平衡點(diǎn)。

4　仿真研究

考慮不確定高階MIMO系統(tǒng)（1），其參數(shù)分別為

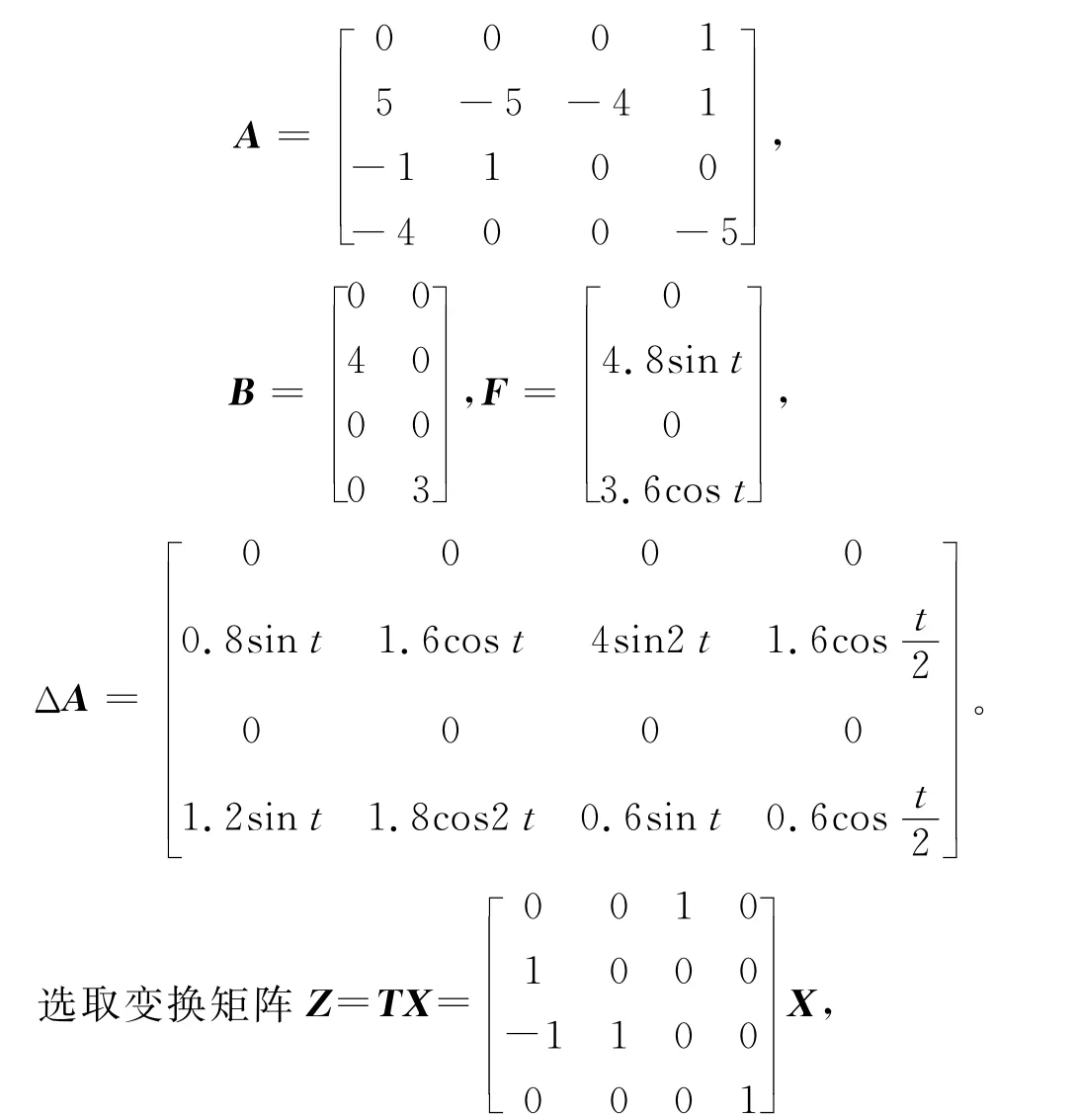
則變換后系統(tǒng)（4）的參數(shù)分別為

根據(jù)滑模面參數(shù)矩陣滿(mǎn)足條件式（7），選取指對(duì)數(shù)型終端滑模面各參數(shù)如下：

按照所設(shè)計(jì)的滑模控制器（式（19）～式（20）），選取控制器各參數(shù)：

為驗(yàn)證本文設(shè)計(jì)的指對(duì)數(shù)型終端滑模控制（ELTSMC）的有效性，分別與已有的快速終端滑模控制（FTSMC）和指數(shù)型終端滑模控制（ETSMC）進(jìn)行仿真比較。其中，快速終端滑模控制為

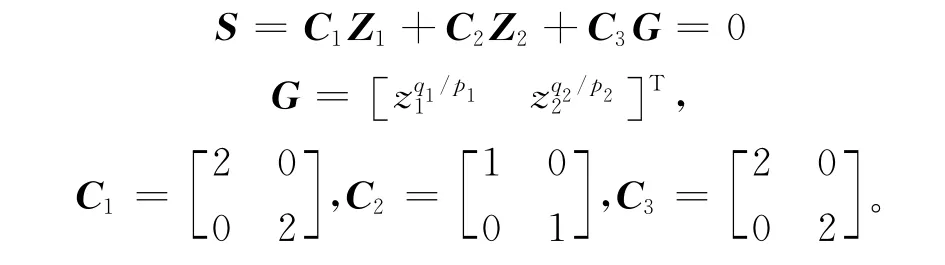
指數(shù)型終端滑模控制為

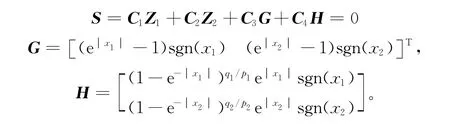
其余參數(shù)相同，仿真步長(zhǎng)設(shè)為0.1 s，系統(tǒng)初始狀態(tài)X（0）=［－0.4－0.6 0.5 0.1］T。

圖1～圖3和圖4～圖6分別示出了系統(tǒng)狀態(tài)變量和滑模變量在3種控制方法下的響應(yīng)曲線(xiàn)。在快速終端滑模控制方法下，系統(tǒng)狀態(tài)經(jīng)過(guò)大約1.7 s到達(dá)滑模面；在指數(shù)型終端滑模控制方法下，系統(tǒng)狀態(tài)1.4 s左右后到達(dá)滑模面；而本文提出的指對(duì)數(shù)型終端滑模控制方法可以保證狀態(tài)到達(dá)滑模面所需的時(shí)間最短，大約為1.2 s。由仿真結(jié)果可知，指對(duì)數(shù)型終端滑模控制的收斂速度快于快速終端滑模控制和指數(shù)型終端滑模控制。

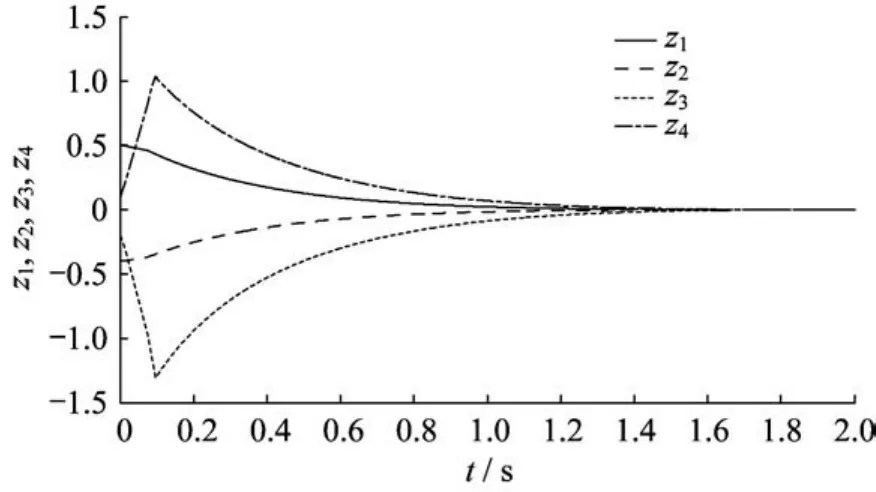
圖1　快速終端滑模狀態(tài)響應(yīng)曲線(xiàn)Fig.1 System state trajectories of FTSMC

圖2　指數(shù)型終端滑模狀態(tài)響應(yīng)曲線(xiàn)Fig.2 System state trajectories of ETSMC

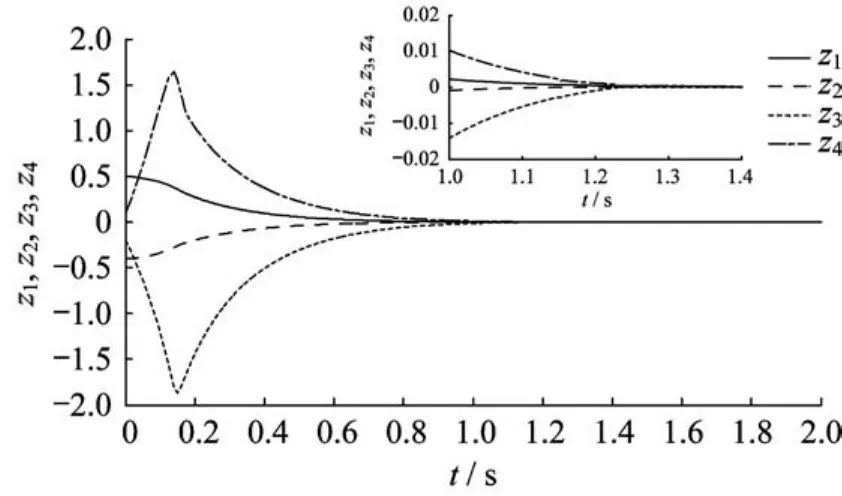
圖3　指對(duì)數(shù)型終端滑模狀態(tài)響應(yīng)曲線(xiàn)Fig.3 System state trajectories of ELTSMC

圖4　快速終端滑模滑模面曲線(xiàn)Fig.4 Sliding variables trajectories of FTSMC

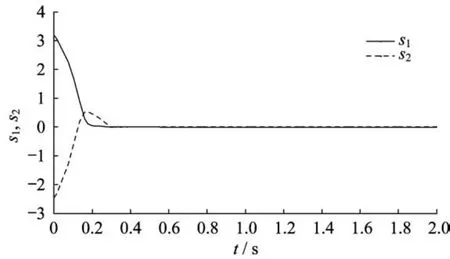
圖5　指數(shù)型終端滑模滑模面曲線(xiàn)Fig.5 Sliding variables trajectories of ETSMC

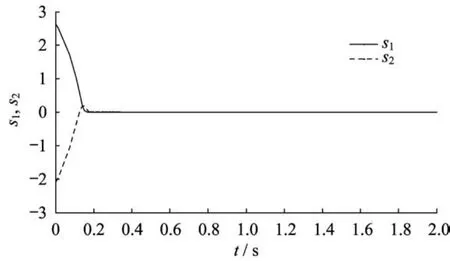
圖6　指對(duì)數(shù)型終端滑模滑模面曲線(xiàn)Fig.6 Sliding variables trajectories of ELTSMC

圖7～圖9示出了3種控制方法下的控制信號(hào)。可以看出，指對(duì)數(shù)型終端滑模控制方法與快速終端滑模控制方法相比，它的控制輸入曲線(xiàn)波動(dòng)要更大一點(diǎn)；但是與指數(shù)型終端滑模控制方法相比，兩者的輸入曲線(xiàn)波動(dòng)就相差不大了。

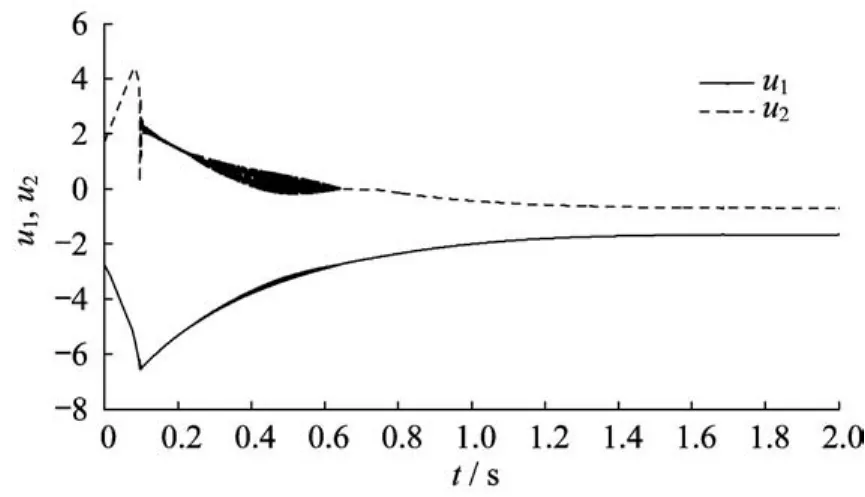
圖7　快速終端滑模控制輸入曲線(xiàn)Fig.7 Control inputs trajectories of FTSMC

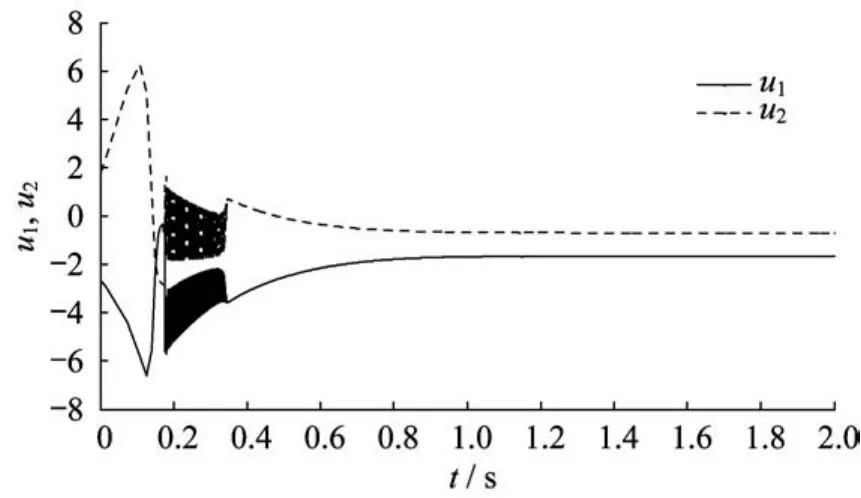
圖8　指數(shù)型終端滑模控制輸入曲線(xiàn)Fig.8 Control inputs trajectories of ETSMC

圖9　指對(duì)數(shù)型終端滑模控制輸入曲線(xiàn)Fig.9 Control inputs trajectories of ELTSMC

5　結(jié) 論

本文研究了不確定MIMO線(xiàn)性系統(tǒng)的終端滑模控制問(wèn)題，提出了新型指對(duì)數(shù)型終端滑模控制方法。能夠保證不確定MIMO線(xiàn)性系統(tǒng)的全局穩(wěn)定性，并使系統(tǒng)狀態(tài)在有限時(shí)間內(nèi)以較快的速度收斂到平衡點(diǎn)，收斂速度快于快速終端滑模控制和對(duì)數(shù)型終端滑模控制方法，同時(shí)對(duì)系統(tǒng)的時(shí)變不確定部分也有較強(qiáng)的魯棒性。但是，相較于快速終端滑模控制方法，指對(duì)數(shù)型終端滑模控制方法的快速收斂性是以控制信號(hào)的增大為代價(jià)的。因此，如何將控制信號(hào)輸入波動(dòng)限定在系統(tǒng)可承受的范圍內(nèi)是下一步工作的重點(diǎn)。

［1］ 張曉字，蘇宏業(yè).滑模變結(jié)構(gòu)控制理論進(jìn)展綜述［J］.化工自動(dòng)化及儀表，2006，33（2）：1-8.

［2］ YU Shuanghe，YU Xinghuo，MAN Zhihong.Robust global terminal sliding mode control of SISO nonlinear uncertain systems［C］//Conference on Decision and Control.Sydney，Australia：IEEE，2000：2198-2203.

［3］ YU Xinghuo，MAN Zhihong.On finite time mechanism：terminal sliding modes［J］.IEEE Workshop on Variable Structure Systems，1996，39（6）：164-167.

［4］ YU Xinghuo，MAN Zhihong.Fast terminal sliding-mode control design for nonlinear dynamical systems［J］.IEEE Transactions on Circuits and Systems，2002，49（2）：261-264.

［5］ 劉云峰，陳斌文，繆棟.具有強(qiáng)魯棒性的滑模變結(jié)構(gòu)控制［J］.信息與控制，2008，37（2）：140-145.

［6］ 張秀華，徐炳林，趙宇.有限時(shí)間收斂的Terminal滑模控制設(shè)計(jì)［J］.控制工程，2008，15（6）：637-639.

［7］ 胡志坤，姜斌，陳沅，等.一種指對(duì)數(shù)型終端滑模控制方法［EB/OL］.［2014-03-10］.http：//jour.blyun.com/views/ specific/3004/CP Detail.jsp？dx Number=330105536887& d=5E8CB01253E72AC13965ABC4EE115C.

［8］ CHEN Syuan-Yi，F(xiàn)AA-Jeng.Robust nonsingular terminal sliding-mode control for nonlinear magnetic bearing system ［J］.IEEE Transactions on Control Systems Technology，2011，19（3）：636-643.

［9］ DAI Weili，DING Jun，TIAN Hao.Nonsingular terminal sliding mode control for voltage regulation system of doubly salient electro-magnetic generator［C］//SICE Annual Conference.Sapporo：IEEE，2014：715-720.

［10］ 李升波，李克強(qiáng)，王建強(qiáng)，等.非奇異快速的終端滑模控制方法［J］.信息與控制，2009，38（1）：18-21.

［11］ 鮑晟，馮勇，鄭雪梅.非匹配不確定MIMO線(xiàn)性系統(tǒng)的終端滑模控制［J］.控制與決策，2003，18（5）：531-539.

［12］ 徐世許，馬建敏.不確定多變量線(xiàn)性系統(tǒng)的快速收斂滑模控制［J］.系統(tǒng)工程與電子技術(shù)，2011，33（7）：1585-1672.

［13］ ZHOU Minghao，F(xiàn)ENG Yong，CHEN Bin.High-order terminal sliding-mode control of uncertain systems with mismatched disturbance［C］//Proceedings of the 32nd Chinese Control Conference.Xi’an，China：2013：3190-3193.

［14］ 劉根旺，李志強(qiáng).非匹配時(shí)變不確定性時(shí)滯系統(tǒng)的Terminal滑模控制［J］.系統(tǒng)工程與電子技術(shù)，2009，31（5）：1180-1183.

An Exponent-Logarithmic Terminal Sliding Mode Control for Uncertain High-Order MIMO Systems

FU Jia-ye， NIU Yu-gang
（Key Laboratory of Advanced Control and Optimization for Chemical Process，Ministry of Education，East China University of Science and Technology，Shanghai 200237，China）

In this paper，an exponent-logarithmic terminal sliding mode control scheme is presented for a class of uncertain high-order MIMO systems.An exponent-logarithmic nonlinear sliding surface is proposed such that the states along the specified sliding surface attain the equilibrium point in finite time with a faster convergence rate.Moreover，a sliding mode controller is designed to guarantee the finite-time reachability of the specified sliding surface.Finally，the simulation results illustrate the effectiveness of the proposed exponent-logarithmic terminal sliding mode control strategy.

terminal sliding mode control；MIMO systems；exponent-logarithmic

TP273

A

1006-3080（2016）01-0085-06 DOI：10.14135/j.cnki.1006-3080.2016.01.014

2015-04-21

國(guó)家自然科學(xué)基金（61273073，61374107）；上海市優(yōu)秀科技帶頭人（14XD1420900）

傅佳燁（1990-），女，浙江寧波人，碩士生，研究方向?yàn)榻K端滑模控制。E-mail：940324037@qq.com

牛玉剛，E-mail：acniuyg@ecust.edu.cn