數字干涉儀時域頻域鑒相性能對比的理論分析

石　榮，李　瀟，鄧　科

(電子信息控制重點實驗室，四川 成都 610036)

?

數字干涉儀時域頻域鑒相性能對比的理論分析

石榮，李瀟，鄧科

(電子信息控制重點實驗室，四川 成都 610036)

基于數字干涉儀中鑒相性能理論分析研究的需要，在對其工作原理簡要概述的基礎上，分別構建了時域和頻域鑒相的數學模型，其中的時域鑒相模型同時也反映出與雙通道互相關處理的等價性。通過鑒相誤差的理論分析，結果表明：2種鑒相方法對干涉儀通道間相位差的估計都具有無偏性；但頻域鑒相相對于時域鑒相，其誤差的方差更小，在低信噪比條件下這一特點表現尤為明顯。理論分析結果與仿真結果完全吻合，從而在理論上證明了頻域鑒相的性能優于時域鑒相，也說明了頻域鑒相性能優于通道間的互相關處理。

數字干涉儀；時域鑒相；互相關處理；頻域鑒相；鑒相性能

0　引言

干涉儀是電子偵察中輻射源來波方向測量的常用設備[1]，不僅可以對雷達信號實施測向[2]，同時也用于通信信號的測向[3]，并以此為基礎來實現對輻射源目標的無源定位[4]。隨著數字化技術的不斷發展，近年來數字式干涉儀(簡稱數字干涉儀)也逐漸替代了模擬體制干涉儀，并成為關注的重點。文獻[5-7]介紹了數字干涉儀的鑒相算法及工程實現；文獻[8]討論了數字干涉儀的基線設計方法；文獻[9]分析了數字干涉儀的測向范圍；文獻[10-12]闡述了數字干涉儀在電子偵察定位中的各種應用方式。由此可見數字干涉儀已在電子戰中廣泛使用，并成為偵察測向的標配設備。

實際上當干涉儀的基線設計一旦確定之后，干涉儀通道間相位差測量的精度將直接決定干涉儀的測向精度，所以數字干涉儀中的數字鑒相方法受到了重點關注。目前主要有2種類型：時域鑒相和頻域鑒相。在當前的工程項目中這2種方法都在不同的場合中使用，但是這2種方法的鑒相精度是各不相同的。文獻[5]通過大量的仿真試驗數據表明：頻域鑒相的精度優于時域鑒相的精度；但并沒有從理論上給予分析與論證，這對于深入理解不同方法產生鑒相精度差異的原因，以及相關的理論模型構建和工程實際應用的指導帶來了不便。

針對這一問題，本文在簡要介紹數字干涉儀的工作原理之后，建立了時域鑒相與頻域鑒相的數學模型，利用此模型對這2種數字鑒相方法所產生的誤差給予了理論公式推導，在鑒相性能對比分析的基礎上，從理論上揭示了頻域方法的鑒相精度優于時域方法的根本原因，最后再次通過仿真驗證了理論分析的有效性。

1　數字干涉儀工作原理

單基線數字干涉儀的工作原理如圖1所示。

圖1　單基線數字干涉儀的工作原理

圖1中，干涉儀天線單元A1,A2之間的距離為d，輻射源目標信號的來波方向與天線陣法向之間的夾角為θ，兩天線接收到的信號經過2路幅相一致性的前端及下變頻通道之后，在中頻進行數字化AD采樣成為數字信號。經過數字鑒相后得到干涉儀兩通道間來波信號的相位差為φ，于是可得如下的測向方程：

(1)

由式(1)可知，在干涉儀基線長度確定的條件下，干涉儀的測向精度完全由通道間的相位差測量精度決定，而相位差測量精度在很大程度上又由數字鑒相環節所影響。目前在數字干涉儀中有2種主要的鑒相方法：時域鑒相和頻域鑒相。

2　時域與頻域鑒相模型

假設與干涉儀天線A1,A2相連的接收通道中加性噪聲互不相關，于是兩接收通道在中頻處的信號可表示成數字解析信號形式如下：xA1(n)=A·exp(j2πfc(n-τ))+

(2)

xA2(n)=A·exp(j2πfcn)+

(3)

式中，A,B分別表示信號與噪聲分量的幅度；fc表示數字采樣條件下的信號載波頻率，在本模型中為已知；nA,c(n)，nA,s(n)，nB,c(n)，nB,s(n)分別表示通道A1,A2中的噪聲，其中每一個噪聲分量的采樣值都可建模為一個均值為0，方差為1的高斯噪聲隨機變量；τ表示采樣條件下2路信號之間的等效時延點數，從時延角度分析可得[13]：

τ=(d·sinθ/c)·fs。

(4)

式中，c表示電磁波傳播的速度；fs表示采樣頻率。于是兩通道間的相位差φ也可表示為：

φ=-2πfcτ。

(5)

2.1時域鑒相模型與時域互相關的等價性

A2exp(-j2πfcτ)=A2exp(jφ)。

(6)

(7)

式中，N2(n)表示通道噪聲的影響，可具體表示為：

N2(n)=ABexp(j2πfc(n-τ))·

ABexp(-j2πfcn)·

(8)

為了消除噪聲的影響，時域鑒相的第2步就是做累積平均，設采樣處理的信號長度為M，于是最終得到的時域鑒相的相位差估計函數Φ3(n)為：

(9)

且有

(10)

但在工程實際應用中，采樣點數M的大小一般是有限的，所以在后續的性能對比中也會在采樣點數M給定的條件下進行理論分析。

2.2頻域鑒相模型

數字干涉儀頻域鑒相過程中首先分別將兩通道的M個采樣數據通過離散傅里葉變換(DFT)轉換到頻域。本文中所采用的DFT的定義式如下：

(11)

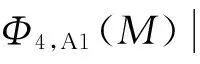
(12)

(13)

(14)

(15)

(16)

式中，angle(?)表示取相位，由于

(17)

3　鑒相性能的對比

前面推導的2種數字干涉儀的鑒相模型，無論是時域鑒相模型，還是頻域鑒相模型，所得到的估計量都是對干涉儀通道間相位差φ的無偏估計量，即估計誤差的均值為0。但2種方法所得到的估計誤差的方差各不相同。下面在相同采樣數據長度M的條件下，來對比2種方法的鑒相性能。

時域鑒相的相位求解表達式為式(9)，其中信號分量的模值為A2；頻域鑒相的相位求解表達式為式(16)，其中信號分量的模值為A。因為2種模型最后都是通過一個綜合性矢量的相位來獲得估計值，所以在性能對比時需要將2種方法在鑒相時的噪聲分量相對于信號分量進行歸一化處理，于是時域鑒相歸一化噪聲分量Nt與頻域鑒相歸一化噪聲分量Nf分別為：

(18)

(19)

經過歸一化處理之后，二者的信號分量都成為單位1。根據前面的分析，Nt與Nf的均值都為0，于是通過計算此時Nt與Nf的方差來反映鑒相性能的好壞。方差越小，性能越好。

2B2/(MA2)+B4/(MA4)。

(20)

(21)

(22)

即時域鑒相誤差的方差始終大于頻域鑒相誤差的方差，即頻域鑒相的性能更好。

對比式(20)和式(21)還可以發現，在采樣數據長度M保持一定的條件下，B相對于A越大，時域鑒相誤差的方差越大，這說明信噪比SNR越低，時域鑒相精度相對于頻域鑒相精度也就越差。

由于鑒相運算的值域范圍被限制在(-π,π]，超出這一范圍將發生相位折疊，所以在信噪比過低條件下，將發生鑒相失效的現象，即鑒相誤差急劇增加。鑒相失效時的信噪比又稱為臨界點信噪比，所以式(20)與式(21)所表示的鑒相誤差的方差是在臨界點信噪比以上時才成立，這一點需要在實際應用中注意。

4　仿真驗證

仿真信號按照式(2)與式(3)來構建，兩通道的初始相位分別為π/3與π/10，顯然通道間的相位差準確值為7/30π，通過不同的B/A條件下的多次蒙特卡羅仿真來統計時域鑒相與頻域鑒相中歸一化誤差的方差，其中數據長度M=1×105。所得到的仿真試驗結果與時域鑒相、頻域鑒相這2種方法中歸一化噪聲分量方差的理論分析結果式(20)與式(21)進行對比。

頻域鑒相與時域鑒相的仿真試驗曲線與理論分析曲線如圖2與圖3所示。

圖2　頻域鑒相噪聲分量方差的理論與仿真曲線對比

圖3　時域鑒相噪聲分量方差的理論與仿真曲線對比

為了在更寬的范圍內來展示結果，所以圖2和圖3中橫坐標采用對數坐標，單位為dB；縱坐標為歸一化噪聲分量的方差。

在圖2和圖3中實線為理論曲線，虛線為仿真曲線，實線與虛線幾乎重合在一起，即理論曲線與仿真曲線完全吻合，從而說明了前面理論分析的有效性和正確性；另一方面對比圖2與圖3可知，在相同的B/A條件下，時域鑒相噪聲分量方差始終高于頻域鑒相噪聲分量方差，這也說明時域鑒相方法所受到的噪聲的影響更嚴重。

為了更加明確地展示這一特點，下面在不同的B/A條件下，通過多次蒙特卡羅仿真來統計時域鑒相與頻域鑒相所得到的干涉儀通道間的相位差誤差的方差曲線如圖4所示。圖4中實線為時域鑒相曲線，虛線為頻域鑒相曲線。

圖4　時域與頻域鑒相所得相位差誤差的方差曲線

此處需要說明的是：上述仿真數據是在數據長度M=1×105的條件下得到的，當數據長度改變時，噪聲分量方差和鑒相所得的相位差誤差的方差的具體數字都會發生變化。但是式(20)與式(21)給出的結果，以及頻域鑒相的性能優于時域鑒相這一結果是不會改變的。

5　結束語

到目前為止，雖然已經有文獻通過仿真試驗和數據統計的方式表明：在電子偵察的數字干涉儀測向應用中，頻域鑒相的精度高于時域鑒相，但是并沒有從理論上給予進一步的分析與證明。針對這一情況，本文分別建立了數字干涉儀的時域鑒相模型與頻域鑒相模型，對2種鑒相方法的鑒相誤差進行了理論分析，展示了2種方法對于通道間相位差估計的無偏性。通過二者的對比可知：在相同的采樣數據長度的條件下，頻域鑒相誤差的方差比時域鑒相更小，這就從理論上解釋了仿真試驗所得到的結果；另一方面，在這一過程也揭示了時域鑒相與雙通道間互相關接收處理的等價性，所以這也同時表明：頻域鑒相方法同樣優于通道間互相關處理方法。上述理論分析過程與相關理論推導結果為數字干涉儀的工程應用設計與理論模型研究提供了重要參考。

[1]MARTINO A D.Introduction to Modern EW Systems[M].USA: Artech House Inc.，2012.

[2]趙國慶.雷達對抗原理(第2版)[M].西安：西安電子科技大學出版社，2012.

[3]POISEL R A.Target Acquisition in Communication Electronic Warfare Systems[M].USA：Artech House Inc，2004.

[4]POISEL R A.Electronic Warfare Target Location Methods (Second Edition)[M].USA: Artech House Inc.，2012.

[5]陳海忠，趙巾衛，朱偉強.數字式干涉儀測向技術鑒相算法研究[J].航天電子對抗，2004，20(4)：30-33.

[6]李莉，朱偉強.數字干涉儀測向實時鑒相技術[J].航天電子對抗，2005，21(2)：51-52.

[7]胡宗愷，饒志宏.高精度數字鑒相技術的FPGA實現[J].通信技術，2010，43(12)：177-179.

[8]羅冰，劉和周，羅進川.基于剩余定理的數字干涉儀設計與實現[J].現代電子技術，2014，37(15)：23-27.

[9]何莉，葉祖昌，張越峰.比相式測向接收機測向范圍分析及仿真[J].現代雷達，2011,33(11)：70-72.

[10]崔玉鑫.多通道數字式干涉儀測向接收機相位校準系統設計[J].艦船電子對抗，2010，33(1)：44-46.

[11]何曉明，趙波.基于數字干涉儀的無源測向技術研究[J].中國電子科學研究院學報，2008，3(5)：460-463.

[12]何曉明，趙波，吳琳.基于數字干涉儀的機載ESM系統實現方法及測向誤差分析[J].艦船電子對抗，2013，36(6)：1-5.

[13]石榮，胡來招.干涉儀測向的時差分析理論及應用[J].航天電子對抗，2012，28(3)：27-30.

石榮男，(1989—)，博士，研究員。主要研究方向：電子對抗，通信、導航與雷達系統等。

李瀟女，(1993—)，碩士研究生。主要研究方向：電子對抗。

Theoretical Analysis on Performance Comparison of Phase Discrimination in Time Domain and Frequency Domain for Digital Interferometer

SHI Rong，LI Xiao，DENG Ke

(ScienceandTechnologyonElectronicInformationControlLaboratory，ChengduSichuan610036，China)

The theoretical analysis and research on performance of phase discrimination for digital interferometer are very necessary.After its working principle is briefly introduced，the mathematic models for phase discrimination in time domain and frequency domain are established respectively.The equivalence between phase discrimination in time domain and cross correlation of two channels can be found easily.The theoretical analysis on the error of phase discrimination has shown that both methods provide non-bias estimations for phase difference between channels，but the error variance of phase discrimination in frequency domain is much less than that of the time domain.This characteristic is more obvious in condition of small SNR (Signal to Noise power Ratio).The theoretical analysis completely fits the simulation.It is theoretically proved that the performance of phase discrimination in frequency domain is much better than that of time domain，and it is also better than that of cross correlation processing of two channels.

digital interferometer；phase discrimination in time domain；cross correlation processing；phase discrimination in frequency domain；performance of phase discrimination

10.3969/j.issn.1003-3106.2016.10.06

2016-06-28基金項目：總裝共用技術基金資助項目(91X0A210XXX1XDZ390XX)。

TN971

A

1003-3106(2016)10-0024-05

引用格式：石榮，李瀟，鄧科.數字干涉儀時域頻域鑒相性能對比的理論分析[J].無線電工程,2016,46(10):24-28.