淺談微積分的應(yīng)用

作者簡介：金韓中（1998.05-），男，韓國人，北京拔萃雙語學(xué)校，高三學(xué)生，拔翠雙語學(xué)校數(shù)學(xué)興趣小組組長。

指導(dǎo)老師：池明月（1981.09-），女，朝鮮族，黑龍江雞西人，北京拔萃雙語學(xué)校教師，從事中學(xué)數(shù)學(xué)教學(xué)，拔翠雙語學(xué)校數(shù)學(xué)興趣小組指導(dǎo)教師。

摘 要：數(shù)學(xué)很好地鍛煉了我們的邏輯思維能力，我們現(xiàn)在能夠運用所學(xué)的數(shù)學(xué)知識解決很多問題。數(shù)學(xué)一直跟隨著科學(xué)社會的進步而發(fā)展，在十七世紀(jì)時，人們面臨著怎樣解決函數(shù)曲線長度的求值問題，曲線圍成圖形面積求值問題，人們借助極限思想，創(chuàng)立了微積分學(xué)，微積分的出現(xiàn)很好地解決了上述問題，并且越來廣泛地應(yīng)用到各個領(lǐng)域中。

關(guān)鍵詞：微分；導(dǎo)數(shù)；定積分；不定積分

中圖分類號：O172文獻標(biāo)志碼：A文章編號：2095-9214（2016）10-0105-02

一、微積分的產(chǎn)生

從17世紀(jì)開始，隨著社會的進步和生產(chǎn)力的發(fā)展，有許多科學(xué)問題需要解決，物理方面的即時速度問題，曲線函數(shù)中曲線長度的求值問題，幾何中曲線圍成圖形的面積求值問題等等，這些促使了新的數(shù)學(xué)思想的產(chǎn)生，“無限細分”以及“無限求和”的思想，最終促使了微積分的產(chǎn)生。

十七世紀(jì)初，有數(shù)十位科學(xué)家對微積分進行了探索，微積分的大量知識已經(jīng)積累起來了。到了十七世紀(jì)后半葉，牛頓主要從運動學(xué)的角度出發(fā)，獨自研究和完成了微積分的創(chuàng)立工作，而萊布尼茨則側(cè)重于從幾何學(xué)的角度出發(fā)，獨自研究和完成了微積分的創(chuàng)立工作，兩人的研究促使了微積分學(xué)的產(chǎn)生。

在十九世紀(jì)以前，在微積分的發(fā)展過程中，其數(shù)學(xué)分析的嚴(yán)密性問題一直沒有得到解決。柯西極限存在準(zhǔn)則為微積分注入了嚴(yán)密性，維爾斯特拉斯，黎曼為積分的完善做出了杰出貢獻。

二、微分的幾何意義及其應(yīng)用

微積分是建立在實數(shù)，函數(shù)和極限的基礎(chǔ)上的，包含微分學(xué)和積分學(xué)。其中微分學(xué)主要包括極限理論，導(dǎo)數(shù)描述，微分等，積分學(xué)主要包括定積分和不定積分。

首先我們要理解到，“極限”在微積分學(xué)中引入的必要性，當(dāng)我們確定一個値時，通過考察這一連串近似值的趨向，確定一連串越來越準(zhǔn)確的近似值，最終確定一個量，這就是極限的思想方法①。

其次，導(dǎo)數(shù)的概念，導(dǎo)數(shù)是指函數(shù)在一點處自由變量所引起的函數(shù)變化的快慢程度。其本質(zhì)是利用極限概念對函數(shù)進行局部的線性逼近。如果函數(shù)的自變量和取值都是實數(shù)的話，函數(shù)在某一點的導(dǎo)數(shù)就是該函數(shù)所代表的曲線在這一點上的切線斜率②。

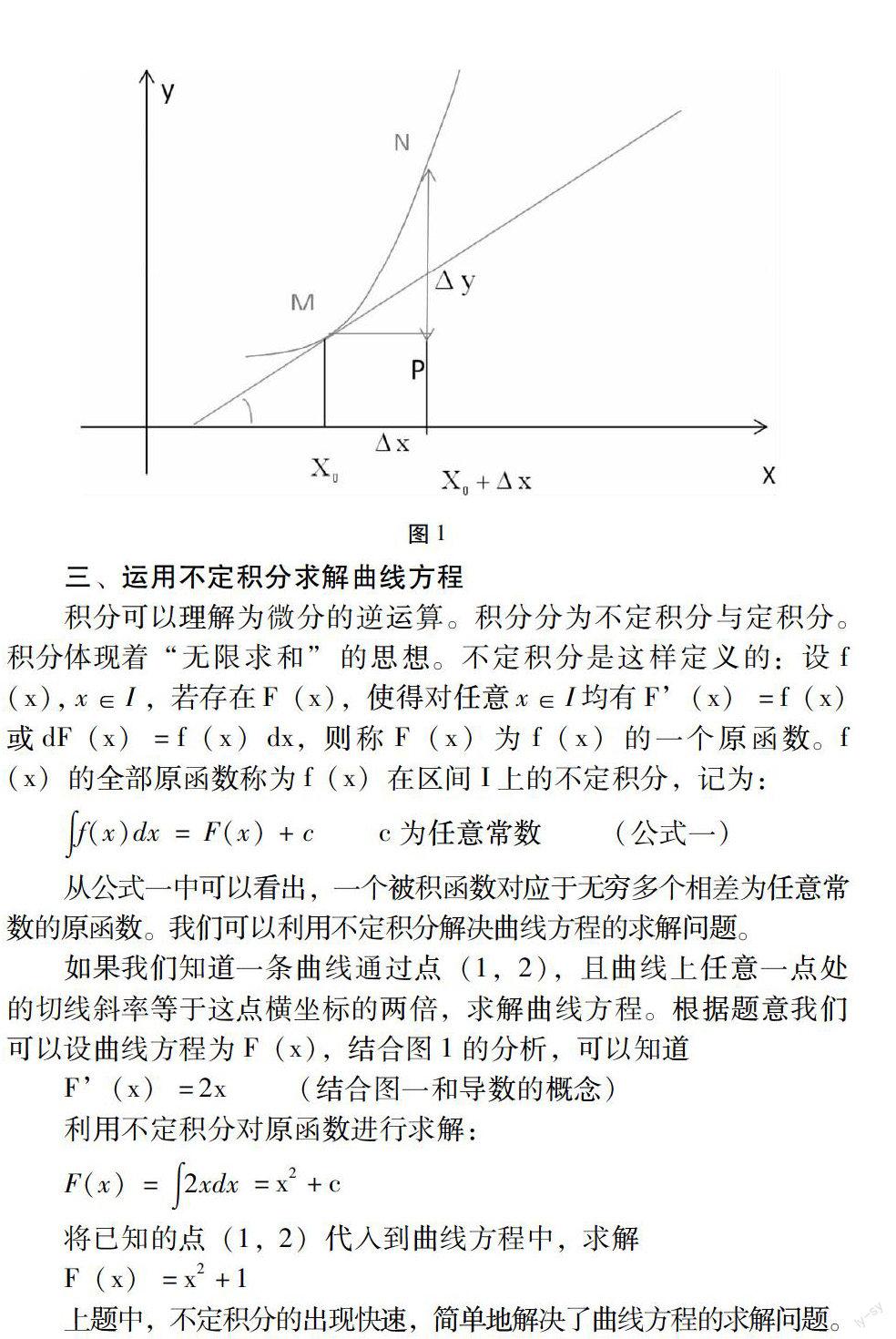
在數(shù)學(xué)中，微分是對函數(shù)的局部變化率的一種線性描述。微分可以近似地描述當(dāng)函數(shù)自變量的取值作足夠小的改變時，函數(shù)的值是怎樣改變的。從微分的幾何意義分析（如圖1），當(dāng)Δy是曲線的縱坐標(biāo)增量時；dy就是切線縱坐標(biāo)對應(yīng)的增量，借助極限思想，當(dāng)Δ x很小時，在點M的附近，切線段MP可近似代替曲線段MN。

從圖一中我們可以看處曲線切線的斜率tanα即為函數(shù)的導(dǎo)數(shù)。

從微分的幾何意義可以看出我們可以利用微分解決求曲線長度的問題。微分也可以利用在物理學(xué)中，如果一個物體的運動路程與時間的函數(shù)為S，則速度函數(shù)是s的導(dǎo)數(shù)，即V=S。

不只是總產(chǎn)量的問題，復(fù)利，年有效收益，連續(xù)復(fù)利，成本函數(shù)，需求函數(shù)，消費者剩余，生產(chǎn)者剩余，最大利潤等一系列的經(jīng)濟問題都可以通過微積分來解決。

六、小結(jié)

從以上例子中，我們看到了微積分在物理學(xué)，在曲線函數(shù)以及經(jīng)濟學(xué)方面的應(yīng)用。微積分是與實際應(yīng)用聯(lián)系著發(fā)展起來的，面對科學(xué)難題，人們開始借助“不變”來認(rèn)識“變”，借助極限的思想，從直線形來認(rèn)識曲線形，從近似認(rèn)識精確。面對變速直線運動的瞬時速度問題，人們借助極限思想，在小范圍內(nèi)，用勻速代替變速，將瞬時速度定義為平均速度的極限，利用微積分解決變速的問題。

在當(dāng)今社會，微積分已經(jīng)越來越廣泛地應(yīng)用到天文學(xué)、力學(xué)、化學(xué)、生物學(xué)、工程學(xué)、經(jīng)濟學(xué)等自然科學(xué)、社會科學(xué)及應(yīng)用科學(xué)等多個分支中。而計算機的發(fā)明更是有助于這些應(yīng)用的不斷發(fā)展。

（作者單位：北京拔萃雙語學(xué)校）

（指導(dǎo)老師：池明月）

注釋：

①對于y=nn+1，當(dāng)n=100時，結(jié)果約為0.99，當(dāng)n=1000時，結(jié)果約為0.999。那么利用極限思想，當(dāng)n無限趨近正無窮，結(jié)果就無限趨近1。即n→+∞，y→1

②運動學(xué)中，做勻加速直線運動的物體在t時刻的運動速度是Vt=V0+at，對Vt求導(dǎo)，可以得到Vt′=a，即物體速度變化的快慢。

參考文獻：

[1]同濟大學(xué)數(shù)學(xué)系.高等數(shù)學(xué)[M].高等教育出版社，2007

[2]龔昇.微積分五講.科學(xué)出版社[M].2004

[3]龔德恩.經(jīng)濟數(shù)學(xué)基礎(chǔ)（微積分）[M].四川人民出版社，2005