明挖地鐵車站主體結構最不利設計水位分析

劉小俊，蔣雅君，馬鵬遠，李　彬，岳　嶺

(1.西南交通大學交通隧道工程教育部重點實驗室，成都　610031；2.中鐵工程設計咨詢集團有限公司，北京　100055)

?

明挖地鐵車站主體結構最不利設計水位分析

劉小俊1，蔣雅君1，馬鵬遠2，李彬1，岳嶺2

(1.西南交通大學交通隧道工程教育部重點實驗室，成都610031；2.中鐵工程設計咨詢集團有限公司，北京100055)

我國華南、華東、華中地區(qū)及沿海城市地下水豐富，地下水壓力是影響地鐵車站主體結構受力的重要因素，隨著水頭高度的變化結構受力會隨之發(fā)生改變。為了研究不同的水位對車站主體結構受力的影響，結合眾多地下水豐富的地鐵工程實例，選取多種水位進行數(shù)值模擬計算，結果表明：影響頂板、中板、底板及側墻的最不利水位并不是統(tǒng)一的水位。為了方便設計，通過將眾多正常使用中的地鐵車站結構受力情況對比分析，認為：選取工程場地內(nèi)最高水位進行車站結構受力計算，然后對部分構件配筋面積進行調(diào)整，能夠滿足車站結構安全的要求。

地鐵車站；明挖法；最不利水位；內(nèi)力分析

1　概述

隨著我國經(jīng)濟的大力發(fā)展，城市化進程的加快，城市人口日漸增多，同時也帶來了諸多的城市問題，如交通擁擠、噪聲污染等。為了能夠有效地解決這些問題，我國加快了城市基礎設施的建設，其中地鐵已經(jīng)成為各大城市主要的交通形式之一[1，2]。在地鐵的建設中，確保車站結構安全可靠至關重要。我國華南、華東、華中地區(qū)及沿海城市地下水豐富，水位較高，一般位于中板以上，地下水壓力是影響地鐵車站主體結構受力的重要因素，并隨著水頭高度的變化結構受力會隨之發(fā)生改變。因此確定工程建設及使用過程中影響結構最不利的水頭高度是非常重要的問題。

《地鐵設計規(guī)范》(GB 50157—2013)規(guī)定：按照可能發(fā)生的地下水最高水位和最低水位兩種情況，計算水壓力和浮力對結構的作用[3]。我國大多數(shù)地鐵車站設計中直接把最高水位當作最不利水位進行結構計算，但這種設計理念存在一定的問題。水位越高，結構所受的軸力和彎矩越大，但并不一定受力最不利。對鋼筋混凝土偏心受壓構件來講，是由軸力和彎矩的組合來確定結構的最不利程度。

通過有限元計算不同水位情況下車站主體結構的內(nèi)力，并分析受力及配筋情況，研究地鐵車站的最不利水位，為地鐵車站設計中水位的選取及如何配筋提供一些可行的建議。

2　工程概述

依托某明挖地下三層車站。該車站圍護結構采用復合式地下連續(xù)墻，車站標準段寬度為15.9 m，高度21.34 m，縱向柱跨9 m，橫向柱跨8 m，頂板、負二層樓板、側墻厚800 mm，負一層樓板厚400 mm，底板厚1 100 mm，柱尺寸為800 mm×1 200 mm。車站覆土計算深度為3.9 m，地勘常水位于地下3 m處。結構形式如圖1所示，土層參數(shù)如表1所示。

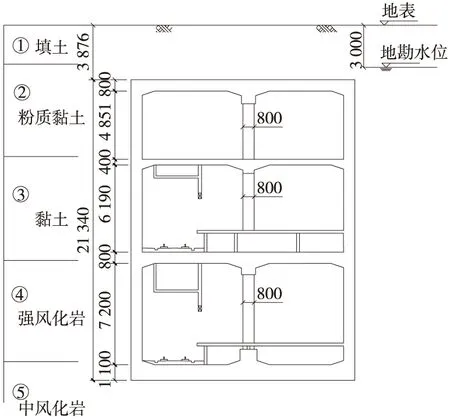
圖1　結構斷面(單位：mm)

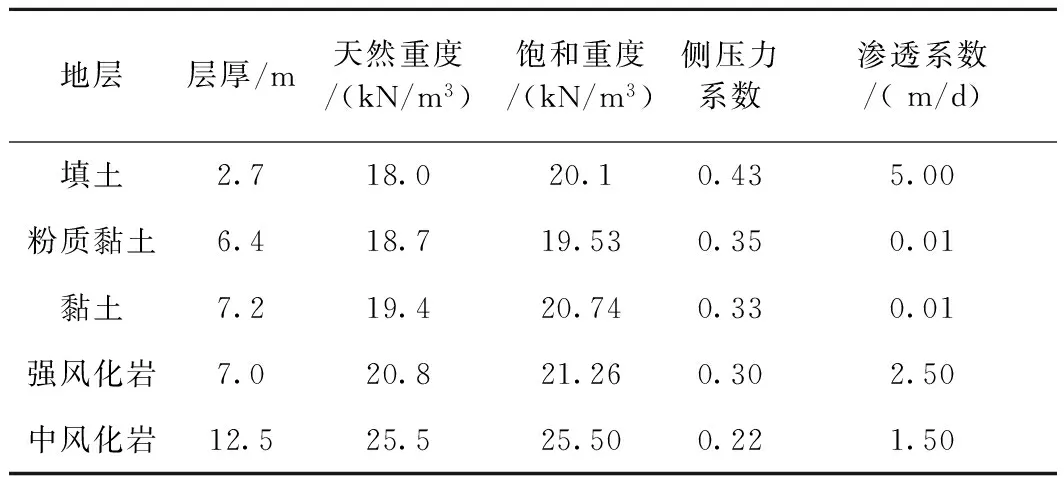
地層層厚/m天然重度/(kN/m3)飽和重度/(kN/m3)側壓力系數(shù)滲透系數(shù)/(m/d)填土2.718.020.10.435.00粉質(zhì)黏土6.418.719.530.350.01黏土7.219.420.740.330.01強風化巖7.020.821.260.302.50中風化巖12.525.525.500.221.50

本場地的地下水按賦存條件主要為第四系孔隙水及基巖裂隙水。孔隙水主要賦存在表層人工填土層，沖洪積層和殘積砂質(zhì)黏性土層中，略具承壓性，基巖裂隙水賦存于強風化及中等風化巖中，具承壓性。采用了5種不同的水位進行計算，水頭高度如表2所示(水位編號5表示最低水位)。

表2　水頭高度

3　數(shù)值計算

采用ANSYS有限元軟件[4，5]分析不同的水位下結構受力情況，以此來分析水位對車站結構的影響。

3.1建立模型

地鐵車站一般為長通道結構，其橫向尺寸遠小于縱向尺寸，因此將其簡化為平面問題求解[6]。將組合成結構的各段梁柱分成梁單元，各單元之間以節(jié)點相連，單元長度縱向取1 m計算(即采用等效剛度法)。圍護結構與主體地下結構采用復合墻相結合的形式[7]，車站的頂板、中板、底板、中柱及側墻均采用梁單元進行模擬。采用彈簧單元模擬地層與結構的相互約束(殺死受拉彈簧)，圍護結構與側墻的作用采用Link10單元(只受壓)模擬，彈性模量數(shù)量級取1015～1017時能較好地保證圍護結構與主體結構變形的協(xié)調(diào)和連續(xù)性[8]。圍護結構底端采用鉸支座進行約束，同時考慮到地下水對結構的浮力，抗浮措施采用抗拔樁，把其底端的水平、豎向位移約束住。

將地層對結構的作用轉化成荷載，采用荷載-結構模型計算，并把圍護結構的剛度折減70%[8]，按長期使用工況(水土分算、土壓力作用在圍護結構上、水壓力作用在主體結構側墻上)，土壓力按靜止土壓力計算，水壓力按靜水壓力計算[8]。計算模型如圖2所示。

圖2　計算模型

3.2荷載計算及組合

結構所承受荷載包括永久荷載、可變荷載，結構計算中選取的荷載種類見表3。根據(jù)《建筑結構荷載規(guī)范》3.2.2條，承載能力極限狀態(tài)應按效應的基本組合或偶然組合(此處僅考慮基本組合情況)進行荷載組合[9]，組合系數(shù)見表4。

表3　荷載種類

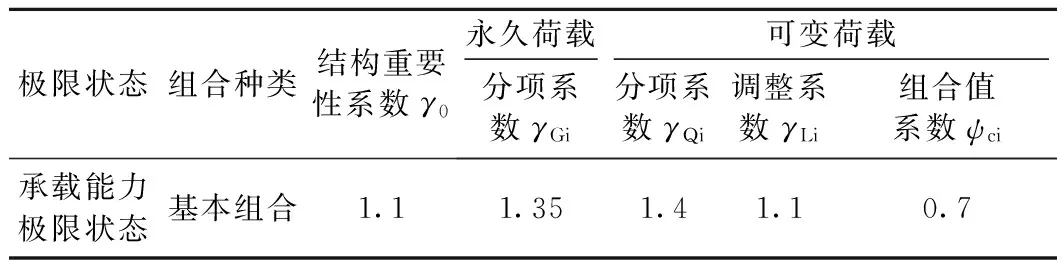
表4　荷載組合系數(shù)

3.3提取內(nèi)力

根據(jù)5種不同水位計算的荷載進行加載計算，并提取不利截面處的內(nèi)力值。橫斷面的不利截面選取如圖3所示。

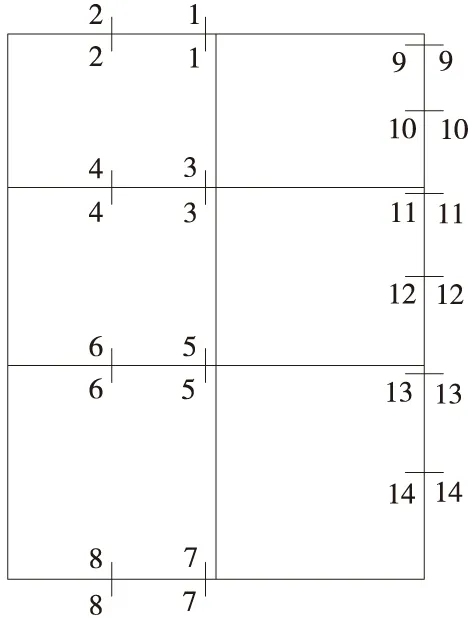
圖3　不利截面的選取位置

4　計算結果及分析

4.1提取內(nèi)力結果

對5種不同水位情況下的計算結果進行比較，分別提取出側墻、頂板、中一層板、中二層板及底板的最大剪力、軸力及彎矩，如圖4～圖6所示。

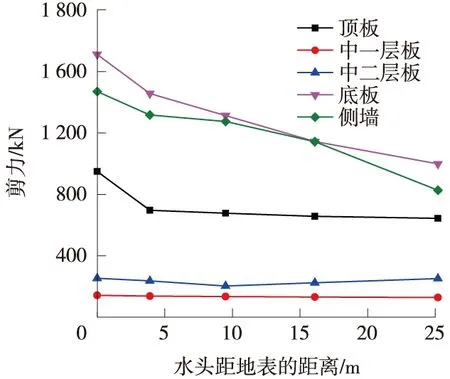
圖4　各板最大剪力隨水頭高度的變化

從圖4可以看出，隨著水位的降低，結構所受的最大剪力減小，底板和側墻尤為明顯。因此應按最高水位計算結構的剪力，按其進行抗剪配筋計算以保證結構抗剪的安全性。

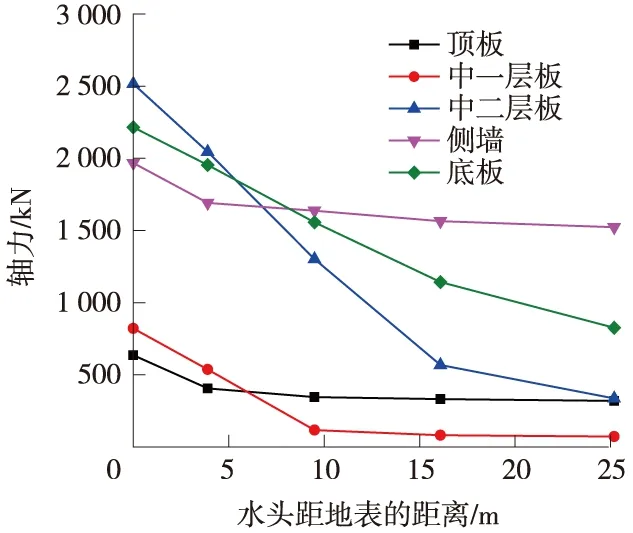
圖5　各板最大軸力隨水頭高度的變化

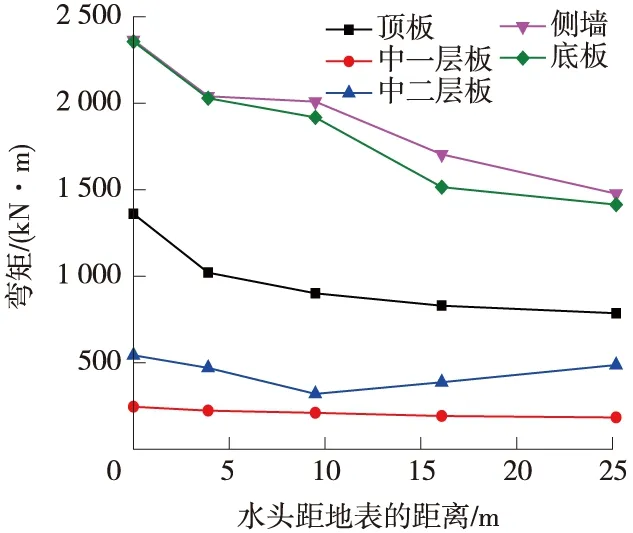
圖6　各板最大彎矩隨水頭高度的變化

根據(jù)各層板跨中部位的受力情況進行分析計算，采用最小配筋率配筋均可滿足要求，因此本文不再研究各層板跨中的受力情況。

從圖5、圖6可以看出，除了中二層板的彎矩隨著水位的降低先減小后增大之外，其他各層板的軸力、彎矩均隨著水位的降低而減小。雖然從圖4、圖5中可以看出，軸力、彎矩基本是隨水位的降低而減小，但混凝土偏心受壓構件正截面承載力是由彎矩和軸力的組合而確定，并不是結構所受的彎矩和軸力最大，結構就最不利。

4.2偏心受壓構件正截面承載能力分析

偏心受壓構件是彎矩和軸力共同作用的構件，軸力與彎矩對于構件的作用效應存在著疊加和制約的關系，即當給定軸力N時，有其唯一對應的彎矩M組合下達到其極限承載能力。

對于偏心受壓短柱、長柱，由其截面承載力的計算分析可以得到圖7所示的偏心受壓構件M-N相關曲線圖。ab段表示大偏心受壓時的M-N相關曲線，為二次拋物線。隨著軸向力N的增大，截面能承擔的彎矩也相應提高。

b點為鋼筋與受壓混凝土同時達到其強度極限值的界限狀態(tài)。此時偏心受壓構件的彎矩M最大。

cb段表示小偏心受壓的M-N相關曲線，是一條接近于直線的二次函數(shù)曲線。由曲線走向可以看出，在小偏心受壓情況下，隨著軸向力的增大，截面所能承受的彎矩反而降低。

在圖7中，c點表示軸心受壓的情況，a點表示受彎構件的情況。圖中曲線上的任一點d的坐標就代表截面強度的一種M和N的組合。若任意點d位于曲線abc的內(nèi)側，說明截面在該點坐標給出的M和N的組合未達到承載能力極限狀態(tài)；若d點位于圖中曲線abc的外側，則表明截面的承載能力不足[10]。

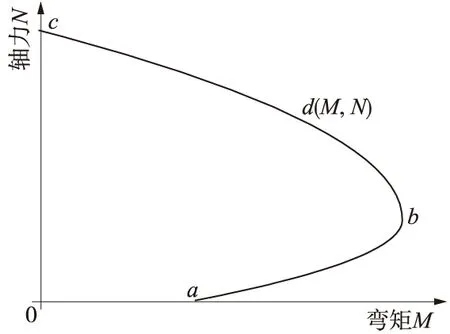
圖7　偏心受壓構件的M-N曲線

采用最高水位計算的軸力、彎矩進行正截面配筋，并繪出每個板的承載能力M-N相關曲線圖。根據(jù)M-N相關曲線圖計算在其他水位情況下的彎矩極限承載力，如圖8所示。

圖8　各層板的彎矩承載力

4.3各層板的不利水位分析

通過計算得出頂板、中板、底板及側墻的安全儲備系數(shù)隨水位的變化，如圖9所示。

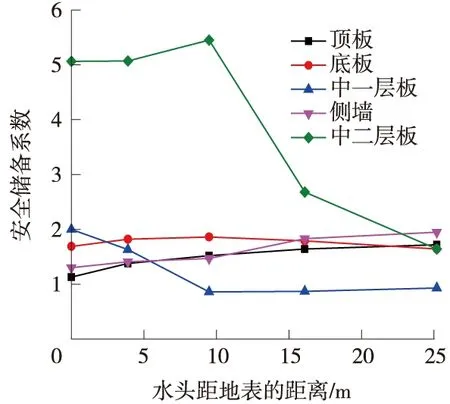
圖9　安全儲備系數(shù)

從圖9可以看出每層板的最不利水位，具體如表5所示。

表5　每層板的最不利水位

由于水對結構的浮力直接作用在底板上，底板的受力受水位的影響比其他部位特殊，因此需單獨分析。從圖8中可以看出最高和最低水位時，底板的安全儲備系數(shù)都比較小，底板受力處于不利狀態(tài)。通過數(shù)值計算，可以得到最高和最低水位下底板所受的彎矩，如圖10、圖11所示。

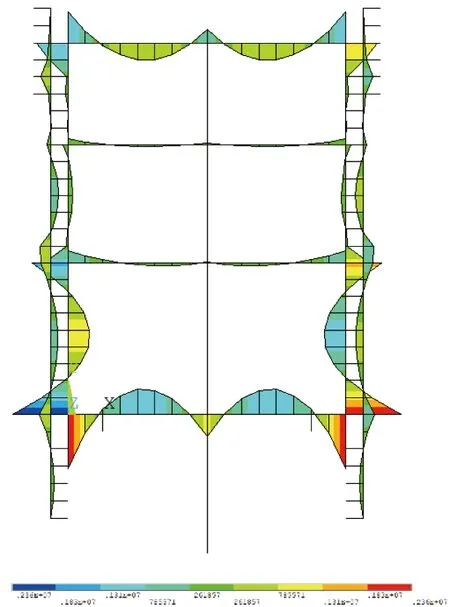
圖10　最高水位彎矩(單位：N·m)

圖11　最低水位彎矩(單位：N·m)

從圖10、圖11可以看出，水位最高和最低時，底板所受彎矩的作用方向已經(jīng)發(fā)生很大的變化，即最高水位和最低水位下，底板的受拉壓區(qū)域已經(jīng)明顯不同。因此最高水位和最低水位都是底板的不利水位。

從配筋的角度出發(fā)，分析不利水位。根據(jù)不同水位下計算的軸力、彎矩進行正截面配筋計算[11，12]，結果見表6。

表6　配筋情況

根據(jù)不同水位計算的配筋量，也可對最不利水位進行一定的判斷，這與安全儲備系數(shù)法得到的結論基本一致。但中二層板在各種水位下用最小配筋率配筋均可滿足要求，所以根據(jù)配筋結果無法得到中二層板的最不利水位。

4.4主體結構的最不利水位分析

本文通過數(shù)值模擬計算不同水位下明挖地鐵車站主體結構的受力，采用安全儲備系數(shù)及配筋法分析得出了頂板、中間板、底板及側墻的最不利水位，發(fā)現(xiàn)并不是統(tǒng)一的水位。每一種結構的最不利水位見表7。

表7　每層板的最不利水位

由表7可以得出，不同的結構部位對應著不同的最不利水位，因此并非水位最高時，結構的受力最不利。如果直接選取最高水位進行結構受力及配筋計算，會造成主體結構的部分結構部位不安全。

《地鐵設計規(guī)范》(GB 50157—2013)規(guī)定按照可能發(fā)生的地下水最高水位和最低水位兩種情況，計算水壓力和浮力對結構的作用。規(guī)范中僅考慮了最高及最低兩種水位對結構的影響，并不能完全反應水位對結構的影響。

但是如果設計人員分別選取每層板的最不利水位進行計算，將會帶來很大的不便。因此從設計者的角度出發(fā)，需確定一個對整體結構最不利的水位進行計算。根據(jù)表6及表7對各層板最不利水位的分析結果，可以把最高水位當作整體結構的最不利水位進行配筋計算，然后再把配筋量做相應的調(diào)整作為最終配筋結果。這樣既可以保證結構的受力安全又可以提高設計者的計算效率。根據(jù)表6的配筋計算結果，結構的底板按最高水位計算出受拉側鋼筋面積，并且受壓側的鋼筋面積取與受拉側相等；中間層板按最高水位計算出配筋以后，將受拉側鋼筋面積乘以1.5系數(shù)，受壓側不需調(diào)整；側墻及頂板按最高水位計算進行配筋，以此作為最終計算配筋結果。

5　結論

本文通過對不同水位下明挖地鐵車站主體結構的受力分析，得出了頂板、中間板、底板及側墻的最不利水位并不是統(tǒng)一的水位。但是為了提高設計者的工作效率，提出明挖地鐵車站整體結構的最不利計算水位，即最高水位。

(1)根據(jù)最高水位計算結構各層板的剪力，進行抗剪配筋計算。

(2)頂板、側墻直接根據(jù)最高水位計算軸力和彎矩，進行正截面承載配筋計算。

(3)底板根據(jù)最高水位計算受拉側鋼筋面積，并且受壓側的鋼筋面積取與受拉側相等進行配筋。

(4)中間層板根據(jù)最高水位計算出配筋，將受拉側鋼筋面積乘以1.5系數(shù)，受壓側不需調(diào)整，以此作為最終計算配筋結果。

根據(jù)本文得出的結論進行車站設計計算，既能提高設計者的效率又能保證結構的安全，希望能夠對明挖地鐵車站最不利水位的選取提供參考；同時本文也存在不足之處，本文采用平面等效剛度簡化計算，雖然這種方法目前得到了廣泛應用，但問題存在于：將縱梁和板、柱分離開進行計算，使整個結構的變形協(xié)調(diào)條件得不到滿足，導致板、縱梁內(nèi)力與實際有所不符[13-15]。

[1]汪勝.城市軌道交通工程規(guī)劃方案研究的必要性及研究內(nèi)容探討[J].鐵道標準設計，2015(3)：1-6.

[2]胡智民.地鐵車站、車輛基地綜合開發(fā)設計技術研究[J].鐵道標準設計，2014，58(7)：145-148.

[3]中華人民共和國住房和城鄉(xiāng)建設部.GB 50157—2013地鐵設計規(guī)范[S].北京：中國建筑工業(yè)出版社，2014.

[4]王新敏.ANSYS工程結構數(shù)值分析[M].北京：人民交通出版社，2007.

[5]李圍，冼進.隧道及地下工程ANSYS實例分析[M].北京：中國水利水電出版社，2007.

[6]王艷芳，范明橋，周密.明挖地鐵車站深基坑有限元分析與模擬[J].現(xiàn)代交通技術，2015(6)：72-75.

[7]徐向輝.明挖地鐵車站疊合墻與復合墻方案比選[J].鐵道標準設計，2005(12)：77-80.

[8]蔣雅君，邱品茗.地下工程本科畢業(yè)設計指南[M].成都：西南交通大學出版社，2015.

[9]中華人民共和國住房和城鄉(xiāng)建設部.GB 50153—2012建筑結構荷載規(guī)范[S].北京：中國建筑工業(yè)出版社，2012.

[10]葉見署，李國平.結構設計原理[M].北京:人民交通出版社，2005.

[11]中華人民共和國住房和城鄉(xiāng)建設部.GB 50010—2010混凝土結構設計規(guī)范[S].北京：中國建筑工業(yè)出版社，2010.

[12]宋儀.地鐵明挖車站有關配筋問題的探討[J].隧道建設，2012，32(4)：514-517.

[13]王博.明挖地鐵車站整體建模結構受力分析[J].鐵道標準設計，2012(11)：75-79.

[14]李延，漆泰岳.地鐵車站結構設計中空間效應的影響[J].現(xiàn)代隧道技術，2015(5)：138-144.

[15]代坤.明挖地鐵車站空間計算模型與平面計算模型的對比分析[J].四川建筑，2011，31(1)：126-128.

Analysis of Most Unfavorable Design Water Level of Open-and-cut Metro Station Main Structure

LIU Xiao-jun1， JIANG Ya-jun1， MA Peng-yuan2， LI Bin1， YUE Ling2

(1.Key Laboratory of Southwest Jiaotong University Transportation Tunnel Engineering of Ministry of Education，Chengdu 610031, China; 2.China Railway Engineering Consulting Group Co., Ltd， Beijing 100055, China)

In Southern China， East China， Central China and coastal cities， groundwater pressure is an important factor affecting the main structure of the subway station. With the change of the water head height， the structure stress is also changed. In order to study the effect of different level on the station main body structure， this article， with reference to variety of water-rich metro engineering cases， selects different water level many for numerical simulation and calculation. The results show that the most unfavorable water level affecting the top plate， the middle plate， the bottom plate and the side wall is not uniform. In order to facilitate the design， the article， based on the stress analysis of a large number of subway station structures in normal service， concludes that the highest level of the station structure is selected to calculate structure stress， and then adjust the area of reinforcement of partial components so as to meet the requirements for the safety of station structures.

Metro station; Cut and cover method; Most unfavorable water level; Internal force analysis

2016-01-04；

2016-02-27

中央高校基本科研業(yè)務費專項資金資助(SWJTU11ZT33)，中央高校基本科研業(yè)務費專項資金資助(2682014CX065)

劉小俊(1990—)，男，碩士研究生，E-mail：15680757153@163.com。

1004-2954(2016)09-0113-05

U231+.4

ADOI:10.13238/j.issn.1004-2954.2016.09.025