基于灰色模型的我國民用住宅建筑面積占比預測
張躍

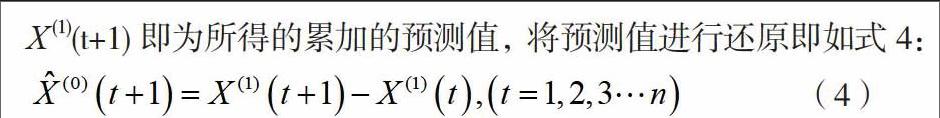

摘 要:為了預測我國民用住宅建筑面積占比,根據我國2015年的中國統計年鑒,通過利用2004-2013年我國民用住宅建筑面積占比的原始數據,運用曲線擬合法以及GM(1,1)灰色關聯的辦法預測我國2014年民用住宅建筑面積占比,并且與真實的2014年民用住宅建筑面積占比進行誤差比較,計算結果表明運用灰色關聯的辦法得到的預測數據更加準確。
關鍵詞:灰色模型;建筑面積占比;民用住宅
我國民用住宅建筑面積占比對于國民經濟的發展以及城鎮化建設的發展有非常重要的作用,因此如何可靠地準確預測我國民用住宅建筑面積占比一直是廣受關注的問題。文章主要依據我國2015年的中國統計年鑒中我國建筑面積的統計數據,運用灰色理論作為基礎,在此基礎上建立我國民用住宅建筑面積占比的GM(1,1)灰色模型,并運用曲線擬合法擬合了二次曲線模型,用兩種方法對我國民用住宅建筑面積占比進行了預測,并與真實值做出對比,得到兩種方法的預測誤差。
1 灰色理論基本模型
灰色關聯理論是我國著名學者鄧聚龍教授于上個世紀80年代提出,對于灰箱問題,已知一部分的信息,但對其運行機理并未完全明確,可以運用灰色理論進行預測。灰色理論是根據已知的部分信息,建立一個從已知進一步預測未知的GM模型,因此預測某一系統中的可能出現的變化趨勢,為相關的決策規劃做出相對應的參考。在灰色關聯理論中,對于時間序列的參數化預測,增加了其確定性,而削弱了其隨機性,此時在已知層上進行求解得到相關的預測函數,并且據此對對應的序列進行相關的預測,該預測模型為一個一階微分方程,是一個僅為一維變量的灰色模型,因此被記作GM(1,1)灰色模型。
GM(1,1)灰色模型在計算當中是對矩陣進行計算,因此運用相對應的計算軟件可以高效的對GM(1,1)灰色模型的預測結果進行計算。在計算過程中,GM(1,1)灰色模型是一個一階微分方程的模型,它的離散時間的相關相應函數是類似于指數函數進行呈現,對GM(1,1)灰色模型進行構建的具體辦法如下:
首先設定一個已知原始的非負得時間序列為X(0)={X(0)(1),X(0)(2),X(0)(n)},并且設定累加生成的序列為X(1)(t),計算方法如式1:
(1)
GM(1,1)模型的白化微分方程如式2:
(2)
在上式當中,a為待辨識參數,稱為發展系數;u為待辨識內生變量,也稱為灰作用量.設待辨識向量,按最小二乘法求得式中
因此可得到灰色預測的離散時間響應函數為式3:
(3)
X(1)(t+1)即為所得的累加的預測值,將預測值進行還原即如式4:
(4)
2 模型預測
依據中國統計年鑒中我國建筑面積的統計數據,將2005年到2014年的10年我國民用住宅建筑面積占比作為基本數據,數據值如表1所示,根據表1的數據,對2005年-2013年我國民用住宅建筑面積占比建立曲線擬合的模型以及GM(1,1)灰色模型,分別運用兩種方法對我國2014年民用住宅建筑面積占比作出預測。
2.1 曲線擬合法
運用曲線擬合法對2005年-2013年我國民用住宅建筑面積占比建立二次曲線模型,所得到的二次曲線模型如圖1所示
所得到的二次曲線預測模型公式為:y=-0.0028x2+ 11.311x–11346。根據所得到的二次曲線模型對2014年民用住宅建筑面積占比作出預測,預測得到的預測值為77%,這與實際數據的71.91%有較大的誤差,相差值為7%。
2.2 灰色預測
運用灰色理論對2005年-2013年我國民用住宅建筑面積占比建立GM(1,1)灰色模型,根據GM(1,1)灰色模型對2014年民用住宅建筑面積占比作出預測,運用灰色關聯模型預測得到的預測值為73.96%,這與實際數據的71.91%相比誤差較小,相差值為2.8%。
3 結語
運用灰色關聯模型以及曲線擬合模型對我國民用住宅建筑面積進行預測,計算結果表明,運用灰色關聯模型計算所得到的模型較為準確,說明灰色關聯模型在進行相對應系統的預測有較好的預測效果。
參考文獻
[1] 胡坤.灰色預測評價方法與應用研究[D].南京航空航天大學,2004.
[2] 周小俊,田金國,谷川.灰色關聯預測及其在變形預測中的應用[J].鐵道勘察,2009(01).
[3] 曾波,劉思峰.基于灰色關聯度的小樣本預測模型[J].統計與信息論壇,2009(12).

