原子力顯微鏡探針懸臂彈性常數(shù)校正技術(shù)進展

屈澤華，卜　娟，潘曉霞

（聚合物分子工程國家重點實驗室，復(fù)旦大學(xué)高分子科學(xué)系，上海 200433）

原子力顯微鏡探針懸臂彈性常數(shù)校正技術(shù)進展

屈澤華，卜娟，潘曉霞

（聚合物分子工程國家重點實驗室，復(fù)旦大學(xué)高分子科學(xué)系，上海 200433）

利用原子力顯微鏡對材料表面的力學(xué)性能進行定量表征時，需要準確知道原子力顯微鏡探針懸臂的彈性常數(shù)，所以對彈性常數(shù)進行校正十分重要。該文綜述近年來對探針懸臂彈性常數(shù)的校正方法，主要包括維度法、靜態(tài)撓度法、動態(tài)撓度法。維度法對不同懸臂形狀（主要針對矩形、V型）進行闡述，分析不同方法使用的數(shù)學(xué)模型與優(yōu)缺點；靜態(tài)撓度法不僅對方法的數(shù)學(xué)模型進行闡述，還著重介紹近年來對該方法精確度的改進研究；動態(tài)撓度法以附加質(zhì)量法、Sader法與熱調(diào)諧法分別闡述，比較3種方法的模型特點與先進性；最后分析常用探針適合使用的校正方法，對今后校正方法的發(fā)展提供參考。

探針懸臂；彈性常數(shù)；校正；綜述

0　引　言

原子力顯微鏡發(fā)展到今天，人們已經(jīng)不再局限于僅用其實現(xiàn)對材料表面的顯微成像，而是更多地關(guān)注其對物化性能的檢測，對力學(xué)性能的表征便是其一[1-2]。原子力顯微鏡在進行力學(xué)表征時是通過測定探針與樣品表面的相互作用的力曲線實現(xiàn)的。在測定力-位移曲線時，檢測的探針與樣品之間的作用力即微懸臂的彈力，它遵循Hooke定律：F=-Kδc（K為微懸臂的彈性常數(shù)，δc為微懸臂的偏移量）。要想獲得準確的探針與樣品之間的作用力，必須知道懸臂的彈性常數(shù)，懸臂的彈性常數(shù)不僅影響原子力顯微鏡測定力的大小，還影響探針的掃描速度以及掃描圖像的質(zhì)量，通常市售探針盒上會標注一個供參考的彈性常數(shù)，但是由于懸臂梁的制作工藝造成每根探針的彈性常數(shù)都不同，都與標注值有偏差，所以，在定量表征力學(xué)性能前必須先對彈性常數(shù)進行校正[3]。本文將針對近年來探針懸臂彈性常數(shù)校正方法的研究進展作詳細綜述。一般來講，校正探針懸臂彈性常數(shù)的方法可歸結(jié)為維度法、靜撓度測量法和動撓度測量法3種方法。

1　維度法

通常原子力探針懸臂的形狀主要分為兩種：矩形和V型。維度法對于矩形探針模型比較容易建立，彈性常數(shù)可以通過加載在懸臂自由端時沿著光束的力來計算。通過假定一個小的垂直的反射量Z，用下式[4]計算：

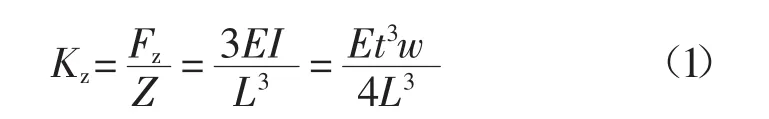
式中：L、w、t——懸臂的長度、寬度和厚度；

E——楊氏模量；

Fz——加載的力；

I——矩形梁的慣量。

V型懸臂由于被認為具有更高的側(cè)向剛度是目前探針形狀里面較流行的設(shè)計[4]，但對于V型探針，不同廠家的設(shè)計形狀略有不同，有些還有金屬涂層。這些因素都影響懸臂的彈性常數(shù)，也造成彈性常數(shù)計算方法的不同。

維度法計算V型懸臂的方法主要有3種：1）平行光束近似法；2）復(fù)雜的分析模型；3）有限元分析法。

1.1平行光束近似法

平行光束近似法是將V型懸臂近似地看作兩個矩形梁平行連接組成。Butt等[5]基于這個假設(shè)對式（1）進行改進，但是由于實際兩個“矩形梁”并非平行，而是斜交的，因此計算方法會帶來一定的誤差，當(dāng)懸臂的長L比較短且懸臂自由端成一條直線時，這種假設(shè)更加準確，但是當(dāng)懸臂的長L比較長的時則Albrecht模型公式則更為準確[6]。為了讓模型更加有效而準確，Sader等[7]在數(shù)學(xué)模型中引入了V型懸臂頂角2θ（如圖1（a）所示）。下面列舉4個最典型的平行光束近似法的簡單模型公式。

圖1　V型懸臂示意圖

Butt模型[5]：

Albrecht模型[6]：

Sader模型[7]：

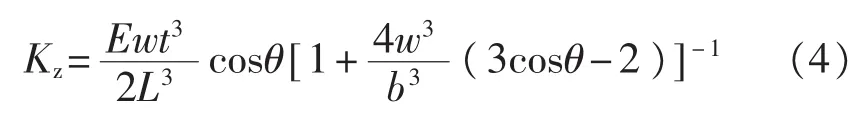
1.2復(fù)雜分析模型

復(fù)雜分析模型的中心思想是將懸臂看成兩個或兩個以上的形狀，并且引入更多的元素。復(fù)雜模型也適用于懸臂成A字形狀的探針，比如Warmack闡述的計算模型[8]如式（5）所示，模型中懸臂幾何尺寸參數(shù)的意義如圖1（b）所示，此計算方法需要已知懸臂尺寸、針尖的位置和楊氏模量。如果L1和針尖到懸臂頂端的距離d設(shè)定為0，則彈性常數(shù)可以簡化為下式，成為簡單模型。

Tortonese把懸臂尖端尺寸分出如圖1（b）所示的L2的區(qū)域，并標示通過懸臂梯形兩腰延長線的交點與懸臂底端平行的線的長度e，引出另外一個式（7）[9]。對于一個V形懸臂（見圖1（a）），該寬度等于2w。Tortonese方程同Warmack方程在當(dāng)懸臂假定為V型，同時d為0時具有一致的結(jié)果。

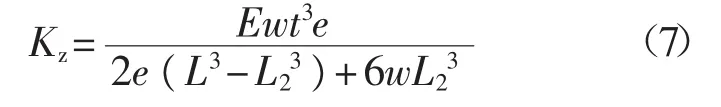
1.3有限元分析

90年代初已有利用有限元分析（FEA）方法模擬V形懸臂的報道。這種方法要求精確知道懸臂幾何形狀、楊氏模量還有懸臂梁的密度。該方法的優(yōu)點是簡單、快速，可以將涂層與基體視為一個平均材料處理各種帶有不同涂層的V形懸臂。近年對該方法的研究大多是將有限元的方法結(jié)合到其他方法中提高彈性常數(shù)的精確度[3，10]。

維度法直觀明了，主要基于對探針的幾何尺寸和彈性性能的測試。維度法針對直角懸臂的計算準確度較高，但對于V型、A型、梯形或者更加復(fù)雜的形狀精確度不高。

2　靜態(tài)撓度法

靜態(tài)撓度法即參考懸臂法，主要通過準確校正一個參考懸臂，然后使用這個參考懸臂校準未知的懸臂梁，如圖2[11]所示。

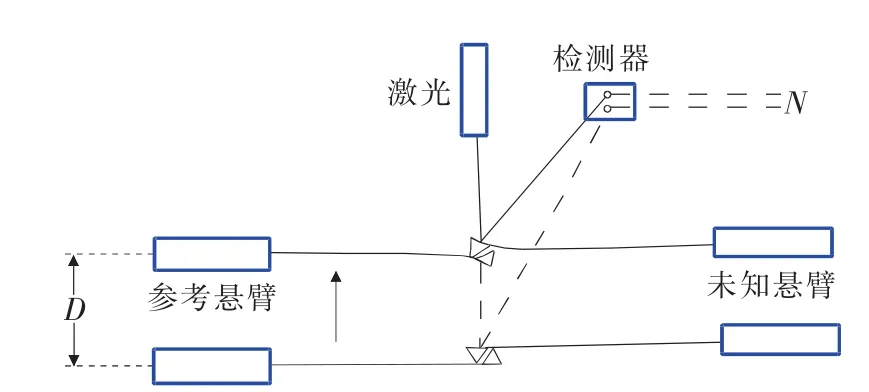
圖2　參考懸臂法校正彈性常數(shù)的示意圖

未知彈性常數(shù)的探針懸臂（右側(cè)）壓在已知彈性常數(shù)的參考懸臂（左側(cè)）上，通過測定兩個懸臂的偏轉(zhuǎn)靈敏度，即可得出未知懸臂的彈性常數(shù)，如下式所示：

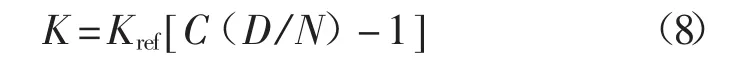
式中：Kref——參考懸臂的彈性常數(shù)；

C——nA與nm的轉(zhuǎn)化系數(shù)；

D/N——在力曲線接觸區(qū)域的斜率的倒數(shù)。

參考懸臂法由于其測試方法簡單快速，測試結(jié)果準確性較高等優(yōu)點使用廣泛，近年來不斷有研究人員對方法進行改進。Richard S.Gates等[12]對參考懸臂梁的外端荷載進行了修正。通過Hooke定律結(jié)合Euler-Bernoulli光束方程得到下式：

式中：Kref、L——參考懸臂的彈性常數(shù)和長度；

ΔL——端部到承載位置的距離（如圖3所示）；

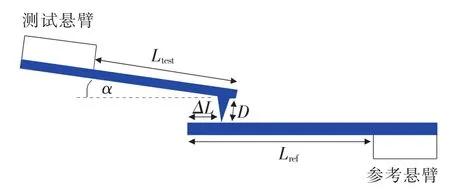
圖3　Gates改進參考懸臂數(shù)學(xué)模型的參數(shù)意義

cos2α——懸臂傾斜角度的幾何校正；

Sref——測試懸臂壓在參考懸臂上的光桿靈敏度；

Shard——測試懸臂梁壓在堅硬的表面（如硅等）的光桿靈敏度。

實際上，參考懸臂法的準確度主要依賴于參考懸臂本身彈性常數(shù)測量的準確性，因此，近年來對該方法的改進集中在提高對參考懸臂彈性常數(shù)的測量準確度上。Clifford等[13]采用納米壓痕儀首先校正參考懸臂的彈性常數(shù)，獲得更加準確的參考懸臂的彈性常數(shù)值，再對未知懸臂做進一步檢測，提高了本方法的準確度，其方法具體的表達式為

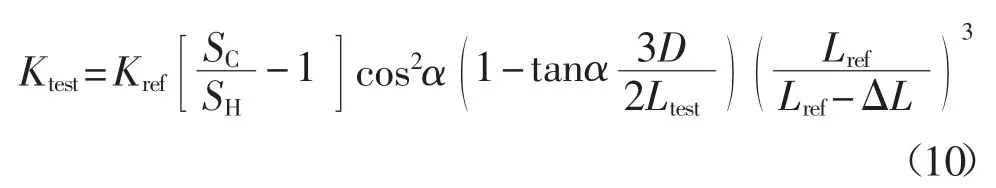
式中：SH——未知懸臂梁壓在堅硬表面的光桿靈敏度；

SC——未知懸臂梁壓在參考懸臂梁時的光桿靈敏度；

D——未知懸臂投影的高度（如圖3所示）；

Kim等[14]把校準的懸臂連接到一個固定的支架上，支架由一個高準確度掃描儀（重力方向1nm分辨率）記錄位移。懸臂被壓在一個精密質(zhì)量比較器的負載按鈕上。將彈性壓縮懸臂所產(chǎn)生的力再由一個電磁力補償，從而保持負載按鈕的位置。補償力等于接觸力，懸臂的彈性常數(shù)通過其位移除以電磁力來確定。懸臂的位移測量由一個電容傳感器納入掃描儀中，由激光干涉儀校準。這種被稱為納米力的校準方法可提供更加準確的測定，對MP31120探針不確定性不到1%。

Ashley D Slattery等[15]使用聚焦離子束在參考懸臂上制造小孔進行位置標記，再利用Clifford方法校正彈性常數(shù)，同樣，也提高了該方法的不確定性。

3　動態(tài)撓度法

3.1Cleveland方法（附加質(zhì)量法）

1993年，Cleveland[4]通過將已知質(zhì)量的物質(zhì)如微球等附加到懸臂的自由端，然后測量附加質(zhì)量前后共振頻率的變化獲得彈性常數(shù)。其彈性常數(shù)的計算為

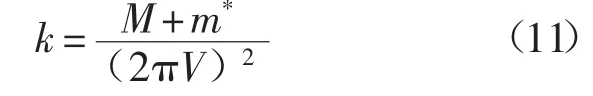
式中：m*——有效的懸臂質(zhì)量；

M——附加在懸臂末端的質(zhì)量；

V——懸臂的共振頻率。

如果測量得到空載諧振頻率V0及附加質(zhì)量M1的諧振頻率V1，則可以根據(jù)已知得到質(zhì)量、頻率、彈性常數(shù)的關(guān)系方程：

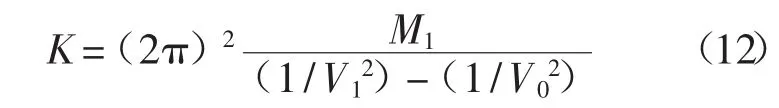
式（12）還可以轉(zhuǎn)變?yōu)閺椥猿?shù)與懸臂尺寸、密度、模量和諧振頻率的關(guān)系式：

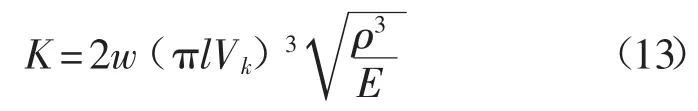
式中：w——懸臂梁的寬度；

l——懸臂梁的長度；

Vk——諧振頻率；

ρ——懸臂密度；

E——彈性模量。

利用Cleveland計算方法推導(dǎo)出的扭轉(zhuǎn)彈性常數(shù)的計算式[16]為

式中：KΦ——扭轉(zhuǎn)彈性常數(shù)；

ωt——扭轉(zhuǎn)共振頻率；

Je——有效的質(zhì)量矩。

并得到當(dāng)附加物為球型時的扭轉(zhuǎn)彈性常數(shù)的計算公式：

式中ρs和r分別為附加物的密度與半徑。

3.2Sader方法

Sader方法[17]是通過在已知密度和粘度的流體場（如空氣）中微懸臂梁振動的諧振響應(yīng)過程中加入流體耗散效應(yīng)計算彈性常數(shù)的方法。對于直角懸臂，有：

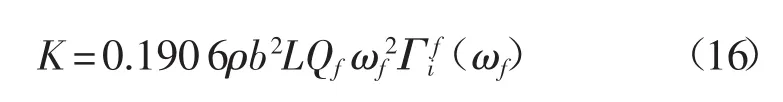
式中：L、b——懸臂的長和寬；

ρ——流體的密度；

ωf——徑向的振動頻率；

Qf——諧振峰的品質(zhì)因子；

Γi——流體函數(shù)的虛部。

Γi是雷諾茲數(shù)Re的函數(shù)。懸臂的諧振頻率ω和品質(zhì)因子Q值可以通過懸臂熱驅(qū)動的振蕩功率譜密度分析得到，基本功率譜共振峰通過擬合一個簡諧振子的響應(yīng)加白噪聲基底得到[18]，其計算表達式為

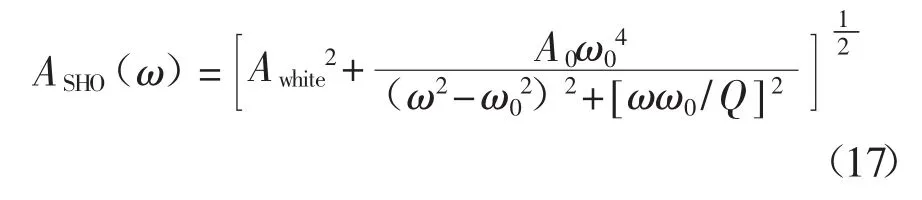
式中：Awhite——白噪聲基底振幅；

A0——零頻率振幅；

ω0——無耗散效應(yīng)的諧振頻率；

Q——品質(zhì)因子。

Sader等將Sader方法進行拓展，推導(dǎo)出了Sader扭轉(zhuǎn)彈性常數(shù)的公式：

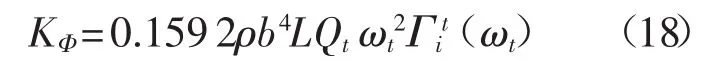
經(jīng)實驗驗證，Sader扭轉(zhuǎn)彈性常數(shù)公式與Cleveland扭轉(zhuǎn)彈性常數(shù)公式計算結(jié)果高度一致[16]。

Sader等[19-21]最近還提出了對Sader公式的簡化。簡化方法僅依靠懸臂的共振頻率和品質(zhì)因數(shù)，不需要測量懸臂梁的動力學(xué)性能，更加省時實用。經(jīng)過驗證，該簡化方法同樣準確、快速。

Sader還在網(wǎng)站上（http://www.ampc.ms.unimelb. edu.au/afm/calibration.html）提供了一個Java小程序，只要輸入懸臂的長度和寬度，適當(dāng)?shù)闹C振頻率和相應(yīng)的質(zhì)量因子，按計算按鈕，就可以自動執(zhí)行計算，在線校正彈性常數(shù)。

3.3熱噪音法

熱噪音（或稱熱調(diào)諧、熱振動）法是目前最流行和最廣泛使用的方法之一。Vecco公司所有使用V型控制器的系統(tǒng)都用熱噪音法進行校正。熱噪音法是根據(jù)分子熱運動理論，把懸臂梁近似等效成理想彈簧，懸臂當(dāng)作一個簡單的諧波振蕩器，測量微懸臂梁的位移隨著時間的變化，通過微懸臂處于熱平衡狀態(tài)時的熱噪音譜，獲得彈性常數(shù)與溫度、噪聲譜之間的關(guān)系，從而求出微懸臂的法向彈性常數(shù)[22]。

熱噪音法的基本數(shù)學(xué)模型公式為

式中：KB——波爾茲曼常數(shù)（1.38×10-23J/K）；

T——絕對溫度；

〈Zc2〉——懸臂位移的均方根。

考慮到懸臂不是理想彈簧，他們振蕩模式的能量不同于一個簡單的諧波振蕩器。所以引入校正因子，公式變?yōu)?/p>

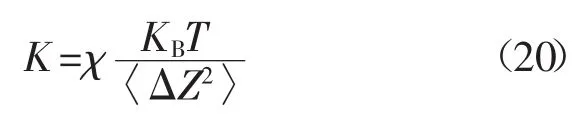
式中：〈ΔZ2〉——懸臂自由端位移的均方根；

χ——校正因子。

校正因子依賴于探針懸臂的形狀和激光聚焦在懸臂上面的位置[23-24]。

為了提高探針與樣品間的距離，原子力顯微鏡的懸臂通常安裝在與水平有很小角度的位置。校準的彈性常數(shù)往往由于傾斜低估一個cos2α因素（這里α為相對水平傾斜角度，通常約12°）。如果沒有適當(dāng)?shù)男拚赡軙?dǎo)致在力的測量上的錯誤。研究發(fā)現(xiàn)，對于參考懸臂和熱調(diào)諧方法，無需進一步校正。維度法，附加質(zhì)量法和Sader方法，需要進一步校正，得到有效的彈性常數(shù)，校正公式為

4　探針彈性常數(shù)校正方法的選擇

綜上所述，以上所有的校正方法，都有各自模型特點。總結(jié)現(xiàn)已發(fā)表的彈性常數(shù)校正方法的優(yōu)缺點與不確定度如表1所示。對于相對剛性的（即K＞1N/m）矩形懸臂，Sader方法更加適合，該方法的不確定度良好，測量方便。參考懸臂法也是不錯的選擇，但它操作不夠友好，對探針的損耗大，通常會帶來更多的不確定性。相對柔軟的懸臂（即K＜1N/m），熱調(diào)諧法則更適合也很簡便，不確定性相對較低。而對于柔軟的V形懸臂，Sader方法則不適用，參考懸臂法則是不錯的選擇。

表1　已發(fā)表的彈性常數(shù)校正方法的優(yōu)缺點與不確定性的概述

結(jié)合筆者所在實驗室目前使用較多的探針類型和測試儀器型號（Bruker Multimode 8），在考慮已知懸臂參數(shù)的情況下，可采用的方法如表2所示。當(dāng)然，在進行彈性常數(shù)校正實驗的實際操作中，不僅要考慮探針懸臂本身的實際情況（形狀、尺寸、已知參數(shù)等條件），還要考慮每種方法執(zhí)行的難易程度；同時，選用的方法其誤差大小是否在可以接受的范圍也需要事先考慮清楚；當(dāng)然，實驗人員對哪種方法運用更熟練也是非常重要的因素。

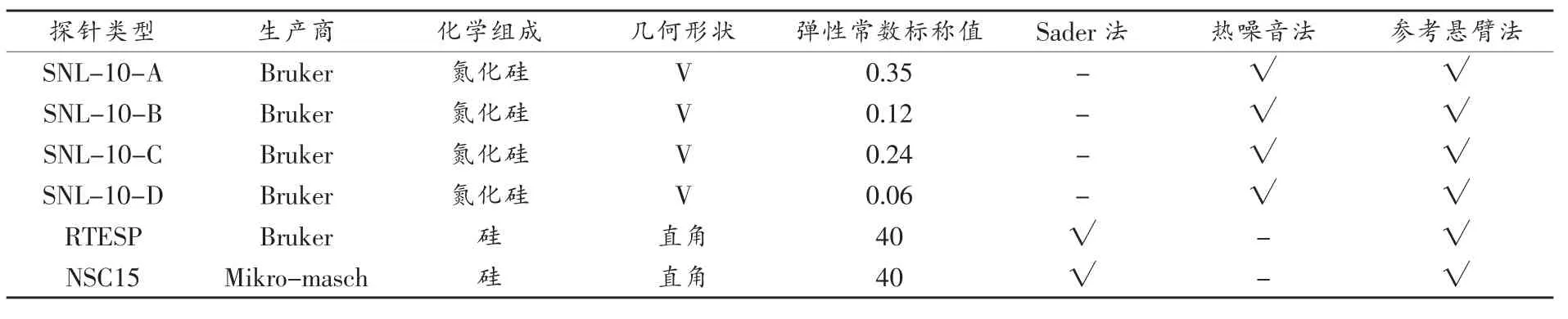
表2　不同類型探針彈性常數(shù)校正方法的選擇

5　結(jié)束語

通過借助一些額外的設(shè)備，如電子或光學(xué)顯微鏡等，原子力顯微鏡探針懸臂的彈性常數(shù)獲得了更為準確的表征。隨著這些輔助測量儀器的精密度的提高，彈性常數(shù)校正方法的準確程度也必將不斷提高。對于今后彈性常數(shù)校正的研究，不僅需要對校正方法準確度的提高進行研究，還應(yīng)該對校正方法進行不斷的簡化[20-21]，追求更加精確、先進的校正方法。

[1]RAMAN A，TRIGUEROS S，CARTAGENA A，et al. Mapping nanomechanical properties of live cells using multi-harmonic atomic force microscopy[J].Nature Nanotechnology，2011（6）：809-814.

[2]STAN G，SOLARES S D，PITTENGER B，et al.Nanoscale mechanicsbytomographiccontactresonanceatomic force microscopy[J].Nanoscale，2014（6）：962-969.

[3]GEORGAKAKID，MITRIDIS S，Sapalidis A A，et al. Calibration of tapping AFM cantilevers and uncertainty estimation：Comparisonbetweendifferentmethods[J]. Measurement，2013（46）：4274-4281.

[4]CLEVELAND J P，MANNE S，BOCEK D，et al.A nondestructive method for determining the spring constant of cantilevers for scanning force microscopy[J].Rev Sci Instrum，1993（64）：403-405.

[5]BUTT H，SIEDLE P，SEIFERT K，et al.Scan speed limit in atomic force microscopy[J].J Micro，1992（169）：75-84.

[6]ALBRECHT T R，AKAMINE S，CARVER T E，et al. Microfabrication of cantilever styli for the Atomic Force Microscope[J].J Vac Sci Tech，1990（8）：3386-3396.

[7]SADER J E.Parallel beam approximation for V-shaped atomic force microscope cantilevers[J].Rev Sci Instrum，1995（66）：4583-4587.

[8]WARMACK R，ZHENG X Y，THUNDAT T，et al. Friction Effects in the Deflection of Atomic Force Microscope Cantilevers[J].Rev Sci Instrum，1994（65）：394-399.

[9]TORTONESE M.Cantilevers and tips for atomic force microscopy[J].IEEE Eng Med Bio，1997（16）：28-33.

[10]CHOI J L，GETHIN D T.Simulation of atomic force microscopy operation via three-dimensional finite element modelling[J].Nanotechnology，2009（20）：1-14.

[11]GIBSON C T，WATSON G S，MYHRA S.Determination of the spring constants of probes for force microscopy/ spectroscopy[J].Nanotechnology，1996（7）：259-262.

[12]GATES R S，REITSMA MARK G.Precise atomic force microscope cantilever spring constant calibration using a reference cantilever array[J].Rev Sci Instrum，2007（78）：086101-3.

[13]CLIFFORD C A，SEAH M P.Improved methods and uncertainty analysis in the calibration of the spring constant of an atomic force microscope cantilever using static experimental methods[J].Meas Sci Technol，2009（20）：125501-10.

[14]KIM M S，CHIO J H，KIM J H，et al.Accurate determination of spring constant of atomic force microscope cantilevers andcomparison with other methods[J].Measurement，2010（43）：520-526.

[15]SLATTERY A D，BLANCH A J，QUINTON J S，et al. Calibration of atomic force microscope cantilevers using standard and inverted static methods assisted by FIB-milled spatial markers[J].Nanotechnology，2013（24）：015710-13.

[16]GREEN C P，LIOE H，CLEVELAND J P，et al.Normal andtorsionalspringconstantsofatomicforce microscope cantilevers[J].Rev Sci Instrum.，2004（75）：1988-1995.

[17]SADER J E，CHON J W M，MULVANDY P.Calibration of rectangular atomic force micro scope cantilevers[J]. Rev Sci Instrum，1999（70）：3767-3969.

[18]PIRZER T，HUGEL T.Atomic force microscopy spring constant determination in viscous liquids[J].Rev Sci Instrum，2009（80）：035110-6.

[19]SADER J E，SANELLI J A，ADAMSON B D，et al. Spring constant calibration of atomic force microscope cantilevers of arbitrary shape[J].Rev Sci Instrum，2012（83）：103705-16.

[20]SADER J E，F(xiàn)RIEND J R.Calibration of atomic force microscopecantileversusingonlytheirresonant frequency and quality factor[J].Review of Scientific Instruments，2014（85）：116101-3.

[21]SLATTERY A D，BLANCH A J，EJOV V.Spring constant calibration techniques for next-generation fastscanningatomicforcemicroscopecantilevers[J]. Nanotechnology，2014（25）：335705-13.

[22]SADER J E，LU J，MULVANEY P.Effect of cantilever geometry on the optical lever sensitivities and thermal noise method of the atomic force microscope[J].Rev Sci Instrum，2014（85）：113702-6.

[23]PROKSCH R，SCHAFFER T E，CLEVELAND J P，et al. Finiteopticalspotsizeandpositioncorrectionsin thermal spring constant calibration[J].Nanotechnology，2004（15）：1344-1350.

[24]SCHAFFER T E.Calculation of thermal noise in an atomic forcemicroscopewithafiniteopticalspotsize[J]. Nanotechnology，2005（16）：664-670.

（編輯：徐柳）

Research progress on the calibration methods for elastic constant of atomic force microscopy cantilevers

QU Zehua，BU Juan，PAN Xiaoxia
（State Key Laboratory of Molecular Engineering of Polymers，Department of Macromolecular Science，F(xiàn)udan University，Shanghai 200433，China）

It’s vital to know exactly the elastic constant of the cantilever of an atomic force microscope before the mechanical properties of material surfaces are quantitatively characterized with this device.This paper has reviewed corresponding calibration methods used in recent years，comprising dimensional method，static deflection and dynamic deflection.The dimensional method is designed for expounding different cantilever shapes（mostly rectangular and V-shaped），the mathematical models and their advantages and disadvantages of different methods will be analyzed in this paper.The static deflection is used to explain the mathematical models and the study on the accuracy improvement of these methods particularly.The dynamic deflection is reviewed separately with three approaches namely added mass method，Sader method and thermal tuning method.The model characteristics and advancement of the three methods are compared here.In the end，several suitable calibrations also be discussed for common cantilevers;the research prospect of these calibration methods are proposed.

cantilever；elastic constant；calibration；summary

A

1674-5124（2016）03-0001-06

10.11857/j.issn.1674-5124.2016.03.001

2015-09-18；

2015-11-19

聚合物分子工程國家重點實驗室儀器類開放課題（KVH1717101/001/018）

屈澤華（1978-），女，吉林九臺市人，博士，主要從事原子力顯微鏡、掃描電鏡相關(guān)研究工作。