基于CS的無線傳感器網絡動態分簇數據收集算法

張　策　張　霞　李　鷗　王　沖　張大龍

(中國人民解放軍信息工程大學信息系統工程學院　鄭州　450001)

?

基于CS的無線傳感器網絡動態分簇數據收集算法

張策張霞李鷗王沖張大龍

(中國人民解放軍信息工程大學信息系統工程學院鄭州450001)

(cezhang@foxmail.com)

降低能耗、實現網絡的能量均衡和延長網絡壽命，是設計無線傳感器網絡(wireless sensor networks, WSNs)數據收集算法所面臨的主要挑戰之一.針對現有無線傳感器網絡分簇數據收集算法不考慮網絡中事件源的發生對數據空間相關性的影響的情況，提出了一種基于壓縮感知的以事件源為中心的動態分簇(CS-based dynamic clustering centred on event source, CS-DCES)算法.該算法利用歐氏距離空間相關性模型和第一聯合稀疏模型，將受同一個事件源影響的節點分在一個簇中，并以簇為單位進行數據重構，以此增加簇內節點感知數據的空間相關性，減小每簇數據觀測量；利用壓縮感知收集數據，計算事件源位置，根據事件源位置變化實行動態分簇.并通過實驗分析了影響該算法性能的3個因素，即事件的衰減系數、事件源之間的距離和事件源個數，最后給出了算法的適用條件.仿真分析表明，相對于已有算法，CS-DCES在滿足同一重構精度的前提下，有效減小了數據傳輸量，節省網絡能耗，延長網絡壽命.

無線傳感器網絡；數據收集；事件源；空間相關性；動態分簇

無線傳感器網絡(wireless sensor networks, WSNs)廣泛應用于醫療救護空間探索、軍事應用、智能家居和環境監測等領域，被看作連接人類社會與物理世界的紐帶.傳感器節點通常依靠電池供電，能量受限，因此降低能耗、延長網絡壽命是WSNs數據收集方法研究的一大挑戰.

WSNs中節點布設密度大，節點感知到的數據存在大量冗余信息，且受環境影響十分大.傳統的數據收集方法是通過多跳中繼的方式將節點采集到的信息傳送給匯聚節點(Sink)，這種方法會收集到大量冗余信息，且越靠近Sink的節點需要轉發消息的次數越多、耗能越快，在Sink周圍易形成能量空洞，使整個網絡癱瘓.

近年來，壓縮感知理論(compression sensing, CS)[1-3]給信息處理領域帶來了革命性的突破，它指出將可壓縮高維信號投影到某個特定低維空間上，通過數值最優化問題從這些少量投影中準確重構出原始信號.文獻[4]將CS理論應用在單跳的WSNs，實現了對數據的壓縮;文獻[5-6]將壓縮感知理論應用于大規模多跳WSNs中，有效減少網內數據的傳輸能量損耗，且保持了網內能量均衡.壓縮感知理論在WSNs中數據收集的成功應用，解決了網絡能量消耗不均衡問題，且具有壓縮過程簡單而數據重構過程復雜的特點，適合傳感器節點信息處理能力不足和能源受限的特點.文獻[7]針對WSNs分布式數據收集特點，首次提出分布式壓縮感知理論(distributed compressed sensing, DCS)，實現了在WSNs中對多信號的壓縮感知編碼.文獻[8]將CS技術與Pegasis路由協議相結合，構建路由鏈，在鏈中壓縮數據以改善網絡壽命，在Sink處統一重構數據，與樹形路由中最小生成樹相比，雖然鏈路路由中節點之間每一跳能耗最小，但整個鏈路能耗不一定達到最小，且網絡魯棒性差.文獻[5,9]將CS技術與樹形路由協議相結合，以獲得高效的壓縮數據，但是簡單地在樹形路由中使用CS，會增加葉節點和距離葉節點較近的中間節點的通信量，而網絡的吞吐量并沒有提升.文獻[10]針對該問題提出了混合壓縮感知(Hybrid-CS)數據收集方法，在樹形路由中僅僅對一部分通信量高的父節點使用壓縮感知技術，以此減少網絡數據通信量.

以上研究針對平面網絡結構，當網絡規模較大時，通過分簇構建層次化網絡結構，更有助于提高網絡數據傳輸和管理的效率.文獻[11]借鑒Leach的思想，研究適合于分簇結構的壓縮感知數據收集，建立模型計算出全網最優簇首個數，隨機選取簇首，并使得簇首均勻分布在網絡中，Sink得到每個簇收集到的數據后統一重構.以上文獻均沒考慮節點感知數據之間的相關性問題和事件源對數據相關性的影響，在WSNs中會有一些人們感興趣的事件源發生，如溫度監測場景中的著火點，影響著局部采集數據之間的空間相關性.文獻[12-15]分析了WSNs網絡性能受空間相關性的影響很大.文獻[16]分析了網絡中影響源對數據相關性的影響，簇內的全局影響因子會使得簇中的共有稀疏度增加而特有稀疏度減小，總的稀疏度和觀測數量M減小，通過空間相關性和最優距離對網內節點分簇，在Sink端統一重構，但是文中沒有確切地給出影響源的位置和影響范圍.

為此本文提出一種基于壓縮感知的以事件源為中心的動態分簇(compressive sensing based dynamic clustering centered on event source, CS-DCES)算法，考慮網絡中事件源的發生對數據相關性的影響，以事件源為中心進行分簇，每個簇內收集到的數據單獨進行數據重構;在數據收集過程中計算事件源方位，根據事件源方位變化動態分簇，以實現高精度、低能耗的數據收集.

1　系統模型

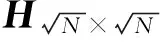
(1)

(2)

WSNs中，每個傳感器節點采集的信號強度是由網絡中S個事件源的信號疊加而成的，即[17]

XN×1=ΨN×NVN×1=

(3)

其中Ψ為傳感器感知數據隨距離衰減系數矩陣.本文利用歐氏距離的空間相關性模型.假定傳感器節點i和j的坐標為(xi,yi)和(xj,yj)，2節點之間的距離為

(4)

若在節點i處有事件源發生，節點i接收到信號功率為Pi，節點j接收到信號功率為Pj，信號按歐氏距離衰減，則有

(5)

其中,C為常數，n為信號的衰減系數.不同類型的事件源衰減系數不同.2個區域中節點采集到的信息之間的相關性與其歐氏距離成反比，距離越近、衰減系數n越小，節點采集到的信息越接近，相關性越大.本文令：

(6)

使用壓縮感知技術進行數據收集，假設隨機觀測矩陣為Φ=(φi j)M×N，其中M?N，使用文獻[7]中給出的測量矩陣：

(8)

一般地，由于網絡中事件源發生個數S?N，向量V是稀疏的.通過此模型，可以將計算事件源方位向量V問題轉化為已知Y求V的問題.根據文獻[17]，式(8)符合壓縮感知理論的觀測模型，可將計算過程轉化為一個求解凸優化問題：

(9)

2　基于相關性模型的分簇方法

在大規模WSNs中，節點感知到的數據之間存在著空間上的相關性.本文利用第一聯合稀疏模型(joint sparsity model-1, JSM-1)[18]對WSNs中節點采集到的信息進行建模分析.

在JSM-1中，假設網絡中有N0個節點，節點j采集數據xj可以分為共有數據部分zc和特有數據部分zj，即：

(10)

共有數據與特有數據在同一個稀疏基Ψ下稀疏表示為：

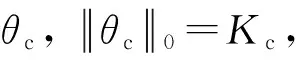
(11)

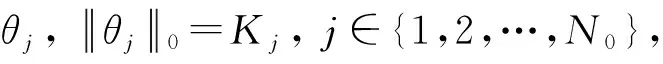
(12)

其中,共有數據的稀疏度為Kc，特有數據zj的稀疏度為Kj.根據壓縮感知理論要求，為了保證在數據重構時的精度，觀測次數M滿足：

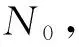
(13)

(14)

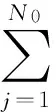
傳統的壓縮感知數據收集方法中，將所有傳感器節點采集的信息統一進行重構.然而由于網絡環境復雜，往往有多個分布于不同區域的事件，影響傳感器節點采集的數據，這些事件之間是彼此獨立的.例如，在室外溫度測量場景，全局影響因子如日照、風等，影響共有數據部分zc；局部影響因子如水流、動物和著火點等，影響特有數據部分zj.在這種情況下，全網節點統一進行處理的將使得Kc較小而Kj較大，總的稀疏度K增大，從而使得觀測次數M增高.

網絡中的事件源會成為影響其周邊節點感知數據的主要因素，且節點離事件源越近，受影響程度將越大.因此本文提出以事件源為中心分簇.假設簇內共有N1個節點，若隨機分簇，以簇為單位進行數據重構，則簇內總稀疏度Kintra為：

(15)

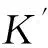
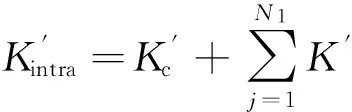
(16)

3　動態分簇數據收集算法

針對有感興趣的事件源發生的WSNs，本文根據以上2種模型，提出了基于壓縮感知的動態分簇數據收集算法.整個算法流程如圖1所示：

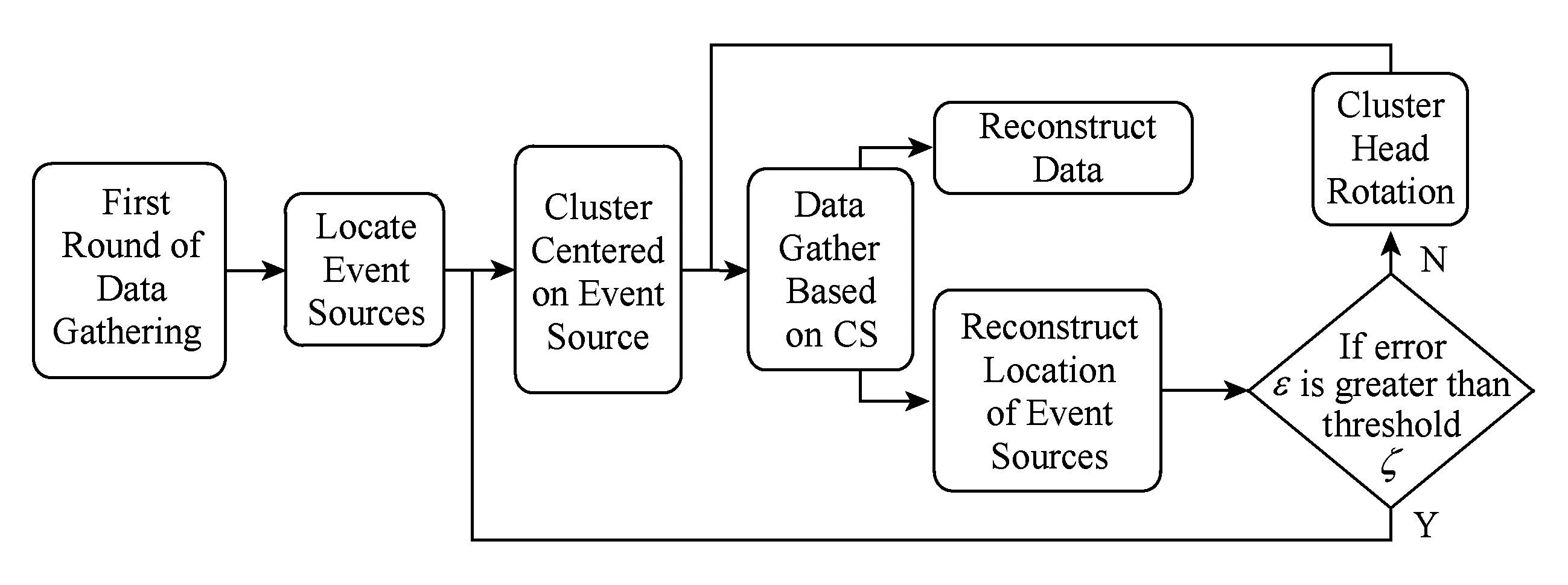
Fig. 1　CS-DCES algorithm flow chart.圖1　CS-DCES算法流程圖

算法具體過程如下：

1) 獲取事件源方位.假設網絡中有事件源發生，且Sink已經得到了全網節點采集到的數據Xtot，此數據可以通過非壓縮感知算法或者壓縮感知算法方式獲得.由系統模型中式(3)可知，事件源方位向量Vtot為

(17)

2) 以事件源為中心分簇.根據相關性模型，Sink獲取事件源方位后，通知距離每個事件源位置最近的傳感器節點，將其確定為簇首；若同時有多個節點與事件源距離相等且最近，則Sink在這些節點中隨機選出1個節點作為本簇簇首，此時一定會選出1個簇首，即分簇收斂.由簇首廣播其簇首信息，其余節點選擇距離自己最近的簇首，加入該簇.Sink為每個簇首分配不同的隨機種子ξ，簇首接收隨機種子ξ后與本簇內成員節點IDj組合生成隨機種子(ξ,IDj)，利用該種子隨機生成M維的觀測矩陣Φ′.圖2為網絡中有3個事件源時的分簇情況.

Fig. 2　Network clustering diagram.圖2　網絡分簇示意圖

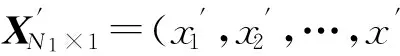
算法1. 在有N1個成員節點的簇中，簇首在第t輪第i個測量值的收集算法.

②fori=1toM

④ end for

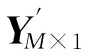
⑥ end if

4) 數據重構.Sink收到S個簇首發送的觀測向

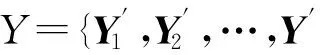
算法2. Sink重構第i個簇內的數據.

① if Sink 收到簇首觀測向量Yithen

②fori=1toS

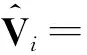
ΦiΨiVi;

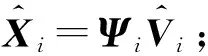
⑤ end for

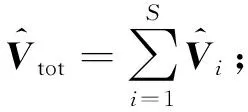
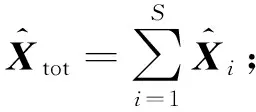
⑧ end if

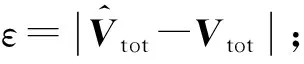
⑩ ifε>ζthen

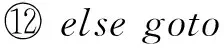
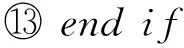
6) 簇首輪換.若經Sink判斷，網絡中事件源方位沒有發生變化，為了使簇中能耗均衡，1次數據收集后，保持各個簇的規模和位置不變，在簇內實行簇首輪換.各個簇內的成員節點將自身剩余能量信息發送至簇首，由簇首判斷選取簇內剩余能量最大的節點作為下一輪數據收集的簇首，并將新簇首信息發送給簇內其余成員節點進行簇首輪換，以防止簇內能量消耗不均衡造成網絡過早癱瘓.

4　仿真與分析

為了驗證CS-DCES算法的有效性，本文在MATLAB平臺下進行算法仿真分析，仿真環境設置如下：全網有400個傳感器節點均勻分布在20×20的區域中，網絡中有S個事件源發生.Sink在網絡中的坐標為(10,50)并有固定的能源供應，假設網絡中普通節點的初始能量值為0.05，一旦其能量小于0時，即認為該節點死亡停止工作，本文采用正交匹配追蹤算法(orthogonalmatchingpursuit,OMP)作為重構算法.

在WSNs中，大部分基于壓縮感知的數據收集算法較少考慮采集數據由于受不同事件源影響導致空間相關性改變，而把網絡中所有節點采集的數據看作1個信號并在Sink處統一重構，例如文獻[11],為了便于描述，本文將該類算法記為CS-URA(unifiedrestructuringalgorithm)算法.文獻[16]中的SC-CDG算法考慮了網絡中事件源對數據相關性的影響，卻沒有確切地給出影響源的位置和影響范圍，本文擬與CS-URA算法和SC-CDG算法進行比較，比較3種算法在重構數據信噪比和網絡壽命上的性能優劣.仿真結果為1 000次仿真之后的平均值.

整個網絡中的能量消耗，主要是節點與簇首、簇首與Sink之間的無線通信能耗.本文采用文獻[11]給出的能量消耗模型，即

ETx(L,d)=Eelec×L+εamp×L×d2,

ERx(L)=Eelec×L,

其中，ETx(L,d)表示數據發送節點將1個L位的數據傳輸d時所消耗的能量，ERx(L)表示數據接收節點接收L位數據消耗的能量，Eelec表示節點發送或接收單位位所消耗的能量，εamp表示節點功率放大系數.

4.1算法性能比較

如圖3所示給出了重構信噪比SNR和觀測次數M的關系.仿真假設網絡中有2個事件源發生，其位置為(15,5)和(5,15)，衰減系數n=4.由圖3可知，隨著觀測次數M的增加，信噪比提高，且只需較小的觀測次數就能達到較高的重構精度；當M持續增大，信噪比趨于平穩，重構精度達到最優，M的持續增大并不會帶來更高的重構精度，反而會增加網絡的能耗開銷.當信噪比SNR=27 dB時，CS-URA算法觀測次數M=33，SC-CDG算法觀測次數M=32，而CS-DCES算法的觀測次數為M=13，減少了60%左右.由于CS-DCES算法以事件源為中心，將空間相關性高的節點分在一個簇中，與其他2種算法相比使得簇內總的稀疏度降低，當以簇為單位重構數據時，可以以較小的觀測次數M達到同樣的精度.

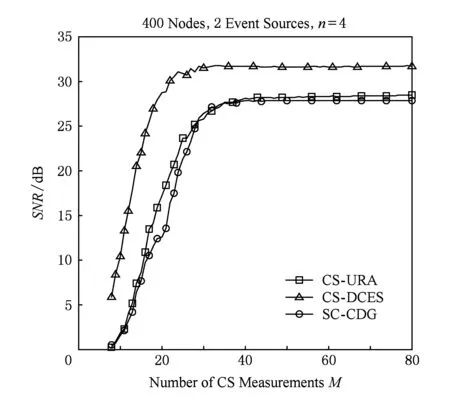
Fig. 3　The relationship between reconstruction SNR 　　　and the number of measurements.圖3　重構信噪比與觀測次數關系

圖4反映了當數據包長度為1 B、信噪比SNR=27 dB時數據收集輪數r與死亡節點數的關系圖.由仿真結果可得，CS-URA算法在收集445輪時第1個節點死亡，收集674輪時所有節點死亡；SC-CDG算法在收集632輪時第1個節點死亡，收集641輪時所有節點死亡；CS-DCES算法收集1892輪時第1個節點死亡，收集2 164輪時所有節點死亡.相比之下，網絡壽命增加了221%和237%，有效延長了網絡壽命，且由于本方法使用了簇首輪換機制，使得整個網內能耗得到了均衡.

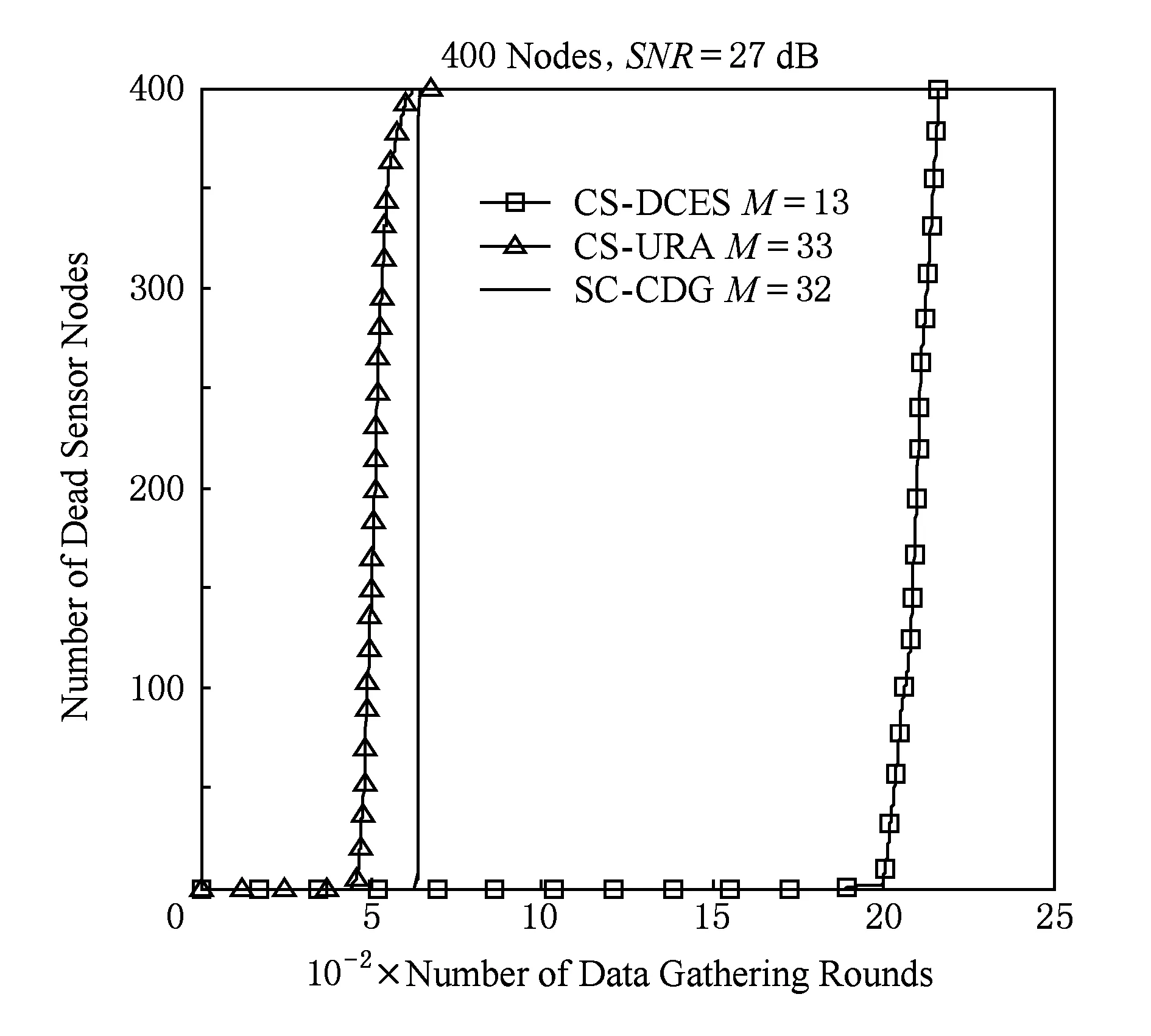
Fig. 4　Network lifetime.圖4　網絡壽命

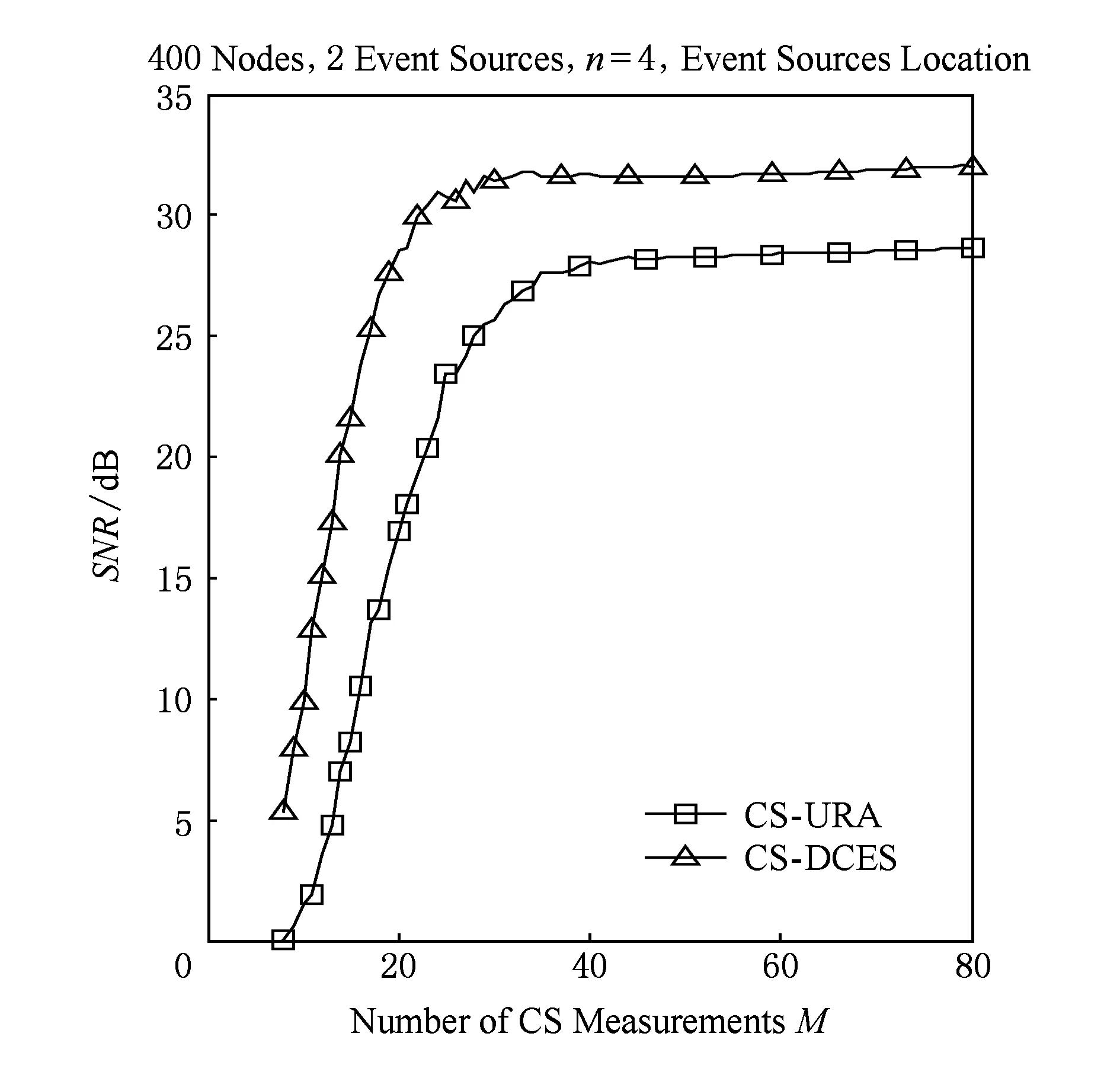
Fig. 5　Reconstruction of event source position.圖5　事件源位置重構

4.2定位事件源

在CS-DCES算法中，事件源位置的確定直接決定了算法的有效性.在本文所建立的模型下，CS-DCES與CS-URA均能重構出事件源位置，CS-DCES算法在相同重構精度時所需觀測次數更少，其性能如圖5所示.CS-DCES算法重構事件源方位如圖6所示.由圖6可知CS-DCES算法可以精確重構出事件源位置，以判斷事件源位置是否發生變化，為本算法的有效性提供了條件.

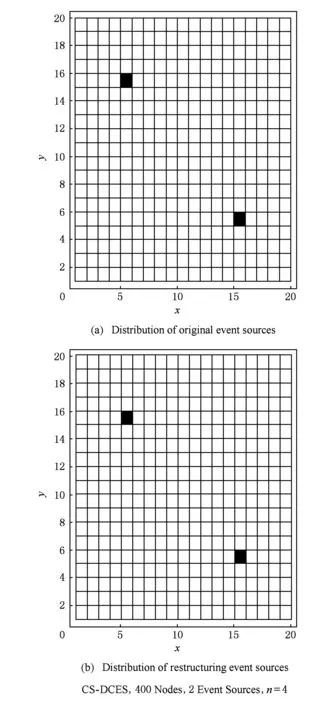
Fig. 6　Event source distribution map.圖6　事件源分布圖

4.3影響算法性能因素分析

CS-DCES算法是以事件源為中心對全網節點進行分簇，所以事件的衰減系數n、事件源之間的距離d和事件源個數S都會影響CS-DCES的性能，下面通過仿真討論上述因素對算法性能的影響.

圖7是衰減系數n與SNR的關系.2個事件源位置為(1,1)和(20,20)，相距d=26.87.當衰減系數分別為2.5，3，3.5，4，6，8時，較小的觀測次數M就能達到較高的SNR;當衰減系數n=2時，即事件源的影響范圍擴大，SNR最高只有15，重構精度變低，此時CS-DCES算法就不再適用.進一步仿真了n=2時CS-URA算法的性能，并與CS-DCES算法進行了對比，結果如圖8所示.

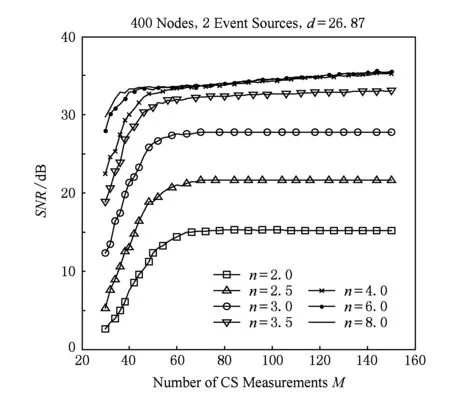
Fig. 7　Impact of attenuation coefficient on performance.圖7　衰減系數對性能影響

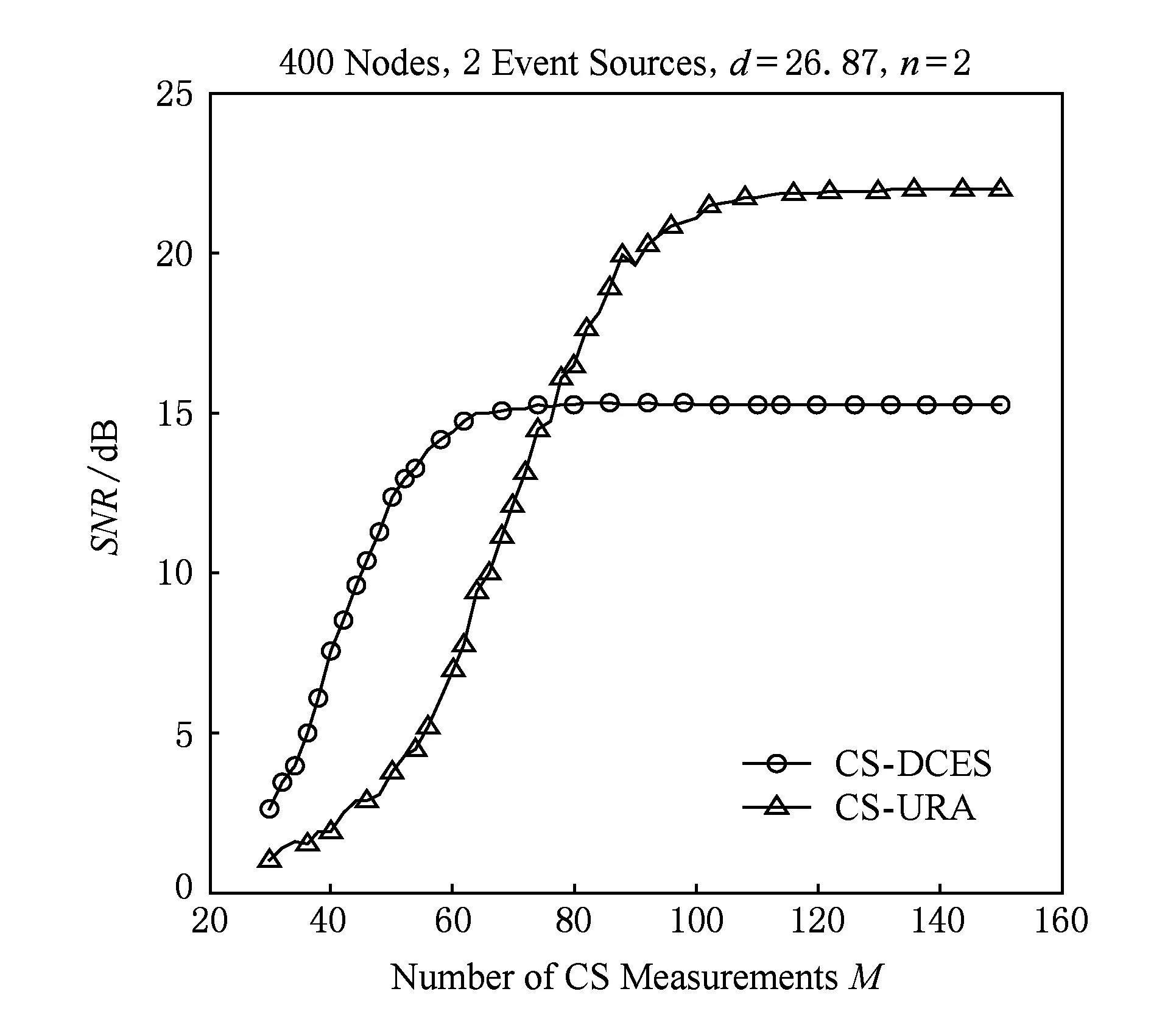
Fig. 8　Comparison of CS-DCES and CS-URA. 圖8　CS-DCES算法與CS-URA算法性能對比

M<76時,CS-URA算法的精度沒有CS-DCES算法的高；M>76時，CS-URA算法卻能達到較高精度.由于CS-DCES算法根據節點與事件源的距離，將主要受同一個事件源影響的節點分在一個簇中.當n減小，會使得位于2個事件源之間、同時受到這2個事件源影響的節點受影響的程度增大，且使2種影響程度差距變小.這樣在每個簇單獨重構時，簇中一部分節點采集到的數據主要受本簇中事件源的影響，另一部分節點采集到的數據同時受2個事件源的影響，此時CS-DCES算法中簇內總稀疏度K并不會減小甚至增大，重構誤差變大，性能變差.

圖9反映了網絡中有2個事件源時，事件源距離d對CS-DCES算法性能的影響.圓形曲線表示2個事件源位于(3,3)和(18,18)時算法性能，三角曲線表示2個事件源位于(7,5)，(13,19)時算法性能，方形曲線表示2個事件源位于(10,9)，(9,15)時算法性能.由圖9可知,事件源之間距離越大，SNR越高.當事件源之間的距離很小時，重構精度會很差，此時CS-DCES算法將不再具有優越性能.事件源距離的增大，削弱了簇與簇之間的相互影響，使得簇內的數據相關性主要受本簇內事件源的影響，從而降低簇中數據的稀疏度，減小觀測次數.

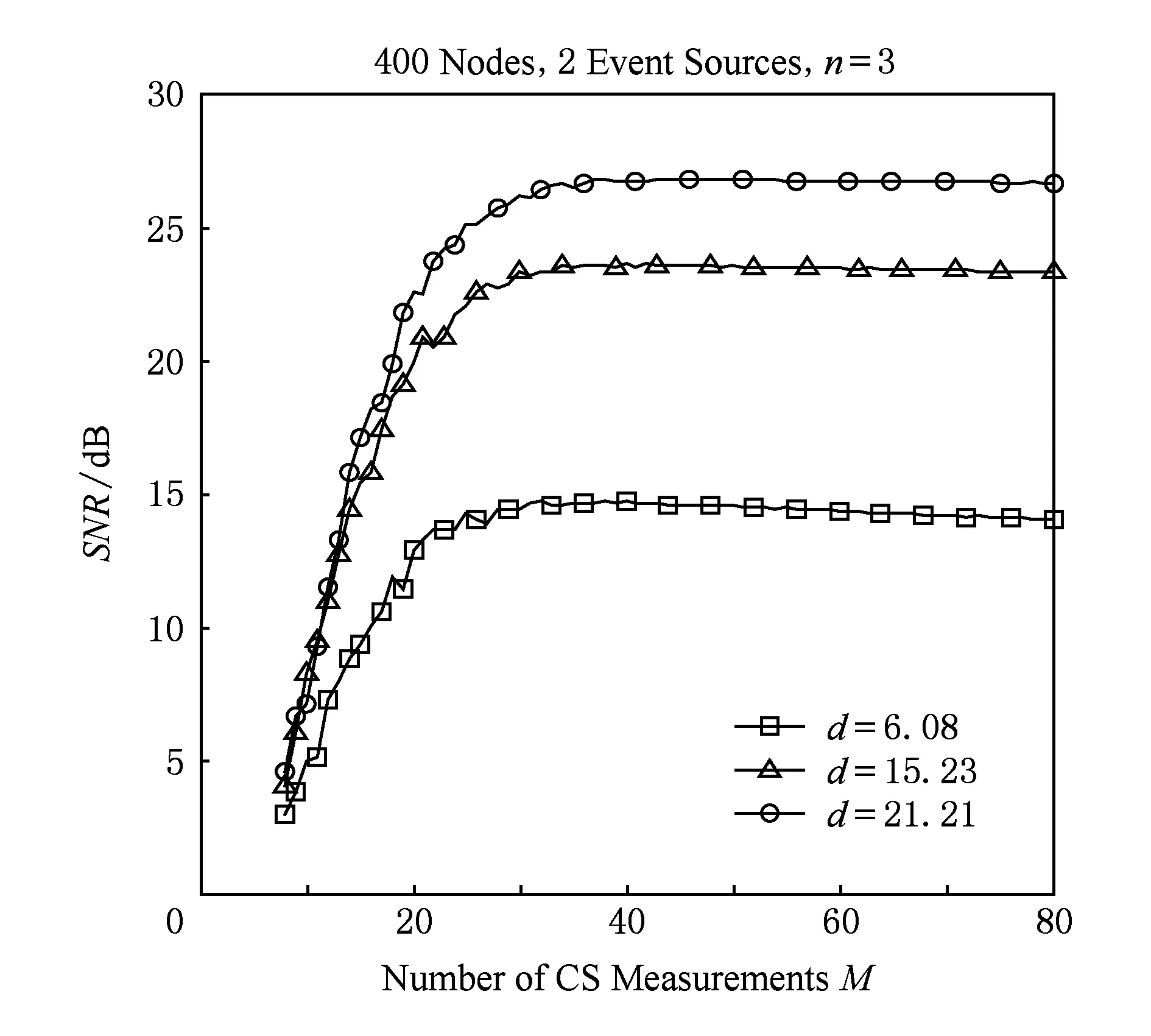
Fig. 9　Impact of event source distance on performance.圖9　事件源距離對性能影響

圖10為事件源個數S對CS-DCES算法性能的影響.衰減系數n=4，使得事件源均勻地分布在網絡中，正方形曲線表示事件源位于(5,15)，(15,5)時的算法性能，三角形曲線表示事件源位于(3,3)，(18,18)，(15，9)時的算法性能，圓形曲線表示事件源位于(5,5)，(5,15)，(15,5)，(15,15)時的算法性能.由仿真圖可知，事件源個數越少且相距越遠時，CS-DCES算法的性能越好.事件源個數的增多使得事件源之間距離減小的概率增加，在衰減系數一定的情況下，簇與簇之間的影響有可能會增大，算法性能就會受到影響;若事件源個數增多但彼此之間相距較遠，則本算法性能同樣不會變差.

由以上仿真結果可以得出，當WSNs中事件源的衰減系數小、距離大、個數少時，CS-DCES算法能保證收集數據重構精度的同時減少數據收集的能耗，延長網絡壽命，性能優勢明顯.

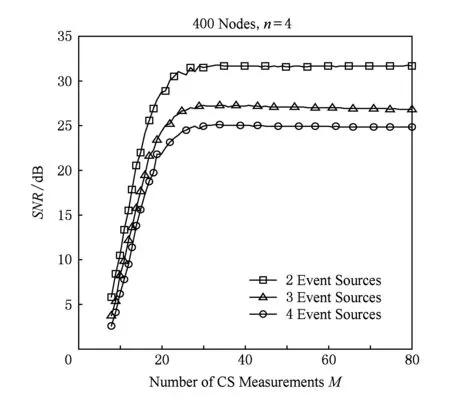
Fig. 10　Impact of number of event sources on performance.圖10　事件源個數對性能影響

5　總結和展望

本文針對有事件源發生的WSNs數據收集提出了CS-DCES算法，以此來增加簇內數據相關性，使得數據共有稀疏度增加而特有稀疏度減小，總的稀疏度減小，減小簇內觀測次數.并根據事件源的位置變化調整分簇策略，實現動態分簇.通過仿真實驗分析了算法性能，結果表明，本算法在同一重構精度前提下有效減小了數據傳輸量、節省網絡能耗、延長網絡壽命;討論了衰減系數、事件源距離和事件源個數對算法性能的影響，算法在衰減系數大、事件源相距遠和事件源個數少時，CS-DCES算法的重構精度更高、網絡壽命更長，更具有優勢.

在實際WSNs應用場景中均勻規則布設節點一般很難實現，且網絡鏈路并非完全可靠.為了能將此模型算法運用到實際的工程中去，對隨機布設節點的系統模型和算法實現的研究很有必要，WSNs在不可靠鏈路條件下運用壓縮感知技術也將在后續研究工作中進行討論.

[1]Donoho D L. Compressed sensing [J]. IEEE Trans on Information Theory, 2006, 52(4): 1289-1306[2]Baraniuk R. Compressive sensing [J]. IEEE Signal Processing Magazine, 2007, 56(4): 4-5[3]Candes E J, Wakin M B. An introduction to compressive sampling [J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30[4]Rabbat M, Haupt J, Singh A, et al. Decentralized compression and predistribution via randomized gossiping [C]Proc of the 5th Int Conf on Information Processing in Sensor Networks. New York: ACM, 2006: 51-59[5]Luo C, Wu F, Sun J, et al. Compressive data gathering for large-scale wireless sensor networks [C]Proc of the 15th Annual Int Conf on Mobile Computing and Networking. New York: ACM, 2009: 145-156[6]Wang J, Tang S, Yin B, et al. Data gathering in wireless sensor networks through intelligent compressive sensing [C]Proc of IEEE INFOCOM 2012. Piscataway, NJ: IEEE, 2012: 603-611[7]Wang W, Garofalakis M, Ramchandran K. Distributed sparse random projections for refinable approximation. [C]Proc of the 6th Int Conf on Information Processing in Sensor Networks. New York: ACM, 2007: 331-339[8]Osamy W, Salim A, Aziz A. Efficient compressive sensing based technique for routing in wireless sensor networks [J]. INFOCOMP Journal of Computer Science, 2013, 12(1): 1-9[9]Luo C, Wu F, Sun J, et al. Efficient measurement generation and pervasive sparsity for compressive data gathering [J]. IEEE Trans on Wireless Communications, 2010, 9(12): 3728-3738[10]Luo J, Xiang L, Rosenberg C. Does compressed sensing improve the throughput of wireless sensor networks? [C]Proc of IEEE Int Conf on Communications (ICC 2010). New York: IEEE Communications Society, 2010: 1-6[11]Wu X, Xiong Y, Huang W, et al. An efficient compressive data gathering routing scheme for large-scale wireless sensor networks [J]. Computers & Electrical Engineering, 2013, 39(6): 1935-1946[12]Pattem S, Krishnamachari B, Govindan R. The impact of spatial correlation on routing with compression in wireless sensor networks [J]. ACM Trans on Sensor Networks, 2008, 4(4): 24-31[13]Villas L A, Boukerche A, Oliveira H A B F D, et al. A spatial correlation aware algorithm to perform efficient data collection in wireless sensor networks [J]. Ad Hoc Networks, 2014, 12(1): 69-85[14]Gupta G, Misra M, Garg K. Energy efficient data gathering using prediction-based filtering in wireless sensor networks [J]. International Journal of Information and Communication Technology, 2013, 5(1): 75-94[15]Villas L A, Boukerche A, Guidoni D L, et al. An energy-aware spatio-temporal correlation mechanism to perform efficient data collection in wireless sensor networks [J]. Computer Communications, 2013, 36(9): 1054-1066

[16]Wang Chong. Research on data gathering based on compressive sensing in wireless sensor networks [D]. Zhengzhou: PLA Information Engineering University, 2015: 37-44 (in Chinese)(王沖. 基于壓縮感知的無線傳感網數據收集技術研究[D]. 鄭州: 中國人民解放軍信息工程大學, 2015: 37-44)[17]Tang Liang, Zhou Zheng, Shi Lei, et al. Source detection in wireless sensor network by LEACH and compressive sensing [J]. Journal of Beijing University of Posts & Telecommunications, 2011, 34(3): 8-11 (in Chinese)(唐亮, 周正, 石磊, 等. 基于LEACH和壓縮感知的無線傳感網目標探測 [J]. 北京郵電大學學報, 2011, 34(3): 8-11)[18]Duarte M F, Sarvotham S, Wakin M B, et al. Joint sparsity models for distributed compressed sensing[C]Proc of the Workshop on Signal Processing with Adaptative Sparse Structured Representations. Piscataway, NJ: IEEE, 2005: 2729-2732

Zhang Ce, born in 1991. Master candidate. His main research interests include wireless sensor networks, routing protocol, and communication technology.

Zhang Xia, born in 1979. PhD and lecturer. Her main research interests include computer network, wireless sensor networks, and information operations (zhangxiaatzz@sina.com).

Li Ou, born in 1961. Professor and PhD supervisor. His main research interests include wireless sensor networks, cognitive radio networks, and Ad-hoc networks (zzliou@126.com).

Wang Chong, born in 1989. Master candidate. His main research interests include wireless sensor networks, routing protocol, and communication technology (wc38022122@126.com).

Zhang Dalong, born in 1976. PhD and lecturer. His main research interests include wireless sensor networks, MAC protocol, and communication technology (ttengzhang@163.com).

Data Gathering Using Dynamic Clustering Based on WSNs Compressive Sensing Algorithm

Zhang Ce, Zhang Xia, Li Ou, Wang Chong, and Zhang Dalong

(SchoolofInformationSystemsEngineering,PLAInformationEngineeringUniversity,Zhengzhou450001)

One of the major challenges of designing wireless sensor networks data gathering algorithm is to reduce energy consumption, achieve better balanced consumption and prolong the lifetime of sensor network. For the current clustering algorithms of data gathering in wireless sensor networks neglecting the impact of event sources on data spatial correlation, a CS-based dynamic clustering algorithm centred on event source (CS-DCES) is proposed in this paper. Utilizing the model of Euclidean distance spatial correlation and joint sparsity model-1, the nodes that affected by the same event source are clustered together and reconstruct those nodes readings within cluster in order to increase the spatial correlation of data and reduce the number of each cluster measurement. The algorithm exploits the compressive data to calculate the location of event source and clusters dynamically. Moreover, according to simulation, we analyze the three factors that influence the algorithm performance, and they are attenuation coefficient of event sources, distance between event sources and the number of event sources, and finally the application condition of CS-DCES is given. The simulations show that CS-DCES outperforms the existing data gathering algorithms in decreasing communication cost, saving the network energy consumption and extending the network survival time under the same accuracy.

wireless sensor networks(WSNs); data gather; event source; spatial correlation; dynamic clustering

2015-06-09；

2015-09-16

國家科技重大專項基金項目(2014zx03006003)

TP393

This work was supported by National Science and Technology Major Projects (2014zx03006003).