基于聚類算法的社團(tuán)發(fā)現(xiàn)算法研究

深圳壓寨網(wǎng)絡(luò)有限公司 王唐云

基于聚類算法的社團(tuán)發(fā)現(xiàn)算法研究

深圳壓寨網(wǎng)絡(luò)有限公司 王唐云

互聯(lián)網(wǎng)、云計算、大數(shù)據(jù)技術(shù)的快速發(fā)展，使人類社會加速進(jìn)入信息化時代。復(fù)雜網(wǎng)絡(luò)是信息發(fā)展的產(chǎn)物之一，其可以描述人類社會的各種系統(tǒng)，比如電力網(wǎng)絡(luò)、通信網(wǎng)絡(luò)、社交網(wǎng)絡(luò)等，利用復(fù)雜網(wǎng)絡(luò)可以幫助人們分享智慧信息帶帶來的便捷性，比如Twitter、Facebook、微信、QQ、微博等社團(tuán)應(yīng)用工具促進(jìn)人類社交，滿足人們多樣化、興趣化、智能化交友需求。社團(tuán)發(fā)現(xiàn)作為復(fù)雜網(wǎng)絡(luò)處理的重要手段，其可以提高信息利用精準(zhǔn)性。經(jīng)過多年研究和發(fā)展，社團(tuán)發(fā)現(xiàn)引入了先進(jìn)的聚類技術(shù)，采用譜聚類、K均值、信息論等多種聚類算法，更好的從復(fù)雜網(wǎng)絡(luò)搜尋人們期望的模型和信息，具有重要的作用和意義。

聚類算法；社團(tuán)發(fā)現(xiàn)；譜聚類；K均值；信息論

1.引言

復(fù)雜網(wǎng)絡(luò)是社會交際、電力工業(yè)、基因組織等復(fù)雜系統(tǒng)的一個具體表現(xiàn)形式，復(fù)雜網(wǎng)絡(luò)中的節(jié)點可以描述復(fù)雜系統(tǒng)中的實體，節(jié)點之間的邊可以描述實體之間的關(guān)系［1］。復(fù)雜網(wǎng)絡(luò)可以描述現(xiàn)實世界中的許多系統(tǒng)，比如生物系統(tǒng)中的蛋白質(zhì)交互網(wǎng)絡(luò)、神經(jīng)元網(wǎng)絡(luò)、基因調(diào)控網(wǎng)絡(luò)，社會系統(tǒng)中的人際關(guān)系網(wǎng)絡(luò)、流行病傳播網(wǎng)絡(luò)、科學(xué)家合作網(wǎng)絡(luò)，計算機(jī)系統(tǒng)中的萬維網(wǎng)、電子商務(wù)網(wǎng)、朋友圈網(wǎng)，電力系統(tǒng)中的電力通信網(wǎng)絡(luò)等，復(fù)雜網(wǎng)絡(luò)研究涉及多個學(xué)科，包括社會學(xué)、計算機(jī)學(xué)、心理學(xué)、統(tǒng)計學(xué)、圖形學(xué)、生物學(xué)等，隨著對復(fù)雜網(wǎng)絡(luò)的進(jìn)一步研究，在小世界現(xiàn)象和無標(biāo)度性之后，人們發(fā)現(xiàn)復(fù)雜網(wǎng)絡(luò)存在另外一個特性，就是其拓?fù)浣Y(jié)構(gòu)呈現(xiàn)出社團(tuán)結(jié)構(gòu)，也即是復(fù)雜網(wǎng)絡(luò)社團(tuán)之間的聯(lián)系是相對稀疏的，社團(tuán)內(nèi)部的連接相對稠密［2］。社團(tuán)發(fā)現(xiàn)可以積極的利用算法尋找復(fù)雜網(wǎng)絡(luò)中的社團(tuán)結(jié)構(gòu)，這樣就可以研究整個網(wǎng)絡(luò)的功能，更好的組織復(fù)雜系統(tǒng)，具有十分重要的意義。

2.社團(tuán)發(fā)現(xiàn)及其應(yīng)用

復(fù)雜網(wǎng)絡(luò)中的社團(tuán)發(fā)現(xiàn)是指在一個網(wǎng)絡(luò)中，使用某種技術(shù)可以將聯(lián)系較為緊密的節(jié)點劃分為一個社團(tuán)中，也可以把聯(lián)系較少的節(jié)點劃分為不同的社團(tuán)中，也即是盡可能的保持社團(tuán)內(nèi)部節(jié)點結(jié)構(gòu)緊密和社團(tuán)之間的節(jié)點邏輯獨立。社團(tuán)發(fā)現(xiàn)可以準(zhǔn)確的揭示復(fù)雜網(wǎng)絡(luò)中節(jié)點的組織關(guān)系，比如具有共同的愛好和興趣，屬于一個工作種類，屬于同一個省市縣區(qū)域等；社團(tuán)發(fā)現(xiàn)也可以提高網(wǎng)絡(luò)的搜索性能，實現(xiàn)信息過濾、追蹤熱點話題、采集和分析網(wǎng)絡(luò)輿情；社團(tuán)發(fā)現(xiàn)也可以發(fā)現(xiàn)復(fù)雜網(wǎng)絡(luò)系統(tǒng)中相關(guān)的結(jié)構(gòu)單一等［3］。復(fù)雜網(wǎng)絡(luò)社團(tuán)結(jié)構(gòu)如圖1所示。

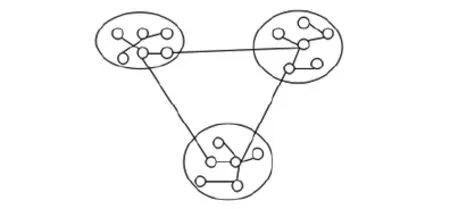
圖1 復(fù)雜網(wǎng)絡(luò)社團(tuán)結(jié)構(gòu)

社團(tuán)應(yīng)用領(lǐng)域非常多，最為常見的應(yīng)用就是社交網(wǎng)絡(luò)、基因組織、客戶關(guān)系管理等方面。比如，在電子商務(wù)領(lǐng)域，如果根據(jù)每一個客戶購買同類型商品的興趣進(jìn)行劃分和組織，可以很快的識別出這些客戶的群體，同時發(fā)現(xiàn)這些客戶歸屬的朋友圈，像這些客戶及其朋友推薦商品，可以更好的提高電商營銷的精準(zhǔn)程度，提高電商網(wǎng)站的成交率［4］。

3.基于聚類的社團(tuán)發(fā)現(xiàn)算法研究

3.1譜聚類算法

社團(tuán)網(wǎng)絡(luò)是一個圖結(jié)構(gòu)，譜聚類算法主要思想來源與譜圖劃分。假設(shè)G是一個擁有N個節(jié)點的復(fù)雜網(wǎng)絡(luò)，則G可以使用一個N×N的拉普拉斯矩陣L進(jìn)行描述，lii表示矩陣節(jié)點Vi的度，規(guī)定Vi與Vj連通，則lij=-1，否則lij=0，因此矩陣L與鄰接矩陣A的關(guān)系為L=K-A，矩陣K只能描述對角線節(jié)點對應(yīng)的連通度值，其余元素規(guī)定為0.由于矩陣L每一行或每一列元素之和均為0，則L存在一個零特征值和一個全為1的特征向量。如果G可以被劃分為M個費重疊社團(tuán)Gm，則這些社團(tuán)之間不存在連接，則網(wǎng)絡(luò)G的拉普拉斯矩陣可以劃分為M個對角矩陣，每一個對角矩陣表示一個社團(tuán)。

3.2K均值算法

K均值也是社團(tuán)發(fā)現(xiàn)常用的算法，其可以將復(fù)雜網(wǎng)絡(luò)建模為一個矩陣S，假設(shè)該矩陣包括了h個社團(tuán)，首先初始化矩陣S的m個特征值為社團(tuán)的核心節(jié)點，也即是聚類中心，則h個社團(tuán)的K均值算法矩陣如公式（1）所示：

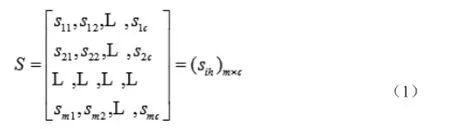
在K均值算法聚類執(zhí)行過程中，可以設(shè)置不同的特征權(quán)重，一般能夠優(yōu)化突出較為重要的特征貢獻(xiàn)，特征權(quán)重向量如公式（2）所示：

通過分析，K均值聚類的目標(biāo)函數(shù)如公式（3）所示：

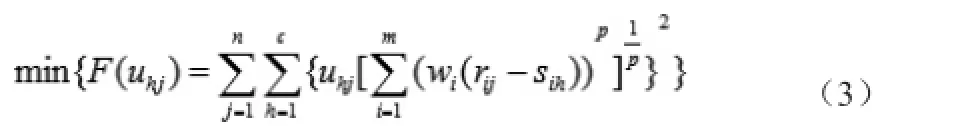
在復(fù)雜網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)過程中，K均值算法可以迭代執(zhí)行，直到獲取最優(yōu)解或次優(yōu)解，滿足人們的需求。

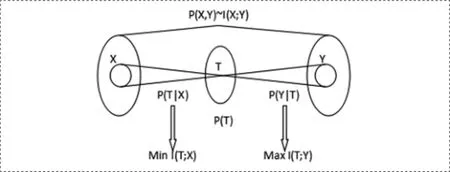
圖2 社團(tuán)發(fā)現(xiàn)原理

3.3信息論算法

假設(shè)復(fù)雜網(wǎng)絡(luò)X包含T個社團(tuán)，每一個社團(tuán)都存在Y個相關(guān)變量進(jìn)行度量，因此社團(tuán)發(fā)現(xiàn)可以使用信息論進(jìn)行形式化描述：給定變量X和相關(guān)變量Y及其聯(lián)合概率分布P（X，Y），在將變量X中的節(jié)點壓縮到T個社團(tuán)中時，需要盡可能的保存相關(guān)變量Y的信息，也即是盡可能的最小化互信息I（X；T）且最大化保存互信息I（Y；T），社團(tuán)發(fā)現(xiàn)過程如圖2所示。

利用互信息開展社團(tuán)發(fā)現(xiàn)的目標(biāo)函數(shù)可以設(shè)置為公式（4）。

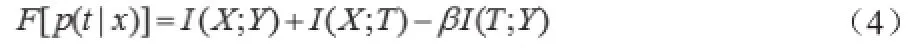
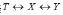
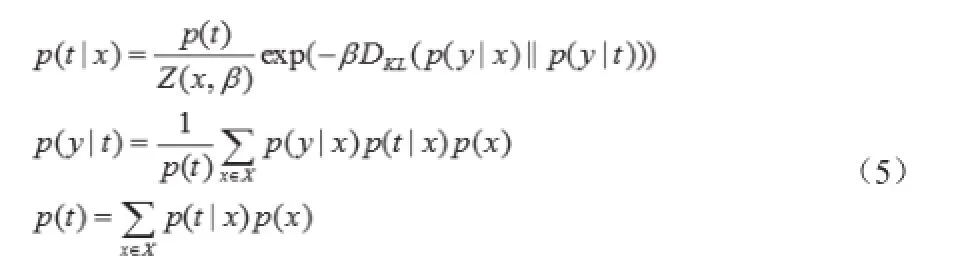
4.結(jié)束語

社團(tuán)發(fā)現(xiàn)可以有效處理復(fù)雜網(wǎng)絡(luò)信息，尋求人們期望的知識。社團(tuán)發(fā)現(xiàn)已經(jīng)在電子商務(wù)推薦系統(tǒng)、社交網(wǎng)絡(luò)服務(wù)系統(tǒng)、輿情信息研判分析系統(tǒng)中得到廣泛普及和使用，利用聚類算法可以提高這些系統(tǒng)的準(zhǔn)確度，為人們提供更好的服務(wù)。

［1］黃健斌，孫鶴立，Dustin BORTNER，等.從鏈接密度遍歷序列中挖掘網(wǎng)絡(luò)社團(tuán)的層次結(jié)構(gòu)［J］.軟件學(xué)報，2011，22（5）：951-961.

［2］賈宗維，崔軍.一種發(fā)現(xiàn)社團(tuán)結(jié)構(gòu)的快速凝聚聚類算法［J］.湘潭大學(xué)自然科學(xué)學(xué)報，2012，34（4）：103-107.

［3］董哲，伊鵬.采用鏈路聚類的動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)算法［J］.西安交通大學(xué)學(xué)報，2014，48（8）：73-79.

［4］付立東.核k-means聚類檢測復(fù)雜網(wǎng)絡(luò)社團(tuán)算法［J］.計算機(jī)科學(xué)，2010，37（9）：212-213.一化函數(shù)。從解空間的定義看以得出，目標(biāo)函數(shù)的具有一個形式解，如果想得到具體的解，還需要借助具體的算法等。