航空發動機魯棒PI控制頻域設計

唐鈺婷，仇小杰

（中航工業航空動力控制系統研究所，江蘇無錫214063）

航空發動機魯棒PI控制頻域設計

唐鈺婷，仇小杰

（中航工業航空動力控制系統研究所，江蘇無錫214063）

針對航空發動機高、低壓轉速和壓比控制回路，研究中考慮執行機構動態的高階開環傳遞函數，根據推廣到時滯系統的棱邊定理，采用頻域方法設計有參數不確定性的非精確模型的魯棒PI控制器；并利用不確定范圍內的發動機非線性模型構成的棱邊系統和不確定系統族，驗證了魯棒控制器作用下的系統性能。仿真結果表明，該頻域設計方法能使閉環系統的性能指標和魯棒性均達標。

航空發動機；高階系統；魯棒PI控制；頻域設計；棱邊定理；參數不確定性；時滯系統

1　引言

工程中很難精確描述實際的控制系統，因此所得系統模型常常存在不確定因素。對于航空發動機，建模時的近似、發動機的非線性失真、發動機和執行機構個體間的差異等，都會為系統帶來不確定性。此外，發動機性能衰減、元件老化、外部干擾和噪聲、環境因素也會為系統帶來不確定性。當以上不確定因素對系統造成的影響不可忽略時，就必須將其納入控制系統設計的考慮范圍。而基于有不確定性的非精確模型設計控制器時，魯棒控制就成為一種重要的解決方法［1-2］。魯棒控制于1972年首次提出，隨后出現了Kharitonov定理［3］、棱邊定理、小增益定理、結構奇異值理論、H∞理論［4-5］等理論和方法。

PID控制是國內外現役航空發動機控制系統廣泛采用的一種方法［6］，對其結構的研究并未隨著時間的推移減弱，而是日益受到重視［7］。PID控制中的一個關鍵問題是控制參數的整定，控制質量和控制器的魯棒性都直接受到整定好壞的影響［8］。而通過頻域設計整定控制參數，可兼顧對系統響應動態和抑制噪聲的要求，具有良好的頻域特性，對噪聲和干擾的魯棒性較好。

本文根據推廣到時滯系統的棱邊定理，研究航空發動機控制系統的魯棒PI控制頻域設計方法，設計有參數不確定性的非精確模型的魯棒PI控制器。通過PI控制參數的穩定域算法，確定棱邊系統的魯棒PI控制參數集，并利用不確定范圍內的發動機非線性模型構成的棱邊系統和不確定系統族，驗證魯棒控制器作用下的系統性能。

2　魯棒PID控制器頻域設計

考慮一類時滯系統，可用下述公式描述：

其特征方程可用下述n階準多項式描述：

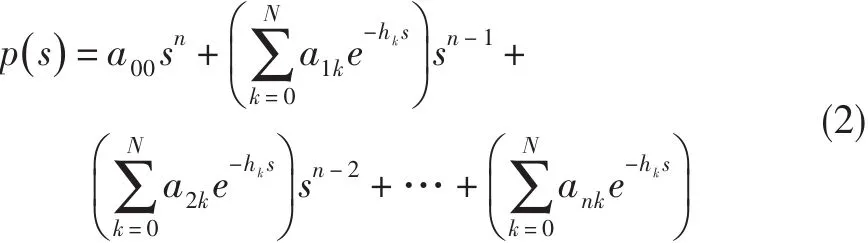
式中：aik=αik+jβik，αik、βik∈R為常數，a00≠0， 0=h0＜h1＜h2＜…＜hN為對應于系統時滯的常量。

定義1［9］假設復平面上有一區域D，當式（2）中的特征準多項式p（ s）的所有零點都在D中時，時滯系統（1）被稱為D-穩定的。特別地，如果p（s）為D-穩定的，且D為左半平面，則稱p（s）為穩定的。

假設式（2）中p（s）的系數包含不確定因素，則需要關注的就是在考慮了所有可容許的參數攝動的情況下確定D-穩定性。考慮下述一族n階（實數或復數）準特征多項式：

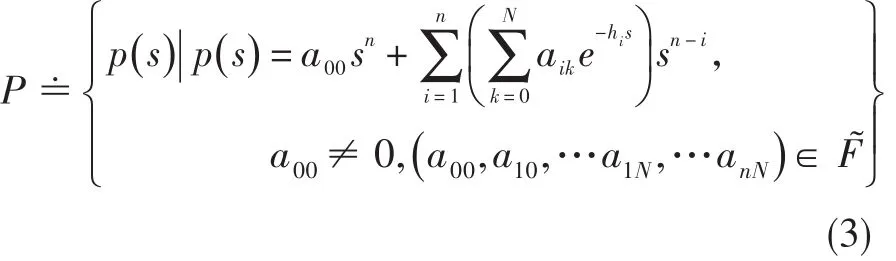
式中：conv表示凸生成。如果P為實數準多項式族，則每個準多項式）的首項系數必須同號［9］。

引理1［9］考慮如式（3）的n階準多項式多面體P和復平面上的任一區域D滿足如下條件：x和y分別為復平面上的兩點，存在實數α，對任意一點x∈Dc（Dc為D在復平面的補集）和任意M＞0，若有且 Rey≥α，則可以在Dc內找到一條連續的路徑由x通向y。則當且僅當多面體P的所有棱邊均是D-穩定時，多面體P才是D-穩定的。

對于式（1）形式的時滯系統，設有有限個數的傳遞函數

則不確定模型組成的所有凸生成，即不確定時滯系統族為：

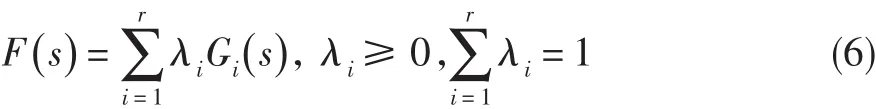
定理1［9］考慮式（6）所示的參數不確定系統族，設計PI控制器進行控制，使該不確定系統族穩定，當且僅當用同一PI控制器使得系統族中每一個）都穩定。

證明［9］考慮有限個數的開環傳遞函數

3　發動機轉速和壓比系統魯棒控制頻域設計

3.1轉速系統魯棒控制頻域設計

假設燃油量-轉速線性模型的傳遞函數為包含兩個極點一個零點的二階動態系統，主燃油執行機構的傳遞函數為帶滯后因子的一階慣性環節，則對于燃油量-轉速有：

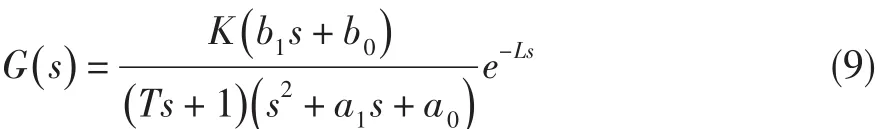
式中：a1、a0、b1、b0為常數，K＞0為執行機構穩態增益，L＞0為執行機構滯后時間，T為執行機構時間常數。為簡便快速地驗證魯棒控制頻域設計方法的有效性，假設攝動的不確定參數為K和T。根據K和T的攝動范圍可得到若干個棱邊系統：

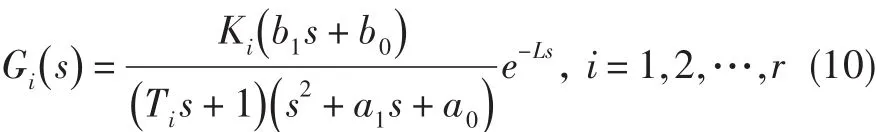
根據文獻［10］中PI控制參數的穩定域算法，可得到這若干個棱邊系統各自對應的穩定區域。由定理1可知，G（s）穩定的充分必要條件即為這若干個棱邊系統同時穩定。換言之所求的PI控制器的穩定區域，即為這若干個棱邊系統穩定區域的交集，該交集內的控制器參數均能使系統（9）穩定。在此交集內選擇能同時滿足系統族各種性能指標的控制參數，即可達到期望的控制要求。

3.2壓比系統魯棒控制頻域設計

假設噴口面積-壓比線性模型的傳遞函數為包含兩個極點兩個零點的二階動態系統，執行機構的傳遞函數為帶滯后因子的一階慣性環節，則對于噴口面積-壓比有：

式中：b2為常數，其余同式（9）。同樣，根據K和T的攝動范圍可得到若干個棱邊系統：

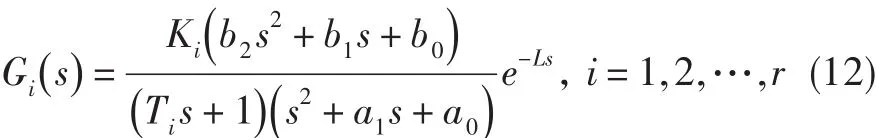
在這若干個棱邊系統穩定區域的交集上選擇能同時滿足系統族各種性能指標的控制參數，即可達到期望的控制要求。

4　仿真算例

以海平面1.0馬赫數條件下的轉速控制系統為例，發動機中間狀態的燃油量-高壓轉速線性模型為：

主燃油執行機構的傳遞函數為：

設執行機構的K和T的攝動范圍均為±20%，由式（10）可得如下4個棱邊系統：

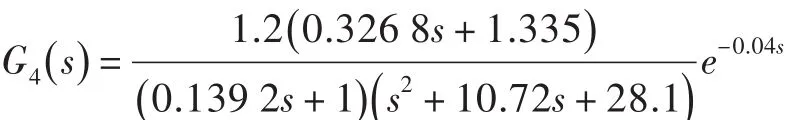
按照文獻［10］的方法，分別畫出這4個棱邊系統所對應的PI控制參數穩定域，見圖1。圖中陰影部分為穩定域的交集，即目標的參數穩定域。為更快找到合適的控制參數，給棱邊系統以一定的幅值裕度和相角裕度要求得到范圍更小的目標參數區域，見圖2。

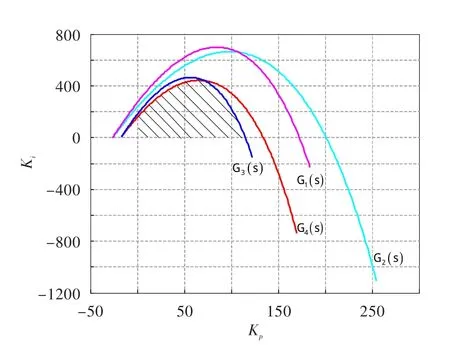
圖1　棱邊系統的控制參數穩定域Fig.1 Control parameter stability region of edge systems

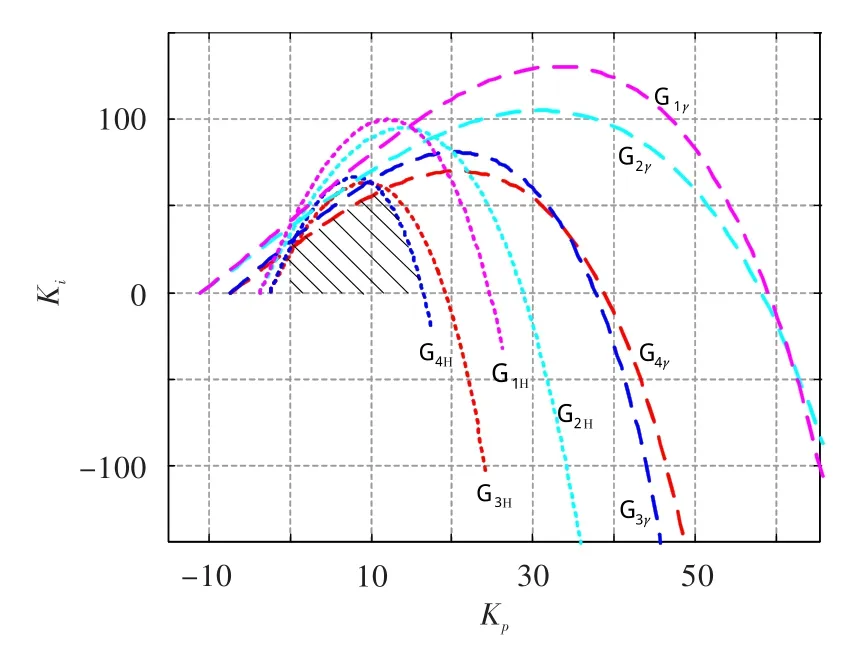
圖2　滿足幅值裕度和相角裕度的棱邊系統穩定域Fig.2 Control parameter stability region satisfied the required stability margin of edge systems

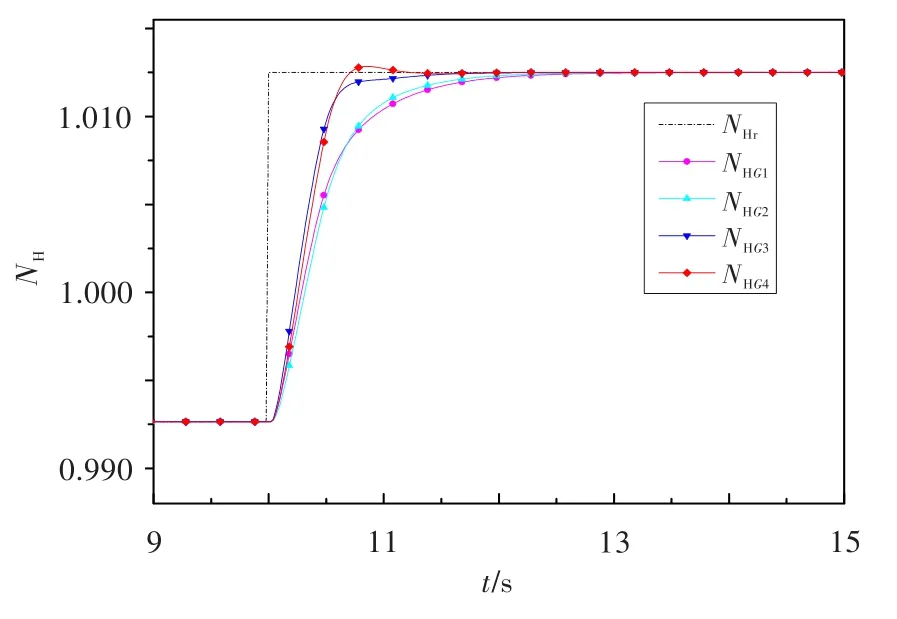
圖3　各棱邊系統高壓轉速階躍響應Fig.3 High pressure rotor speed response of edge systems

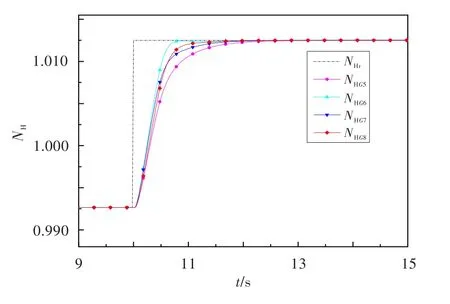
圖4　不確定系統族的高壓轉速階躍響應Fig.4 High pressure rotor speed response of uncertain system family

同理，可得到該點中間狀態燃油量-低壓轉速的4個棱邊系統穩定區域的交集，由此得到魯棒控制參數，相應的棱邊系統和驗證系統的仿真結果見圖5和圖6。圖中，NLr為給定低壓轉速，NLG1～NLG4分別為燃油量-低壓轉速4個棱邊系統的低壓轉速響應，NLG5～NLG8分別為燃油量-低壓轉速4個驗證系統的低壓轉速響應。由圖5可知，各系統均能達到穩定，響應中超調量最大的是G4（）s，不超過1.975%；調節時間最長的是G1（）s，不超過1.48 s，能滿足期望的性能要求。由圖6可看出，4個驗證系統均達到了穩定的超調量最大為0.400%，的調節時間最長為1.40 s，控制效果較好。

圖5　各棱邊系統低壓轉速階躍響應Fig.5 Low pressure rotor speed response of edge systems

圖6　不確定系統族的低壓轉速階躍響應Fig.6 Low pressure rotor speed response of uncertain system family

以海平面1.0馬赫數條件下的壓比控制系統為例，發動機中間狀態的噴口面積-壓比線性模型為：

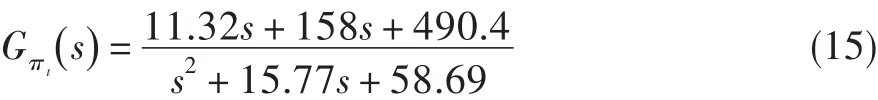
執行機構的傳遞函數采用以下形式：

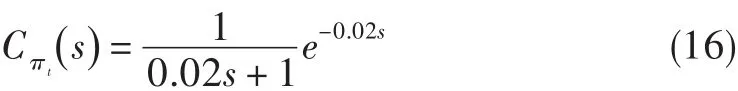
設執行機構的K和T的攝動范圍均為±20%，采用類似于上述的方法，分別畫出4個棱邊系統所對應的PI控制參數穩定區域，并給以一定的幅值裕度和相角裕度要求，得到穩定區域的交集。選擇魯棒控制參數相應的棱邊系統和驗證系統的仿真結果見圖7和圖8。圖中，πtr為給定壓比，πtG1～πtG4分別為噴口面積-壓比4個棱邊系統的壓比響應，πtG5～πtG8分別為噴口面積-壓比4個驗證系統的壓比響應。由圖7可知，各系統均能達到穩定，響應均無超調；調節時間最長的是G1（）s，不超過0.400 s，能滿足期望的性能要求。從圖8可看出，4個驗證系統均達到了穩定，響應均無超調，G5（）s的調節時間最長為0.400 s，控制效果良好。

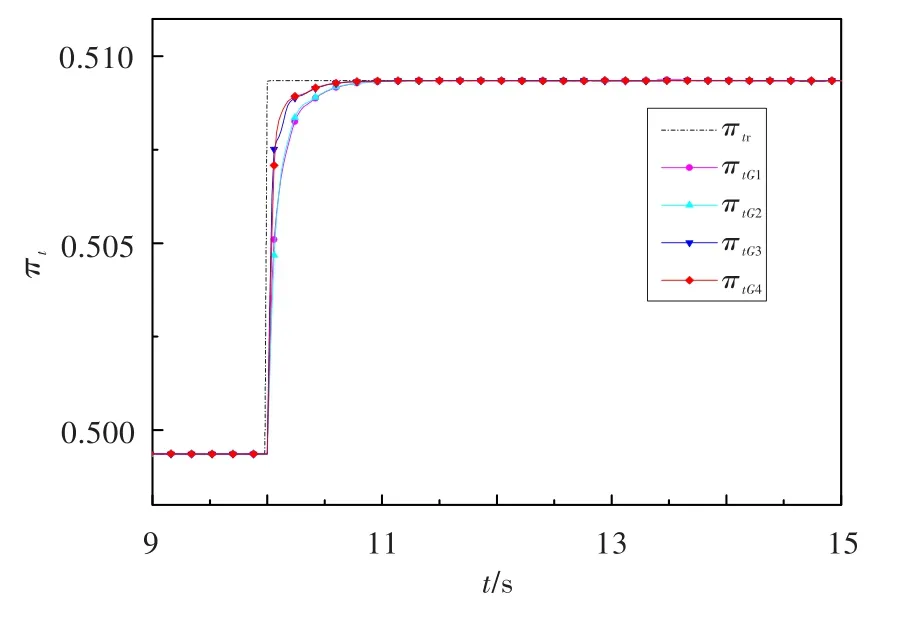
圖7　各棱邊系統壓比階躍響應Fig.7 Pressure ratio response of edge systems

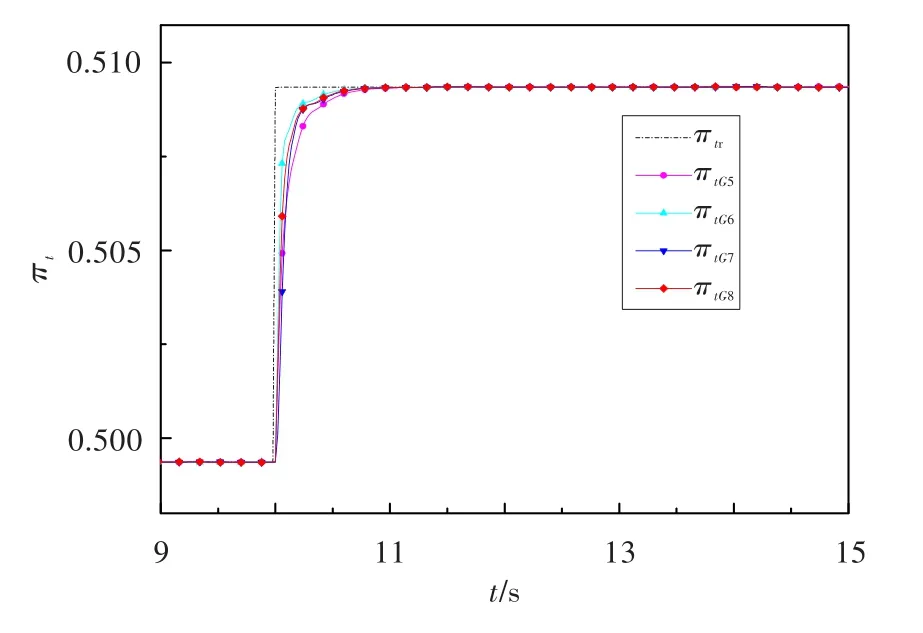
圖8　不確定系統族的壓比階躍響應Fig.8 Pressure ratio response of uncertain system family

5　結束語

本文將實際的航空發動機控制中將出現不確定因素的問題納入考慮，針對發動機轉速控制系統和壓比控制系統，利用頻域方法設計基于有不確定性的非精確模型的魯棒控制器。根據推廣到時滯系統的棱邊定理，一個高維準多項式多面體的穩定性問題可轉化成若干個多面體棱邊系統的穩定性問題，求得這些棱邊系統的穩定域交集即可得到不確定系統族的控制參數取值范圍。并以具體工作點的轉速和壓比作為被控對象，給系統參數以一定的變化，在穩定域的交集上選擇能使控制系統達到性能指標的魯棒控制參數，利用在不確定范圍里的系統驗證了魯棒控制器作用下的系統性能。非線性模型仿真結果表明，該頻域設計方法得到的魯棒控制參數的控制效果較好，擴大了航空發動機控制系統頻域設計的適用范圍，具有較好的應用前景。

［1］ Silva G J，Datta A，Bhattacharyya S P.On the stability and controller robustness of some popular PID tuning rules［J］. IEEE Trans.on Automatic Control，2003，48（9）：1638—1641.

［2］ Silva G J，Datta A，Bhattacharyya S P.Robust control de?sign using the PID controller［C］//.Proc.of the 41st IEEE Conf.on Decision and Control.2002.

［3］ Kharitonov V L.Asymptotic stability of an equilibrium po?sition of a family of systems of linear differential equations ［J］.Differential Uravnen.，1978，14：2086—2088.

［4］ Kimura H.Robust stability for a class of transfer functions ［J］.IEEE Trans.on Automatic Control，1984，29（9）：788—793.

［5］ Doyle J，Glover K，Khargonekar P，et al.State space solu?tion to standardH2andH∞control problem［J］.IEEE Trans.on Automatic Control，1989，34（8）：831—847.

［6］ 孫健國.面向21世紀航空動力控制展望［J］.航空動力學報，2001，16（2）：97—102.

［7］ Isaksson A，Hagglund T.Editorial PID control［J］.IEE. Proc.Control Theory Appl.，2002，149（1）：1—2.

［8］ Wang Q G，Lee T H，Fung H W，et al.PID tuning for im?proved performance［J］.IEEE Transactions on Control Sys?tem Technology，1999，7（4）：457—465.

［9］ Minyue F，Andrzej W O，Michael P P.Robust stability for time-delay systems：the edge theorem and graphical tests ［J］.IEEE Trans.on Automatic Control，1989，34（8）：813—820.

［10］唐鈺婷，黃金泉，潘慕絢.基于幅相裕度頻域法PI參數最優整定方法［C］//.中國航空學會第十六屆航空發動機自動控制專業學術會議論文集.2012.

Frequency domain design of robust PI control for aero-engine

TANG Yu-ting，QIU Xiao-jie

（AVIC Aviation Motor Control System Institute，Wuxi 214063，China）

For the aero-engine high and low pressure rotor speed control loops and pressure ratio control loop，considering dynamic high order open loop transfer function of execute mechanism，the frequency do?main method of designing the robust PI controller for the non-exact models with parameter uncertainties was researched，which based on the edge theorem extended to time-delay systems；then the edge systems and the uncertain system family contained the engine nonlinear model that in the range of uncertainty were used to validate the system performance under the robust controller.Simulation results demonstrate that the design method satisfies performance indices and robustness of closed loop system.

aero-engine；high order system；robust PI control；frequency domain design；edge theorem；parametric uncertainty；time-delay system

V233.7+3

A

1672-2620（2016）04-0038-05

2016-05-30；

2016-08-13

唐鈺婷（1988-），女，河南滑縣人，助理工程師，碩士，從事航空發動機控制研究。