大氣相干長(zhǎng)度的瞬時(shí)測(cè)量

衛(wèi)沛鋒，林旭東，王　亮，王鳴浩

(1.中國(guó)科學(xué)院 長(zhǎng)春光學(xué)精密機(jī)械與物理研究所，吉林 長(zhǎng)春130033； 2.中國(guó)科學(xué)院大學(xué)，北京 100049)

?

大氣相干長(zhǎng)度的瞬時(shí)測(cè)量

衛(wèi)沛鋒1,2*，林旭東1，王亮1，王鳴浩1

(1.中國(guó)科學(xué)院 長(zhǎng)春光學(xué)精密機(jī)械與物理研究所，吉林 長(zhǎng)春130033； 2.中國(guó)科學(xué)院大學(xué)，北京 100049)

由于差分像運(yùn)動(dòng)監(jiān)測(cè)法測(cè)量大氣相干長(zhǎng)度需要多幀統(tǒng)計(jì)，本文應(yīng)用波前結(jié)構(gòu)函數(shù)法，提出了一種大氣相干長(zhǎng)度的瞬時(shí)測(cè)量方法。該方法通過(guò)Shack-Hartmann波前探測(cè)器測(cè)量單幀短曝光畸變波前的Zernike系數(shù);然后減去光學(xué)系統(tǒng)初始像差的Zernike系數(shù)，去除傾斜項(xiàng)，計(jì)算波前結(jié)構(gòu)函數(shù);最后,與滿(mǎn)足Kolmogorov湍流理論的大氣短曝光理論波前結(jié)構(gòu)函數(shù)進(jìn)行最小二乘擬合，得到瞬時(shí)大氣相干長(zhǎng)度。利用湍流相位板構(gòu)造了相應(yīng)的測(cè)試系統(tǒng)，并進(jìn)行了外場(chǎng)實(shí)測(cè)對(duì)比。結(jié)果表明：提出的基于波前結(jié)構(gòu)函數(shù)法的測(cè)量結(jié)果與差分像運(yùn)動(dòng)監(jiān)測(cè)法的測(cè)量結(jié)果基本吻合；不同格林伍德頻率下，標(biāo)準(zhǔn)差與均值之比小于4.1%，穩(wěn)定性較好；外場(chǎng)比對(duì)累計(jì)16個(gè)夜晚，得到的平均偏差小于0.45 cm。該方法可以實(shí)現(xiàn)空間目標(biāo)大氣相干長(zhǎng)度的單幀瞬時(shí)測(cè)量，并可用于觀測(cè)站點(diǎn)的視寧度、自適應(yīng)光學(xué)系統(tǒng)內(nèi)部大氣湍流強(qiáng)度和地基大口徑望遠(yuǎn)鏡主鏡視寧度的監(jiān)測(cè)。

自適應(yīng)光學(xué)；大氣相干長(zhǎng)度；空間目標(biāo);瞬時(shí)測(cè)量;波前結(jié)構(gòu)函數(shù)法

*Correspondingauthor,E-mail:weipeifeng@gmail.com

1　引　言

為獲取天文目標(biāo)和空間目標(biāo)的清晰圖像，地基望遠(yuǎn)鏡口徑越來(lái)越大，但其分辨率卻受限于大氣相干長(zhǎng)度。為克服大氣對(duì)望遠(yuǎn)鏡分辨能力的限制，自適應(yīng)光學(xué)系統(tǒng)已經(jīng)成為地基大口徑望遠(yuǎn)鏡必不可少的技術(shù)單元[1-2]。

天文學(xué)家一般用大氣相干長(zhǎng)度r0或者視寧度來(lái)表征大氣在空域上對(duì)望遠(yuǎn)鏡分辨率的限制。大氣相干長(zhǎng)度定義為位相起伏的均方值為1 rad的圓域或子孔徑的大小,國(guó)際上一般用差分像運(yùn)動(dòng)監(jiān)測(cè)法(Differential Image Motion Monitor,DIMM)來(lái)測(cè)量r0[3]。該方法的實(shí)質(zhì)是依據(jù)湍流凍結(jié)假設(shè)用差分到達(dá)角的時(shí)域起伏方差來(lái)獲取大氣畸變波前的空域統(tǒng)計(jì)特征量r0。DIMM的測(cè)量結(jié)果與目標(biāo)仰角相關(guān)，且一般需要一分鐘或數(shù)百幀的數(shù)據(jù)來(lái)獲取一個(gè)有效數(shù)據(jù)，觀測(cè)目標(biāo)多為靜止不動(dòng)或運(yùn)動(dòng)很慢的恒星或行星目標(biāo)，所以不適用于監(jiān)測(cè)仰角變化快、觀測(cè)時(shí)間短的空間目標(biāo)。空間目標(biāo)的大氣相干長(zhǎng)度如何變化，是否遵循理論上與目標(biāo)觀測(cè)仰角正割的6/5方成正比，以及量級(jí)都有待進(jìn)一步地明確。

1975年，F(xiàn)ried推導(dǎo)了差分到達(dá)角起伏的方差公式[4]，該公式成為差分像運(yùn)動(dòng)監(jiān)測(cè)法的基本原理。1990年，M.Sarazin通過(guò)40 s200 frame的連續(xù)曝光來(lái)監(jiān)測(cè)大氣相干長(zhǎng)度[5-6]。2000年，饒瑞中采用三星點(diǎn)像運(yùn)動(dòng)法[7]來(lái)測(cè)量大氣相干長(zhǎng)度，并于2007年提出了改進(jìn)的四孔差分星點(diǎn)像運(yùn)動(dòng)法[8]。2010年，他們采用該方法對(duì)Dome效應(yīng)進(jìn)行了監(jiān)測(cè)，計(jì)算樣本數(shù)為200 frame，測(cè)量時(shí)間為3 s[9]。2013年，陳浩[10]通過(guò)將一對(duì)星點(diǎn)像增加為Shack-Hartmann波前探測(cè)器上呈正方形分布的十二對(duì)星點(diǎn)像來(lái)增加空間統(tǒng)計(jì)特征，計(jì)算樣本數(shù)為300 frame。上述方法的改進(jìn)思路類(lèi)似，都是通過(guò)增加空間統(tǒng)計(jì)特性來(lái)提高測(cè)量結(jié)果的穩(wěn)定性。2014年,黃德權(quán)[11]提出通過(guò)波前分布的時(shí)域剩余方差來(lái)計(jì)算大氣相干長(zhǎng)度，同樣需要一定的觀測(cè)時(shí)間和幀數(shù)。因此，上述方法均不適用于測(cè)量角度變化快、觀測(cè)時(shí)間短的空間目標(biāo)的大氣相干長(zhǎng)度。

本文利用Shack-Hartmann波前探測(cè)器測(cè)量的單幀短曝光畸變波前的Zernike系數(shù)，計(jì)算大氣波前結(jié)構(gòu)函數(shù)，通過(guò)與理論結(jié)果對(duì)比來(lái)獲取瞬時(shí)大氣相干長(zhǎng)度。并利用可控制、可重復(fù)的湍流相位板構(gòu)造了相應(yīng)的自適應(yīng)光學(xué)測(cè)試系統(tǒng)，對(duì)該算法進(jìn)行驗(yàn)證。同時(shí)，還進(jìn)行了累計(jì)16個(gè)有效觀測(cè)夜晚的實(shí)測(cè)比對(duì)。

2　波前結(jié)構(gòu)函數(shù)法測(cè)量瞬時(shí)大氣相干長(zhǎng)度的原理

對(duì)于多數(shù)觀測(cè)時(shí)間只有1～2分鐘、且仰角快速變化的空間目標(biāo)來(lái)講，如果能直接提取空域統(tǒng)計(jì)信息，就可實(shí)現(xiàn)r0的瞬時(shí)測(cè)量。而波前結(jié)構(gòu)函數(shù)是波前在光瞳面上的空域一維二階統(tǒng)計(jì)量，這里設(shè)法從波前結(jié)構(gòu)函數(shù)提取r0。

結(jié)構(gòu)函數(shù)定義為不同空間間隔下成對(duì)點(diǎn)之間的波前相位差的平方的統(tǒng)計(jì)均值，即有：

Dφ(r)=〈[φ(x+r)-φ(x)]2〉x,

(1)

式中：r為成對(duì)點(diǎn)之間的空間間隔，φ為相應(yīng)位置的波前相位，x表示光瞳面上的空間位置，三角括號(hào)表示所有x處的統(tǒng)計(jì)平均。

Shack-Hartmann是目前自適應(yīng)光學(xué)系統(tǒng)最常用的波前探測(cè)器。通過(guò)波前解析可以得到短曝光單幀畸變波前的Zernike系數(shù)，從而可得到對(duì)應(yīng)的波前結(jié)構(gòu)函數(shù)的測(cè)量值。另外，短曝光條件下，滿(mǎn)足Kolmogorov湍流模型的理論大氣畸變波前的結(jié)構(gòu)函數(shù)為[12]：

(2)

式中：d為望遠(yuǎn)鏡主鏡口徑，2σ2代表大氣散射損失，這里忽略不計(jì)。對(duì)不同大氣相干長(zhǎng)度對(duì)應(yīng)的波前結(jié)構(gòu)函數(shù)的理論值和測(cè)量值進(jìn)行最小二乘擬合，便可求解得到瞬時(shí)的大氣相干長(zhǎng)度，此時(shí)測(cè)得的是對(duì)應(yīng)目標(biāo)觀測(cè)仰角處的大氣相干長(zhǎng)度。而望遠(yuǎn)鏡觀測(cè)站點(diǎn)的整層大氣相干長(zhǎng)度須歸一化到天頂角處來(lái)進(jìn)行監(jiān)測(cè)，所以須對(duì)式(2)進(jìn)行修正：

(3)

式中：ζ為天頂角，r0′ 為式(2)的測(cè)量結(jié)果。

瞬時(shí)大氣相干長(zhǎng)度的計(jì)算流程如下：(1)獲取Shack-Hartmann測(cè)量的短曝光(曝光時(shí)間須小于大氣相干時(shí)間)單幀畸變波前的Zernike系數(shù)；(2)減去光學(xué)系統(tǒng)初始像差的Zernike系數(shù)；(3)計(jì)算測(cè)量波前去除傾斜項(xiàng)后對(duì)應(yīng)的結(jié)構(gòu)函數(shù)；(4)按式(2)計(jì)算對(duì)應(yīng)r0從0.01～10 m間隔為0.001 m對(duì)應(yīng)的理論波前結(jié)構(gòu)函數(shù)；(5)對(duì)比結(jié)構(gòu)函數(shù)的理論值與測(cè)量值，求大氣相干長(zhǎng)度的最小二乘估計(jì)；(6)如果需要監(jiān)測(cè)天頂角處的r0，按式(3)進(jìn)行修正。

3　實(shí)　驗(yàn)

為驗(yàn)證上述算法，采用湍流相位板模擬大氣湍流構(gòu)造了一套自適應(yīng)光學(xué)測(cè)試系統(tǒng)，光路如圖1所示。25 μm直徑的白光光纖光源Source發(fā)出的光經(jīng)過(guò)湍流相位板形成隨機(jī)波前。隨機(jī)波前經(jīng)平面鏡1轉(zhuǎn)折光路后再經(jīng)透鏡L1變?yōu)槠叫泄馊肷涞娇焖俜瓷溏R(Fast Steering Mirror，F(xiàn)SM)上，然后反射到變形鏡(Deformable Mirror，DM)上，經(jīng)透鏡L2會(huì)聚和分色片透射后在CCD上成像。分色片反射的光經(jīng)透鏡L3準(zhǔn)直后入射到Shack-Hartmann波前探測(cè)器中。

圖1　自適應(yīng)光學(xué)測(cè)試系統(tǒng)光路圖Fig.1　Scheme of adaptive optics testing system

實(shí)驗(yàn)光路中，F(xiàn)SM、DM和波前探測(cè)器均為自研，DM為97單元壓電變形鏡。Shack-Hartmann的曝光時(shí)間為1.98 ms，有效點(diǎn)數(shù)為97。湍流相位板為從Lexitek公司定制的相干長(zhǎng)度為0.6 mm(@633 nm)的隨機(jī)相位板，相位分布滿(mǎn)足Kolmogrov湍流理論。通過(guò)改變湍流相位板的通光尺寸來(lái)模擬r0的變化。其原理如下[13]：

(3)

式中：D為模擬的望遠(yuǎn)鏡口徑；r0′為湍流相位板的相干長(zhǎng)度；D′為湍流相位板上的通光孔徑尺寸。通過(guò)調(diào)節(jié)湍流相位板的轉(zhuǎn)速來(lái)模擬格林伍德頻率fG的變化，fG與湍流相位板轉(zhuǎn)速的關(guān)系為：

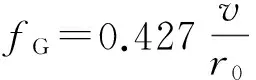
(4)

式中v為通光孔徑中心處的線速度。

4　討　論

Shack-Hartmann波前探測(cè)器受0.6 mm湍流相位板影響的點(diǎn)列圖如圖2所示。由圖2可看出，湍流相位屏的加入使得原先亮度均勻、排列整齊、大小相同的點(diǎn)變得明暗不均、排列錯(cuò)位、大小不一。

(a) 無(wú)湍流相位板　　(b)0.6 mm湍流相位板(a) Without phase plate 　(b) With 0.6 mm phase plate圖2　Shack-Hartmann波前探測(cè)器點(diǎn)列圖Fig.2　Spot arrays of Shack-Hartmann wavefront sensor

大氣的格林伍德頻率fG約為50～90 Hz，內(nèi)陸地區(qū)的r0一般小于10 cm，因此，調(diào)整湍流相位板轉(zhuǎn)速使得模擬的fG為60 Hz，調(diào)整通光孔徑r0為9 cm。采用本文所述方法計(jì)算模擬的湍流波前。首先，使Shack-Hartmann曝光時(shí)間小于大氣相干時(shí)間(一般約為10 ms)，這里為1.98 ms，得到畸變波前的Zernike系數(shù)；通過(guò)設(shè)置參考或直接減去光學(xué)系統(tǒng)初始像差，得到大氣畸變波前的Zernike系數(shù)；預(yù)先計(jì)算得到不同項(xiàng)單位Zernike系數(shù)的結(jié)構(gòu)函數(shù)，然后與大氣畸變波前Zernike系數(shù)相乘后累加，計(jì)算去除傾斜項(xiàng)后對(duì)應(yīng)的結(jié)構(gòu)函數(shù)；按式(2)計(jì)算對(duì)應(yīng)的理論波前結(jié)構(gòu)函數(shù)；最后，通過(guò)對(duì)比波前結(jié)構(gòu)函數(shù)的理論值與測(cè)量值，求得大氣相干長(zhǎng)度的最小二乘估計(jì)。實(shí)驗(yàn)中，光束相當(dāng)于直接從天頂角處入射，計(jì)算結(jié)果無(wú)須進(jìn)行角度修正，但實(shí)際外場(chǎng)測(cè)量時(shí)則必需進(jìn)行角度修正。8 625幀的湍流波前的測(cè)量結(jié)果如圖3所示。由于r0與波長(zhǎng)相關(guān)，故后續(xù)計(jì)算結(jié)果統(tǒng)一歸一化到633 nm，以便于比較。r0測(cè)量均值為9.6 cm，標(biāo)準(zhǔn)差為3.6 cm，波動(dòng)較大。圖4為Shack-Hartmann測(cè)量的波前均方差(Root Mean of Square,RMS)，RMS均值為0.454 6λ(λ=633 nm)，標(biāo)準(zhǔn)差為0.1λ，同樣波動(dòng)較大。對(duì)比圖3和圖4說(shuō)明：瞬時(shí)r0的測(cè)量結(jié)果同波前均方差RMS波動(dòng)的周期性、幅度均類(lèi)似，能較好地反映波前的瞬時(shí)變化特征，這也正是波前結(jié)構(gòu)函數(shù)法測(cè)量r0的優(yōu)勢(shì)。

圖3　fG=60 Hz，r0=9 cm時(shí)波前結(jié)構(gòu)函數(shù)法的測(cè)量結(jié)果Fig.3　Result of wavefront structure function when fG=60 Hz and r0=9 cm

圖4　fG=60 Hz，r0=9 cm時(shí)波前均方差RMS的變化Fig.4　Variation of RMS of wavefront when fG=60 Hz and r0=9 cm

測(cè)量均值r0=9.6 cm與設(shè)計(jì)值r0=9 cm的波前結(jié)構(gòu)函數(shù)的對(duì)比如圖5所示。從圖5可看出，測(cè)量均值與設(shè)計(jì)值的波前結(jié)構(gòu)函數(shù)能夠較好地吻合；但是在大的空間間隔，即低頻處的偏差稍大。其原因有兩方面：一方面是大氣湍流理論模型引起的偏差。式(2)的理論前提是大氣湍流滿(mǎn)足Kolmogorov湍流模型，但實(shí)際的大氣湍流并不完全遵從該理論[14]；另一方面，計(jì)算結(jié)構(gòu)函數(shù)時(shí)低頻處的統(tǒng)計(jì)樣本數(shù)小于高頻處會(huì)引起部分統(tǒng)計(jì)偏差。

圖5　波前結(jié)構(gòu)函數(shù)的測(cè)量值和理論值對(duì)比Fig.5　Comparison between theoretical values and experimental values of wavefront structure function

為驗(yàn)證波前結(jié)構(gòu)函數(shù)法測(cè)量瞬時(shí)r0的準(zhǔn)確性和穩(wěn)定性，同時(shí)模擬了r0=11,9,5 cm，fG=10～100 Hz，間隔10 Hz時(shí)的波前結(jié)構(gòu)函數(shù)法和DIMM法測(cè)量r0的結(jié)果比較。為增加DIMM測(cè)量結(jié)果的穩(wěn)定性，選取圖2所示的Shack-Hartmann點(diǎn)列圖中第4～8行，第3列、第11列共5對(duì)點(diǎn)的統(tǒng)計(jì)平均值作為DIMM方法的測(cè)量結(jié)果。兩種方法的測(cè)量結(jié)果對(duì)比如圖6所示，圖中實(shí)線為設(shè)計(jì)值，點(diǎn)劃線為擬合曲線。由圖6可看出，波前結(jié)構(gòu)函數(shù)法的測(cè)量結(jié)果同DIMM法測(cè)量結(jié)果呈良好的線性關(guān)系，并且隨著模擬r0的變化，能同步反映波前的變化；但兩種方法的測(cè)量值存在一定的偏差，這是由于DIMM方法固有的空間采樣不足的缺陷，或者理論波前結(jié)構(gòu)函數(shù)模型描述誤差引起的；兩種方法的測(cè)量值都同設(shè)計(jì)值存在一定的偏差，這可能是實(shí)驗(yàn)過(guò)程中通光孔徑尺寸的設(shè)置偏差所引起的。從圖6還可看出，在模擬大氣湍流r0一定的情況下，當(dāng)fG從10 Hz變化到100 Hz時(shí)，波前結(jié)構(gòu)函數(shù)法測(cè)量的瞬時(shí)r0的標(biāo)準(zhǔn)差與均值之比的最大值小于4.1%，說(shuō)明測(cè)量穩(wěn)定性良好。

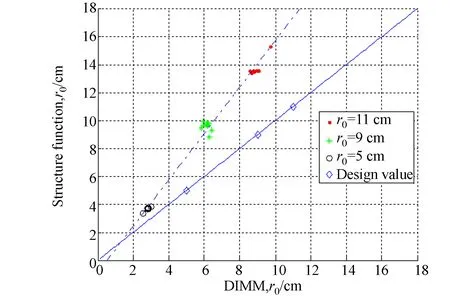
圖6　波前結(jié)構(gòu)函數(shù)法和DIMM法測(cè)量r0的結(jié)果比較Fig.6　Comparison of r0 measured by wavefront structure function and DIMM

2011年10-11月累計(jì)16個(gè)有效觀測(cè)夜晚，在長(zhǎng)春光機(jī)所自研的1.23 m自適應(yīng)望遠(yuǎn)鏡上分別使用波前結(jié)構(gòu)函數(shù)法和DIMM法測(cè)量大氣相干長(zhǎng)度，其結(jié)果對(duì)比如圖7所示。其中，曝光時(shí)間均為1.98 ms；累計(jì)8 000幀的平均值作為對(duì)比；DIMM法的單個(gè)r0的計(jì)算樣本數(shù)為200幀。圖7可看出，兩種方法測(cè)量結(jié)果的偏差均值為0.45 cm，標(biāo)準(zhǔn)差為1 cm，說(shuō)明兩種測(cè)量方法的結(jié)果在數(shù)值和偏差上相當(dāng)； 同時(shí)，隨時(shí)間變化，兩種測(cè)量結(jié)果在趨勢(shì)上趨于一致,這說(shuō)明在監(jiān)測(cè)整層大氣的r0上，波前結(jié)構(gòu)函數(shù)法同DIMM法的精度相當(dāng)。

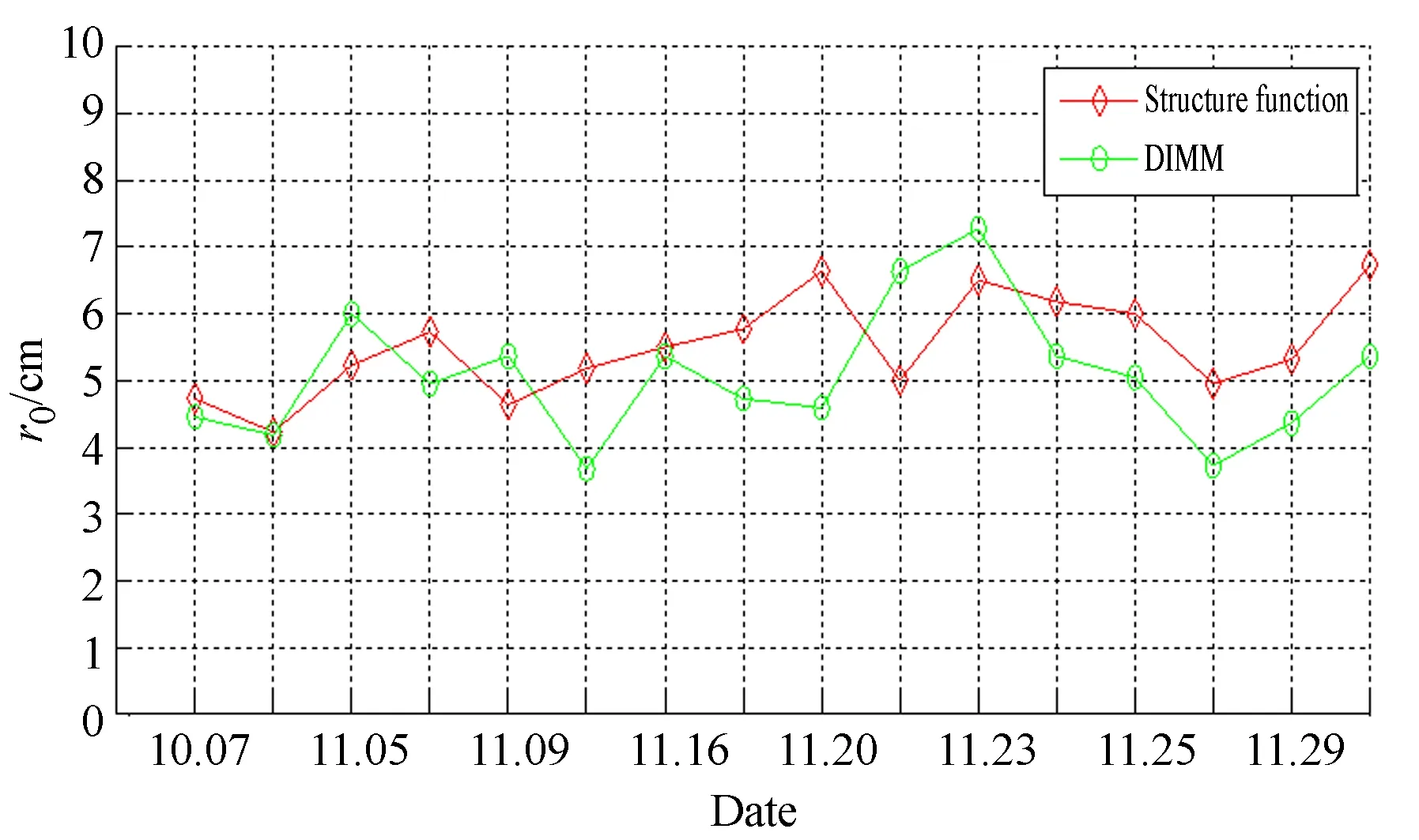
圖7　波前結(jié)構(gòu)函數(shù)法和DIMM外場(chǎng)測(cè)量r0的結(jié)果對(duì)比Fig.7　Comparison of r0 measured by wavefront structure function and DIMM in field

5　結(jié)　論

本文基于應(yīng)用波前結(jié)構(gòu)函數(shù)法，提出了一種瞬時(shí)測(cè)量大氣相干長(zhǎng)度的方法。實(shí)驗(yàn)結(jié)果表明：波前結(jié)構(gòu)函數(shù)法的測(cè)量精度同傳統(tǒng)的DIMM方法相當(dāng)，實(shí)測(cè)偏差小于0.43 cm(16個(gè)有效觀測(cè)夜晚)。波前結(jié)構(gòu)函數(shù)法能夠評(píng)價(jià)空間目標(biāo)受大氣影響的r0尺度大小，突破了DIMM方法只能測(cè)量恒星或行星的限制。此外，單幀短曝光測(cè)量可避免震動(dòng)對(duì)測(cè)量結(jié)果的影響。波前結(jié)構(gòu)函數(shù)法避免類(lèi)似DIMM方法空間采樣不足對(duì)測(cè)量結(jié)果的影響，拓展了視寧監(jiān)測(cè)設(shè)備的適用范圍，可用于地基大口徑望遠(yuǎn)鏡主鏡視寧度和自適應(yīng)光學(xué)系統(tǒng)內(nèi)部湍流的監(jiān)測(cè)。

[1]賈建祿，王建立，趙金宇，等.自適應(yīng)光學(xué)系統(tǒng)波前處理算法的優(yōu)化[J].光學(xué) 精密工程，2013,21(4):1026-1031.

JIA J L, WANG J L, ZHAO J Y,etal.. Optimization of adaptive optical wave-front algorithm[J].Opt.PrecisionEng., 2013, 21(4):1026-1031.(in Chinese)

[2]林旭東，劉欣悅，王建立,等. 137單元變形鏡的性能測(cè)試及校正能力實(shí)驗(yàn)[J].光學(xué) 精密工程，2013,21(2):267-273.

LIN X D, LIU X Y, WANG J L,etal.. Performance test and experiment of correction capability of 137-element deformable mirror[J].Opt.PrecisionEng., 2013,21(2):267-273.(in Chinese)

[3]于龍昆，吳毅，侯再紅，等.利用差分像運(yùn)動(dòng)監(jiān)測(cè)儀法測(cè)大氣相干長(zhǎng)度的研究[J].光學(xué)學(xué)報(bào)，2013,33(12):1201004-1-5.

YU L K, WU Y, HOU Z H,etal.. Study on the measurement of coherence length by differential image motion monitor[J].ActaOpticaSinica, 2013, 33(12):1201004-1-5.(in Chinese)

[4]DAVID L F. Differential angel of arrival: Theory, evaluation, and measurement feasibility[J].RadioScience, 1975, 10(1):71-76.

[5]MARC S, RODDIER F. The ESO differential image motion monitor[J].Astron.Astrophys, 1990,227:294-300.

[6]MARC S. ESO-VLT instrumentation for site evaluation in Northern Chile[J].SPIE,1986,628:138-141.

[7]饒瑞中，王世鵬，劉曉春，等. 湍流大氣中的激光束漂移的實(shí)驗(yàn)研究[J]. 中國(guó)激光，2000,27(11):1011-1015.

RAO R ZH, WANG SH P, LIU X CH,etal.. Experimental study of spot dancing of laser beam in turbulent atmosphere[J].ChineseJournalofLasers, 2000,27(11):1011-1015.(in Chinese)

[8]黃宏華，姚永幫，饒瑞中．四孔差分像運(yùn)動(dòng)測(cè)量大氣相干長(zhǎng)度的方法研究[J].強(qiáng)激光與粒子束，2007,19(3):357-360.

HUANG H H,YAO Y B, RAO R ZH. Measurement of atmospheric coherent length by four-aperture differential image motion method[J].HighPowerLaserandParticleBeams, 2007,19(3):357-360.(in Chinese)

[9]倪志波，黃宏華，黃印博，等. Dome效應(yīng)對(duì)四孔大氣相干長(zhǎng)度儀系統(tǒng)性能的影響[J]. 強(qiáng)激光與粒子束，2010,22(11):2551-2555.

NI ZH B, HUANG H H, HUANG Y B,etal.. Influence of Dome effect on system performance of four-aperture coherent length monitors[J].HighPowerLaserandParticleBeams, 2010,22(11):2551-2555.(in Chinese)

[10]陳浩，宣麗，胡立發(fā)，等. 大氣相干長(zhǎng)度的穩(wěn)定測(cè)量[J]. 光學(xué) 精密工程, 2013,21(4):911-918.

CHEN H, XUAN L, HU L F,etal..Steady measurement of atmospheric coherence length[J].Opt.PrecisionEng.,2013,21(4):911-918.(in Chinese)

[11]黃德權(quán)，周文超，邱紅，等. 哈特曼測(cè)量大氣相干長(zhǎng)度研究[J]. 強(qiáng)激光與粒子束，2014,26(8):081003-1-6.

HUANG D Q, ZHOU W CH, QIU H,etal.. Research on measurement of atmospheric coherence length using Shack-Hartmann wavefront sensor [J].HighPowerLaserandParticleBeams, 2014,26(8):081003-1-6.(in Chinese)

[12]耿則勛，陳波，王振國(guó)，等. 自適應(yīng)光學(xué)圖像復(fù)原理論與方法[M].北京：科學(xué)出版社，2010.

GENG Z X, CHEN B, WANG ZH G,etal..PerformanceAnalysisofAdaptiveOpticalSystemforSpatialObjectives[M]. Beijing: Science Press, 2010. (in Chinese)

[13]衛(wèi)沛鋒，盧振武，劉欣悅，等. 自適應(yīng)光學(xué)系統(tǒng)對(duì)空間運(yùn)動(dòng)目標(biāo)校正性能分析[J]. 光子學(xué)報(bào), 2015,44(7):0701001-1-7.

WEI P F, LU ZH W, LIU X Y,etal.. Performance analysis of adaptive optical system for spatial objectives[J].ActaPhotonicaSinica, 2015,44(7):0701001-1-7.(in Chinese)

[14]饒長(zhǎng)輝. 非Kolmogorov湍流情況下低階校正自適應(yīng)光學(xué)系統(tǒng)的性能研究[D]. 北京：中國(guó)科學(xué)院, 2000.

RAO CH H.PerformanceAnalysisofLow-orderCorrectionAdaptiveOpticalSystemforNon-KolmogorovTurbulence[D]. Beijing：Graduate University of the Chinese Academy of Sciences,2000.(in Chinese)

衛(wèi)沛鋒(1984-)，男，山西運(yùn)城人，博士研究生，助理研究員，2006年、2009年于西北工業(yè)大學(xué)分別獲得學(xué)士、碩士學(xué)位，主要從事自適應(yīng)光學(xué)、大氣光學(xué)的研究。E-mail:weipeifeng@gmail.com

林旭東(1982-)，男，福建莆田人，博士，副研究員，2005于長(zhǎng)春理工大學(xué)獲得學(xué)士學(xué)位，2010年于中科院長(zhǎng)春光機(jī)所獲得博士學(xué)位，主要從事自適應(yīng)波前校正技術(shù)方面的研究。E-mail:linxudong_82@126.com

(版權(quán)所有未經(jīng)許可不得轉(zhuǎn)載)

Simultaneous measurement of atmospheric coherence length

WEI Pei-feng1,2*, LIN Xu-dong1, WANG Liang1,WANG Ming-hao1

(1.ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun130033，China; 2.UniversityofChineseAcademyofSciences,Beijing100049，China)

When the differential image motion monitor method is used to measure the atmospheric coherence length, it needs a number of frames recorded with objective motions. Therefore, this paper proposes a simultaneous measuring method of the atmospheric coherence length based on the wavefront structure function for spatial objective. The method uses a Shack-Hartmann wavefront sensor to measure the Zernike coefficients of a frame of aberrated wavefront with short exposure. Then, it subtracts the initial aberration of optical system, removes the tip and tilt items and calculates the experimental structure function of aberrated wavefront. Finally, the simultaneous atmospheric coherence length is obtained by least-square approximation fitting with the theoretical structure function of aberrated wavefront satisfying the Kolmogorov turbulence theory. A test system is constructed by a turbulence phase plate and a number of experiments are conducted in an external field. The result shows that the measured atmospheric coherence length by using the proposed method based on the wavefront structure function matches well with that of the differential image motion monitor method. The ratio of mean value to standard deviation is less than 4.1% under different Greenwood frequencies and the mean difference of two methods is less than 0.45 cm in 16 effective nights. The method implements the simultaneous measurement of atmospheric coherence lengths of spatial objectives and also could be used to evaluate the seeing of observation sites, the atmospheric turbulence strength inside adaptive system and the mirror seeing of main mirror for a ground-based large aperture telescope.

adaptive optics; atmospheric coherence length; spatial objective; simultaneous measurement; wavefront structure function method

2015-11-13；

2016-01-07.

國(guó)家863高技術(shù)研究發(fā)展計(jì)劃資助項(xiàng)目(No. 2015AAXXX1003X)

1004-924X(2016)08-1840-06

P412.1

A

10.3788/OPE.20162408.1840