從問題入手,培養學生的數學思維能力
劉志美
從問題入手,培養學生的數學思維能力
劉志美

數學是思維的體操,問題是數學的心臟。培養學生的數學思維能力是數學教學的出發點,也是數學教學的落腳點。教師精心設問,激發學生的數學思維,引導學生解決數學問題是培養學生數學思維能力的關鍵。
一、貼近生活設問
數學教學設計的內容盡可能與生活實際相結合,接近學生已有的數學活動經驗,便能引發學生思考問題的積極性,培養數學思維能力。
例如,教一元二次方程的應用時,可設計這樣一道問題:某商店經銷一種銷售成本為每千克40元的水產品,根據市場分析,若按每千克50元銷售,一個月能售出500千克,銷售單價每漲1元,月銷售量就減少10千克,請解答下列幾個問題:
(1)當銷售單價為每千克55元時,計算月銷售量和月銷售利潤;
(2)設銷售單價為每千克x元,月銷售利潤為y元,求x與y之間的關系式;
(3)商店想在月銷售成本不超過10000元的情況下,使得月銷售利潤達到8000元,銷售單價應定為多少?
(4)要使月銷售利潤達到9000元,銷售單價應定為多少?
(5)有沒有可能獲得大于9000元的利潤?
這一組問題,貼近學生的生活,能促使學生運用所學知識解決問題,培養數學思維能力。
二、抓住知識聯系設問
有些數學知識聯系緊密,如表達形式、解題方法等都非常相似,學生容易混淆。如果在此設問,就能幫助學生辨別知識異同,牢固掌握知識。
例如,二次根式與平方根、算術平方根非常類似,學生往往分不清。對此,可設計如下問題:
(1)平方根、算術平方根及二次根式的聯系和區別是什么?,錯在哪里?
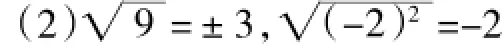
通過對這一組問題的解答,學生能輕松地把握平方根、算術平方根及二次根式的聯系與區別。
三、尋找解法中設問
解題教學在數學教學中占的分量很大,要提高學生的解題能力,就必須重視解題教學。在解題教學中,老師們喜歡一題多解,因為這樣能開闊學生的思維。但是我們不能僅停留在多種解法上,要善于設置問題,引導學生將不同的解法聯系起來思考,從而有效地培養數學思維能力。
例如,勾股定理的證明,學生是難以想到方法的,教師可以出示圖(甲)與圖(乙),讓學生證明兩個正方形的面積是否相等。因為兩個正方形的邊長都是a+b,所以它們的面積相等,即,所以a2+b2=c2。
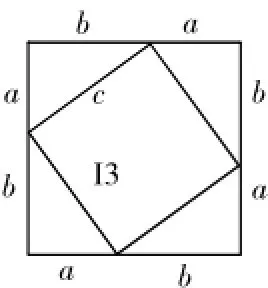
圖(甲)

圖(乙)
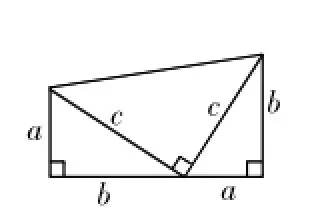
圖(丙)
在此基礎上,出示圖(丙),提出問題:如何運用圖(丙)證明勾股定理?
學生從上述兩種證法中可以發現,都是利用面積證明勾股定理。因為利用面積就容易湊出平方,與勾股定理聯系起來。
總之,在數學教學中,教師應具備很強的問題意識和創新意識,設計好數學問題,才能有效地培養學生的數學思維能力。
(作者單位:新邵縣教育局教研室)

