基于GM(1,1)-BP組合模型的車輛周轉器材需求量預測

何　健，王　亮，張大鵬，文正中

(1.軍事交通學院 研究生管理大隊，天津 300161； 2.軍事交通學院 軍用車輛系，天津 300161)

?

基于GM(1,1)-BP組合模型的車輛周轉器材需求量預測

何健1，王亮2，張大鵬2，文正中1

(1.軍事交通學院 研究生管理大隊，天津 300161； 2.軍事交通學院 軍用車輛系，天津 300161)

根據車輛周轉器材需求量的歷史數據特點，建立了GM(1,1)-BP組合模型。運用GM(1,1)模型，結合車輛周轉器材需求量的歷史數據對其進行預測，再針對預測中的殘差運用BP神經網絡進行適當修正。通過實例驗證，此組合模型優化了車輛周轉器材需求量的預測方法，彌補了單一預測模型的不足，提高了車輛周轉器材需求量預測的準確性。

車輛周轉器材；GM(1,1)模型；BP神經網絡；需求預測

車輛周轉器材中所涉及的器材品種繁多、對器材需求的影響因素十分復雜，這使得部隊車輛周轉器材需求量具有較大的時間波動性和隨機波動性。車輛周轉器材需求量與其影響因素既表現出線性關系又表現出非線性關系[1]，再加上單一的需求預測模型具有較大的局限性，因此，很難對其進行精確地預測。

本文重點研究的對象是車輛周轉器材中的不可修復器材，該種器材需求量大，具有一定的歷史數據；種類繁雜，關鍵性較低；受多項不可控因素影響，難以進行預測。針對該種器材需求的特性，提出了一種基于灰色模型(grey model,GM)和誤差反傳(back propagation,BP)神經網絡組合模型對車輛周轉器材的需求量進行預測的新方法。GM(1,1)模型需要的樣本數據少并且對線性關系預測精度高，而BP神經網絡具有良好的非線性動態特性和自適應能力，對其中的非線性關系能夠準確地進行預測[2]。因此，運用GM(1,1)-BP組合模型能夠有效克服各自模型中的不足，大大提高了預測精度，達到了相對最優的需求預測效果。

1　GM(1,1)模型的概述與構建

1.1GM(1,1)模型的概述

灰色預測法是指對原始數據進行挖掘和分析，找出其發展趨勢或隱含的規律，建立適當的灰色模型，并對整個系統的下一步狀態作出科學合理預測的方法[3]。GM(1,1)模型是灰色預測模型中運用最早最頻繁的模型。該模型包含了微分、差分和指數的相關性質，因此其性質是灰色的；模型中的參數變量是可以調整變化的，不是確定的，也是灰色的[4]。

1.2GM(1,1)模型的構建

1.2.1累加生成運算

累加生成運算在整個灰色預測模型構建中占著舉足輕重的位置，是模型構建的基礎。系統的灰量累積發展趨勢可以通過累加生成運算觀察出來，從而得到原始數據序列中所隱含的數學特性和變化規律[5]。假設原有非負歷史數據X(0)=(x(0)(1)，x(0)(2)，…，x(0)(n))，通過對X(0)累加得到一組新的數據序列X(1)=(x(1)(1)，x(1)(2)，…，x(1)(n))，其中

(1)

1.2.2微分方程的擬合

GM(1,1)的一階微分方程形式為

(2)

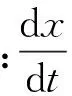
利用一次累加生成數列來擬合微分方程，即

(3)

由于式(3)中只含有一個變量x，a、b都為待確定的參數。因此，不妨設

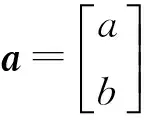
(4)

式中a是由a、b共同確定的參數向量。

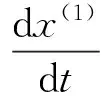
α(1)(x(1)(t+1))+aβ(1)(t+1)=b

(5)

式中：

α(1)(x(1)(t+1))=x(0)(t+1)

(6)

(7)

所以，根據式(5)、(6)和(7)，有

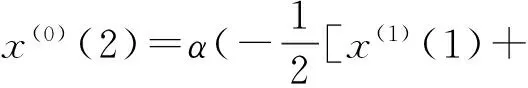
x(1)(2)])+b；

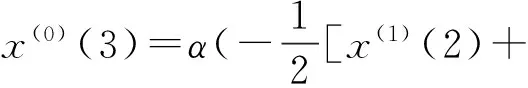
x(1)(3)])+b；

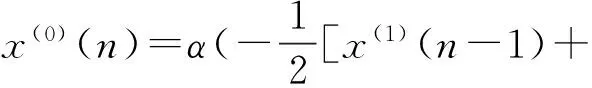
引入下列符號：

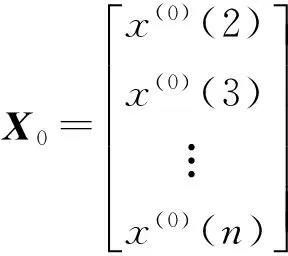
則有

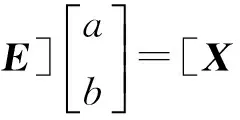
(8)

令B=[X|E]，即

則有X0=Ba，再依據最小二乘法，得

(9)

式中BT為矩陣B的轉置矩陣。

1.2.3預測方程的確定

通過積分的方法對上述擬合的一階微分方程進行求解，從而得出相應的時間函數為

(10)

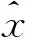
對上述時間響應函數進行復原，最終得出GM(1,1)模型的預測方程

(11)

1.2.4殘差序列的確定

檢驗GM(1,1)模型的預測精度，當其達不到相關要求時，可以通過引入殘差序列來改進已建立的預測模型，使其預測精度能夠有效提升。依據GM(1,1)模型的預測方程，可以得出殘差序列為

(12)

2　基于BP神經網絡對GM(1,1)模型的殘差修正

2.1BP神經網絡

2.1.1BP神經網絡的結構

BP神經網絡通常由輸入層、隱含層和輸出層3個層次組成，結構如圖1所示。

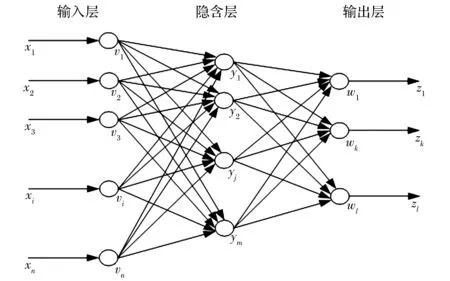
圖1　含有隱含層的BP神經網絡

BP神經網絡中，輸入向量X有n個元素，即X=(x1,x2,…，xi,…，xn)T；若隱含層輸出向量為Y，則Y=(y1,y2,…，yj,…，ym)T；輸出層輸入向量為Z，Z=(z1,z2,…，zk,…，zl)T。用矩陣V來表示從輸入層到隱含層所依次對應的權值向量集合，V=(v1,v2,…，vj,…，vn)T，其中vj表示在隱含層中第j個神經元所對應的權值向量大小；用矩陣W來表示從隱含層到輸入層所依次對應的權值向量集合，W=(w1,w2,…，wk,…，wl)T，其中wk表示在輸出層中第k個神經元所對應的權值向量大小[6]。

各層之間的數學關系為：

對于輸出層、隱含層分別有

(13)

(14)

式中傳輸函數f(x)均采用Sigmoid函數[7]：

(15)

2.1.2BP神經網絡算法的介紹

BP神經網絡算法的具體思想是：將數據樣本由輸入層開始輸入，經由隱含層進行相應的處理后再傳入輸出層。將輸出的數據與目標期望值進行對比，如果不符合相關要求，就進行誤差反傳。即將輸出值與期望值比較后所得的誤差通過隱含層再反饋給輸入層，同時在反饋的過程中每個神經單元都要分攤一定的誤差，修正改進各層神經單元權值的根據就是每個單元所對應分攤的誤差。整個正向傳入和誤差反傳的權值修正改進過程是循環往復的，直至最后輸出的誤差達到預期的要求為止[8]。具體算法流程如圖2所示。

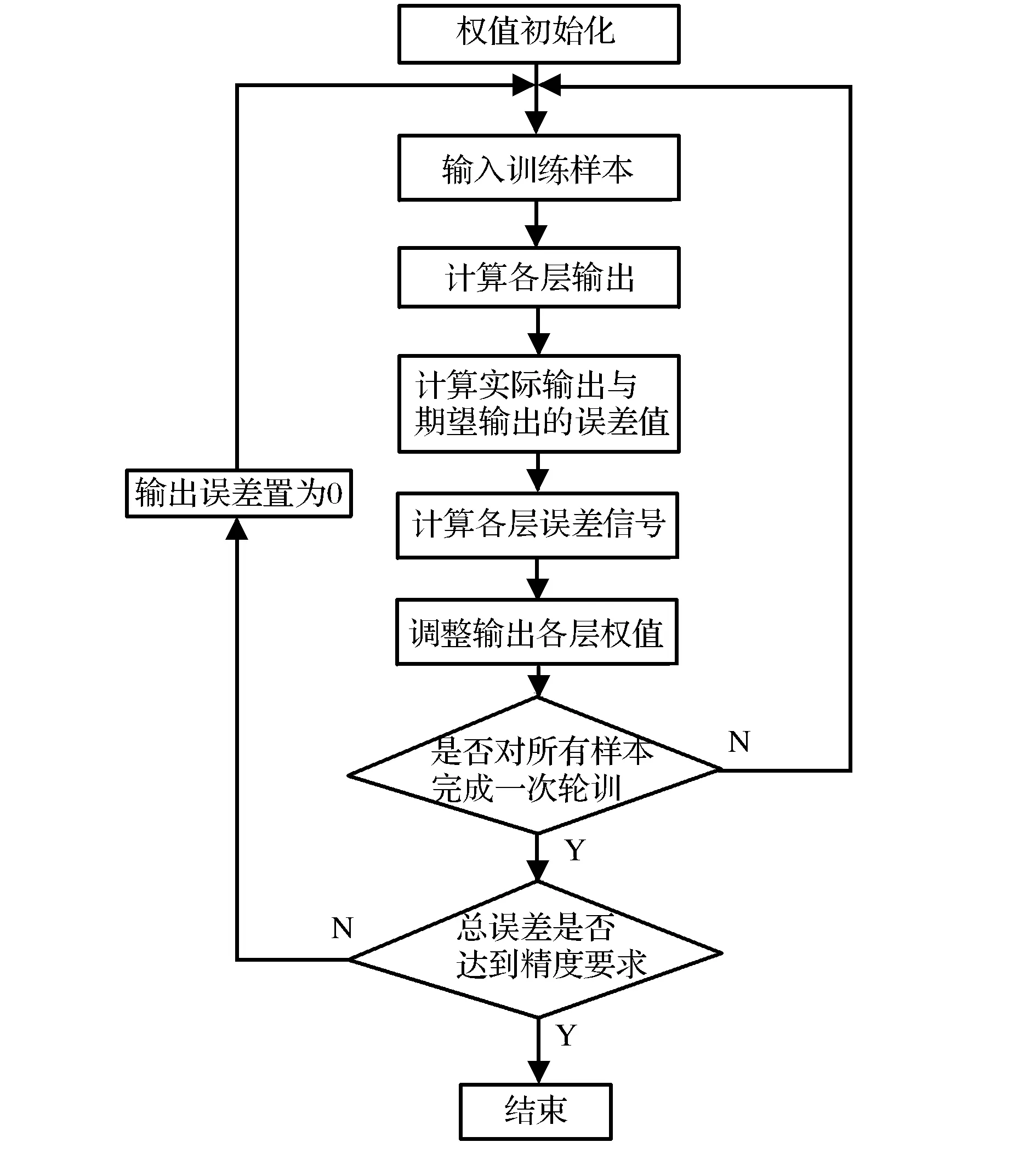
圖2　BP算法流程

2.2基于GM(1,1)-BP組合模型的構建

本文提出的GM(1,1)-BP組合模型，首先運用GM(1,1)模型對車輛周轉器材需求量進行初步預測，再運用BP神經網絡對GM(1,1)模型預測的殘差進行適當修正，這不僅研究挖掘出了影響車輛周轉器材需求量因素的非線性特征，而且也將線性特征考慮在內。最后將殘差修正結果與GM(1,1)模型預測結果進行合成，從而得到組合模型的車輛周轉器材需求量的最終預測值。組合模型的具體算法流程圖如圖3所示。

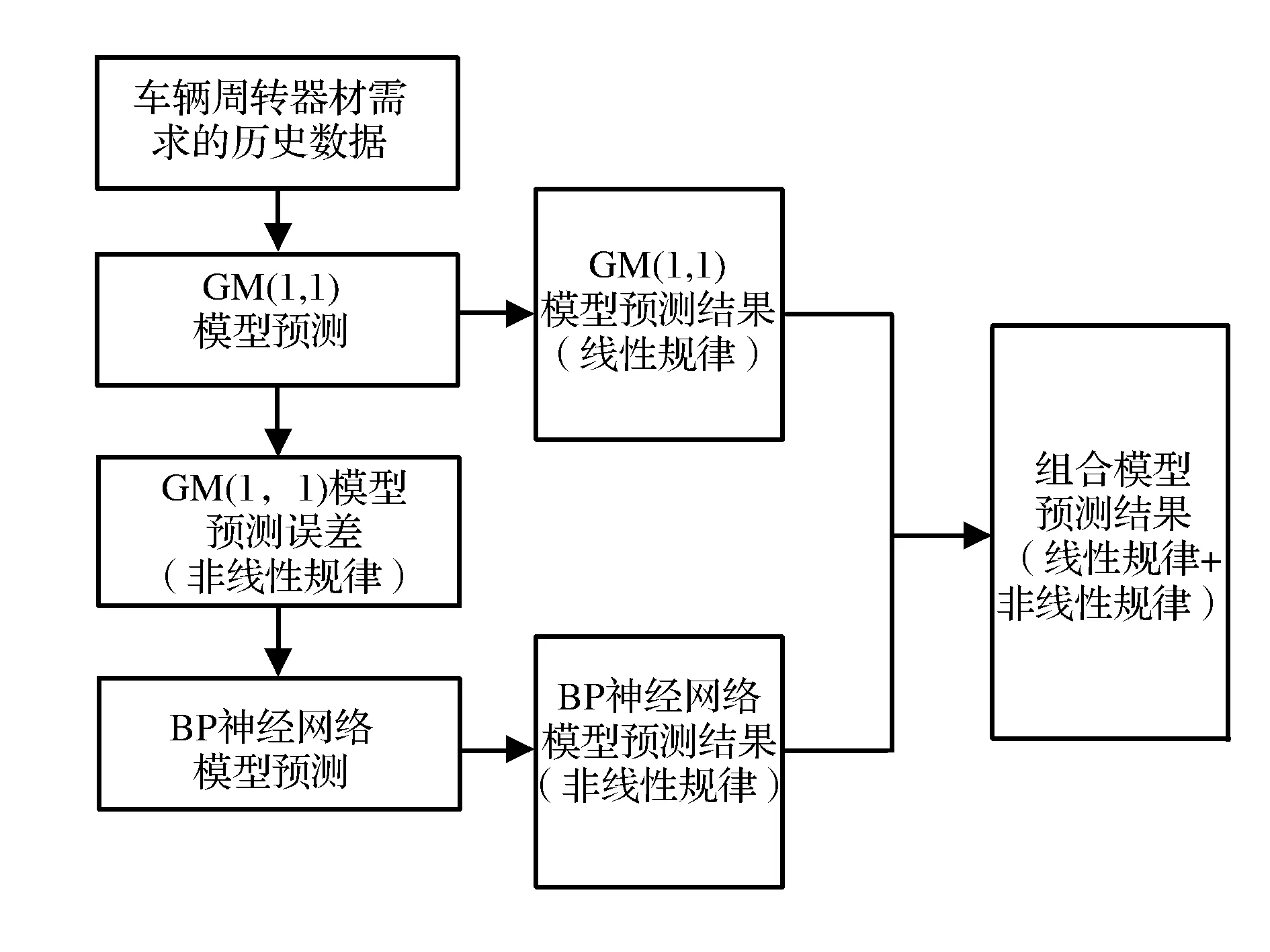
圖3　組合模型的算法流程

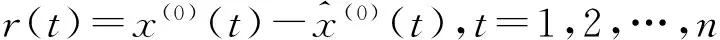
為方便計算，對需求量的殘差序列實行歸一化處理[9]，公式為

r′(t)=[r(t)-s]/(k-s)

(16)

(17)

式中r(t)max和r(t)min分別為需求量殘差序列中的最大值和最小值。

采用誤差的梯度下降算法對GM(1,1)模型的預測方程所輸出的殘差進行計算。最后運用仿真函數sim來對BP神經網絡進行仿真。具體調用形式為

z(t)=sim(net，r′(t))

(18)

式中：z(t)為網絡輸出；net為訓練對象；r′(t)為網絡輸入。

那么，由BP神經網絡修正調整好的殘差和GM(1,1)模型的預測值之和即為最終的車輛周轉器材需求量的預測值：

(19)

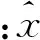
對于本文所研究的車輛周轉器材需求量預測，每次訓練所輸入與輸出的殘差僅有一個，即輸入層與輸出層所包含的神經元數量m、n均為1。隱含層所包含的神經元數量l取值可以依據下式得出[10]：

(20)

式中，q取[0，10]，為常數，計算精度和運算次數會跟著q取值的增加而增加。

3　GM(1,1)-BP組合模型的可靠性檢驗

根據系統可靠性理論對GM(1,1)-BP組合模型的可靠性進行相關檢驗[11]。具體方法如下：

根據殘差的表達式可以得到殘差均值為

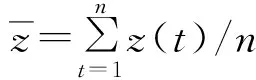
(21)

則殘差的方差為

(22)

原始數據的方差為

(23)

驗差比值(標準差比)為

C=S1/S2

(24)

組合模型的小誤差概率為

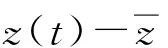
(25)

根據P與C的大小，來確定組合模型的可靠性等級，具體關系見表1。

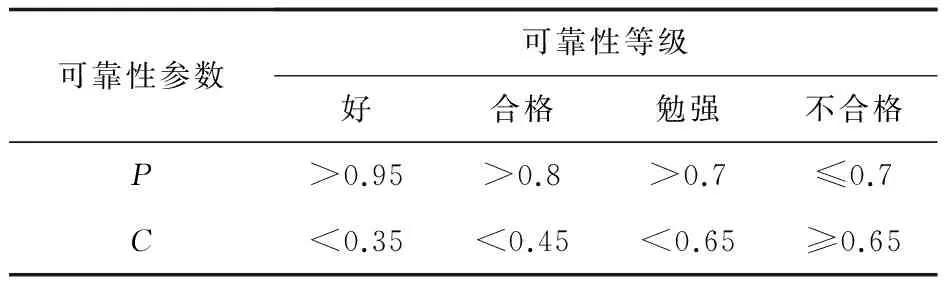
表1　P、C值與可靠性等級的關系

4　實例驗證

本文結合對XX戰區直屬器材倉庫的實地調研和數據收集，以該單位的主力運輸車XXX的雨刮器為研究對象，搜集其自2001年配備列裝部隊以來10年的需求數據，將其作為數據樣本，首先運用GM(1,1)模型對其需求量實行相關預測。再選取第11年至第14年的實際需求量和其對應的預測值進行對比，具體結果如圖4所示。

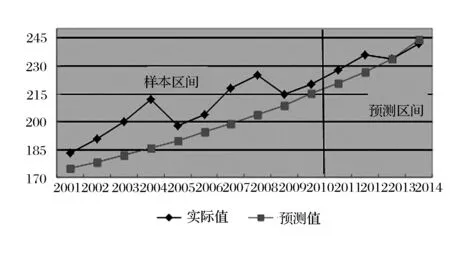
圖4　XXX運輸車雨刮器需求量實際值與預測值對比

由圖4可知，需求樣本的離散程度比較大，該車型的雨刮器需求量隨機性和波動性比較強。單單運用GM(1,1)模型預測出的數據大致呈現線性規律，與實際需求量偏差較大。因此，需要運用BP神經網絡對GM(1,1)模型預測中的殘差序列進行修正改進，再與初步預測值實行累加處理，得出GM(1,1)-BP組合模型的最終預測結果(如圖5所示)。

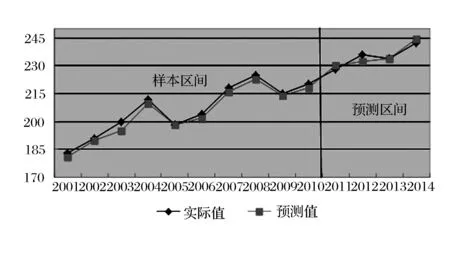
圖5　修正后的XXX運輸車雨刮器需求量實際值與預測值對比

由圖5可以直觀地反映出，經過BP神經網絡的修正，大大降低了預測的誤差，有效提高了預測的相關精度。因此，GM(1,1)-BP組合模型的預測效果要明顯好于單一的GM(1,1)預測模型，能夠很好地提升車輛周轉器材需求量的預測精度。

根據第三部分的可靠性檢驗相關內容對GM(1,1)-BP組合模型的可靠性進行檢驗分析，具體結果見表2。

表2　可靠性檢驗結果

5　結　語

通過構建GM(1,1)-BP組合模型，利用BP神經網絡的非線性動態特性和魯棒性強的特點對GM(1,1)模型中的殘差序列進行修正，有效規避了單一預測模型的缺陷。這既考慮了車輛周轉器材需求量影響因素中的非線性特征，又考慮了線性特征，使車輛周轉器材的需求量預測達到了較高精度，為部隊車輛周轉器材的需求量預測提供參考。

[1]王亮.軍用車輛器材保障概論[M].北京:金盾出版社,2014：27-59.

[2]劉傳波.軍用車輛保養器材消耗規律研究[D].天津:軍事交通學院,2007：37-41.

[3]胡曉華,吉承儒,虞敏.灰色預測法的進一步推廣及應用[J].大學數學,2013(1):117-121.

[4]劉思峰,曾波,劉解放.GM(1,1)模型的幾種基本形式及其適用范圍研究[J].系統工程與電子技術,2014(3):501-508.

[5]杭力,韓直,杜益文.BP神經網絡和GM(1,1)灰色模型在公路客運量預測中的應用[J].公路交通技術,2006,4(2):110-113.

[6]趙成柏,毛春梅.基于ARIMA和BP神經網絡組合模型的我國碳排放強度預測[J].長江流域資源與環境,2012,21(6): 665-672.

[7]童飛.基于BP神經網絡的水上交通事故預測及MATLAB實現[D].武漢:武漢理工大學,2005：37-39.

[8]DONG Yu， YANG Qiang, YAN Wenjun. Short-term electricity price forecasting based on MPSO-BP algorithm[J]. Advanced Materials Research, 2012, 388:1351-1355.

[9]聶小沅,李德建.基于BP神經網絡與GM(1,1)模型組合算法的橋梁耐久性預測[J].鐵道科學與工程學報,2015,12(4): 839-845.

[10]張俊深,袁程煒.基于BP神經網絡與修正GM(1,1)模型的能源消費組合預測[J].統計與決策,2016,5(24):90-93.

[11]郎茂祥.預測理論與方法[M].北京:清華大學出版社,2011：184-187.

(編輯：孫協勝)

Vehicle Turnover Equipment Demand Prediction Based on GM(1,1)-BP Combined Model

HE Jian1, WANG Liang2，ZHANG Dapeng2, WEN Zhengzhong1

(1.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China; 2.Military Vehicle Department, Military Transportation University, Tianjin 300161, China)

A combined algorithm based on GM(1,1)model and BP neural network is constructed according to the data collected about the demand for vehicle turnover equipment. The vehicle turnover equipment demand is predicted by using GM(1,1)model and is then modified by using BP neural network. The case study shows that this model optimizes the method of predicting, makes up for the deficiency of single predicting model and improves the accuracy of the prediction.

vehicle turnover equipment; GM(1,1)model; BP neural network; demand prediction

2016-04-05；

2016-05-05.

何健(1991—)，男，碩士研究生；

王亮(1964—)，男，教授，碩士研究生導師.

10.16807/j.cnki.12-1372/e.2016.08.009

E246

A

1674-2192(2016)08- 0037- 05