多方免密鑰協商加密計算探究
楊賓(四川大學計算機學院,成都 610065)
多方免密鑰協商加密計算探究
楊賓
(四川大學計算機學院,成都610065)
0 引言
云計算是一種全新的在線計算模式,它是基于互聯網服務相關的使用和交付模式。根據美國國家標準與技術研究院(NIST)定義:云計算是一種按使用量付費的模式,這種模式提供可用的、便捷的、按需的網絡訪問,進入可配置的計算資源共享池(資源包括網絡、服務器、存儲、應用軟件、服務),這些資源能夠被快速提供,只需投入很少的管理工作,或與服務供應商進行很少的交互。云計算為企業和個人帶來了福音,用戶不再需要自己搭建服務平臺,只需要向云服務提供商按需購買相應的服務(存儲、計算資源),只用很少的費用就能得到巨大的計算能力。云服務減少了用戶的系統管理、維護成本,并且避免了安全風險,收益大。云計算模式引起了商業領域、企業經營的大變革。
雖然云計算服務發展迅速,但云端的用戶隱私數據一直令人擔憂。云服務提供商的面前,用戶一直出于弱勢地位。雖然服務商一在承諾會保護數據隱私,但是并不能排除黑客攻擊或者內部管理人員為了一己私利販賣數據庫的用戶數據。大量企業不敢將自己的數據存儲到云端,擔心服務商有意無意的使用自己的企業數據,泄漏商業秘密。數據泄漏已經嚴重阻礙到云計算服務的使用。一般的數據保護方式是采用數據加密,將數據庫的數據加密存儲。如果數據庫被拷貝,沒有密鑰,數據也不會被解密泄漏,但是會增加數據操作復雜性:
①每一次操作之前,需要解密數據:m=D(c);
②操作數據:m'=F(m);
③操作完成之后,必須再一次加密數據:c'=E (m')。
安全永遠和效率是負相關,追求數據安全性,必將導致數據處理效率降低。每一次操作都將進行一次數據加密,處理時間將會嚴重浪費在加解密算法里面,真正用于數據處理的CPU時間將會變少。另一個問題是密鑰存儲問題,密鑰必須交給服務提供商,他們可以自行決定是否對加密數據解密,“監守自盜”的可能性并沒有被排除。直接在密文上面進行數據處理的同態加密應運而生。
1 同態加密
同態加密的定義可以描述為對于明文數據m1,m2加密,可以在它們對應的密文之上進行如下操作⊙。操作的結果解密之后,同直接對明文的操作值一樣。
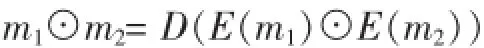
1.1同態加密的發展
同態加密的概念的首次提出是1978年,Rivest,Adleman,Dertouzos在文獻[1]中為了解決明文的泄露問題,采用的一種同時具有加法同態和乘法同態的算法。但是該方案和隨后的改進方案都不能有效克制密文膨脹,導致復雜度升高,效率和安全性較低,不能抗已知明文攻擊。之后全同態加密成為了密碼學一個研究熱點,一個開放的難題。直到2009年,由Gentry在文獻[2]構造了第一個在格上的完備理論的全同態加密方案。通過“稀疏子集和”問題的假設,從而在進行各種密文操作的之后依靠自己的解密函數進行同態解密,降低了密文噪聲的增長,最終在這種假設下獲得全同態加密的理論基礎。Gentry為全同態加密開啟了一扇大門,根據他的理論產生了多種改進方案[3-4]。但是由于同態解密無論怎么改進,效率依然十分低下,產生了基于LWE和RLWE的問題的同態加密方案[5-8],不再需要進行同態解密技術,使用密鑰交換技術和模交換技術就能很好地控制密文的維數增長和密文的噪聲增長。
1.2NTRU 同態加密
NTRU最先由Jeffrey,Jill等人提出的一種公鑰加密[9]。它的困難問題是在格中尋找最短向量(SVP)的數學難題。格是一組在Rm中n個線性無關向量的整系數集合。表示為:
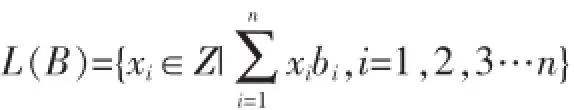
其中b1,b2,b3…bn是在Rn空間中一組線性無關向量,它們共同構成了格L的一組基。格可以有不同的基表示,一個格的基并不唯一。
最短向量問題[10]:B∈Zn×m是格L的一組基,在格L (B)中的尋找一個非零向量Bx,使得||Bx||≤||By||,對任意的向量y∈Zm均成立。
NTRU是構建在環上,通過多項式在環上進行各類操作。它只涉及了簡單的模乘法運算和模求逆運算,沒有大數因式分解和離散對數等大量運算,所以NTRU的效率更高,加、解密運算速度顯著。它的困難問題又是格上最短向量問題,在維數較大的格里,具有抗量子計算能力。另外在全同態技術還不具有實用意義的時候,NTRU作為部分同態加密方案(somewhat
homomorphic encryption or partially homomorphic en-cryption),針對加法乘法的同態操作有天然優勢。
1.3安全多方計算
安全多方計算(SMC)是一種協同計算模式,希望在各個互不信任的參與方共同參加一種計算,但是不會把自己的輸入泄露給其他參與者。每個參與者將輸入數據提交給可信的第三方進行計算,計算完成之后,將結果返回給所有參與者,但是參與共同計算的時候不止要對其他參與者保密,同時也要對第三方計算平臺保密。因為現實里,并沒有完全可信的第三方。多方計算的SMC模型由以下四個方面組成:參與方、安全性定義、通信網模型、信息論安全與密碼學安全。
為了保護在云端的數據安全,不希望透露給任何人,包括參與者和第三方云服務商。所有存放在云端的數據采用同態加密,云服務商只能對密文進行計算。參與方產生自己的密鑰,將自己的數據進行加密之后,交給第三方進行計算。計算完畢之后,得到結果。在公鑰加密體制內,參與方在加密之前需要進行密鑰協商,密鑰協商會導致一系列問題。(1)密鑰協商需要花費額外的時間。(2)在互聯網上海量的參與者進行密鑰協商會增加許多不確定的因素。針對以上問題,本文提出了多方免協商加密計算,來破除密鑰協商增加的時間復雜度。
2 多方免協商加密計算
通過NTRU的同態特性將云端數據加密之后進行有效的計算,利用經典的SHA-1哈希算法對參與方生成自己的數據計算哈希值,使得密文具有自己的獨立特性。對明文數據進行雙重加密,一層是NTRU,保護數據的安全性和同態性。另外一層是哈希算法,增加數據的身份特性,這樣對參與計算的用戶,擁有獨立的解密權,沒有參與的用戶無法解密結果。
2.1數據解密過程
典型的NTRU方案參考文獻[11],NTRU是構建在商環Ζ[χ]/(χN-1)。公鑰是Η=αFa*Β(mod β),私鑰Α∈Lf,Β∈Lg,Lf,Lg是整系數多項式。N,α,β取整數,β為2的冪次方且β>>α。
①密鑰生成:隨機任意選擇3個多項式A,B和D,A和 B分別關于 mod α,mod β的可逆多項式 Fα,Fβ,D∈Lg。
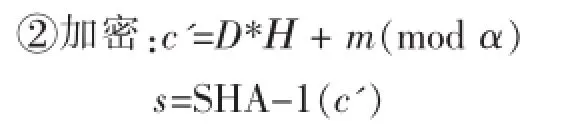
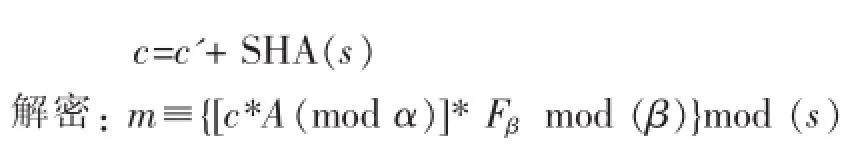
2.2多方計算過程
每一個參與方必須使用一樣的加密和解密策略來處理數據。加密之后將
①暫時抹去身份痕跡:c1=c1-s1;c2=c2-s2
②計算數據:c3=c1⊙c2(⊙在NTRU加密方案中可以為加法同態或者乘法同態),s3=s1*s2,c3=c3+s3
③返回結果:
上例中只有參與者有查看的權利,其他任何人都不能正確地解密結果,包括云計算提供商。
2.3正確性證明我們分別以加法同態和乘法同態進行驗證。(1)加法同態性證明


3 結語
多方免密鑰協商加密計算能夠將完全將輸入和輸出加密。輸入只有一個參與方能夠正確解密,所有參與方可以解密輸出。通過哈希函數為每一個參與方設置身份標識,身份標識不需要和其他參與方進行協商,加密過程的時候,為每一個加密數據保留自己身份痕跡。只要輸出存在自己的身份痕跡,參與方就能正確解密數據。本文的加密安全性來自于格的SVP問題,能夠對抗量子計算。云計算方只能按部就班進行同態運算,完全不了解參與運算的數據和運算結果,保護了存放在云端的隱私數據。同時參與方之間根本不知道對方的輸入值,達到了安全多方計算的根本要求。但是本方案存在一些不足之處,1)SHA-1最大的抗沖突性為280,如果在大量的參與方存在的情況下,由于生日悖論存在,攻擊者的哈希值猜測的哈希沖突會得到很大的提升,使得沒有查看計算結果的攻擊者,有機會查看計算結果。2)哈希函數的增加會導致一定的數據膨脹。
[1]Rivest R,Adleman L,Dertouzos M.On Data Banks and Privacy Homomorphisms[M].[S.l.]:Academic Press,1978:169-177.
[2]GENTRY C.Fully Homomorphic Encryption Using Ideal Lattices[C].ACM,2009:169-178.
[3]van Dijk M,Gentry C,Halevi S,et al.Fully Homomorphic Encryption over the Integers[C].Proc.of Cryptology-CRYPTO'11.[S.l.]: Springer-Verlag,2011:24-43.
[4]Gentry C,Halevi S.Fully Homomorphic Encryption Without Squashing Using Depth-3 Arithmetic Circuits[C].Proc.of FOCSIEEE'11. [S.l.]:Springer-Verlag,2011.
[5]ZvikaBrakerski and Viod Vaikuntanathan.Efficient Fully Homoorphic Encryption from(Standard)lwe.In 2011 52nd Annual IEEE Symposium on Foundations of Computer Science,2011:97-106
[6]Vadim Lyubashevsky,Chris Peikert,Oded Regev.On Ideal Lattices and Learning with Errors Over Rigns.In EUROCRYPT-2010,volume 6110 of LNCS,2010:1-20
[7]Zvika Brakerski,Craig Gentry,Vinod Vaikuntanathan.Fully Homomorphic Encryption without Bootstrapping[C].ACM Transactions on Computation Theory,2014.7:[13:1]-[13:36]
[8]Ruan de Clercq,Sujoy Sinha Roy,Frederik Vercauteren.Efficient Software Implementation of Ring-LWE Encryption[C].EDA Consortium,2015.3:339-344
[9]J.Hoffstein,J.Pipher,J.H.Silverman.NTRU:A Ring-Based Public Key Cryptosystem[C].In:Algorithmic Number Theory(ANTS-III),LNCS 1423,Berlin:Springer-Verlag,June 1998:267-288.
[10]Goldreich o,Goldwasser S,Halevi S.Collision-Free Hashing from Lattice Problems[C].Electronic Colloquium on ComputationalComplexity(ECCC),1996,3(42):236-241
[11]胡予濮.一個新型的NTRU類數字簽名方案[J].計算機學報,2008,31(9):1661-1666.
Cloud Security;Secure Multi Party Computation;Homomorphic Encryption;NTRU
Research on Encryption Computation of Multi-Party Free-Key Negotiation
YANG Bin
(College of Computer Science,Sichuan University,Chengdu 610065)
1007-1423(2016)07-0012-04
10.3969/j.issn.1007-1423.2016.07.003
楊賓(1989-),男,四川浦江人,碩士研究生,研究方向為信息安全
2016-01-21
2016-02-21
為了保護在云端的隱私數據,改變用戶的弱勢地位,安全多方計算得到廣泛關注。而安全多方計算是需要各方提前進行密鑰協商,增加整個多方計算的復雜度和不安全因素。為了解決上述問題,設計一種基于NTRU同態加密的多方免協商計算模型,縮短整個計算的步驟,降低風險。保護隱私數據和計算結果不被云服務商泄露,同時也不會被沒有參與過計算的用戶知曉計算結果。
云安全;安全多方計算;同態加密;NTRU
In order to protect the privacy of data in the cloud,to change the user's weak position,secure multi-party computation has been widely concerned.Secure multi-party computation is required for all parties for key agreement in advance,which increases the complexity and the unsafe factors of the whole multi-party computation.In order to solve the above problems,designs a method based on NTRU,which is based on the computation model of multi-party free-key negotiation,which shortens the calculation steps and reduces the risk.Privacy preserving data and computing results are not revealed by the cloud service provider,at the same time the user who not be involved in calculating not known results.

