基于粗糙集神經網絡的科技金融信用風險評價研究

王潔，陳剛

（1.東莞市電子計算中心，東莞 523123；2.廣東理工職業學院計算機系，中山 528458）

基于粗糙集神經網絡的科技金融信用風險評價研究

王潔1，陳剛2

（1.東莞市電子計算中心，東莞 523123；2.廣東理工職業學院計算機系，中山 528458）

針對科技金融信用風險評價的效率低下，導致信貸審批成本過高，歸其原因為科技金融服務行業針對企業信用評價模型不佳，評價指標過多，評價時間過長，導致成本過高；針對此不足，提出一種基于粗集神經網絡的科技金融信用風險評價模型，該模型在不影響分類屬性的原則下有效地約簡企業的財務指標，同時利用BP神經網絡容錯能力，對信貸企業進行很好的分類，最后將該模型應用于實驗，實驗表明該模型有效。

科技金融；風險評價；粗糙集；神經網絡

0 引言

科技和金融緊密結合是金融服務實體經濟、助推經濟轉型升級的有效途徑，是貫徹落實創新驅動發展戰略的有效支撐措施。近年來隨著經濟不斷發展，科技與金融結合也越來越活躍，而在科技金融中信用貸款業務也不斷增加，然而，信貸效率卻非常低，其主要原因是信貸審批手續過于煩瑣，調查信貸指標過多，導致審批成本上升和審批周期過長，這些現象與活躍的信貸市場形成鮮明的對比，也困擾著大量的科技金融機構，特別對于政府性區科技金融服務機構，它們每天面臨大量本地區企業信用風險評估，這些評估活動表現為量大、指標多、時間長，嚴重地阻礙了當地經濟的快速發展。

國內已經有很多學者做了這方面研究，在科技金融信用評價方面的研究不多，如盧超等人提出商業銀行對中小企業信用風險評價的方法探索，但該文僅僅從方法上對普通企業信用評價給出了指導［1］；樓際通等人提出的商業銀行個人信用風險評價的投影尋蹤建模及其實證研究，是以數學建模為工具，從而可以對信用進行分類和量化，但問題是當指標數據太大時，顯然要耗費大量的時間［2］；曾詩鴻等人提出了基于KVM模型的制造業上市公司信用風險評價研究，該模型雖然針對性很強，但對于科技型的企業則有些乏力［3］；這些大部分都是從普通企業指標去研究的，但是針對科技型企業研究的極少，如汪泉等提出的科技金融信用風險的識別、度量與控制［4］，雖然比較詳細了描述了科技金融中的企業信用評價與度量應該關注因素，同時提到一個“SPECAIL”信用評價法，但是該方法信用評價的時間過長，浪費金融服務行業機構的時間更加大了科技型企業的風險，因為科技型企業的彈性較大，在缺少資金情況下，倒閉的風險比普通企業更大，當然該類型的企業也可以在較短的時間內贏利，因此該類企業對時間的控制顯得非常重要。

基于上述情況，針對于科技金融中信用風險評估過慢、準確率不高；同時科技型企業的償債能力的彈性大等特點，本文提出了一種基于粗集神經網絡的科技金融信用風險評價模型，該模型利用粗糙集的約簡功能可以刪除冗余數據，減少了BP神經網絡的輸入維，從而減少了指標數據的采集時間和減輕了工作量，更減少了BP神經網絡的訓練時間和分類時間，提高了科技金融服務行業信貸審批工作效率，節省了科技金融服務審批成本和科技型企業的信貸成本，為科技金融服務工作的順利展開創造了一定的技術條件；同時由于科技型企業的償債能力彈性大，快速獲得貸款能為科技型企業的生存創造一定的條件。

1 相關理論

科技金融是以促進科技創新活動為目的，以組織運用金融資本和社會資本投入科技型企業為核心，以定向性、融資性、市場性和商業可持續性為特點的金融活動總稱。

科技金融服務主要解決科技型企業貸款難，融資難的問題，引進銀行、創投、擔保、小額貸款、投資管理、資產評估、知識產權質押等金融和服務機構，整合與集成各相關服務功能，為企業提供促成技術交易一攬子解決方案。業務包括創業企業投資服務、企業貸款擔保服務、企業投融資策劃服務、小額貸款服務、企業投融資服務、下崗失業小額貸款擔保、私募股權投資、大學生自主創業貸款擔保、企業銀行貸款擔保、無抵押貸款（擔保）等。因此，科技金融服務的核心是科技型企業的信用風險評估。

本文的模型是基于粗糙集和BP的神經網絡網絡的組合模型，在該模型中涉及到粗糙集與BP神經網絡，粗糙集理論在當今的人工智能智能領域有著廣泛的應用領域。本文應用了粗糙集理論在不減少依賴度的前提下對企業的冗余指標進行刪除，從而減少了財務指標的采集時間，減少了BP神經網絡的輸入維，減少BP神經網絡的訓練時間和分類時間，進一步縮短了信貸系統的審批時間，節約了信貸審批成本；應用BP神經網絡進行分類是因為BP網絡具有較好的泛化能力和容錯能力，同時利用粗糙集可以約簡輸入維，提高BP網絡的收斂時間。

2 粗糙集的相關理論

粗糙集是由波蘭科學家Z.Pawlak于1982年提出來的。粗糙集理論是繼概率論、模糊集、證據理論之后又一個處理不確定性的數學工具。作為一種嶄新的軟計算方法，粗糙集近幾年來越來越受到重視，其有效性已在金融工程、智能控制、模式識別等眾多領域得到了證實，也是當今人工智能領域中的研究熱點之一。同時，其在處理噪聲、不確定性甚至不完整性方面也有著卓越的優勢［5-7］。

（1）上近似和下近似概念 理解上近似于下近似，首先要定義知識庫，令知識庫K=（U，S），U，S分別表示論域及在論域上的一個等價關系簇，對于X，若?x?U以及論域U上的一個等價關系R∈IND（K），則認為R的上近似與下近似分別表示為（1）（2）。

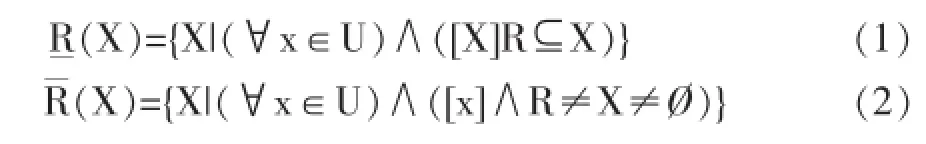
同時用bnR=R（X）-R（X）表示X對于R的邊界域，定義posR（X）=R為X等價關系R的正域。定義negR（X）=U-R（X）為X對R的負域。則R=posR（X）∪bnRR（X）。

（2）知識的約簡 約簡是粗糙集理論應用的重要方面之一。粗糙集約簡認為，屬性對知識庫的決策的重要程度應該不相同，有些數據甚至冗余，知識約簡正是通過尋找其屬性的最小依賴集，從決策表中剔除一些對決策基本沒有作用的屬性的過程，簡稱為約簡。

同時若知識庫中存在一個這樣的等價關系R=｛P，Q｝，則認為P∩Q是等價關系上的一個不可分割的等價關系，則記IND（R），此時Q的P上近似記為：

對于給定的知識庫K=（U，S）和知識庫上的一組關系P?S，對于任意的G?P，若G滿足以下條件：

①G是獨立的，

②IND（G）=IND（P）。則稱G為P的一個約簡，表示為G∈RED（P），認為RED（P）為P的全體約簡組成的集合。

（3）知識的依賴度 已知某知識庫K，若存在P且?P，Q∈IND（K），則知識依賴度的定義為公式為：

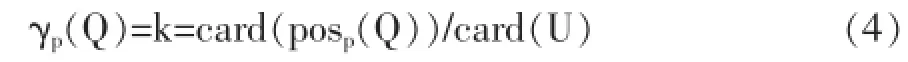
其中γp（Q）表示知識Q對P依賴程度，Card表示集合運行中的基數運算符，若γp（Q）為1，則認為Q完全依賴于P；若γp（Q）介于（0，1）時，則認為Q部分依賴于P，且Q中有部分是由P導出的；若γp（Q）為0，則認為Q與P完全沒有關系，表示P的任何變化都對Q無影響。

（4）知識的重要度 知識重要度是表示某個知識庫中某個屬性對于整個知識系統的重要程度的一個維度，對于知識系統中的所有屬性，若去除一些屬性之后，若論域U的劃分還和以前一樣，則認為該除去的屬性對于知識系統來說不重要，若除去一些屬性之后，論域U的劃分和去除屬性前不一樣，則認為該去除的屬性對知識比較重要，若知識系統IS=｛U，Q，V，f｝且?P?Q，以及α∈P，則知識系統中表示重要度的公司如下：

由公式（5）可以知，若是Sig越大，則說明α屬性對于C的劃分的影響越大，α屬性對于知識系統的重要度就越大；若Sig=0，則說明α屬性對C的劃分沒有影響，可以認為α屬性對IS重要度較低。

3 神經網絡理論

本文中的神經網絡主要是是BP（Back Propagation）神經網絡，BP是由Rumelhart和McCelland科學家于1986年提出的，是一種按誤差逆向傳播的算法訓練的多層前饋式網絡，是當今神經網絡應用領域最廣泛的網絡模型之一［8］。BP神經網絡能夠自動學習和存儲大量的模式映射，并且不需要事先準備描述的數學公式，就能以最速的速度進行學習，并且通過不斷地調整權值和閾值來達到網絡訓練的要求，該神經網絡模型的拓撲結構包括輸入層、隱含層、輸出層，如圖2所示。

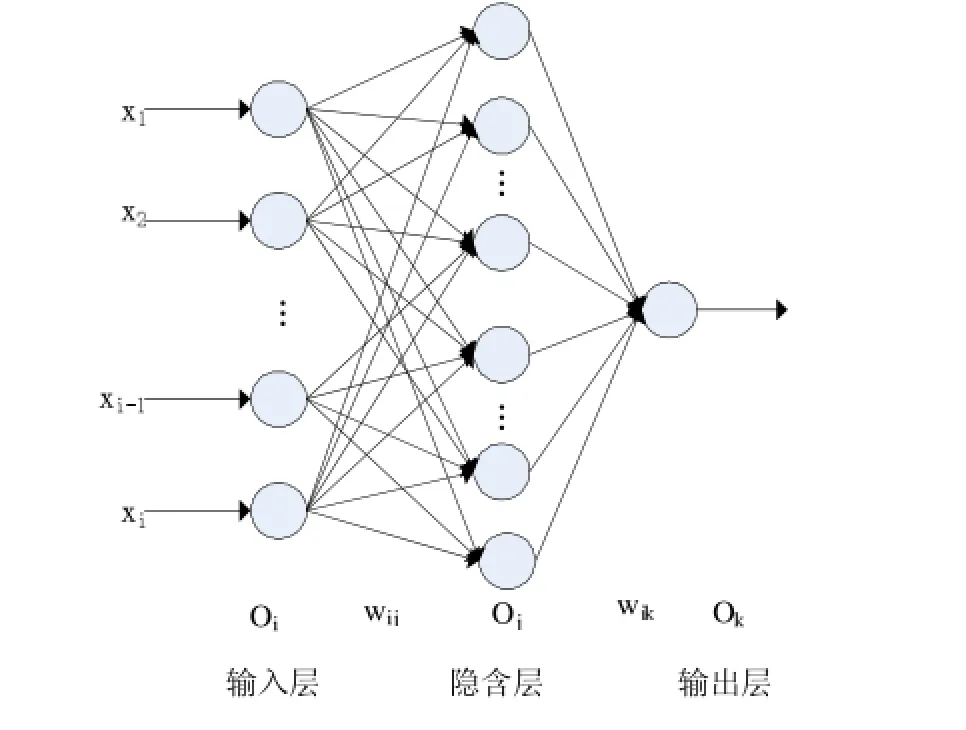
圖2 三層前饋式神經網絡模型

在BP神經網絡中，令I代表輸入，O代表輸出，對于輸入層的神經元i，它它的輸入等于輸出，即Ii=Oi，對于隱含層的神經元j，則其輸入為線性組合，如公式：

其中ωij代表輸入層i節點到隱含層j節點之間的權中，茲表示偏置，并且用S型函數做隱含層神經元j激活函數f（x），f'（x）為f（x）的導函數，同時令f（x）即如公式（3）

對于輸出層節點，處理方式與隱含層相同，ωij的權重調整公式如下：

其中ωij為更新后的權值，為學習率，0＜η＜1，對于δj的處理，要從輸出節點和非輸出節點考慮。

對于輸出節點δj表示為：

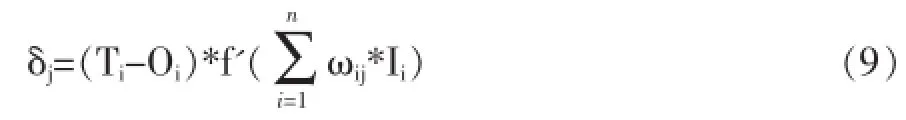
對于非輸出型節點δj表示為：

其中Ti和Oi分別表示網絡期望輸出和實際輸出。對于輸出節點。迭代到什么時候為止，僅僅當公式（7）達到要求的精度則結束。

4 基于粗集神經網絡的信用評價模型構建

在科技金融領域對科技型企業進行信用風險評估過程中，由于每個企業提供的企業信用指標存在多樣性和不確定性，因此造成數據指標在收集時也會出現各種缺陷和錯誤，通過數據整理，其多樣性和不確定性主要表現為以下幾個方面：一、由于每個企業對于財務指標的定義沒有統一，很多企業的財務指標沒有統一；二、是由于財務工作人員的原因財務指標數據記錄錯誤；三、由于企業工作人員工作粗心造成該記錄的地方空白，記錄為空（NULL）；對于上述數據，作者對上述數據作了簡單的處理，有些進行統一，有些進行了刪除，處理之后剩下表1的29個指標，并用｛x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11，x12，x13，x14，x15，x16，x17，x18，x19，x20，x21，x22，x23，x24，x25，x26，x27，x28，x29｝表示條件屬性，具體表示意義如表1。

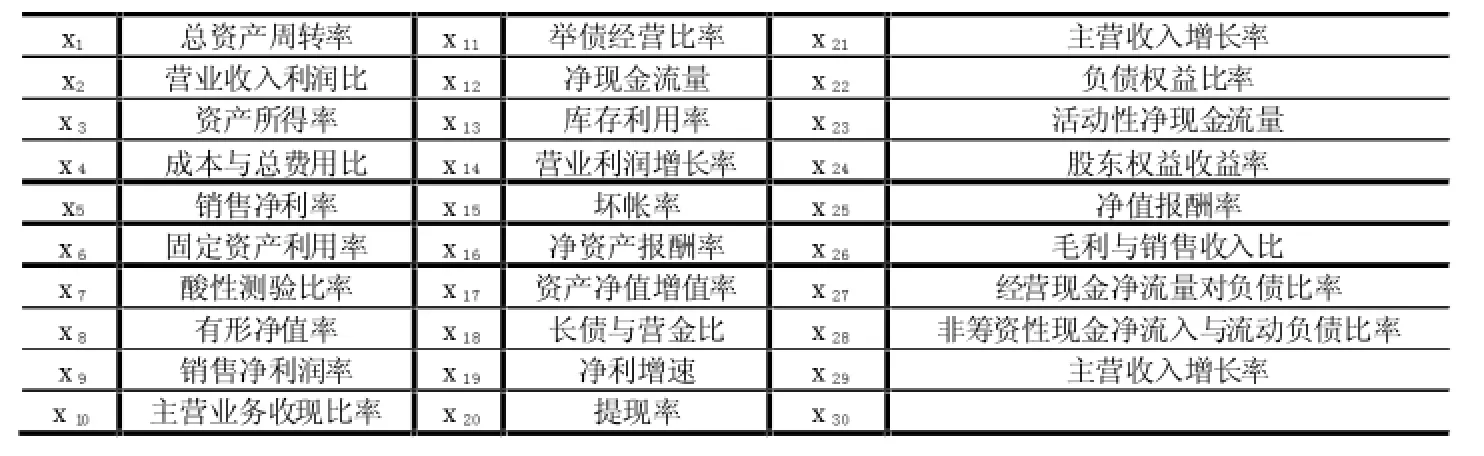
表1 深圳某科技金融機構收集的企業指標

由于上述提供的數據是連續數據，因此必須對上述數據進行離散化處理［9］。將上述指標數據分為5檔，為了避免因為有些數據過大或者過小從而導致離散數據失真，本文暫不考慮偏離數據，先將大部分數據離散后再對偏離數據進行處理，因此每個指標有5等份；而對于決策屬性D用有信用和無信用來處理，分別用1 和0表示，對文中用到的等區間法可以借鑒王妍提出的處理方法［10］。

（1）條件屬性約簡

對于知識系統R，令R=｛x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11，x12，x13，x14，x15，x16，x17，x18，x19，x20，x21，x22，x23，x24，x25，x26，x27，x28，x29，D｝，因此在知識系統R中，條件屬性為C=｛x1，…x29｝，值屬性為D，條件屬性C對論域U的劃分 為 C/D=｛｛x1｝，｛x2｝，｛x3｝，｛x4｝，｛x5｝，｛x6｝，｛x7｝，｛x8｝，｛x9｝，｛x10｝，｛x11｝，｛x12｝，｛x13｝，｛x14｝，｛x15｝，｛x16｝，｛x17｝，｛x18｝，｛x19｝，｛x20｝，｛x21｝，｛x22｝，｛x23｝，｛x24｝，｛x25｝，｛x26｝，｛x27｝，｛x28｝，｛x29｝｝，對于信用風險評價模型中對于指標的約簡，其思想來源于Pawlak關于重要度的理論，其具體的實現如下：

（1）計算C對D的核CORED（C）；

（2）令B=CORED（C），posB（D）=posc（D），接著轉（5）；

（3）如果?ci∈C/B.，計算重要度sig（ci，B）=|posB∪｛ci｝|-|posB（D），同時計算，令B=B∪（Cm）；

（4）若posB∪｛ci｝（D）≠posB（D），轉至（3）；

（5）若輸出B∈REDc（D），則結束。

本文收集了深圳近10年來的40家非上市科技型公司的財務數據，按表1提到的指標整理成知識庫，再應用上述約簡算法，得到知識庫的核為REDc（D）=｛x1，x9，x13，x15，x18，x20，x22，x24｝

表1中的所有指標按照上述步驟進行處理，得到REDc（D=｛x1，x9，x13，x15，x18，x20，x22，x24｝。根據粗糙集的約簡理論，要使知識系統保持分類不變情況下，可以認為知識系統依賴于 x1，x9，x13，x15，x18，x20，x22，x246等 8個指標。

（2）應用BP分類

完成上述約簡之后，接著應用BP神經網絡對知識庫進行分類，首先將上述40家公司的8個指標數據進行預處理，將所有的數據映射到［0，1］區間。

本文采用十折交叉驗證的方法進行訓練，輸入神經元為8條，由于是一個二分類問題，因此輸出神經元只要1條就可以，本文設置學習率為，η=0.8，學習總誤差E（K）≤0.001。具體的訓練如下：

（1）初始化神經網絡，設置BP中各個節點及各個權值的初始值，文中采用均勻分布隨機數，但是要保證BP網絡的加權值達到飽和。

（3）將數據集中的數據在網絡中訓練時，利用公式（2）（3）逐步條件各個權值和節點值。

（4）然后利用公式（5）（6）計算輸出節點和非輸出節點的誤差。

（5）當總誤差當總誤差E（W）≤0.001則迭代結束，否則進入（3）進行下一迭代。

5 實證分析

為了對本文模型進行有效地驗證，本文選取了深圳證券交易所的100個科技型公司的數據作為測試數據集進行驗證，其中有20家ST科技型公司和80個非ST科技型公司。為了驗證本文模型的有效性，現分別將傳統的BP神經網絡與基于粗集神經網絡應用于同一測試數據集，實驗平臺采用 Intel Pentium CPU3.2GHz，內存為2GB，OS為Windows XP，以MATLAB 7為仿真軟件。實驗結果如圖3和表2所示，從圖3中可以看出，基于粗糙集的BP神經網絡在識別率上都優于傳統的BP神經網絡，且隨著測試數據的增加，其識別率也不斷提高。

測試時間如下表2所示，從表2可以看出，基于粗糙集的BP神經網絡測試所用的時間明顯比傳統的BP神經網絡的測試時間要少，主要原因是因為應用粗糙集約簡了知識庫的指標，簡化了網絡，從而減少了訓練時間和測試時間。

圖3 風險控制子系統檢測結果圖

6 結語

（1）將粗糙集理論與BP神經網絡有機結合，構建了基于粗糙集與BP的信用風險評價模型，其中利用粗糙集約簡可以在不減少分類能力情況下有效地簡化了BP神經網絡的復雜度，從而有效地減少了數據采集成本和信用審批成本，有利于科技金融服務工作的迅速開展，更有利于生存創造一定的條件。

（2）實例表明，將本文模型與傳統的BP神經網絡信用評價模型進行比較，無論在評價的識別率還是評價時間上，本文模型在科學性、合理性及可操作性上都具有一定的優勢。

（3）本文在科技金融服務機構如何對企業信用風險進行評價方面做了一次有益的探索，對日后相關課題具有一定的參考價值。

表2 粗集神經網絡模型與傳統BP神經網絡測試時間比較（單位：s）

［1］盧超，鐘望舒.提出的商業銀行對中小企業信用風險評價的方法探索［J］.金融論壇，2009，（9）：13-20.

［2］樓際通，樓高文，余銹榮.商業銀行個人信用風險評價的投影尋蹤建模及其實證研究［J］.經濟數學，2013，30（4）：26-32.

［3］曾詩鴻，王芳.基于KMV模型的制造業上市公司信用風險評價研究［J］.預測，2013，32（2）：61-64.

［4］朱天星，于立新，田慧勇.商業銀行個人信用風險評價模型研究［J］.問題探討，

［5］郭志軍，何昕，魏仲慧.一種基于粗糙集神經網絡的分類算法［J］.計算機應用研究，2011，28（3）：838-850.

［6］王國胤，姚一豫，于洪.粗糙集理論與應用研究綜述［J］.計算機學報，2009，32（7）：1229-1246.

［7］張建華.知識管理中的知識進化績效評價機制研究［J］.科學學與科學技術管理2013，34（7）：28-36.

［8］張卉.基于粒子群優化BP神經網絡的房價預測［J］.價值工程，2012（5）：207～208.

［9］于錕，劉知貴，黃正良.粗糙集理論應用中的離散化方法綜述［J］，2005，20（4）：32-36.

［10］王妍，潘瑜春，王惠.基于Voronoi和信息滴的空間群樣點檢測［J］.計算機工程與設計，2010，31（18）.：45-49.

WANG Jie1，CHEN Gang2
（1.Dongguan Electronic Computing Center，Dongguan 523123；2.Department of Computer Technology，Guangdong Polytechnic Institute，Zhongsan 528458）

Now the current credit approval has low efficiency and cost too much，the reasons for that is bad enterprise credit evaluation model，too much evaluation index and too long evaluation time；To solve this problem，proposes a new credit evaluation model based on rough sets and BP，the model effectively reduces financial indicators of enterprises without affecting the classification attributes，at the same time，uses BP neural network fault tolerant ability，well classified the credit businesses.At last，puts this model to application，the results show that the model is effective.

Technology Finance；Risk Evaluation；Rough Set；Neural Network

國家創新基金（No.13C26214404497）、國家自然科學基金項目（No.61175027）

1007-1423（2016）21-0003-06

10.3969/j.issn.1007-1423.2016.21.001

王潔（1962-），女，廣東增城人，副研究員，博士研究生，研究方向為科技管理與服務

陳剛（1977-），男，江西高安人，博士研究生，副教授，研究方向為人工智能、數據挖掘

2016-05-16

2016-07-11Research on Credit Risk Evaluation System Based on Rough Set and BP