相對論重離子碰撞夸克膠子等離子體對磁場分布的影響

陳　勛，馮笙琴

(三峽大學 理學院，湖北 宜昌 443002)

?

相對論重離子碰撞夸克膠子等離子體對磁場分布的影響

陳勛，馮笙琴

(三峽大學 理學院，湖北 宜昌 443002)

首先利用Woods-Saxon分布，計算相對論重離子碰撞磁場空間分布；并在此基礎上考慮夸克膠子等離子體(QGP)的響應，假定QGP為理想導體情況下，研究磁場在QGP環境下的分布特征。

Woods-Saxon分布；QGP響應； 磁場分布

當兩個重離子以非零的碰撞參量且以接近光速碰撞時， 沿著角動量方向會產生巨大的電磁場[1-3]。如果在這個情況下，出現了不為零的手征性，沿著磁場方向將會產生電磁流，這種現象稱為手征磁效應[4-6]。

一些文獻[7-12]認為出現退禁閉相變和手征磁相變的重要信號是手征磁效應，此時會出現沿著角動量方向的帶電粒子有傾向性的發射，導致產生局域的非零的手征性。所以文獻[7-12]認為手征磁效應是出現退禁閉相變和手征磁相變的必要條件。

在一些計算中，往往忽略了電磁場對產生物質的相應，即認為所產生的物質是不導電的絕緣體。實際情況往往不是這樣的，如果產生的物質是夸克膠子等離子體(QGP)，對應的電導率是不能忽略的。很多情況下，我們應該考慮產生的QGP物質對磁場的響應。

本文采用文獻[8]中修正的手征磁場計算方法，計算了非中心相對論重離子碰撞的磁場，并考慮一種特殊情況下σ→∞的QGP對磁場的響應，并計算了此種情況下的磁場分布特征。

1　手征磁場計算

當兩個原子核以接近光速進行對撞時，對應的洛侖茲收縮因子γ很大，我們可以把原子核看成是兩個薄餅，對應核分布取Woods-Saxon分布[13]：

(1)

這里d=0.54fm，n0=0.17fm-3，半徑R=1.12A1/3fm。考慮洛倫茲收縮，二維平面由圖1給出，對應的二維電荷密度分布為：

(2)

N為歸一化常數。相對論核-核碰撞產生的總磁場為：

(3)

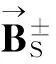
(4)

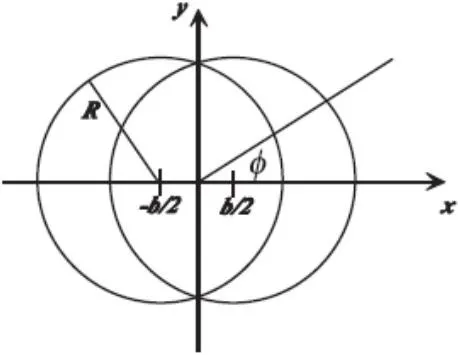
圖1非對心相對論重離子碰撞的沿著z方向橫截面視圖

注：兩核有相同半徑R朝著相反方向移動。碰撞參數為b，角φ是關于反應截面的方位角兩個核重疊區域為包含參與者，沒重疊區域為旁觀者。

參加反應核子對磁場的 y 方向分量的貢獻為：

(5)

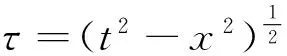
(6)

為一個階躍函數，和

(7)

為參加反應的核子沿著碰撞軸方向的快度分布。

2　QGP中磁場的響應

討論QGP對重離子碰撞產生磁場的響應，對應的麥克斯韋方程為：

(8)

(9)

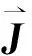
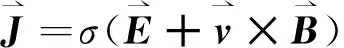
(10)

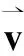
(11)

(12)

(13)

其中，L是QGP的時間標度或者稱為特征長度，u是流體特征速度。在高溫微擾QCD計算[14]中，給出σ≈6T/e2，這表明溫度越高，對應的電導率越大。文獻[15]中，DengWeiTian和HuangXuGuang等人給出了在Rm?1情況下，也即是忽略掉方程(11)和(12)中擴散項，取QGP為理想導體，即在σ→∞情況下的方程為：

(14)

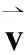
(15)

(16)

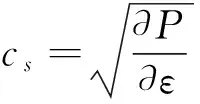
(17)

這里ax,y是橫向分布的均方根寬度。

通過聯立方程(16)和(17)得到：

(18)

(19)

(20)

(21)

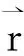
(22)

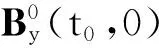
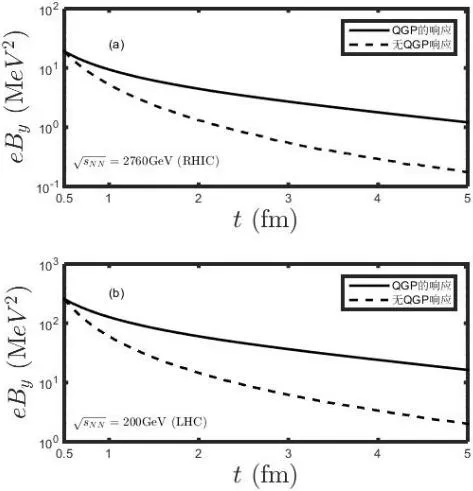
圖=2760 GeV(a)和的中心點磁場隨時間變化關系曲線

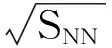
圖3　Au-Au碰撞在t=5fm磁場的空間分布(考慮QGP響應后，

3　結論和分析

本文首先討論了QGP對磁場響應，給出了QGP為理想導體情況下的磁場時空分布關系公式。然后以中心點磁場隨時間變化特征為例，比較了考慮QGP響應后與不考慮磁場響應的磁場變化特征，可以清晰看到，QGP響應使磁場隨時間改變的減弱效應降低。還討論了磁場空間分布特征，與以前不考慮QGP響應的磁場空間分布相比，考慮QGP響應的磁場空間分布具有明顯不同的分布特征。中心點為分布峰，隨著x和y的增大，磁場逐漸減小。

[1]KharzeevDE,MclerranLD,WarringaHJ.Theeffectsoftopologicalchargechangeinheavyioncollisions:EventbyeventPandCPviolation[J].NuclearPhysicsA, 2008, 803(3-4):227-253.

[2]SkokovVV,IllarionovAYU,ToneevVD.Estimateofthemagneticfieldstrenthinheavy-ioncoliision[J].InternationalJournalofModernPhysicsA, 2009, 24(31):5925-5932.

[3]MinakataH,MullerB.Disorientedchiralcondensateandstrongelectromagneticfields[J].PhysicsLettersB, 1995, 377(1-3):135-139.

[4]KharzeevD.ParityviolationinhotQCD:Whyitcanhappen,andhowtolookforit[J].PhysicsLettersB, 2006, 633(2-3):260-264.

[5]KharzeevD,ZhitnitskyA.ChargeseparationinducedbyP-oddbubblesinQCDmatter[J].NuclearPhysicsA, 2007, 797(1-2):67-79.

[6]KenjiKharzeev,DmitriEWarringa,HarmenJ.TheChiralMagneticEffect[J].PhysicsofAtomicNuclei, 2008, 75(5):607-612.

[7]BurnierY,KharzeevDE,LiaoJ, et al.Chiralmagneticwaveatfinitebaryondensityandtheelectricquadrupolemomentofthequark-gluonplasma[J].PhysicalReviewLetters, 2011, 107(5):2311-2314.

[8]KharzeevDE,SonDT.Testingthechiralmagneticandchiralvorticaleffectsinheavyioncollisions[J].PhysicalReviewLetters, 2011, 106(6):426-431.

[9]BasarG,DunneGV,KharzeevDE.ChiralMagneticSpiral[J].PhysicalReviewLetters, 2010, 104.

[10]FukushimaK,KharzeevDE,WarringaHJ.Real-timedynamicsofthechiralmagneticeffect[J].PhysicalReviewLetters, 2010, 104(21):4482-4482.

[11]FukushimaK,KharzeevDE,WarringaHJ.Electric-currentsusceptibilityandtheChiralMagneticEffect[J].NuclearPhysicsA, 2009, 836(s3-4):311-336.

[12]WarringaHJ.DynamicsoftheChiralMagneticEffectinaweakmagneticfield[J].PhysicalReviewDParticles&Fields, 2012, 86(86):525-541.

[13]MoYJ,FengSQ,ShiYF.EffectoftheWoods-SaxonnucleardistributiononthechiralmagneticfieldinRelativisticHeavy-ionCollisions[J].PhysicalReviewC, 2013, 88(88):101-108.

[14]ArnoldPB,MooreGD,YaffeLG.Effectivekinetictheoryforhightemperaturegaugetheories[J].JournalofHighEnergyPhysics, 2003, 1(01):816-825.

[15]DengWT,HuangXG.Event-by-eventgenerationofelectromagneticfieldsinheavy-ioncollisions[J].PhysicalReviewC, 2012, 85(85):144-149.

[16]OllitraultJY.Relativistichydrodynamicsforheavy-ioncollisions[J].EuropeanJournalofPhysics, 2007, 29(2):275-302(28).

[17]ZhongY,YangCB,CaiX, et al.SpatialdistributionsofmagneticfieldintheRHICandLHCenergyregions[J].ChinesePhysicsC, 2014, 39(10):61-67.

責任編輯王菊平

Effect of quark gluon plasma on the magnetic field distributionin relativistic heavy ion collisions

CHEN Xun， FENG Sheng-qin

(College of Science, China Three Gorges University, Yichang 443002, Hubei, China)

Spatial distributions of magnetic field are calculated in relativistic heavy ion collision based on Woods-Saxon distribution. We further study the characteristics of magnetic field distribution while considering Quark gluon plasma (QGP) as an ideal conductor response in a QGP environment.

Woods-Saxon distribution; QGP response; magnetic field distribution

O571.6

A

1003-8078(2016)03-0061-05

2016-04-27

10.3969/j.issn.1003-8078.2016.03.16

陳勛，男，湖北黃石人，碩士研究生，主要研究方向為高能核物理。

馮笙琴，男，湖北黃梅人，教授，主要研究方向為高能核物理。

國家自然科學基金項目 (11475068, 11247021)；教育部夸克-輕子重點實驗室項目(華中師范大學 QLPL2014P01)。