一類具有間斷系數的周期Hilbert邊值逆問題的研究

趙　爽

(綏化學院 農業(yè)與水利工程學院，黑龍江 綏化 152061)

?

一類具有間斷系數的周期Hilbert邊值逆問題的研究

趙爽

(綏化學院 農業(yè)與水利工程學院，黑龍江 綏化 152061)

文章給出了具有間斷系數的周期Hilbert邊值逆問題在單位圓周上的數學提法，應用周期延拓、保形變換等方法將問題轉化為經典的Riemann邊值問題，并據其理論，討論了具有間斷系數的周期Hilbert邊值逆問題的可解性，給出了該類邊值問題的可解條件及其在正則情況下的一般解。

Hilbert邊值逆問題；周期；間斷系數

解析函數邊值問題在研究平面彈性和斷裂力學等實際問題中發(fā)揮著重要的作用[1]。近年來，有關解析函數的各類邊值問題得到了長期深入的研究及廣泛的推廣。翟小云等[2]研究了解析函數的周期復合邊值問題的求解問題。筆者[3]研究了具有間斷系數的周期復合邊值問題的求解問題。王明華[4-5]教授對邊值逆問題做了更深入的研究，給出了解析函數的一類Riemann-Hilbert邊值逆問題的數學提法及其解法。本文在上述工作的基礎上，結合筆者研究的單位圓周上周期Hilbert邊值逆問題的方法[6]，把具有間斷系數的周期問題與Hilbert邊值逆問題結合在一起研究，并且得到這類問題在正則情況下的一般解。

1　提出問題

所求問題為：求函數對(Φ(z),Ψ(t))，這里Φ(z)是在D+內以απ為周期的分區(qū)全純函數，Ψ(t)為Γk上H類實函數，也以απ為周期，滿足下列條件:

(1)

其中已知函數λj(t)=aj(t)+ibj(t),aj(t),bj(t),sj(t),rj(t)(j=1,2)∈H(Γk)，均以απ為周期，且在Γk上存在有限個第一類間斷點。

為方便，記

(2)

這里本文只討論正則型問題的解，即λ(t)≠0,r(t)≠0時問題的解。

2　分析轉化問題

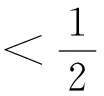
此時已知實函數aj(t),bj(t),sj(t),rj(t)(j=1,2)在Γ0上仍存在著有限個第一類間斷點，將這些間斷點記為c1,c2,…,cn，于是所求問題轉化為在h(c1,c2,…,cq)類中求解(Φ0(z),Ψ0(t))。

其次用變換

(3)

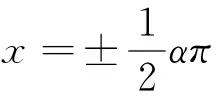
(4)

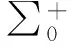
3　求解問題

設問題(4)的指標為κ，則它也為原問題(1)的指標。

將式(4)中的第一式兩端乘以r2(τ)與第二式兩端乘以r1(τ)后相減，則式(4)化為帶間斷系數的Hilbert邊值問題：

(5)

其中

(6)

3.1齊次問題的解，即s1(t)=s2(t)=0時的解

由文獻[6]知，當κ≥0時，齊次問題(5)的一般解

(7)

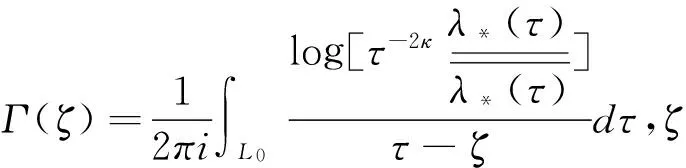
將其帶回式(4)得

(8)

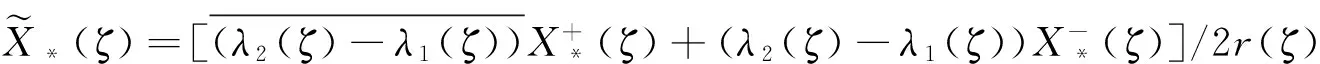
當κ<0時，齊次問題(5)只有零解，從而所求問題(1)只有零解。

3.2非齊次問題的解

根據非齊次方程通解的結構，這里只須求出問題(5)的一個特解即可。由文獻[6]知，當κ≥0時，問題(5)有滿足條件的特解

(9)

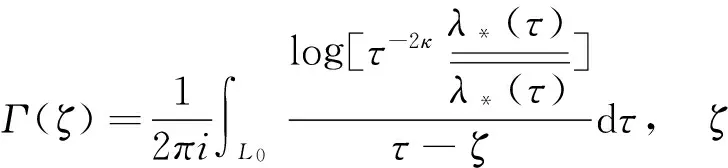
將其帶回式(4)得

(10)

其中

(11)

當κ<0時，問題(5)可解的條件為

(12)

(13)

其中k=-κ-1時為實方程，即式(13)為-2κ-1個條件，在此條件下，問題(4)有唯一解。

4　結論

根據以上分析，可得下述定理。

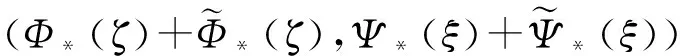
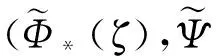
最后用變換(3)的逆變換將等價問題(4)的一般解代回原問題(1)中，即可得到原問題(1)在正則性問題的一般解。

本文首先給出了帶間斷系數的的周期Hilbert邊值逆問題在的數學提法，然后利用周期延拓和保形變換等方法把所求問題轉化為求解一般的Hilbert邊值逆問題，從而給出了一般解的表達方式及可解條件，最后得到了此類問題的一般解。

[1]路見可.解析函數邊值問題(第二版)[M].武漢：武漢大學出版社，2004.

[2]翟小云，鄭神州.解析函數的周期復合邊值問題[J].北京交通大學學報，2005，29(3)：54-58.

[3]趙爽.具有間斷系數的周期復合邊值問題[J].高師理科學刊，2009，29(6)：28-31.

[4]Wang minghua. The inverse riemann boundary value problem for bianalytic functions[J]. 四川師范大學學報(自然科學版)，2003，26(2)：132-134.

[5]王明華.一類Riemann-Hilbert邊值逆問題[J].純粹數學與應用數學，2006，22(4)： 532-535.

[6]趙爽，張姮妤，丁慧，等. 單位圓周上的周期Hilbert邊值逆問題的研究[J].綏化學院學報，2013，33(11)：156-160.

責任編輯王菊平

Research of a cycle Hilbert boundary value problem on the discontinuous coefficient inverse

ZHAO Shuang

(College of Agricultural and Hydraulic Engineering, Suihua University, Suihua 152061，Heilongjiang, China)

The mathematical definition of Hilbert boundary value inverse problem for the upper half plane with discontinuous coefficient was discussed in this paper. Methods of period and conformal transformation were applied to convert the problem into Riemann boundary value problem. Based on the theory, the solvability of the inverse Hilbert boundary value problem with discontinuous coefficients was discussed. The solvability conditions of the problem and its general solution in the case of regular were obtained.

Hilbert boundary value inverse problem；cycle；discontinuous coefficient

O174.5

A

1003-8078(2016)03-0001-03

2015-11-24

10.3969/j.issn.1003-8078.2016.03.01

趙爽，女，黑龍江蘭西人，講師，碩士，主要研究方向為函數論。

綏化學院杰出青年基金項目(SJ11005)。