AxMn1-xFe2O4鐵氧體(A=Zn，Ni)中陽離子的占位有序化行為研究

陳祖華　方　圓　吳　波＊,　吳育鋒　范志宇　薩百晟　鄭福南　黃錦濤

(1福州大學材料科學與工程學院，福州　350100)(2廈門TDK有限公司，廈門　361021)

AxMn1-xFe2O4鐵氧體(A=Zn，Ni)中陽離子的占位有序化行為研究

陳祖華1方圓1吳波＊,1吳育鋒1范志宇1薩百晟1鄭福南2黃錦濤2

(1福州大學材料科學與工程學院，福州350100)
(2廈門TDK有限公司，廈門361021)

基于尖晶石晶體結構信息，本文采用熱力學三亞晶格模型，將材料熱力學計算和第一性原理計算相結合，研究了ZnxMn1-xFe2O4和NixMn1-xFe2O4立方相中的Zn2+、Ni2+、Mn2+以及Fe3+在8a和16d亞晶格上的占位有序化行為。結果表明：在錳鐵氧體中，室溫下Mn2+完全占據在8a亞晶格上，Fe3+完全占據在16d亞晶格上，屬于正尖晶石結構；隨著熱處理溫度升高，在1 273 K達到熱處理平衡時的占位構型為(Fe3+0.09Mn2+0.91)[Fe3+1.91Mn2+0.09]O4，在熱處理溫度升至1 473 K時，達到熱處理平衡時的占位構型為(Fe3+0.11Mn2+0.89)[Fe3+1.89Mn2+0.11]O4，均與實驗結果符合較好。在鋅鐵氧體中，室溫下Zn2+完全占據在8a亞晶格上，Fe3+完全占據在16d亞晶格上，屬于正尖晶石結構；在熱處理溫度較高時，Zn2+和Fe3+發生部分置換，符合實驗結果。在鎳鐵氧體中，半數的Fe3+在室溫下占據在8a亞晶格上，Ni2+與剩下另一半的Fe3+共同占據在16d亞晶格上，僅在熱處理溫度較高的時候發生微弱變化，亦與已有的實驗結果吻合。在此基礎上，本文進一步通過熱力學模型研究了立方相尖晶石結構的ZnxMn1-xFe2O4、NixMn1-xFe2O4復合體系中陽離子占位行為與熱處理溫度對占位的影響規律。

尖晶石；錳鋅鐵氧體；占位有序化行為；熱力學模型；第一性原理計算

0　引　言

軟磁鐵氧體是軟磁材料的典型代表[1]，由于其具有高磁導率、高飽和磁感強度、低矯頑力和低損耗等優點，因此，被廣泛用于各種電感元件如濾波器磁芯、變壓器磁芯、天線磁芯、磁帶錄音和錄像磁頭以及多路通訊等的記憶磁頭磁芯等，在電子工業中的應用具有悠久歷史，并且日益廣泛[2-3]。隨著電子信息技術的飛速發展，電子設備趨向集成智能化、小型輕量化發展，對高性能軟磁鐵氧體材料的要求也越來越高。因此，從理論上弄清軟磁鐵氧體的微結構和性能[4-6]，有助于加速高性能低成本軟磁鐵氧體的研究開發。

眾所周知，離子或原子在亞晶格上的占位行為對材料的性能具有重要的影響。由于制備樣品的粒徑尺寸效應和熱處理工藝的影響[7]，尖晶石結構的鐵氧體化合物中陽離子的分布具有多樣性。因此，對尖晶石結構的鐵氧體化合物中陽離子在亞晶格上的占位有序化行為的研究結果也具有一定的差異性[8-9]。在理論研究方面，Seko等采用團簇擴張法結合第一性原理計算的方法，研究了六種不同成分的尖晶石氧化物[10]，其研究結果表明MgGa2O4和MgIn2O4是四方相的反式尖晶石結構，而MgAl2O4，ZnAl2O4，ZnGa2O4和ZnIn2O4是立方相的正尖晶石結構。Wei等用反置能量(Inversion Energy)來判斷某一體系的尖晶石結構化合物是屬于正尖晶石結構還是反尖晶石結構[11]，并且基于SQS(Special Quasirandom Structure)近似方法，具體研究了AⅡBⅢ2O4和AⅣBⅡ2O4系列尖晶石結構中的陽離子分布，其中研究的元素包括第Ⅱ主族中的Mg、Zn和Cd元素，第Ⅲ主族中的Al、Ga、和In元素,以及第Ⅳ主族中的Si、Ge和Sn元素。Wei等采用XRD分析方法研究了在1 523 K下制備的NixMn1-xFe2O4鐵氧體中陽離子的占位分布情況，并采用熱力學計算的方法，分析了1 523 K下該體系鐵氧體中陽離子的占位有序化行為，其與實驗結果吻合得較好[12]。但是，其熱力學推導過程在建模時需要基于反應平衡常數等一些實驗參數，并且，它假設Ni在8a亞晶格上的占位分數為0，這些都是依賴于實驗與經驗。

本文基于立方相尖晶石的晶體結構信息，通過建立熱力學亞晶格模型，輔助以第一性原理計算，來定量化研究AxMn1-xFe2O4鐵氧體A=Zn，Ni)中陽離子在亞晶格上的占位有序化行為隨成分和溫度的變化規律，以期為AxMn1-xFe2O4鐵氧體(A=Zn，Ni)軟磁材料的配方設計和性能調控提供理論指導。

表1　立方相尖晶石結構鐵氧體的晶體學結構信息Table 1 Spinel(MgAl2O4-H11)Structure

1　計算模型和計算方法

1.1計算模型

本文研究立方相尖晶石結構的鐵氧體中陽離子在亞晶格上的占位有序化行為，其晶體結構信息如表1所示，其單胞結構如圖1所示。該結構為立方結構，其中氧離子構成面心立方密堆垛結構，共有64個四面體間隙和32個八面體間隙。關于尖晶石結構中，離子的等效Wyckoff位置和內坐標參數的選取和轉換方法，Sickafus等進行了詳細的介紹[13]，根據陰離子坐標u的對稱性，當u的對稱性分別為-43m和-3m時，分別對應于兩種亞晶格模型，即8a、16d、32e和8b、16c、32e。在完全有序的錳鐵氧體尖晶石結構中，本研究將Mn2+填充在其1/8的四面體間隙中，用Wyckoff晶位8a表示；Fe3+填充在1/2的八面體間隙中，用Wyckoff晶位16d表示；而氧離子Wyckoff晶位用32e表示。基于上述3套Wyckoff亞晶格位置，即8a、16d、32e，本文建立出立方相尖晶石結構鐵氧體的亞晶格模型。

圖1　MnFe2O4的晶體結構Fig.1 Crystal structure of MnFe2O4

本文基于晶體學結構信息，采用亞晶格模型研究鐵氧體中陽離子在亞晶格上的占位有序化行為。亞晶格模型，也稱為化合物能量模型(Compound Energy Formalism)[14]，可以用于預測化合物中各組元在各個亞晶格中的占位分數，進而研究元素的占位有序化行為。亞晶格模型可以用表達式(1)表示：

對于立方相尖晶石結構鐵氧體，W1=8a、W2=16d 和W3=32e。根據文獻報道，氧元素完全占據在32e亞晶格上，因此本文將氧離子固定在32e亞晶格上，以錳鋅鐵氧體為例，金屬陽離子的占位模型如表達式(2)所示：

根據熱力學條件，由室溫下穩定結構的純組元形成化合物的Gibbs自由能如公式(3)所示：

其中，ΔH為生成焓，ΔS為形成熵，T為溫度。由于直接求解ΔG是困難的，本文根據熱力學狀態函數的固有性質，即熱力學量的大小只與始末態有關，而與中間過程無關的這一特性，設計一條等效路徑來間接計算出化合物的Gibbs自由能。根據熱力學亞晶格模型，定義一系列端基化合物[14]，即某一種點陣上只被一種元素占據，根據排列，m種陽離子在n種亞晶格上的占據，其排列端基數為mn。由于氧離子的占位是確定的，僅需考慮體系中陽離子在8a和16d兩種亞晶格上的占位行為。因此，對于錳鋅鐵氧體，m=3，n=2。借助于端基化合物這一中間過程，將元素形成化合物的過程，分解為由元素先形成端基化合物，然后再由端基化合物組裝形成復雜化合物這樣一個等效的替換途徑來間接計算出化合物的Gibbs生成自由能，計算轉換途徑如圖2所示。

圖2　熱力學函數計算路徑轉換示意圖(其中反應路徑③可以轉換為由路徑①和路徑②聯合來實現，即③=①+②)Fig.2 Alternative computing path of thermodynamic function denoting③=①+②

因此，ΔH的表達如公式(4)所示：

其中，ΔH(k∶l∶m)為室溫穩定結構的純組元生成端基化合物的生成焓，ΔEH為由室溫穩定結構的純組元生成錳鋅鐵氧體的過剩焓，由于過剩焓的值很小，因此本文不予考慮[15]。

Jain等指出，溫度和壓力對固相材料的熱容影響非常微弱[16]，而且Lany等計算出來的ΔH298 K和ΔH0 K差值一般小于0.03 eV·atom-1[17],因此本文只考慮0 K下的生成焓，并由公式(5)計算得到，公式(5)為：

其中，ΔH(k∶l∶m)，Etot(k)，Etot(l)和Etot(m)分別為端基化合物和相應純組元的總能，其單位為eV·atom-1。

同理，忽略由室溫穩定結構的純組元生成錳鋅鐵氧體的過剩熵，將化合物的生成熵近似簡化為體系的混合熵[18-19]，即如公式(6)所示:

體系的混合熵如公式(7)所示:

其中，R為波爾茲曼常數，R=8.6194×10-5eV·K-1· atom-1。將公式(4)和(7)代入公式(3)，求得體系的Gibbs自由能，其中包含了占位分數與溫度兩種變量，如公式(8)所示：

另一方面，根據質量守恒定律和歸一化約束條件，可以得到公式(9)～(16)：

有序-無序轉變達到熱力學平衡時，Gibbs自由能最小化，因此根據極值條件獲得偏微分方程組，如公式(17)所示：

通過第一性原理總能計算(詳見1.2)，建立出端基化合物的生成焓熱力學數據庫后，對于任一給定成分和相平衡溫度條件的鐵氧體化合物，求解由公式(9)～(17)所組成的方程組，即可得到陽離子在各個亞晶格上的占位分數，如公式(18)所示：

1.2計算方法

本文采用基于密度泛函理論的第一性原理計算方法，選用VASP (Vienna Ab-initio Simulation Package)[20]來計算5個純組元(Mn、Fe、Ni、Zn、O)和相應的16個端基化合物的總能，進而獲得由純組元形成各個端基化合物的生成焓。對于每一種端基化合物，均考慮鐵磁態，亞鐵磁以及反鐵磁態這3種狀態，并選取總能最低時的狀態作為端基化合物的穩定態。交換關聯勢采用廣義梯度近似(Generalized Gradient Approximation，GGA)[21]的Perdew-Burke-Ernzerh(PBE)形式來描述，即贗勢庫文件取PAW-PBE模式。進行總能計算時，對端基化合物，K空間的撒點采用6×6×6 Monkhorst-Pack模式，對室溫穩定態的純組元Mn_BCC的K空間的撒點采用5×5×5 Monkhorst-Pack模式，Fe_BCC、Ni_FCC 和Zn_HCP的K空間的撒點均采用12×12×12 Monkhorst-Pack模式，而O2采用4×4×4的Gamma模式，截斷能均設置為520 eV。對原子位置、晶胞體積進行弛豫，保持形狀仍為立方尖晶石結構。同時，開啟自旋極化，初始磁矩依據陽離子的孤對電子數進行設定。計算結果保證總能關于截斷動能和K點產生模式的收斂精度達到1 meV·atom-1。

事實上，建立出端基化合物的生成焓熱力學數據庫后，直接對由公式(9)～(17)構成的偏微分方程組進行手工求解難度較大。但是，隨著計算材料學的快速發展,已有專業的熱力學計算軟件[22],如Thermo-Calc和Pandat，能夠較為方便地求解這類熱力學偏微分方程組，并直接給出本文所關注的占位分數。因此，本文在建立好格式化的端基化合物生成焓熱力學數據庫后，使用Thermo-Calc軟件包來計算求解占位分數。

2　結果與討論

2.1ZnxMn1-xFe2O4系中的陽離子分布隨溫度變化的規律

ZnxMn1-xFe2O4體系中陽離子在8a和16d亞晶格上的占位分數隨溫度的變化如圖3所示，表格2為本文計算值與現有文獻值的對照表。

圖3　ZnxMn1-xFe2O4體系立方尖晶石中陽離子的占位分數隨熱處理溫度和成分的變化趨勢圖Fig.3 Cation occupying fraction dependence on heat treatment temperature and composition in cubic spinel ZnxMn1-xFe2O4

從圖3可知，當x=0.00時，在室溫下Mn2+完全占據在8a亞晶格上，Fe3+完全占據在16d亞晶格上，錳鐵氧體的陽離子分布表達式為(Mn2+)[Fe3+2]O4，屬于正尖晶石結構，這與Szotek等通過第一性原理的研究，得到錳鐵氧體在正尖晶石結構下能量最低，即8a亞晶格完全被Mn元素占據時最穩定[28]的報道相符。另一方面，高溫下的占位構型如表2所示，亦與已有實驗結果相符合。當x=0.25時，隨著溫度的升高，Mn2+逐漸占據在16d亞晶格上，相應地，Fe3+逐漸占據在8a亞晶格上，而Zn2+表現出強烈地占據在8a亞晶格上，但尚未獲得可靠實驗結果與之對比。本文預測出的Zn2+比Mn2+更加強烈地占據在8a亞晶格上，與Abbas等的研究結果[25]相符合。同時，Henderson等提出，對于大多數的尖晶石結構鐵氧體，陽離子在8a和16d亞晶格上不會表現出完全占據在其中一種亞晶格上,而是表示為(M2+xM3+1-x)[M2+1-xM3+1+x]O4[29]，這與本文對Zn0.25Mn0.75Fe2O4的陽離子占位分布結果相符合。因此，本文預測結果可以為Zn0.25Mn0.75Fe2O4的占位構型提供理論指導。當x=0.5時，室溫下Mn2+與Fe3+即表現了部分反置的占位結果。隨著溫度的升高，占位有序化程度逐漸減弱，而Zn2+的占位傾向對溫度的變化不敏感。當x=0.75時，陽離子的占位分布對溫度并不敏感，絕大多數的Mn2+占據在16d亞晶格上，Fe3+遷移到8a亞晶格上，所有的Zn2+依然保持完全占據在8a亞晶格上。從表2中可以看出，Zn2+和Mn2+與現有文獻值差別較大，而Fatemi等指出，Fe3+與Mn2+的離子分布很容易受到第三組元金屬陽離子濃度的影響[30]，在第三組元金屬陽離子濃度較高時，其會發生反置占據。同時，Lee等指出Mn在低濃度的時候傾向于占據在16d亞晶格上，而在濃度較高時傾向于占據在8a亞晶格上[31]。還有實驗也表明，Mn2+在低濃度的時候傾向于占據在八面體間隙上，而在高濃度的時候傾向于占據在四面體間隙上[32]。上述文獻的占位傾向性研究結果均與本文預測的Mn2+的占位傾向相符合。當x=1時，體系為ZnFe2O4，室溫下Zn2+全部占據在8a亞晶格上，Fe3+元素全部占據在16d亞晶格上，鋅鐵氧體的陽離子分布表達式為(Zn2+)[Fe3+2]O4，與MnFe2O4中陽離子占位分布變化相比，ZnFe2O4中的陽離子占位分布變化受溫度影響較小，與現有文獻中的實驗測試結果和理論計算結果相吻合[33]。

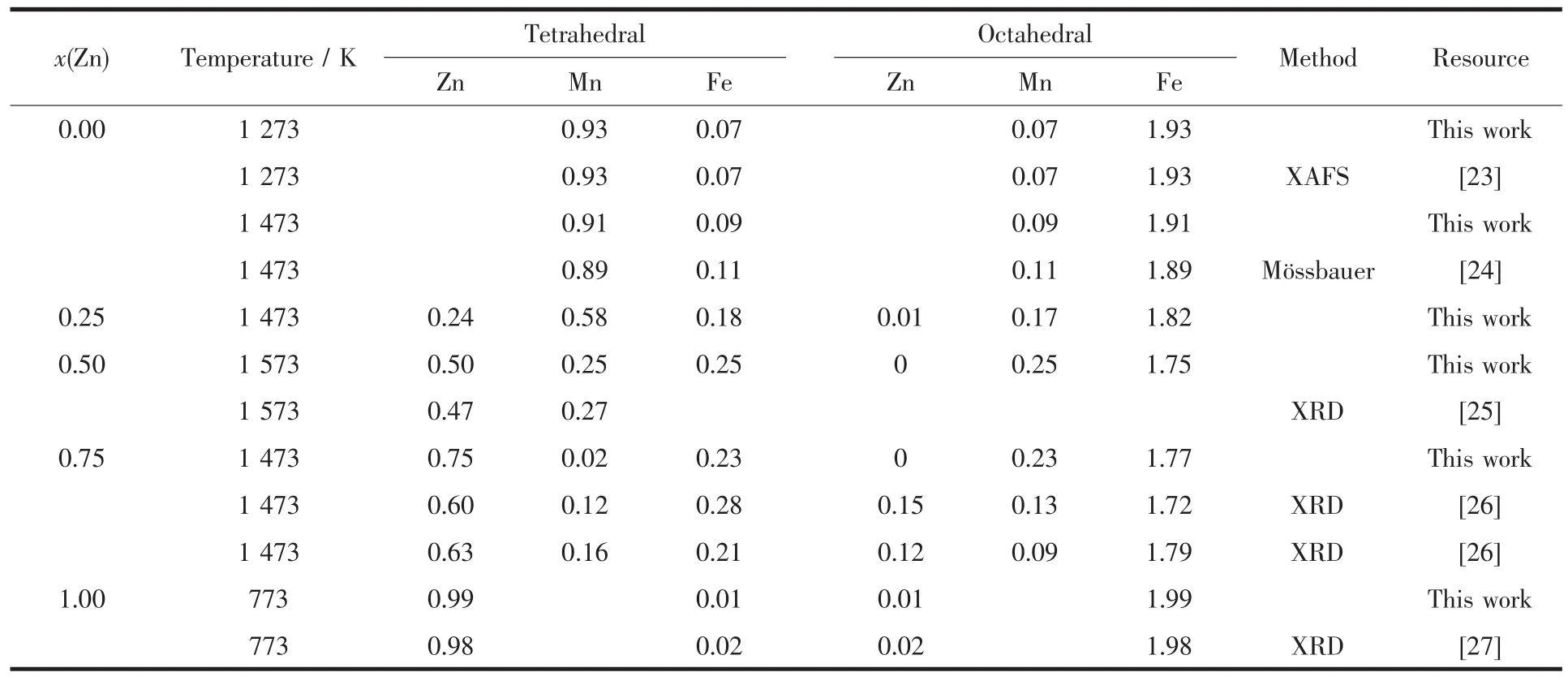
表2　ZnxMn1-xFe2O4體系中的陽離子占位情況Table 2 Site Occupation of ZnxMn1-xFe2O4

2.2NixMn1-xFe2O4系中的陽離子分布隨溫度變化的規律

圖4為不同成分下NixMn1-xFe2O4體系中陽離子在8a和16d亞晶格上的占位分數隨溫度的變化趨勢圖，表3為本文計算值與現有文獻值的對照表。

對比上述計算結果與對應文獻結果發現，各個成分下的NixMn1-xFe2O4(x=0、0.25、0.5、0.75、1)的占位結果均與文獻結果符合得較好。特別對Ni2+的占位傾向預測結果與實驗值相當吻合，證明了NiFe2O4是反式尖晶石結構。對Ni物質的量分數為1時，本文計算結果發現有微量的Ni2+會占據到8a亞晶格，這可能是因為在1 523 K下極少數的Ni2+與Fe3+互相交換位置，占位有序化減弱。但是，隨著溫度下降，由于Ni2+具有強烈占據16d亞晶格的傾向，其可能會隨著溫度降低而重新占據到16d亞晶格上。進一步分析Ni2+、Mn2+和Fe3+的變化規律發現，Ni2+強烈占據在16d亞晶格上，而Mn2+和Fe3+的占位有序化行為受到Ni2+的成分和溫度的影響較大。當Ni2+的物質的量分數不大于0.5時，Mn2+和Fe3+的占位有序化行為受到溫度影響較大，隨溫度升高，越來越多的Mn2+和Fe3+相互交換位置，占位有序化減弱；當Ni2+的物質的量分數大于0.5時，Mn2+其完全占據在8a亞晶格位置上，Fe3+完全占據在16d亞晶格位置，并且幾乎不隨溫度的變化而發生變化。

通過對比已有NixMn1-xFe2O4(x=0、0.25、0.5、0.75、1)中Ni2+、Mn2+以及Fe3+的占位有序化行為的文獻結果與本文在相同成分時的計算結果，發現兩者吻合得較好。證明了基于亞晶格模型，結合材料熱力學與第一性原理計算的方法對預測鎳錳鐵氧體中陽離子占位有序化行為具有較高的可靠性。由于Wei等[12]已經對NixMn1-xFe2O4(x=0、0.25、0.5、0.75、1)體系進行了系統研究，因此，本文研究了其他成分下NixMn1-xFe2O4(x=0.125、0.375、0.625、0.875)中Ni2+、Mn2+以及Fe3+的占位有序化行為，并預測了各個成分在1 523 K時的占位結構。文獻對這些成分的鎳錳鐵氧體研究的結果鮮有報道。因此，本文預測出的精細結構可以為相關材料設計提供重要的結構信息。

圖4　NixMn1-xFe2O4體系立方尖晶石中陽離子的占位分數隨熱處理溫度和成分的變化趨勢圖Fig.4 Cation occupying fraction dependence on heat treatment temperature and composition in cubic spinel NixMn1-xFe2O4

表3　NixMn1-xFe2O4體系中陽離子的占位結果Table 3 Site occupation of NixMn1-xFe2O4

3　結　論

本文基于熱力學亞晶格模型，將材料熱力學與第一性原理計算相結合，較為準確地預測了立方結構的尖晶石體系ZnxMn1-xFe2O4與NixMn1-xFe2O4中陽離子在亞晶格上的占位有序化行為隨溫度和成分的變化規律，得出結論如下：

(1)在ZnxMn1-xFe2O4中，室溫下Zn2+、Mn2+完全占據在8a亞晶格上，Fe3+完全占據在16d亞晶格上，屬于正尖晶石結構，且Zn2+比Mn2+更傾向于占據在8a亞晶格上；隨溫度的升高，Zn2+與Mn2+均會與Fe3+發生位置交換行為，與實驗結果吻合。本文也分析討論了不同成分下的陽離占位有序化行為。

(2)在NixMn1-xFe2O4中，Ni2+強烈地傾向于占據在16d亞晶格上，其占位幾乎不隨溫度和成分的變化而發生變化，Mn2+傾向于占據在8a亞晶格上，而Fe3+傾向于占據在16d亞晶格上，僅在溫度較高時發生部分位置交換，與實驗結果吻合。

(3)本文預測結果與可靠的文獻結果吻合較好，表明采用熱力學亞晶格模型，結合第一性原理計算和熱力學計算的方法可以應用于鐵氧體中陽離子的占位有序化行為預測，并且具有一定的普適性。

[1] Taghavaei A H, Shokrollahi H, Janghorban K. J. Magn. Magn. Mater., 2009,321:3926-3932

[2] Shokrollahi H. J. Magn. Magn. Mater., 2008,320:463-474

[3] Wang Y M, Wang X, Jiang Y F, et al. Rare Met., 2006,25: 531-535

[4] Sun Q C, Sims H, Mazumdar D, et al. Phys. Rev. B, 2012, 86:205106

[5] David S, Alberto R, Ricardo G, et al. Phys. Rev. B, 2015,91: 195106

[6] Huang J R, Cheng C. J. Appl. Phys., 2013,113:033912

[7] Zaag P J, Brabers V A M , Johnson M T, et al. Phys. Rev. B, 1995,51:12009

[8] Mathur P, Thakur A, Singh M. Phys. Scr., 2008,77:045701

[9] Wang J, Zeng C, Peng Z M, et al. Physica B, 2004,349:124-128

[10]Atsuto S, Koretaka Y, Fumiyasu O, et al. Phys. Rev. B, 2006, 73:184117

[11]Wei S H, Zhang S. Phys. Rev. B, 2001,63:045112

[12]Wei Q M, Li J B, Chen Y J, et al. Mater. Chem. Phys., 2002, 74:340-343

[13]Sickafus K E, Wills J M, Grimes N W. J. Am. Ceram. Soc., 1999,82:3279-3292

[14]Mats H. J. Alloys Compd., 2001,320:161-176

[15]Wu B, Zinkevich M, Aldinger F, et al. Intermetallics, 2008, 16:42-51

[16]Anubhav J, Geoffroy H, Shyue P O, et al. Phys. Rev. B, 2011,84:045115

[17]Stephan L. Phys. Rev. B, 2008,78:245207

[18]ZHANG Chao-Hui(張朝輝), ZHANG Li-Kun(張立昆), WU Bo(吳波), et al. (中國稀土學報), 2011,29:146-152

[19]Wu B, Zinkevich M, Aldinger F, et al. J. Solid State Chem., 2007,180:3280-3287

[20]Kresse G, Hafner J. J. Phys.: Condens. Matter., 1994,6:8245

[21]John P P, Kieron B, Matthias E. Phys. Rev. Lett., 1996,77: 3865

[22]Andersson J O, Thomas H, Lars H, et al. Calphad, 2002,26: 273-312

[23]Yuki M, Hikaru K, Shinji K, et al. Surf. Interface Anal., 2010,42:1655-1658

[24]Stefan P, Holger H, Marco S, et al. RSC Adv., 2013,3:23001 -23014

[25]Abbas T, Khan Y, Ahmad M, et al. Solid State Commun., 1992,82:701-703

[26]Attia S M. Egypt. J. Solids, 2006,4:e340

[27]O′neill H S C, Annersten H, Virgo D. Am. Mineral., 1992, 77:725-740

[28]Szotek Z, Temmerman W, K?dderitzsch D, et al. Phys. Rev. B, 2006,74:174431

[29]Henderson C M B, Charnock J M, Plant D A. J. Phys.: Condens. Matter., 2007,19:076214

[30]Fatemi D J, Harris V G, Browning V M , et al. J. Appl. Phys., 1998,83:6867-6869

[31]Dong H L, Hong S K, Chul H Y, et al. Mater. Chem. Phys., 1998,57:169-172

[32]Kumara A M, Raju T R K P, Rao P A, et al. Int. J. Adv. Sci. Res. Sc. Technol., 2012,1:1-4

[33]Miller A. J. Appl. Phys., 1959,30:S24-S25

Study of the Site Occupancy Ordering Behaviors of Cations in the AxMn1-xFe2O4Ferrites (A=Zn, Ni)

CHEN Zu-Hua1FANG Yuan1WU Bo＊,,1WU Yu-Feng1FAN Zhi-Yu1SA Bai-Sheng1ZHENG Fu-Nan2HUANG Jin-Tao2
(1College of Material Science and Technology, Fuzhou University, Fuzhou 350100, China)
(2TDK Xiamen Co., Ltd. Xiamen 361021, China)

Based on the crystal structure of spinel, we applied the thermodynamic ternary sublattices model to investigate the site occupancy ordering behaviors of Zn2+, Ni2+, Mn2+and Fe3+on the 8a and 16d sublattices in the ZnxMn1-xFe2O4and NixMn1-xFe2O4by combining thermodynamic calculations with first-principles calculations. Our results suggest that in the manganese ferrites, Mn2+occupies the 8a sublattice completely, and Fe3+occupies the 16d sublattice at room temperature, which belongs to a normal spinel. The site configuration is (Fe3+0.09Mn2+0.91) [Fe3+1.91Mn2+0.09]O4, when the ferrite is subjected to the heat treatment of 1 273 K. When the temperature increases to 1 473 K, the site configuration is (Fe3+0.11Mn2+0.89)[Fe3+1.89Mn2+0.11]O4, which agrees well with the available reliable experimental results. In the zinc ferrites, Zn2+occupies the 8a sublattice completely, and Fe3+completely occupies the 16d sublattice at room temperature. It also belongs to normal spinel, and the cations trend to exchange the site occupancy each other at higher temperature. In the Ni ferrites, all Ni2+occupies the 16d sublattice, and theFe3+cations occupy both the 8a and the 16d sublattices, which agrees with the experimental results. It belongs to an inverse spinel. Then, the relationship between the occupancy behaviors and the composition, as well as the heat treatment temperature in the ZnxMn1-xFe2O4and NixMn1-xFe2O4were established based on theoretically predictions.

spinel; Mn-Zn ferrites; ordering behavior; thermodynamic model; first-principles calculations

TB321

A

1001-4861(2016)03-0377-09

10.11862/CJIC.2016.026

2015-10-27。收修改稿日期：2015-11-12。

國家自然科學基金(No.50971043，51171046),教育部高等學校博士學科點專項科研基金(博導類)(No.20133514110006)，福建省自然科學基金(No.2014J01176)，TDK集團科技開發項目(No.T120-XM-001)資助。

＊通信聯系人。E-mail：wubo@fzu.edu.cn；會員登記號：E493110551S。