基于混沌優化蝙蝠算法的含分布式電源配電網故障區段定位

柳巖妮，公茂法，王來河，公　政

(1. 山東科技大學，山東青島266590； 2. 國網山東濰坊市供電公司，山東濰坊261000)

?

基于混沌優化蝙蝠算法的含分布式電源配電網故障區段定位

柳巖妮1，公茂法1，王來河1，公政2

(1. 山東科技大學，山東青島266590； 2. 國網山東濰坊市供電公司，山東濰坊261000)

針對含分布式電源配電網故障區段定位問題，改進了已有的開關函數，并提出了一種基于混沌優化蝙蝠算法的診斷方法。利用蝙蝠算法全局尋優能力對配電網故障區段進行定位搜索，并針對蝙蝠算法易陷入局部最優的缺點，使用混沌策略對部分最優個體進行優化，使其收斂速度加快，定位準確度提高。通過建立算例配電網模型，對其多種故障定位結果分析表明，算法對于含分布式電源配電網故障區段定位具有一定的實用性。

分布式電源；配電網；故障區段定位；蝙蝠算法；混沌優化

0　引言

隨著電力行業的不斷發展與完善，分布式電源開始被應用到配電網中，配電網由之前的單電源形式開始轉變為多電源輻射結構，由此為配電網故障診斷帶來了一定的問題。常見的用于配電網故障診斷的人工智能算法有遺傳算法[1]、Petri網[2]、神經網絡[3]等，這些智能算法在故障診斷方面的準確率較高且具有一定的容錯性，但是在實際的應用中建模復雜，往往需要大量的數據，且效率不高。另外的一種方法就是圖論算法，主要以矩陣算法[4-5]為主，該算法計算效率較高，但是當饋線終端單元上傳的信息發生錯誤或者丟失的情況時，往往準確率較低。針對上述不足之處，該研究提出了一種基于混沌優化蝙蝠算法的方法對含分布式電源配電網故障進行診斷。

蝙蝠算法是一種新型仿生智能算法，主要模擬了蝙蝠搜索獵物的過程，與已提出的仿生算法相比，蝙蝠算法具有所需參數少、收斂速度快等優點，但其也存在易陷入局部最優且尋優精度不高的問題。本文使用了混沌算法對部分精英個體進行混沌優化，從而使算法避免無效迭代，達到更好的尋優精度。將該算法用于含分布式電源配電網的故障區間定位，并進行實例分析，結果表明該算法具有全局收斂能力較強、尋優精度高等優點，對需利用復雜函數優化的工程問題有著一定的適用性和實用性。

1　蝙蝠算法基本原理

1.1蝙蝠算法

蝙蝠算法[6-7]是模擬微型蝙蝠的回聲定位原理形成的一種新的智能算法。其主要原理是隨機分布的蝙蝠通過不同的脈沖速率來搜尋獵物，其初始的脈沖速率較小，脈沖音強較大，當搜尋到獵物后會增大脈沖速率并適當減小脈沖音強。然后將現在的位置狀態與最優的位置比較，如果仍然處于劣勢位置則移動位置，再繼續搜索，直到所有的蝙蝠個體都處在靠近獵物的位置，即最優位置。

蝙蝠在搜尋獵物的過程中脈沖頻率、速度和位置的更新公式如式(1)所示。

(1)

式中：d表示蝙蝠群體的搜索空間維數；α為[0,1]均勻分布的隨機變量；fmin，fmax分別表示脈沖頻率的最小值和最大值；fi表示第i只蝙蝠搜索獵物時所發出的脈沖速率；X*為當前蝙蝠群體的最優位置；Vi(t+1)，Vi(t)，Xi(t+1)，Xi(t)分別表示第i只蝙蝠在t+1和t時刻的速度和位置狀態值。

蝙蝠群體在搜索過程中，如果鎖定了獵物就需要將脈沖音強減小，脈沖速率增加，從而更容易定位獵物所在位置，其發射脈沖速率和音強更新公式如式(2)所示。

(2)

式中：β和γ分別為脈沖音強衰減系數和脈沖速率增加系數；Ai(t+1)，Ai(t)分別為t+1和t時刻的脈沖音強；ri(t+1)表示蝙蝠在t+1時刻的脈沖速率；ri0為最大脈沖速率。

1.2基于混沌優化的蝙蝠算法

由于蝙蝠算法迭代后期容易陷入局部最優，且種群多樣性減少，本文采用混沌算法對前n%個精英個體的位置和速度進行混沌優化，并將其映射到原解空間范圍內，使其種群個體多樣性增加，跳出局部最優繼續迭代搜索。

混沌算法是一種具有遍歷性、初值敏感性和隨機性的算法，其主要思想是將種群進行混沌優化，再將優化序列值映射到混沌模型原解所在的空間范圍內。本文采用一維非線性映射模型Logistic映射[8]對蝙蝠種群進行混沌優化，其公式如式(3)所示。

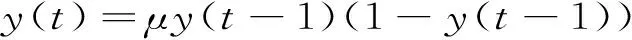
(3)

式中：μ是控制變量，本文取μ=4。

將得到的混沌序列通過式(4)映射到原解空間內。

(4)

基于混沌優化蝙蝠算法具體的實現步驟如下[9]：

(1)參數初始化。空間維數為d，聲波頻率范圍為[fmin，fmax]，最大聲波發射速率為r0，最小聲波強度為A0，聲波強度衰減系數為β，聲波發射速率增加系數為γ，適應度最小值連續出現次數K，最大迭代次數為g。

(2)初始化種群。計算種群個體的適應度值找到種群當前最佳位置X*。

(3)初始化搜索脈沖頻率fi，并根據式(1)更新蝙蝠個體的空間位置和速度。

(4)產生隨機的rand1,若rand1>ri，則對處于最優位置的蝙蝠進行隨機擾動，用擾動后的位置代替當前位置。

(5)產生隨機的rand2，若rand2>Ai，且蝙蝠所處位置得到了優化，個體則移動到更新后的位置。

(6)如果步驟(5)條件得到滿足，則根據式(2)更新脈沖速率r和脈沖音強A，否則，跳轉到步驟(7)。

(7)計算當前群體的適應度值，并對前n%最優個體按照式(3)進行位置和速度的混沌優化，然后將得到的混沌序列映射到原解空間，判斷如果迭代次數達到最大值或者適應度值出現次數大于設定值，則跳轉到步驟(8)，否則轉到步驟(2)繼續搜索尋優。

(8)輸出最優個體的值和全局極值點，算法結束。

2　含分布式電源配電網故障區段定位模型

配電網發生故障后，每個區段上的FTU檢測到故障電流后，如果超過整定值后則會上傳到SCADA主站系統，故障定位算法會根據接收的信息計算并定位故障區段。基于混沌優化蝙蝠算法的故障定位方法主要是通過適應度函數和開關函數進行分析的，具體構建方案如下。

2.1開關函數的建立

對配電網進行故障區間定位需要將FTU上傳的分段開關的電流信息轉化為線路的故障狀態值，將故障電流與故障狀態之間的關系定義為開關函數。含分布式電源的配電網在進行故障區間定位時，傳統的算法往往需要多次設定電流方向，且不考慮分布式電源投切問題，使得故障定位的準確率受到一定影響。本文對已有的開關函數[10-11]進行了改進，定義了一種新的開關函數如式(5)所示。

(5)

將以i個開關為中心靠近系統電源的區域定義為配電網系統的上半區，靠近分布式電源的部分定義為下半區。其中，“∏”表示邏輯或，Ksi，Kj分別為上半區和下半區的電源開關系數，表示對應的區域電源是否接入，如果接入則對應的開關系數取值為1，否則為0；xs1，xs2分別表示第i個開關的上下半區包含的饋線區段狀態值，發生故障時取1，否則為0；S1，S2分別為第i個開關上下半區包含的饋線區段總數目。

2.2適應度函數的建立

適應度函數是用來評價所用算法取得最優解的情況，其結果反映了期望故障情況與實際情況的偏離程度，主要是根據FTU上傳到主站的狀態值以及假設故障情況求得各個區段的期望狀態值。針對含分布式電源配電網故障區間定位問題，構建了如式(6)所示的適應度函數。

(6)

3　算例分析

本文對圖1所示的含分布式電源的配電網進行故障區段定位分析。其中，S為系統電源，1～17為分段開關，L1～L17為饋線區段，K1～K3為分布式電源DG1～DG3接入配電網的開關，若分布式電源接入配電網則對應的開關Kj(j=1,2,3)取值為1，否則為0。

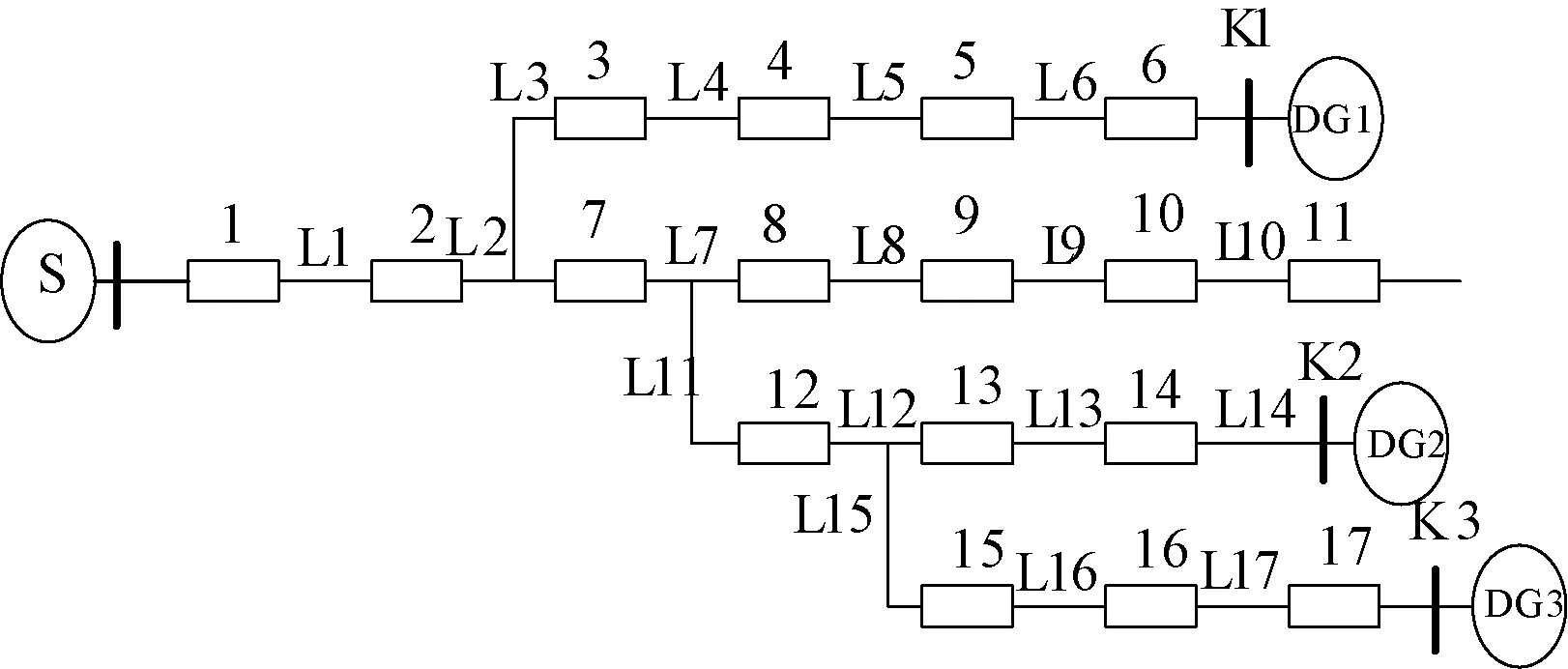
圖1　含分布式電源的算例配電網結構

利用Matlab對算法進行編程，其中的相關參數設定：種群搜索空間維數為17，聲波頻率最小值取0，最大值取2，蝙蝠脈沖速率和脈沖音強初始值均取作0.25，適應度值最小值連續出現次數K=20，最大迭代次數設定為300。

利用本文所提出的故障定位算法對算例配電網進行了多種不同情況下的故障區段定位仿真，以驗證該算法的可靠性和容錯性。下面對FTU上傳信息未發生畸變和發生畸變兩種情況進行分析，并又將上述兩種情況分為接入分布式電源和未接入分布式電源兩種形式進行故障定位，具體的故障定位仿真結果如表1、表2所示。

表1　無畸變信息的故障定位仿真結果

表2　發生畸變的故障定位仿真結果

由表1可以看出，在FTU上傳的電流狀態信息未發生畸變的情況下，能準確地定位接入分布式電源或者未接入分布式電源的配電網單重和多重故障區段。從表2 可以看出，當電流信息狀態值發生畸變時，也可以很準確地對多種情況的故障區段進行定位。故障定位結果分析表明，本文方法具有一定的容錯性和可靠性，能夠實現對配電網多種故障形式進行準確定位。

為驗證CBA算法的有效性，本文還采用了BA，PSO，GA算法對上述模型進行了仿真測試，并使用平均迭代次數和平均陷入局部最優的次數作為檢驗的標準進行對比，對比結果如表3所示。結果表明，基于混沌優化的蝙蝠算法，由于引入了混沌優化策略，其性能明顯得到提高，比BA，PSO，GA算法收斂速度更快，且不易陷入局部極值，可以得到較好的故障定位效果。

表3　算法仿真結果比較

4　結論

本文提出了一種基于混沌優化蝙蝠算法的含分布式電源配電網故障區段定位方法。算法采用了混沌策略對部分最優個體進行了混沌優化，使搜索后期種群多樣性增加，并跳出局部最優的限制。同時，對含分布式電源的配電網開關函數進行了改進，使其更加適應分布式電源接入配電網的故障區段定位。定位結果和對比結果表明，基于混沌優化蝙蝠算法的配電網故障區段定位方法具有很好定位效果，并具有一定的容錯性。

[1]王進強,陳少華.基于改進遺傳算法的含分布式電源的配電網故障定位[J].電力科學與工程, 2013, 29(12): 13 -17.

[2]呂航.Petri網和冗余糾錯技術結合的配電網故障區段定位新方法[J].中國電機工程學報,2004,24(10):61-67.

[3]劉文軒,嚴鳳,田霖,等.基于LVQ神經網絡的配電網故障定位方法[J].電力系統保護與控制, 2012, 40 (5): 90-95.

[4]黃佳樂,楊冠魯.配電網故障區間定位的改進矩陣算法[J].電力系統保護與控制,2014,42(11):41-45.

[5]王進強,陳少華,尹雁和,等.含分布式電源的配電網故障區間定位算法[J].電力科學與工程,2011,27(2):25-29.

[6]劉長平,葉春明.具有混沌搜索策略的蝙蝠優化算法及性能仿真[J].系統仿真學報, 2013, 25 (6): 1183-1188.

[7]付家才,陸青松.基于蝙蝠算法的配電網故障區間定位[J].電力系統保護與控制, 2015, 43 (16):100-105.

[8]朱紅求, 陽春華，桂衛華，等. 一種帶混沌變異的粒子群優化算法[J].計算機科學, 2010, 37(3): 215- 217.

[9]馬迎東,王文棟,溫強.基于混沌搜索策略蝙蝠算法的輸電網規劃[J].電力系統保護與控制,2015,43(15):17-21.

[10]周湶,鄭柏林,廖瑞金,等.基于粒子群和差分進化算法的含分布式電源配電網故障區段定位[J].電力系統保護與控制,2013,41(4):33-37.

[11]劉鵬程,李新利.基于多種群遺傳算法的含分布式電源的配電網故障區段定位算法[J].電力系統保護與控制,2016,44(2):36-41.

Fault Location of Distribution Network with Distributed Generation Based on Chaos Optimization Algorithm

LIU Yanni1, GONG Maofa1, WANG Laihe1, GONG Zheng2

(1. Shandong University of Science and Technology, Qingdao 266590, China;2. State Grid Shandong Weifang Electric Power Company, Weifang 261000, China)

Aiming at the fault section location problem for the distribution network with distributed generation, this paper improves the existing switching function, and furthermore, puts forward a new method based on chaos optimization. The global searching ability of the bat algorithm is applied to the distribution network for searching and positioning of the fault section, in the light of the weak point of bat algorithm, which is easy to fall into local optimum, chaos strategy on the part of the best individual optimization is used. So the convergence speed accelerates with its positioning accuracy improved as well. By setting up a distribution network model of an instance, some analysis is launched, and the results show that the algorithm can be applied to the fault section location of distribution network with distributed generation and is relatively practical.

distributed generation; distribution network; fault section location; bat algorithm; chaos optimization

2016-05-31。

山東省自然科學基金(ZR2012EEM021)。

柳巖妮(1991-)，女，碩士研究生，主要從事電力系統自動化的研究，E-mail：yanniliu99@163.com。

TM711

A

10.3969/j.issn.1672-0792.2016.08.003